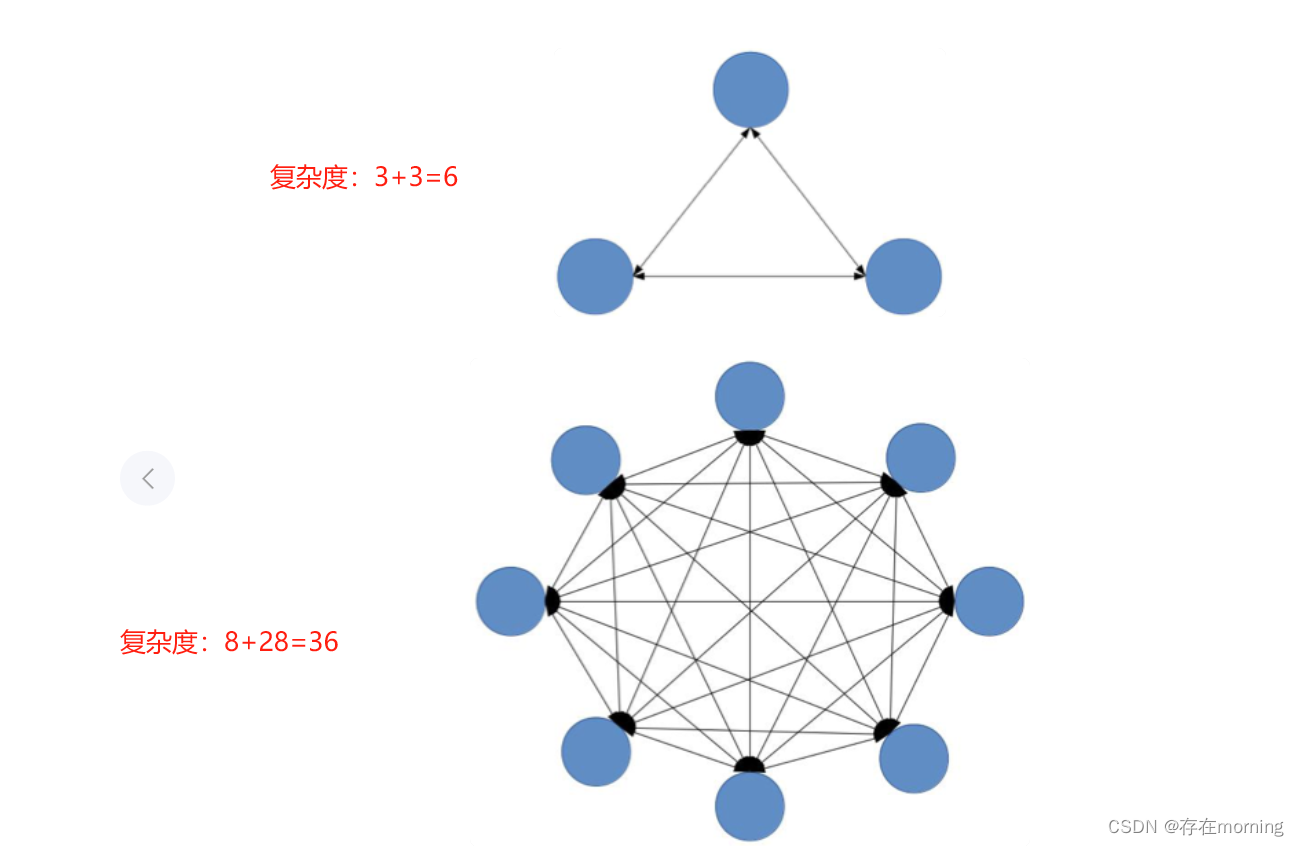
信号处理领域学者为了改进小波变换在各时频区间能量聚集性不高的缺点,有学者在小波分析基础上引入调频算子构成了线性调频小波变换,线调频小波一方面继承了小波变换的理论完善性,另一方面用一个新的参数(线调频参数)刻画信号短时频率变化特征。
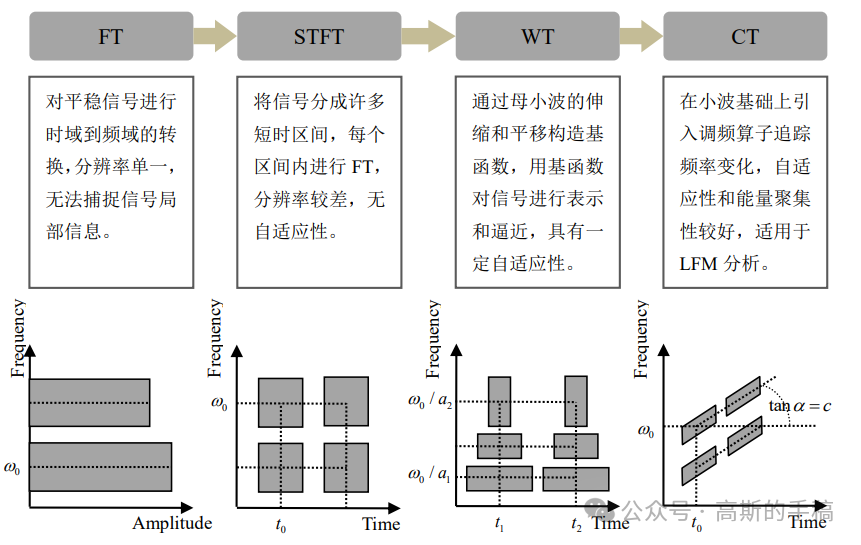
传统的傅里叶变换只能分析平稳信号,将时域信号转到频域进行分析,是一种纯频域分析(即时间分辨率为零);短时傅里叶变换通过引入窗函数,对于非平稳信号,能进行时域和频域中的局部分析,但窗函数固定导致时频分析网格固定(即时频分辨率固定);小波变换通过对母小波伸缩形成一族基函数,时频分析网络不但能随时间平移还能根据时间和频率轴的比例尺度进行改变,形成长宽大小不一的长方形时频分析网格,适用性更强;线调频小波变换在小波基函数中引入调频算子使时频分析网格旋转与时间轴形成夹角,从而具有在短区间内追踪频率变化的能力,尤其适合分析线调频信号。从信号处理的维度来看,线调频小波可以看成更广义的小波,傅里叶基只用频移一个参数刻画信号,短时傅里叶基和小波基用频移、时移两个参数刻画信号,而线调频小波基用频移、时移、频变三个参数刻画信号。实际问题中的非平稳振动信号常可以看成调幅调频的信号,EMD、LMD、VMD 等分解中均涉及到将分解后信号看成调幅调频信号,只是关于信号频率的变化都用一个抽象的相位函数进行表示,实际上对于一个任意频率时变的信号,在短时间内其频率变化确是可以用线性变化进行拟合,这个频率线变的短时区间与小波分析的时窗区间相比宽度明显要长些,因此可以将线调频小波的分析区间为短时线变区间,小波的分析区间称为短时区间。
从以上分析不难看出,如果将线调频小波应用到时变系统响应分析中,一方面可以提高时频分析时的能量聚集性,提高瞬时频率的追踪性和识别精度。另一方面,线调频小波与动力学方程结合时,由于分析区间为短时线变区间,可以基于频率线变假设而非传统的时不变假设构造识别方法,这样明显拓宽了分析区间长度,从而降低计算所需步长数目,这对于提高识别算法的效率将大有裨益。此外,由于线调频小波基函数的构造具有完善的理论基础,将线调频小波与动力学方程结合时可以探究基于线调频信号的相关性分析。
% component A
dt_a = 46; % even please, length of component A
tc_a = 90; % time-center of component A
fc_a = 1/dt_a; % frequency-center of A
s_a = -sin(2*pi*fc_a*(0:dt_a-1)/fs); % signal A
% component B, use the same as component A
tc_b = 422;
s_b1 = -(1/2 * sawtooth(2*pi*2*fc_a*(0:dt_a/2-1)/fs, 1/2) + 1/2);
s_b2 = -s_b1;
s_b = [s_b1,s_b2]; % signal B
% component C
dt_c = 28; % length of C
fc_c = 0.4; % frequency center of C
tc_c = 256; % time center of C
s_c = gabor1d(T, fs, dt_c, fc_c, tc_c, 1, 0); % signal C
% construct Wave I
waveI(round(tc_a-dt_a/2):round(tc_a-dt_a/2)+dt_a-1) = s_a;
waveI(round(tc_b-dt_a/2):round(tc_b-dt_a/2)+dt_a-1) = s_b;
waveI = waveI + s_c;
%%
% * Wave II is a Gabor waveform (D).
dt_d = 2 * dt_c; % length of D
fc_d = 2 * fc_c / 3; % frequency center of D
tc_d = 256; % time center of D
s_d = gabor1d(T, fs, dt_d, fc_d, tc_d, 1, 0);
waveII = s_d;
%%
% * Wave III consists of a pulse (E) and a sinusoidal (F) waveform.
tc_e = 128; % component E
s_e = gabor1d(T, fs, 0, 0, tc_e, 2, 0); % the pulse
fc_f = .35; % component F
A_f = .2;
s_f = A_f * sin(2*pi*fc_f * (0:T*fs-1)/fs);
% construct Wave III
知乎学术咨询:
https://www.zhihu.com/consult/people/792359672131756032?isMe=1
waveIII = s_e + s_f;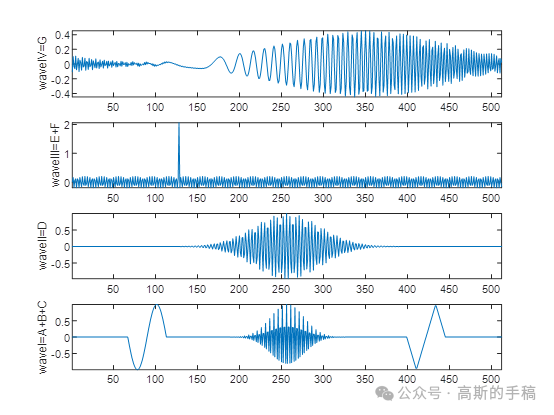
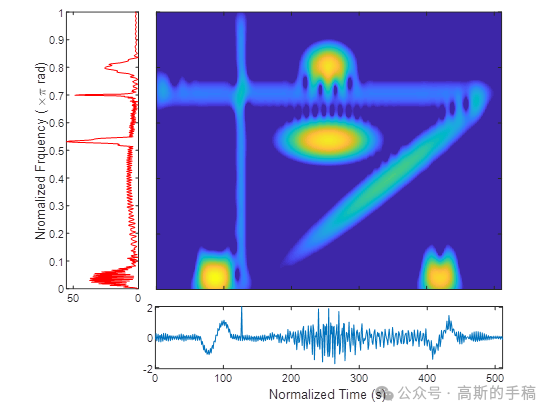
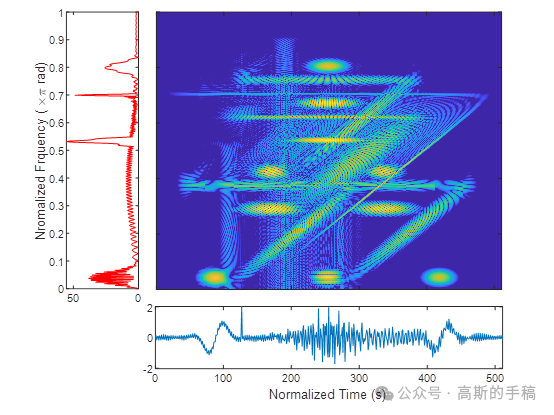
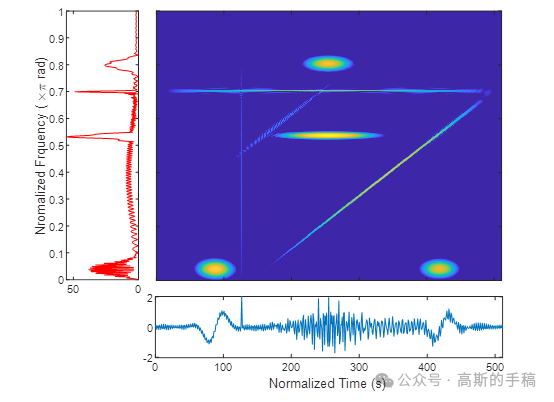
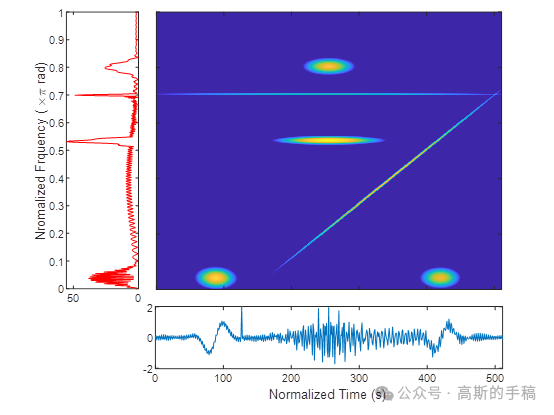
- 工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。