LeetCode-Leetcode 1120:子树的最大平均值
- 题目描述:
- 解题思路一:递归
- 解题思路二:0
- 解题思路三:0
题目描述:
给你一棵二叉树的根节点 root,找出这棵树的 每一棵 子树的 平均值 中的 最大 值。
子树是树中的任意节点和它的所有后代构成的集合。
树的平均值是树中节点值的总和除以节点数。
示例:
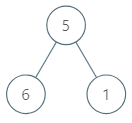
输入:[5,6,1]
输出:6.00000
解释:
以 value = 5 的节点作为子树的根节点,得到的平均值为 (5 + 6 + 1) / 3 = 4。
以 value = 6 的节点作为子树的根节点,得到的平均值为 6 / 1 = 6。
以 value = 1 的节点作为子树的根节点,得到的平均值为 1 / 1 = 1。
所以答案取最大值 6。
提示:
树中的节点数介于 1 到 5000之间。
每个节点的值介于 0 到 100000 之间。
如果结果与标准答案的误差不超过 10^-5,那么该结果将被视为正确答案。
解题思路一:递归
算法思路:
用一个二维数组表示子树的所有节点的和与节点数量。
空节点返回0,0
非空节点返回,左子树和与右子树和与当前值的总和,左右子树总个数+1
更新res
class Solution:
def maximumAverageSubtree(self, root: TreeNode) -> float:
res = 0.0
def dfs(root):
nonlocal res
if not root:
return 0, 0
l, r = dfs(root.left), dfs(root.right)
values, nodes = l[0] + r[0] + root.val, l[1] + r[1] + 1
res = max(res, values/nodes)
return values, nodes
dfs(root)
return res
时间复杂度:O(n)
空间复杂度:O(logn)
解题思路二:0
时间复杂度:O(n)
空间复杂度:O(n)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)



♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠