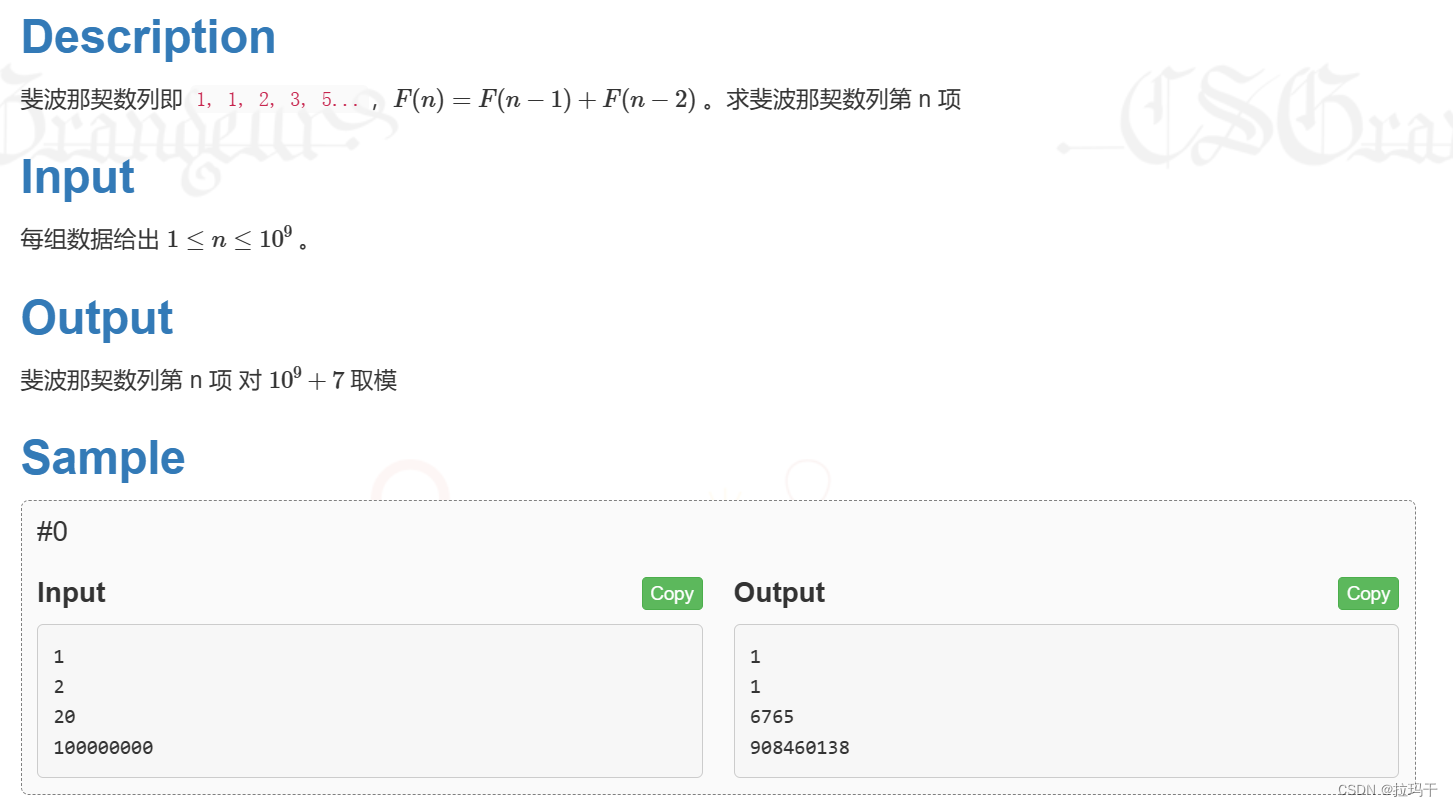
Description

斐波那契数列即 1, 1, 2, 3, 5...，�(�)=�(�−1)+�(�−2) 。求斐波那契数列第 n 项

Input

每组数据给出 1≤�≤109 。

Output

斐波那契数列第 n 项 对 109+7 取模

Sample

#0

Input

Copy

1
2
20
100000000

Output

Copy

1
1
6765
908460138

代码有点丑陋，思路就是矩阵快速幂

#include <iostream>
using namespace std;
#include <cmath>
long long mod = 1e9 + 7;
long long quickPow(long long n, long long mod)
{
    long long a[4][4], now[4][4];
    a[1][1] = 1;
    a[1][2] = 0;
    a[2][1] = 0;
    a[2][2] = 1;

    now[1][1] = 0;
    now[1][2] = 1;
    now[2][1] = 1;
    now[2][2] = 1;

    long long temp[4][4];

    while (n > 0)
    {

        // cout << now[1][1] << " " << now[1][2] << endl;
        // cout << now[2][1] << " " << now[2][2] << endl;
        if (n % 2 == 1)
        {
            // a=a*now
            temp[1][1] = a[1][1];
            temp[1][2] = a[1][2];
            temp[2][1] = a[2][1];
            temp[2][2] = a[2][2];

            a[1][1] = ((temp[1][1] * now[1][1]) % mod + (temp[1][2] * now[2][1]) % mod) % mod;
            a[1][2] = ((temp[1][1] * now[1][2]) % mod + (temp[1][2] * now[2][2]) % mod) % mod;
            a[2][1] = ((temp[2][1] * now[1][1]) % mod + (temp[2][2] * now[2][1]) % mod) % mod;
            a[2][2] = ((temp[2][1] * now[1][2]) % mod + (temp[2][2] * now[2][2]) % mod) % mod;

            // cout << a[1][1] << " " << a[1][2] << endl;
            // cout << a[2][1] << " " << a[2][2] << endl;
        }
        // now=now*now
        temp[1][1] = now[1][1];
        temp[1][2] = now[1][2];
        temp[2][1] = now[2][1];
        temp[2][2] = now[2][2];

        now[1][1] = ((temp[1][1] * temp[1][1]) % mod + (temp[1][2] * temp[2][1]) % mod) % mod;
        now[1][2] = ((temp[1][1] * temp[1][2]) % mod + (temp[1][2] * temp[2][2]) % mod) % mod;
        now[2][1] = ((temp[2][1] * temp[1][1]) % mod + (temp[2][2] * temp[2][1]) % mod) % mod;
        now[2][2] = ((temp[2][1] * temp[1][2]) % mod + (temp[2][2] * temp[2][2]) % mod) % mod;
        n >>= 1;
    }
    return a[2][2];
}
int main()
{
    long long n;
    while (cin >> n)
    {
        cout << quickPow(n - 1, mod) << endl;
    }
    return 0;
}