学习目标：

重温高数知识，回顾导数、微分、偏导数‘全微分、方向导数、梯度；斜率、切线、切平面，法相平面、法线的知识’

• 函数微分与导数的含义
• 多元函数偏导数、全微分
• 函数式自动微分应用实践

昇思大模型 ，mindspore AI框架 学习记录：

---

一、函数微分与导数的含义

1.1 一元函数的导数和微分

导数是一个函数在某一点的斜率，它描述了函数在该点的变化率。具体来说，对于函数y=f (x)，如果在某一点x0处有增量Δx，那么增量之商Δy/Δx的极限值就是该点的导数，记作f’ (x0)。 而微分则是一种处理函数的方法，它表示函数在某一点处的变化量。

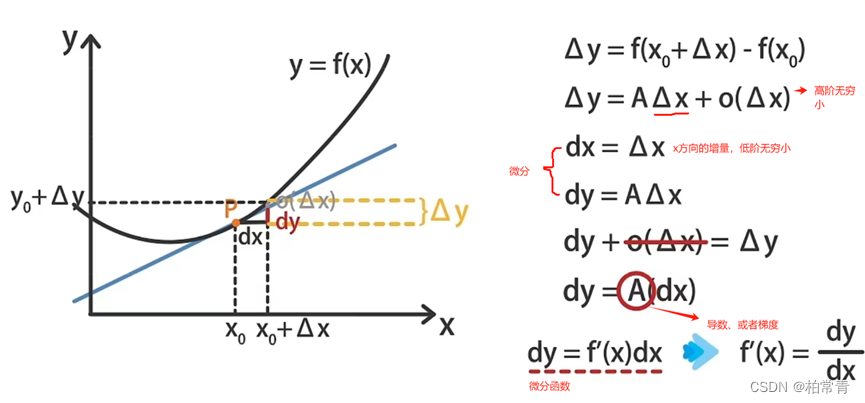
因此，导数是A，是数值；微分dy = Adx,是表示切线。
在该点（x0,y0）,如果A>0,曲线递增，A<0曲线递减，A=0，曲线平稳。
偏导数，全导数，方向导数，偏微分，全微分，梯度更多详情参考：博客。

二、多元函数偏导数、全微分

导数本质是一种极限，实际场景中表示切线斜率；
微分本质是“以直代曲，线性逼近”，让本来对曲线进行运算的操作，转化成对直线进行操作，简化了难度。
同理，对于多元函数，

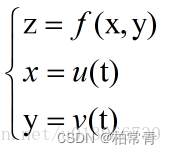
就有偏导数和偏微分。
偏导数仍然是增量的比值，只不过需要固定在某方向上算。


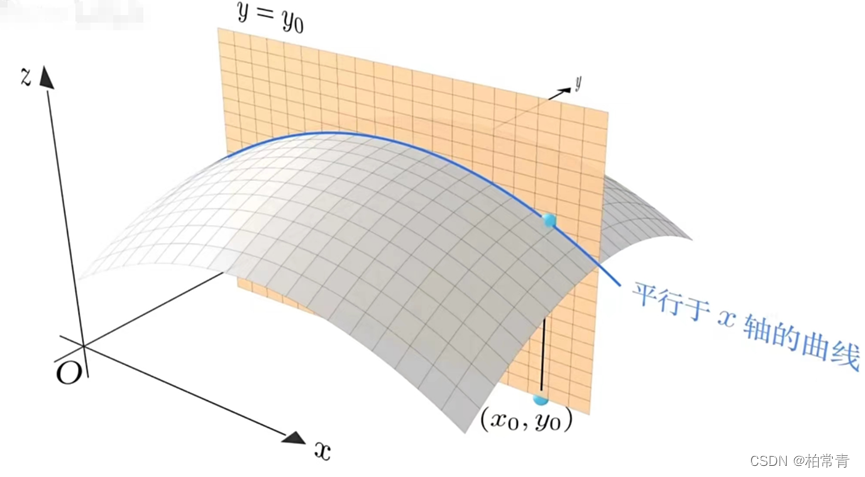
转到xoz平面来看：

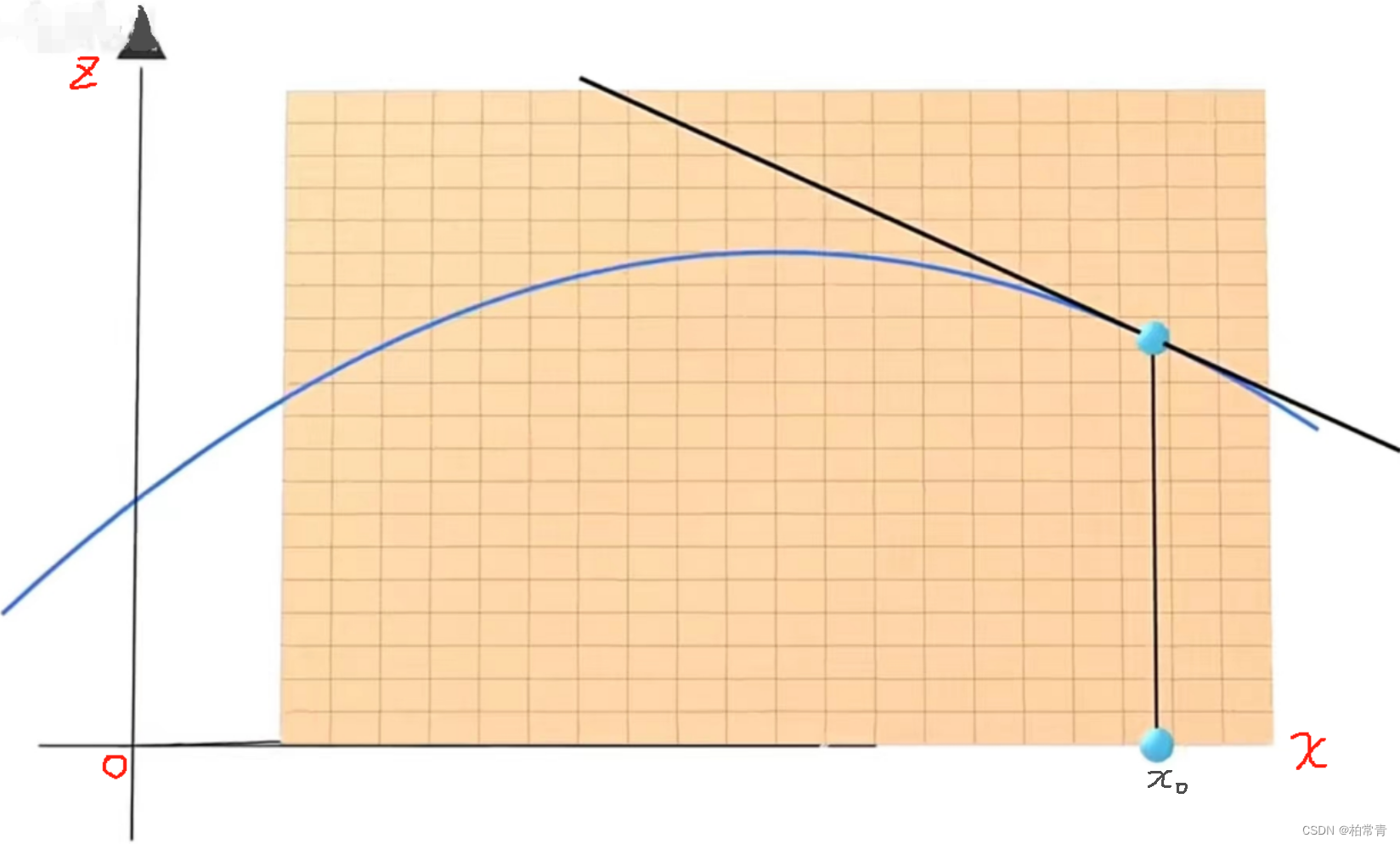
曲面在（x0,y0）上关于x的偏导数：

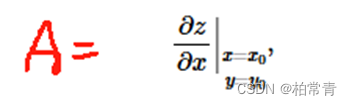
偏导数还有一种写法：

先看对曲面在固定y0面,对x的偏导数A：在该点A>0,曲面沿x轴递增，A<0曲面沿x轴递减，A=0，曲面沿x轴变化平稳。

这个偏导数在该点（x0,y0）计算出的导数（斜率）数值，结合x方向构成的向量就是该点在x方向的梯度。
重要概念：梯度是向量，有大小，有方向。

图上表示，箭头的长度就是向量的模（就是A），方向就是梯度变化的方向i(也就是x方向)。

同理，在固定x=x0时，z对y的偏导数为：
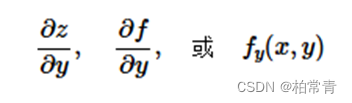同时，x=x0,y=y0,该点z对y的偏导数值B结合方向j，也就是y轴方向，构成了曲面在该点沿y轴的变化梯度。

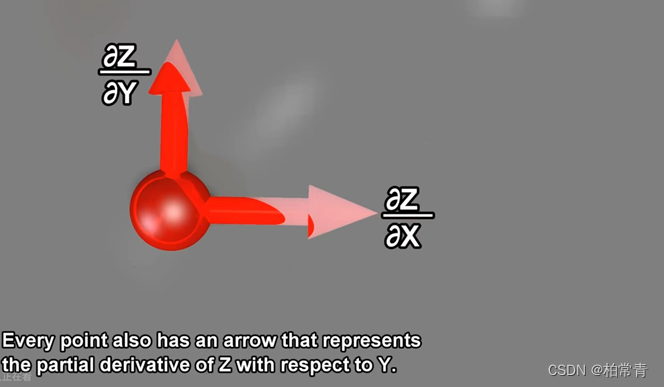
那么，曲面z在该点的总的方向梯度(总的方向导数)就是。向量合成（Ai,Bj）。

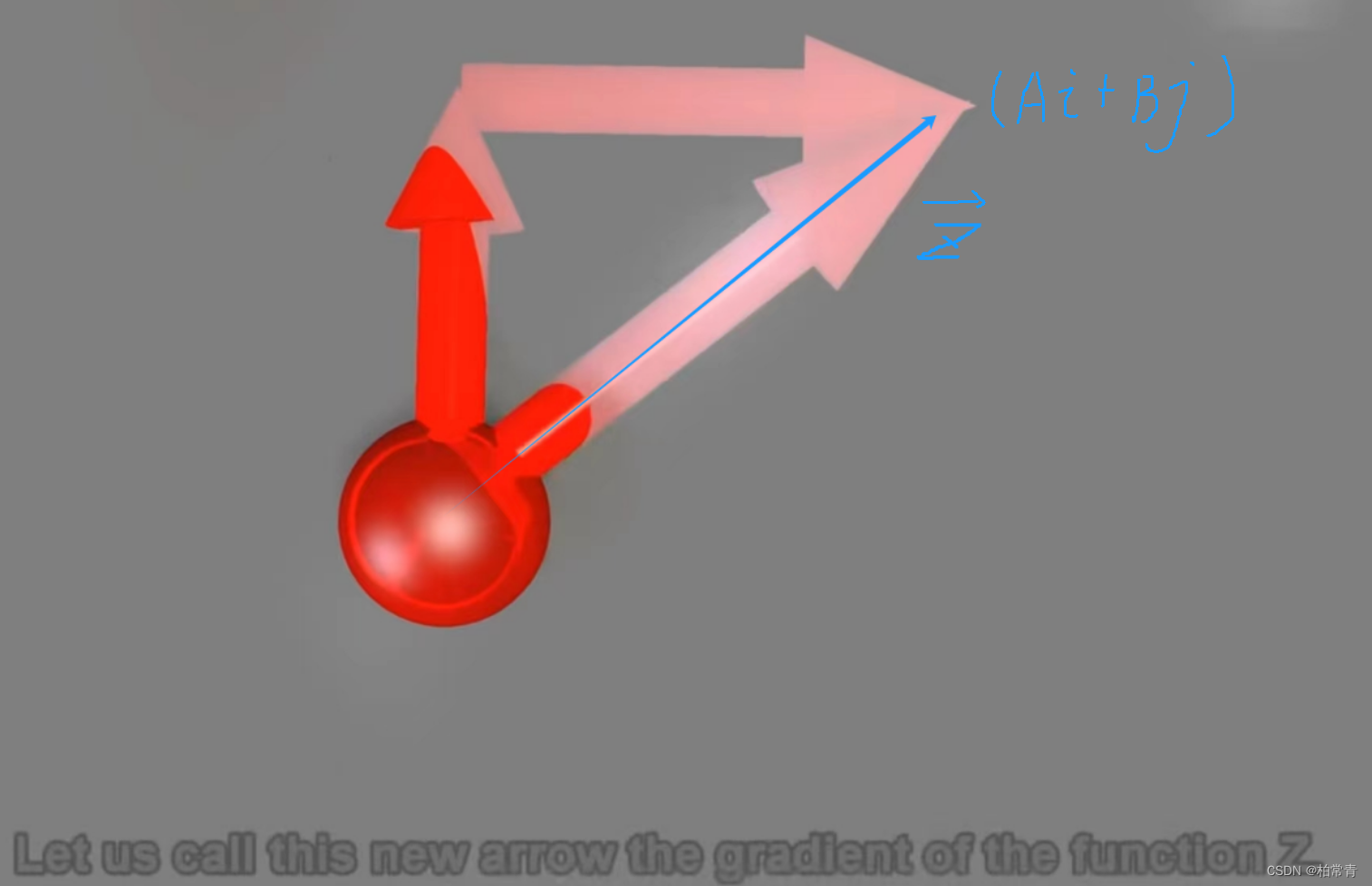
合成的这个方向导数，也就是梯度。就是曲面在该点的变化情况。
专业表达式如下：gradf(x0,y0) = df/dx|(x0,y0)i+df/dy|(x0,y0)

---

三、函数式自动微分应用实践

那么，问题来了，以上方向梯度对我们的AI模型或者说建模有什么意义呢。

3.1 多元函数梯度应用关联性

假如我们有一批数据X=[x1,x2,x3,x4]，知道这批数据表示的是Y=[y1,y2,y3,y4],为真实值。X->Y存在某种规律w0在里面。不过，我们不清楚这个w0。又有一批数据[x11,x12,x13,x14],能不能推出这批数据表示什么？
所以，我们需要解方程。

我们想要获得的某种规律w=[参数，......]，黑匣子w。它能让我们实现wX+b无限接近于Y。
Y_ = wx+b 为预测值
构造损失函数：L = F(x,y) =|wx+b - y|=|Y_-Y| 趋向于0.预测结果与真实结果的差值就是损失函数（其他方式计算损失函数类似，L >=0）。
你会发现，L(x,y)就是前面的多元函数，L(x,y)趋近于0，已知X,Y，去解关于w,b的方程。

3.2 函数代码实现梯度计算

import numpy as np
import mindspore
from mindspore import nn
from mindspore import ops
from mindspore import Tensor, Parameter

给定X,Y,然后初始化w,b为可变参数变量类型Parameter，通过计算曲线（曲平面）的梯度，来调整w,b。

x = Tensor([1,2,3,4,5],mindspore.float32)
y = Tensor([9,14,19,24,29],mindspore.float32)  # expected output
w = Parameter(Tensor(np.random.randn(5, 5), mindspore.float32), name='w') # weight
b = Parameter(Tensor(np.random.randn(5,), mindspore.float32), name='b') # bias
print(x,y,w,b)

为什么需要向梯度下降的方向来调整w,b。梯度下降表示函数值在减小，因为损失函数L(x,y)>=0，当函数值减小趋近于0，表示预测值和真实值趋于相同。从而达到模型参数的理想结果。

def function(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss

用fn表示梯度函数，这里是损失函数关于w和b的偏导数组成的偏导数。

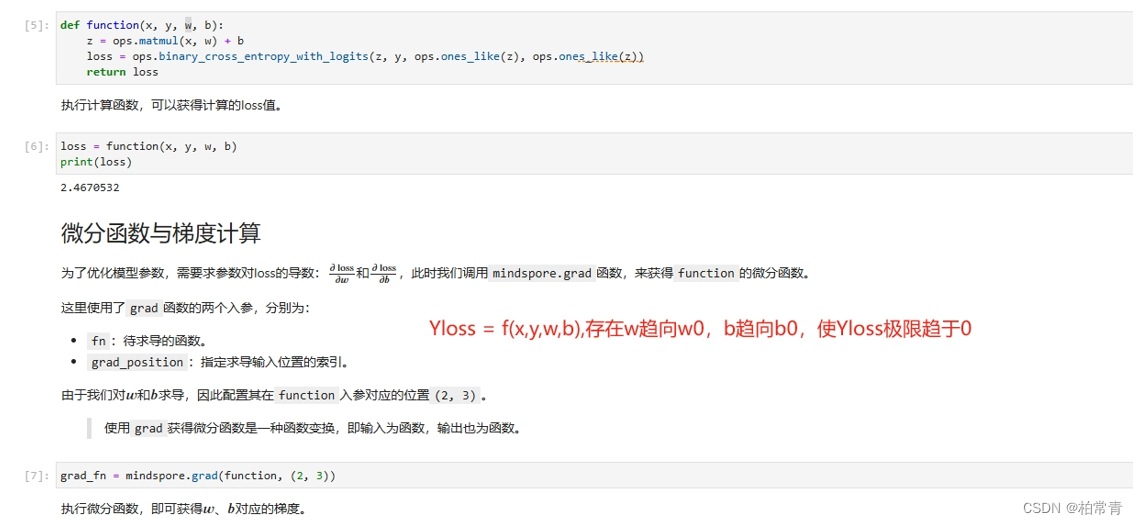
grad_fn = mindspore.grad(function, (2, 3))，此处索引 (2, 3)表示（w,b）。表示函数function对w,b求导数。参数索引一次x,y,,w,b索引=0,1,2,3。

3.2 梯度下降：随机梯度函数SDG

梯度在具体的模型训练时，会更具优化器来优化参数。
优化器作用过程：调整模型参数以减少模型误差的过程。MindSpore提供多种优化算法的实现，称之为优化器（Optimizer）。优化器内部定义了模型的参数优化过程（即梯度如何更新至模型参数），所有优化逻辑都封装在优化器对象中。在这里，我们使用SGD（Stochastic Gradient Descent）优化器。
深度学习模型多采用批量随机梯度下降算法进行优化，随机梯度下降（SGD）算法的原理如下：

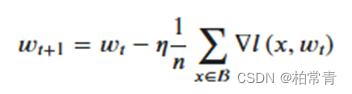
optimizer = nn.SGD(model.trainable_params(), learning_rate=learning_rate)

每输入一批X，计算一个Y。
按梯度下降方向，修改一次模型参数。

optimizer(grads)

3.3允许梯度和停止梯度计算

当损失函数返回除损失值外，还有其他中间结果时。直接计算函数梯度，会将loss和z的一起计算。

def function_with_logits(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss, z

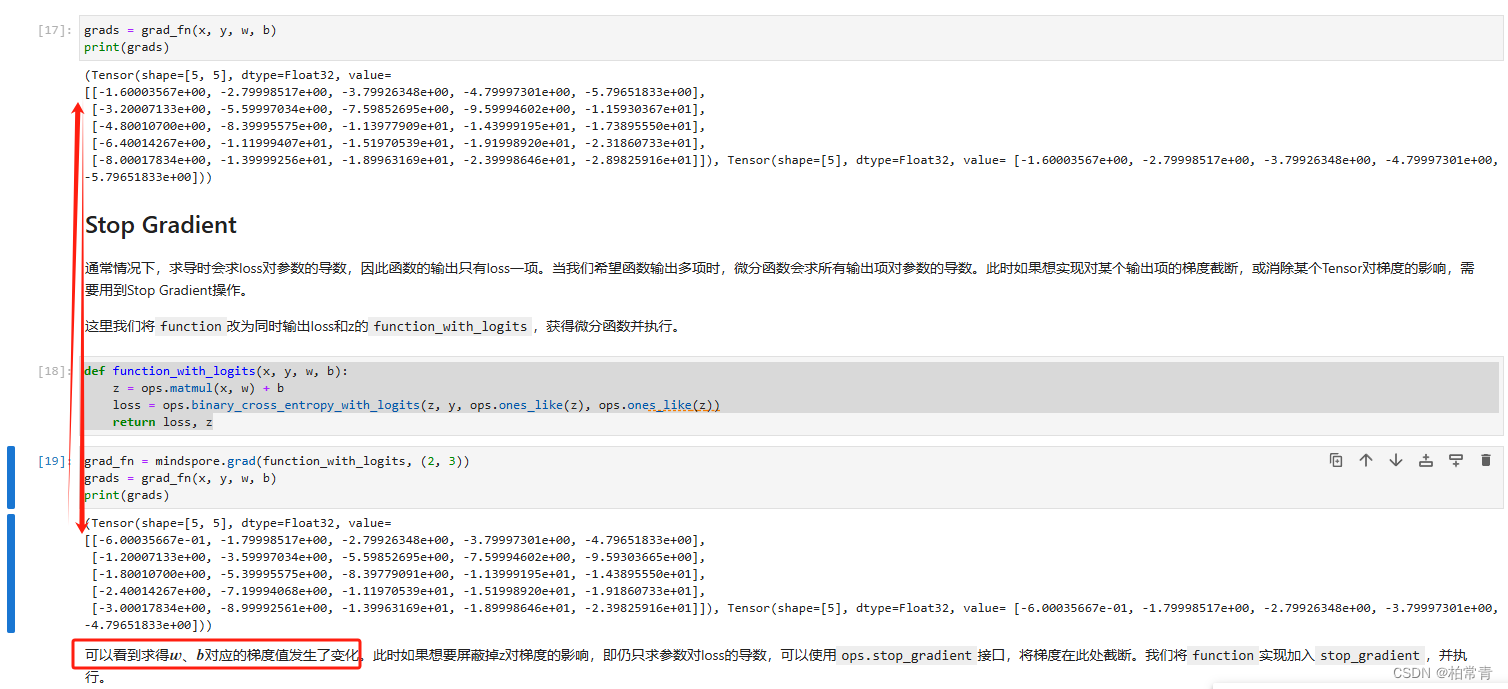
规避方式1：ops.stop_gradient(z)

def function_stop_gradient(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
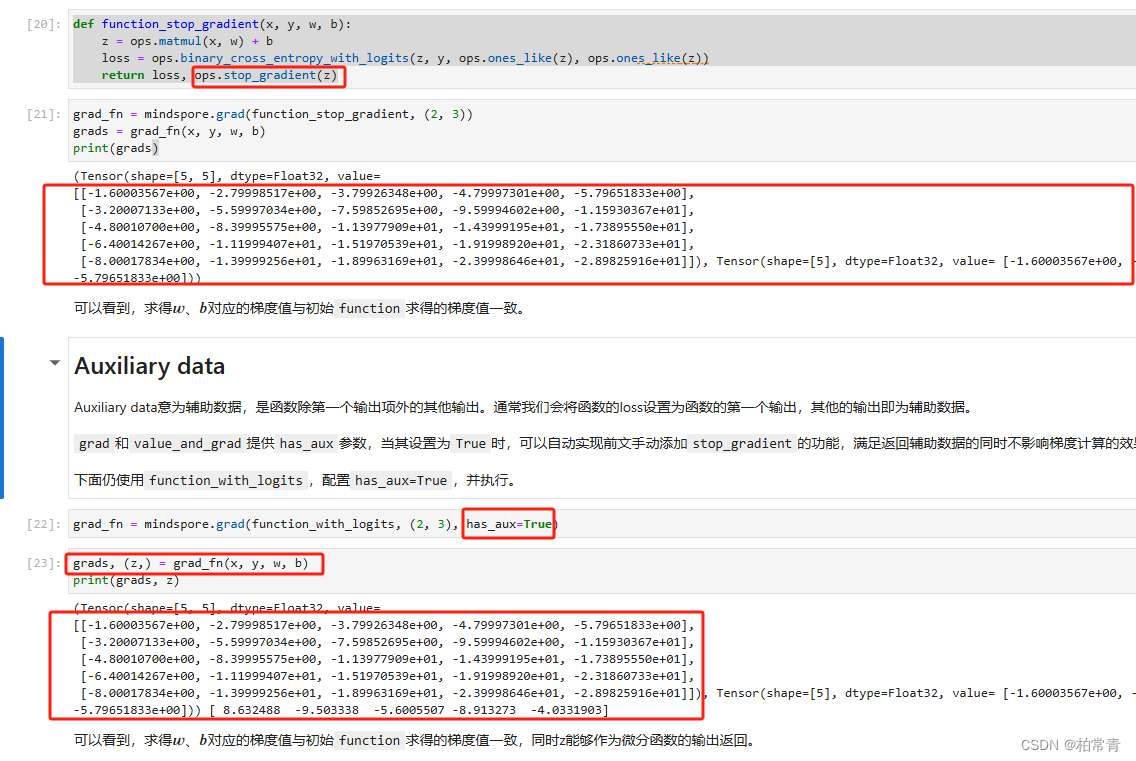
    return loss, ops.stop_gradient(z)

规避方式2

grad_fn = mindspore.grad(function_with_logits, (2, 3), has_aux=True)

执行结果：只计算了是函数的梯度。

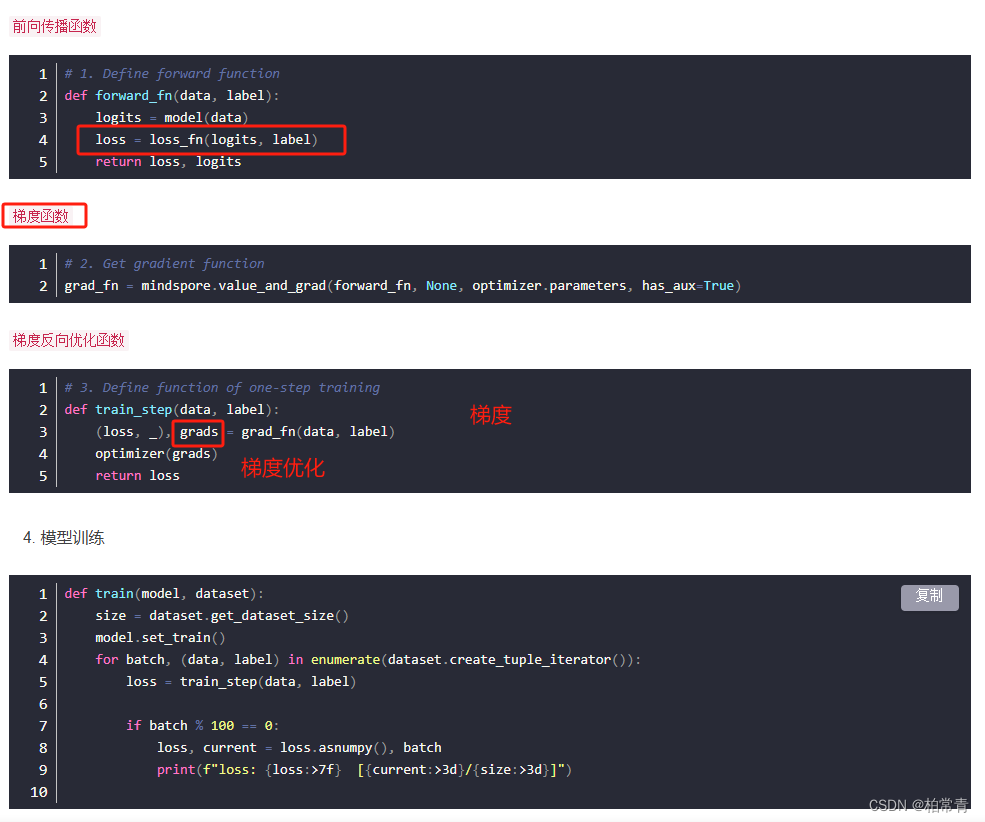
四、神经网络训练实践-手写数字识别

Mnist手写数字识别-第三节模型训练实践，有梯度计算，优化的详细使用细节。