摘要

本周阅读了一篇关于TCN和LSTM进行光伏功率预测的文章，本文提出了一种利用LSTM-TCN预测光伏功率的新模型。它由长短期记忆和时间卷积网络模型之间的组合组成。LSTM用于从输入数据中提取时态特征，然后与TCN结合，在特征和输出之间建立连接。与LSTM、TCN相比，平均绝对误差分别下降了、秋季8.47%，14.26%、冬季6.91%，15.18%、春季10.22%，实验结果表明，所提出的模型优于LSTM和TCN模型。与LSTM、TCN相比，平均绝对误差分别下降了、秋季8.47%，14.26%、冬季6.91%，15.18%、春季10.22%，14.26%和夏季14.26%，14.23%。 在多步预测方面，LSTM-TCN在2步到7步的光伏功率预测中均优于所有比较的模型。

ABSTRACT

This week, a paper on photovoltaic power prediction using Temporal Convolutional Network (TCN) and Long Short-Term Memory (LSTM) is readed. This paper puts forward a new model to predict photovoltaic power by using LSTM-TCN. It consists of a combination of long-term and short-term memory and time convolution network model. LSTM is used to extract temporal features from input data, and then combined with TCN to establish a connection between features and output. Compared with LSTM and TCN, the average absolute error decreased by 8.47% in autumn, 14.26% in winter, 6.91% in winter, 15.18% in spring and 10.22% in spring. The experimental results show that the proposed model is superior to LSTM and TCN models. Compared with LSTM and TCN, the average absolute error decreased by 8.47% in autumn, 14.26% in winter, 6.91% in winter, 15.18% in spring, 10.22% in spring, 14.26% in summer and 14.23% in summer. In the aspect of multi-step prediction, LSTM-TCN is superior to all the compared models in 2-step to 7-step photovoltaic power prediction.

文献阅读

题目

Accurate one step and multistep forecasting of very short-term PV power using LSTM-TCN model - ScienceDirect

问题

随着人口的增长和经济的发展，能源需求逐年增加。利用光伏发电能源作为清洁可再生能源可以满足这种能源需求的增加。光伏发电技术以其高性能、高效率、低成本的特点在世界范围内得到了广泛的应用。将光伏系统并入电网可以带来经济效益和环境效益。然而，由于太阳能的间歇性，这类能源的高渗透率也给电网系统带来了很多挑战。光伏发电预测是控制太阳能发电间歇性的最经济、最可行的解决方案之一。然而，由于光伏发电数据具有非线性和不稳定的特点，以及光伏发电所依赖的气象条件，准确预测是一项复杂的任务。光伏发电功率预测分为四个层次:长期预测为一个月至一年，中期预测为一周至一个月，短期预测为一周或一周以内，极短期或超短期预测为一分钟至几分钟。长期预测为光伏发电、输配电提供长期规划和决策，保证电力系统的可靠运行。中期预测为电力系统调度提供中期决策支持。短期预测为电力系统运行提供支持，提高了电力系统的可靠性。极短期预测用于电力平滑、实时电力调度和存储控制。

本文贡献

光伏发电预测主要有三种方法：物理方法、统计方法和混合方法。物理模型可以定义为具有描述系统输入和输出的数学方程的确定性模型。统计模型基于持久性的概念，通常依赖于机器学习和深度学习模型，这些模型可以从光伏发电历史数据中学习，并返回预测的光伏发电。对于混合模型，它是将前面的方法（物理模型和统计模型）相结合，以优化光伏功率预测的准确性。

本文提出的模型由长短时记忆和时态卷积网络模型结合而成。LSTM用于从输入数据中提取时间特征，然后结合TCN建立特征与输出之间的联系。所提出的模型已经使用包括测量的光伏功率的历史时间序列的数据集进行了测试。然后将该模式与LSTM和TCN模式在不同季节、时段预报、阴天、晴天和间歇日的预报精度进行了比较。

方法

本文提出了LSTM-TCN用于短期光伏功率预测，其中LSTM用于从输入数据中提取时间特征，而TCN用于将特征与输出联系起来用于光伏功率预测。这项工作所用的流程图如图2所示。

LSTM

ARIMA(自回归综合移动平均)是一种流行的时间序列预测模型，它基于这样一个事实，即未来预测是过去测量的线性函数。ARIMA模型的局限性在于它的线性度和它不依赖于旧值的事实，它只考虑了之前的状态。

传统的RNN模型存在梯度消失或梯度爆炸的问题。为了避免梯度消失问题，LSTM已被提出用于有效地处理时间序列数据。LSTM模型具有具有自连接的存储单元来存储时间状态。LSTM单元的结构如图3所示。Ct是内部单元状态。LSTM使用忘记门FT、输入门It和输出门Ot来维护、改变或删除单元状态信息。输入是每个时间戳t的序列向量xt、隐藏层输出ht−1和信元状态Ct−1。输出是LSTM隐藏层输出ht和信元状态Ct。忘记门、输入门和输出门使用公式(1)-(3)计算：

通过使用公式(4)计算当前候选状态Ct：

输入门和遗忘门确定Ct−1和̃Ct在当前信元状态Ct中分别占据的信息的比例。当前单元格状态可以通过公式(5)计算：

隐藏层输出通过公式(6)计算：

其中Wf、Wi和W0分别为遗忘门、输入门和输出门的权重矩阵。Bf、bi和b0分别是遗忘门、输入门和输出门偏置。
σ是激活函数。

TCN

TCN是一种用于具有因果约束的卷积神经网络，常用于时间序列预测任务。TCN的第一层是一维全卷积网络，其中每个中间层具有与输入层相同的大小，并且使用大小的零填充来获得与先前层相同的后续层的大小。与RNN类似，TCN体系结构可以处理任意长度的序列或时间序列，并将其映射到相同长度的输出数据。

TCN体系结构包括扩张的因果卷积，以尊重因果约束，提高各自的场，确保信息不会从未来泄漏到过去，并避免巨大的计算工作。
一维序列(x∈Rn)的元素S的扩张卷积运算F描述如下：

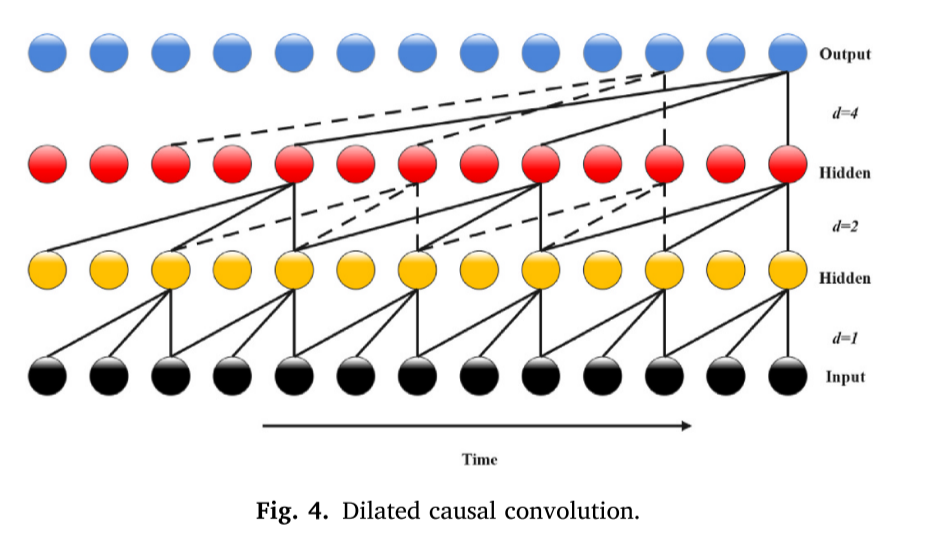
其中d是膨胀因子，i是滤波数，k是滤波片大小，∗是卷积运算符，S−d·i解释过去的方向。图4示出了具有扩张因子d=1、2、4和滤波器大小k=3的扩张因果卷积的例子。为了扩大网络的接收范围，增大了滤波器大小k和扩张因子d。接受范围越大，网络就越能充分考虑过去。

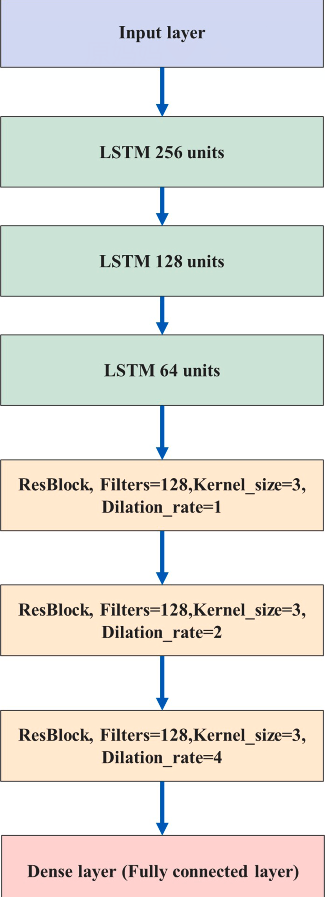
模型总体架构

论文提出的模型结合LSTM和TCN，利用其历史和气象数据(如全球水平辐射)来预测PV功率。LSTM-TCN的流程图如下图所示。该模型由三层LSTM模型组成，用于从输入数据中提取时间特征。第一层有256个单元，第二层有128个单元，第三层有64个单元。在LSTM层中加入3个堆叠的TCN模型残差块。每个残差块具有相同数量的Filter和内核大小。残差块的膨胀系数分别为1、2和4。将TCN模型与LSTM相结合，提高了预测精度，并建立了特征与输出之间的联系。最后，使用Dense层进行维度变换。用于模型训练和验证的损失函数是均方误差（MSE），模型优化器是自适应矩估计（Adam）。值得注意的是，LSTM和TCN参数是在使用Keras调谐器函数搜索误差最小的最优参数后，测试了膨胀率、内核大小、Filter数量、LSTM单元和层数等几个值后选择的。

实验

作者设置的参数如下：
100个epoch，batch size为200，学习率为0.001，损失函数是均方误差，用ADAM优化算法来降低损失函数，模型的输入顺序采用12步回溯，相当于1小时。

为了在时间序列预测中使用深度学习模型，必须将数据集转换为监督回归问题，其中输入特征和输出（标签）被呈现和定义。滑动窗口方法通过分割数据集来将数据集转换为监督学习问题，以获得一个序列（固定窗口大小）的观测值作为模型的输入，并获得固定数量的后续观测值作为输出，这些观测值可以是一步预测的一个后续观测值，也可以是多步预测的一系列后续观测值。通过每次滑动窗口一个时间步来对整个数据集重复分割，以获得下一个输入和输出序列。下图显示了多步时间序列预测（输入序列大小= 5，输出序列大小= 3）的滑动窗口过程。数据集分为训练数据集，用于训练所提出的深度学习模型和测试数据集，以评估模型的准确性和性能。

实验结果

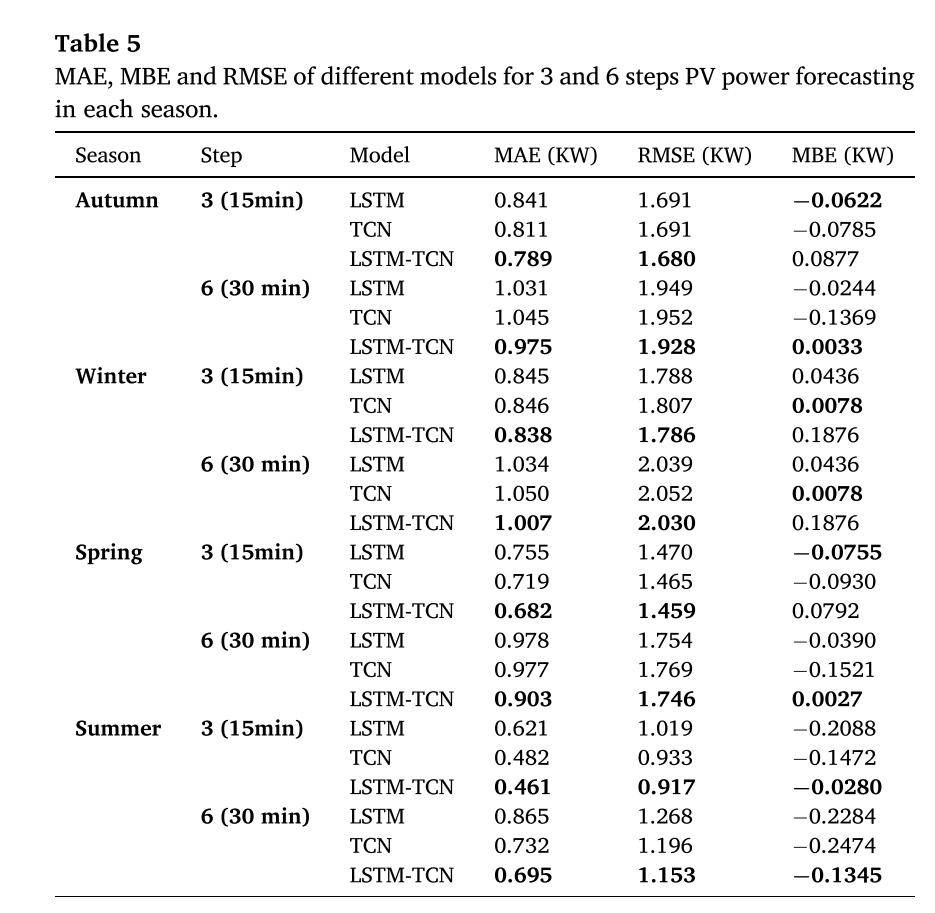
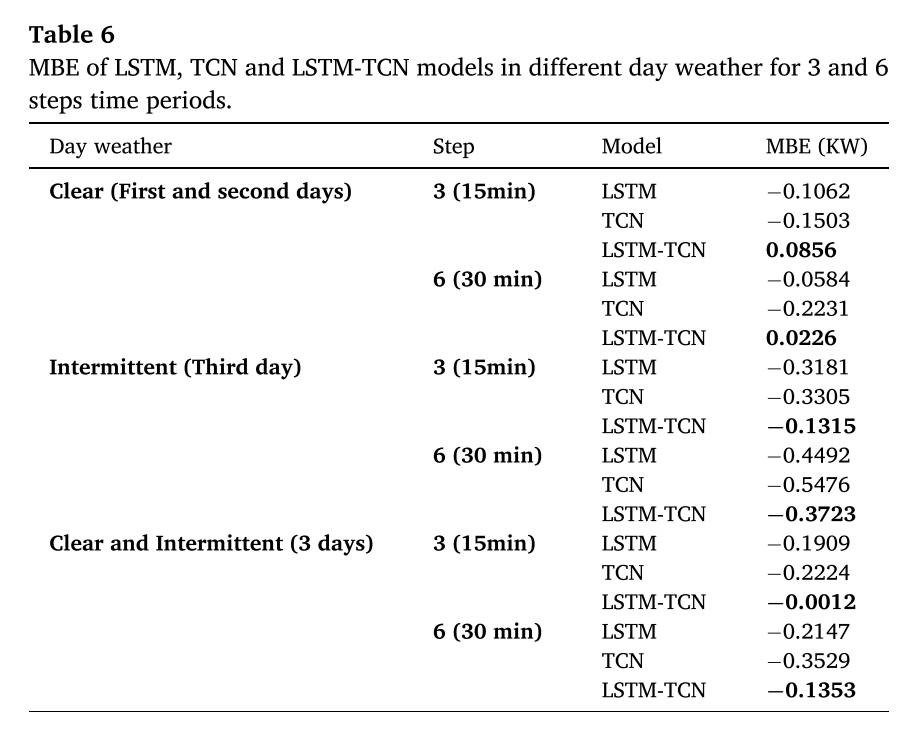
对于一步预测，结果表明作者提出的模型比LSTM和TCN模型具有更好的性能。与LSTM、TCN相比，秋季、冬季、春季和夏季的平均绝对误差分别降低了8.47%、14.26%、6.91%、15.18、10.22%、14.26%、14.23%。对于多步预测，从2步预测到7步预测，LSTM-TCN在不同时间段的预测均优于所有比较模型。

深度学习

TCN-LSTM代码

import argparse
import time
 
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from matplotlib import pyplot as plt
from torch.nn.utils import weight_norm
from torch.utils.data import DataLoader
from torch.utils.data import Dataset
from tqdm import tqdm
 
# 随机数种子
np.random.seed(0)
 
 
class StandardScaler():
    def __init__(self):
        self.mean = 0.
        self.std = 1.
 
    def fit(self, data):
        self.mean = data.mean(0)
        self.std = data.std(0)
 
    def transform(self, data):
        mean = torch.from_numpy(self.mean).type_as(data).to(data.device) if torch.is_tensor(data) else self.mean
        std = torch.from_numpy(self.std).type_as(data).to(data.device) if torch.is_tensor(data) else self.std
        return (data - mean) / std
 
    def inverse_transform(self, data):
        mean = torch.from_numpy(self.mean).type_as(data).to(data.device) if torch.is_tensor(data) else self.mean
        std = torch.from_numpy(self.std).type_as(data).to(data.device) if torch.is_tensor(data) else self.std
        if data.shape[-1] != mean.shape[-1]:
            mean = mean[-1:]
            std = std[-1:]
        return (data * std) + mean
 
 
def plot_loss_data(data):
    # 使用Matplotlib绘制线图
    plt.figure()
 
    plt.plot(data, marker='o')
 
    # 添加标题
    plt.title("loss results Plot")
 
    # 显示图例
    plt.legend(["Loss"])
 
    plt.show()
 
 
class TimeSeriesDataset(Dataset):
    def __init__(self, sequences):
        self.sequences = sequences
 
    def __len__(self):
        return len(self.sequences)
 
    def __getitem__(self, index):
        sequence, label = self.sequences[index]
        return torch.Tensor(sequence), torch.Tensor(label)
 
 
def create_inout_sequences(input_data, tw, pre_len, config):
    # 创建时间序列数据专用的数据分割器
    inout_seq = []
    L = len(input_data)
    for i in range(L - tw):
        train_seq = input_data[i:i + tw]
        if (i + tw + pre_len) > len(input_data):
            break
        if config.feature == 'MS':
            train_label = input_data[:, -1:][i + tw:i + tw + pre_len]
        else:
            train_label = input_data[i + tw:i + tw + pre_len]
        inout_seq.append((train_seq, train_label))
    return inout_seq
 
 
def calculate_mae(y_true, y_pred):
    # 平均绝对误差
    mae = np.mean(np.abs(y_true - y_pred))
    return mae
 
 
def create_dataloader(config, device):
    print(">>>>>>>>>>>>>>>>>>>>>>>>>>>>创建数据加载器<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<")
    df = pd.read_csv(config.data_path)  # 填你自己的数据地址,自动选取你最后一列数据为特征列 # 添加你想要预测的特征列
    pre_len = config.pre_len  # 预测未来数据的长度
    train_window = config.window_size  # 观测窗口
 
    # 将特征列移到末尾
    target_data = df[[config.target]]
    df = df.drop(config.target, axis=1)
    df = pd.concat((df, target_data), axis=1)
 
    cols_data = df.columns[1:]
    df_data = df[cols_data]
 
    # 这里加一些数据的预处理, 最后需要的格式是pd.series
    true_data = df_data.values
 
    # 定义标准化优化器
    # 定义标准化优化器
    scaler = StandardScaler()
    scaler.fit(true_data)
 
    train_data = true_data[int(0.3 * len(true_data)):]
    valid_data = true_data[int(0.15 * len(true_data)):int(0.30 * len(true_data))]
    test_data = true_data[:int(0.15 * len(true_data))]
    print("训练集尺寸:", len(train_data), "测试集尺寸:", len(test_data), "验证集尺寸:", len(valid_data))
 
    # 进行标准化处理
    train_data_normalized = scaler.transform(train_data)
    test_data_normalized = scaler.transform(test_data)
    valid_data_normalized = scaler.transform(valid_data)
 
    # 转化为深度学习模型需要的类型Tensor
    train_data_normalized = torch.FloatTensor(train_data_normalized).to(device)
    test_data_normalized = torch.FloatTensor(test_data_normalized).to(device)
    valid_data_normalized = torch.FloatTensor(valid_data_normalized).to(device)
 
    # 定义训练器的的输入
    train_inout_seq = create_inout_sequences(train_data_normalized, train_window, pre_len, config)
    test_inout_seq = create_inout_sequences(test_data_normalized, train_window, pre_len, config)
    valid_inout_seq = create_inout_sequences(valid_data_normalized, train_window, pre_len, config)
 
    # 创建数据集
    train_dataset = TimeSeriesDataset(train_inout_seq)
    test_dataset = TimeSeriesDataset(test_inout_seq)
    valid_dataset = TimeSeriesDataset(valid_inout_seq)
 
    # 创建 DataLoader
    train_loader = DataLoader(train_dataset, batch_size=args.batch_size, shuffle=True, drop_last=True)
    test_loader = DataLoader(test_dataset, batch_size=args.batch_size, shuffle=False, drop_last=True)
    valid_loader = DataLoader(valid_dataset, batch_size=args.batch_size, shuffle=False, drop_last=True)
 
    print("通过滑动窗口共有训练集数据：", len(train_inout_seq), "转化为批次数据:", len(train_loader))
    print("通过滑动窗口共有测试集数据：", len(test_inout_seq), "转化为批次数据:", len(test_loader))
    print("通过滑动窗口共有验证集数据：", len(valid_inout_seq), "转化为批次数据:", len(valid_loader))
    print(">>>>>>>>>>>>>>>>>>>>>>>>>>>>创建数据加载器完成<<<<<<<<<<<<<<<<<<<<<<<<<<<")
    return train_loader, test_loader, valid_loader, scaler
 
 
class Chomp1d(nn.Module):
    def __init__(self, chomp_size):
        super(Chomp1d, self).__init__()
        self.chomp_size = chomp_size
 
    def forward(self, x):
        return x[:, :, :-self.chomp_size].contiguous()
 
 
class TemporalBlock(nn.Module):
    def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
        super(TemporalBlock, self).__init__()
        self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp1 = Chomp1d(padding)
        self.relu1 = nn.ReLU()
        self.dropout1 = nn.Dropout(dropout)
 
        self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp2 = Chomp1d(padding)
        self.relu2 = nn.ReLU()
        self.dropout2 = nn.Dropout(dropout)
 
        self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
                                 self.conv2, self.chomp2, self.relu2, self.dropout2)
        self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
        self.relu = nn.ReLU()
        self.init_weights()
 
    def init_weights(self):
        self.conv1.weight.data.normal_(0, 0.01)
        self.conv2.weight.data.normal_(0, 0.01)
        if self.downsample is not None:
            self.downsample.weight.data.normal_(0, 0.01)
 
    def forward(self, x):
        out = self.net(x)
        res = x if self.downsample is None else self.downsample(x)
        return self.relu(out + res)
 
 
class TemporalConvNet(nn.Module):
    def __init__(self, num_inputs, outputs, pre_len, num_channels, n_layers, kernel_size=2, dropout=0.2):
        super(TemporalConvNet, self).__init__()
        layers = []
        self.pre_len = pre_len
        self.n_layers = n_layers
        self.hidden_size = num_channels[-2]
        self.hidden = nn.Linear(num_channels[-1], num_channels[-2])
        self.relu = nn.ReLU()
        self.lstm = nn.LSTM(self.hidden_size, self.hidden_size, n_layers, bias=True,
                            batch_first=True)  # output (batch_size, obs_len, hidden_size)
        num_levels = len(num_channels)
        for i in range(num_levels):
            dilation_size = 2 ** i
            in_channels = num_inputs if i == 0 else num_channels[i - 1]
            out_channels = num_channels[i]
            layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
                                     padding=(kernel_size - 1) * dilation_size, dropout=dropout)]
 
        self.network = nn.Sequential(*layers)
        self.linear = nn.Linear(num_channels[-2], outputs)
 
    def forward(self, x):
        x = x.permute(0, 2, 1)
        x = self.network(x)
        x = x.permute(0, 2, 1)
 
        batch_size, obs_len, features_size = x.shape  # (batch_size, obs_len, features_size)
        xconcat = self.hidden(x)  # (batch_size, obs_len, hidden_size)
        H = torch.zeros(batch_size, obs_len - 1, self.hidden_size).to(device)  # (batch_size, obs_len-1, hidden_size)
        ht = torch.zeros(self.n_layers, batch_size, self.hidden_size).to(
            device)  # (num_layers, batch_size, hidden_size)
        ct = ht.clone()
        for t in range(obs_len):
            xt = xconcat[:, t, :].view(batch_size, 1, -1)  # (batch_size, 1, hidden_size)
            out, (ht, ct) = self.lstm(xt, (ht, ct))  # ht size (num_layers, batch_size, hidden_size)
            htt = ht[-1, :, :]  # (batch_size, hidden_size)
            if t != obs_len - 1:
                H[:, t, :] = htt
        H = self.relu(H)  # (batch_size, obs_len-1, hidden_size)
 
        x = self.linear(H)
        return x[:, -self.pre_len:, :]
 
 
def train(model, args, scaler, device):
    start_time = time.time()  # 计算起始时间
    model = model
    loss_function = nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
    epochs = args.epochs
    model.train()  # 训练模式
    results_loss = []
    for i in tqdm(range(epochs)):
        losss = []
        for seq, labels in train_loader:
            optimizer.zero_grad()
 
            y_pred = model(seq)
 
            single_loss = loss_function(y_pred, labels)
 
            single_loss.backward()
 
            optimizer.step()
            losss.append(single_loss.detach().cpu().numpy())
        tqdm.write(f"\t Epoch {i + 1} / {epochs}, Loss: {sum(losss) / len(losss)}")
        results_loss.append(sum(losss) / len(losss))
 
 
        torch.save(model.state_dict(), 'save_model.pth')
        time.sleep(0.1)
 
    # valid_loss = valid(model, args, scaler, valid_loader)
    # 尚未引入学习率计划后期补上
    # 保存模型
 
    print(f">>>>>>>>>>>>>>>>>>>>>>模型已保存,用时:{(time.time() - start_time) / 60:.4f} min<<<<<<<<<<<<<<<<<<")
    plot_loss_data(results_loss)
 
 
def valid(model, args, scaler, valid_loader):
    lstm_model = model
    # 加载模型进行预测
    lstm_model.load_state_dict(torch.load('save_model.pth'))
    lstm_model.eval()  # 评估模式
    losss = []
 
    for seq, labels in valid_loader:
        pred = lstm_model(seq)
        mae = calculate_mae(pred.detach().numpy().cpu(), np.array(labels.detach().cpu()))  # MAE误差计算绝对值(预测值  - 真实值)
        losss.append(mae)
 
    print("验证集误差MAE:", losss)
    return sum(losss) / len(losss)
 
 
def test(model, args, test_loader, scaler):
    # 加载模型进行预测
    losss = []
    model = model
    model.load_state_dict(torch.load('save_model.pth'))
    model.eval()  # 评估模式
    results = []
    labels = []
    for seq, label in test_loader:
        pred = model(seq)
        mae = calculate_mae(pred.detach().cpu().numpy(),
                            np.array(label.detach().cpu()))  # MAE误差计算绝对值(预测值  - 真实值)
        losss.append(mae)
        pred = pred[:, 0, :]
        label = label[:, 0, :]
        pred = scaler.inverse_transform(pred.detach().cpu().numpy())
        label = scaler.inverse_transform(label.detach().cpu().numpy())
        for i in range(len(pred)):
            results.append(pred[i][-1])
            labels.append(label[i][-1])
 
    print("测试集误差MAE:", losss)
    # 绘制历史数据
    plt.plot(labels, label='TrueValue')
 
    # 绘制预测数据
    # 注意这里预测数据的起始x坐标是历史数据的最后一个点的x坐标
    plt.plot(results, label='Prediction')
 
    # 添加标题和图例
    plt.title("test state")
    plt.legend()
    plt.show()
 
 
# 检验模型拟合情况
def inspect_model_fit(model, args, train_loader, scaler):
    model = model
    model.load_state_dict(torch.load('save_model.pth'))
    model.eval()  # 评估模式
    results = []
    labels = []
 
    for seq, label in train_loader:
        pred = model(seq)[:, 0, :]
        label = label[:, 0, :]
        pred = scaler.inverse_transform(pred.detach().cpu().numpy())
        label = scaler.inverse_transform(label.detach().cpu().numpy())
        for i in range(len(pred)):
            results.append(pred[i][-1])
            labels.append(label[i][-1])
 
    # 绘制历史数据
    plt.plot(labels, label='History')
 
    # 绘制预测数据
    # 注意这里预测数据的起始x坐标是历史数据的最后一个点的x坐标
    plt.plot(results, label='Prediction')
 
    # 添加标题和图例
    plt.title("inspect model fit state")
    plt.legend()
    plt.show()
 
 
def predict(model, args, device, scaler):
    # 预测未知数据的功能
    df = pd.read_csv(args.data_path)
    df = df.iloc[:, 1:][-args.window_size:].values  # 转换为nadarry
    pre_data = scaler.transform(df)
    tensor_pred = torch.FloatTensor(pre_data).to(device)
    tensor_pred = tensor_pred.unsqueeze(0)  # 单次预测 , 滚动预测功能暂未开发后期补上
    model = model
    model.load_state_dict(torch.load('save_model.pth'))
    model.eval()  # 评估模式
 
    pred = model(tensor_pred)[0]
 
    pred = scaler.inverse_transform(pred.detach().cpu().numpy())
 
    # 假设 df 和 pred 是你的历史和预测数据
 
    # 计算历史数据的长度
    history_length = len(df[:, -1])
 
    # 为历史数据生成x轴坐标
    history_x = range(history_length)
 
    # 为预测数据生成x轴坐标
    # 开始于历史数据的最后一个点的x坐标
    prediction_x = range(history_length - 1, history_length + len(pred[:, -1]) - 1)
 
    # 绘制历史数据
    plt.plot(history_x, df[:, -1], label='History')
 
    # 绘制预测数据
    # 注意这里预测数据的起始x坐标是历史数据的最后一个点的x坐标
    plt.plot(prediction_x, pred[:, -1], marker='o', label='Prediction')
    plt.axvline(history_length - 1, color='red')  # 在图像的x位置处画一条红色竖线
    # 添加标题和图例
    plt.title("History and Prediction")
    plt.legend()
 
 
if __name__ == '__main__':
    parser = argparse.ArgumentParser(description='Time Series forecast')
    parser.add_argument('-model', type=str, default='TCN-LSTM', help="模型持续更新")
    parser.add_argument('-window_size', type=int, default=126, help="时间窗口大小, window_size > pre_len")
    parser.add_argument('-pre_len', type=int, default=24, help="预测未来数据长度")
    # data
    parser.add_argument('-shuffle', action='store_true', default=True, help="是否打乱数据加载器中的数据顺序")
    parser.add_argument('-data_path', type=str, default='ETTh1-Test.csv', help="你的数据数据地址")
    parser.add_argument('-target', type=str, default='OT', help='你需要预测的特征列，这个值会最后保存在csv文件里')
    parser.add_argument('-input_size', type=int, default=7, help='你的特征个数不算时间那一列')
    parser.add_argument('-feature', type=str, default='MS', help='[M, S, MS],多元预测多元,单元预测单元,多元预测单元')
    parser.add_argument('-model_dim', type=list, default=[64, 128, 256], help='这个地方是这个TCN卷积的关键部分,它代表了TCN的层数我这里输'
                                                                              '入list中包含三个元素那么我的TCN就是三层，这个根据你的数据复杂度来设置'
                                                                              '层数越多对应数据越复杂但是不要超过5层')
 
    # learning
    parser.add_argument('-lr', type=float, default=0.001, help="学习率")
    parser.add_argument('-drop_out', type=float, default=0.05, help="随机丢弃概率,防止过拟合")
    parser.add_argument('-epochs', type=int, default=20, help="训练轮次")
    parser.add_argument('-batch_size', type=int, default=16, help="批次大小")
    parser.add_argument('-save_path', type=str, default='models')
 
    # model
    parser.add_argument('-hidden_size', type=int, default=64, help="隐藏层单元数")
    parser.add_argument('-kernel_sizes', type=int, default=3)
    parser.add_argument('-laryer_num', type=int, default=1)
    # device
    parser.add_argument('-use_gpu', type=bool, default=True)
    parser.add_argument('-device', type=int, default=0, help="只设置最多支持单个gpu训练")
 
    # option
    parser.add_argument('-train', type=bool, default=True)
    parser.add_argument('-test', type=bool, default=True)
    parser.add_argument('-predict', type=bool, default=True)
    parser.add_argument('-inspect_fit', type=bool, default=True)
    parser.add_argument('-lr-scheduler', type=bool, default=True)
    args = parser.parse_args()
 
    if isinstance(args.device, int) and args.use_gpu:
        device = torch.device("cuda:" + f'{args.device}')
    else:
        device = torch.device("cpu")
    print("使用设备:", device)
    train_loader, test_loader, valid_loader, scaler = create_dataloader(args, device)
 
    if args.feature == 'MS' or args.feature == 'S':
        args.output_size = 1
    else:
        args.output_size = args.input_size
 
    # 实例化模型
    try:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始初始化{args.model}模型<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        model = TemporalConvNet(args.input_size, args.output_size, args.pre_len, args.model_dim, args.laryer_num,
                                args.kernel_sizes).to(device)
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始初始化{args.model}模型成功<<<<<<<<<<<<<<<<<<<<<<<<<<<")
    except:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始初始化{args.model}模型失败<<<<<<<<<<<<<<<<<<<<<<<<<<<")
 
    # 训练模型
    if args.train:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始{args.model}模型训练<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        train(model, args, scaler, device)
    if args.test:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始{args.model}模型测试<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        test(model, args, test_loader, scaler)
    if args.inspect_fit:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>开始检验{args.model}模型拟合情况<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        inspect_model_fit(model, args, train_loader, scaler)
    if args.predict:
        print(f">>>>>>>>>>>>>>>>>>>>>>>>>预测未来{args.pre_len}条数据<<<<<<<<<<<<<<<<<<<<<<<<<<<")
        predict(model, args, device, scaler)
    plt.show()

运行结果

总结

时序卷积与普通的一维卷积存在以下两点不同：

1. 使用因果卷积。特点在于网络输出长度等于输入长度，保证未来信息不会用于预测。
2. 采用扩张卷积。特点在于可通过增加层数和扩张卷积核大小来增大感受野。越到上层，卷积核越大，输出的信息范围越广，从而确保滤波器能够获得更大范围输入特征，高效获取长时间跨度信息。