清楚姐姐学信息论
数学,只需要求x的y次方和y的x次方那个大选哪个,除了2和3时是3多,其他情况都是数越小能代表的数越多
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int x, y;
cin >> x >> y;
int maxx = max(x, y), minn = min(x, y);
if (maxx == 3 && minn == 2) {
cout << 3 << '\n';
} else {
cout << minn << '\n';
}
return 0;
}清楚姐姐学构造
通过同余方程式可以看出,a是关于中点对称的,b的绝对值是关于中点对称的
因为
c[i]=a[i]+b[i]
所以
c[i]+c[n-1-i]=2*a[i]
c[n-1-i]-c[i]=2*b[i]
有了上述计算公式,发现c[i]+c[n-1-i]和c[n-1-i]-c[i]必须都是偶数才行,因为模数m一定是质数,也可知的是质数除了2都是奇素数,因此,除了2一定存在若干个m可以把c[i]+c[n-1-i]和c[n-1-i]-c[i]变成偶数来得到a[i],b[i],但如果是2,则不可能,所以当m=2时如果存在奇数,则输出No
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<int> x, y;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
if (n == 1) {
cout << "Yes\n";
cout << a[0] << '\n';
cout << "0\n";
return 0;
}
if (m == 2) {
for (int i = 0; i < n / 2; i++) {
if ((a[i] + a[n - 1 - i]) % 2 == 1) {
cout << "No\n";
return 0;
}
int p = (a[i] + a[n - 1 - i]) / 2;
x.push_back(p % m);
if (((a[n - 1 - i] - a[i] + m) % m) % 2 == 1) {
cout << "No\n";
return 0;
}
p = ((a[n - 1 - i] - a[i] + m) % m) / 2;
y.push_back(p % m);
}
if (n & 1) {
x.push_back(a[n / 2]);
y.push_back(0);
cout << "Yes\n";
for (int i = 0; i <= n / 2; i++) {
cout << x[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << x[i] << " \n"[i == 0];
}
for (int i = 0; i <= n / 2; i++) {
cout << m - y[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << y[i] << " \n"[i == 0];
}
} else {
cout << "Yes\n";
for (int i = 0; i < n / 2; i++) {
cout << x[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << x[i] << " \n"[i == 0];
}
for (int i = 0; i < n / 2; i++) {
cout << m - y[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << y[i] << " \n"[i == 0];
}
}
return 0;
}
if (n & 1) {
for (int i = 0; i < n / 2; i++) {
int p = (a[i] + a[n - 1 - i]);
while (p & 1) {
p += m;
}
x.push_back(p / 2 % m);
p = (a[n - 1 - i] - a[i] + m) % m;
while (p & 1) {
p += m;
}
y.push_back(p / 2 % m);
}
x.push_back(a[n / 2]);
y.push_back(0);
cout << "Yes\n";
for (int i = 0; i <= n / 2; i++) {
cout << x[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << x[i] << " \n"[i == 0];
}
for (int i = 0; i <= n / 2; i++) {
cout << m - y[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << y[i] << " \n"[i == 0];
}
} else {
for (int i = 0; i < n / 2; i++) {
int p = (a[i] + a[n - 1 - i]);
while (p & 1) {
p += m;
}
x.push_back(p / 2 % m);
p = (a[n - 1 - i] - a[i] + m) % m;
while (p & 1) {
p += m;
}
y.push_back(p / 2 % m);
}
x.push_back(a[n / 2]);
y.push_back(0);
cout << "Yes\n";
for (int i = 0; i < n / 2; i++) {
cout << x[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << x[i] << " \n"[i == 0];
}
for (int i = 0; i < n / 2; i++) {
cout << m - y[i] << " ";
}
for (int i = n / 2 - 1; i >= 0; i--) {
cout << y[i] << " \n"[i == 0];
}
}
return 0;
}清楚姐姐学01背包(Easy Version)
01背包,因为数据范围比较小,可以n的3次方暴力通过,即在01背包的基础上多了一维枚举去掉的是哪一个蝴蝶结,即dp[i][j]表示的是去掉第i个蝴蝶结后的n-1个蝴蝶结中,体积为j的最大好看程度总和
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<pair<int, int>> a(n + 1);
int sum = 0;
for (int i = 1; i <= n; i++) {
cin >> a[i].first >> a[i].second;
sum = max(sum, a[i].second);
}
vector<int> dp1(m + 2);
for (int i = 1; i <= n; i++) {
for (int j = m; j >= a[i].first; j--) {
dp1[j] = max(dp1[j], dp1[j - a[i].first] + a[i].second);
}
}
vector<vector<int>> dp(n + 1, vector<int> (m + 2));
int maxx = *max_element(dp1.begin(), dp1.end());
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
if (i == k) {
continue;
}
for (int j = m; j >= a[i].first; j--) {
dp[k][j] = max(dp[k][j], dp[k][j - a[i].first] + a[i].second);
}
}
}
for (int i = 1; i <= n; i++) {
int max1 = *max_element(dp[i].begin(), dp[i].end());
if (max1 != maxx) {
cout << "0\n";
} else {
int ans = 1e18;
for (int j = 0; j <= m - a[i].first; j++) {
ans = min(ans, maxx - dp[i][j] + 1 - a[i].second);
}
cout << ans << '\n';
}
}
return 0;
}清楚姐姐学01背包(Hard Version)
考虑降低时间复杂度为n方,dp[i][j]就是前i个蝴蝶结选择重量为j的所能得到的最大好看程度总和或后i个蝴蝶结选择重量为j的所能得到的最大好看程度总和,这样就能够得到dp[i-1][j]+dp[i+1][m-j],即去掉第i个蝴蝶结以后能到达的最大好看程度总和,dp[i-1][j]+dp[i+1][m-j-w[i]]也就是为第i个蝴蝶结留出空间但并未计算最大好看程度时的好看程度
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<int> w(n + 1), v(n + 1);
for (int i = 1; i <= n; i++) {
cin >> w[i] >> v[i];
}
int maxx = 0;
vector<vector<int>> dp1(n + 2,vector<int> (m + 1)), dp2(n + 2, vector<int> (m + 1));
for (int i = 1; i <= n; i++) {
dp1[i] = dp1[i - 1];
for (int j = m; j >= w[i]; j--) {
dp1[i][j] = max(dp1[i][j], dp1[i - 1][j - w[i]] + v[i]);
maxx = max(dp1[i][j], maxx);
}
}
for (int i = n; i >= 1; i--) {
dp2[i] = dp2[i + 1];
for (int j = m; j >= w[i]; j--) {
dp2[i][j] = max(dp2[i][j], dp2[i + 1][j - w[i]] + v[i]);
}
}
for (int i = 1; i <= n; i++) {
int max1 = 0, max2 = 0;
for (int j = 0; j <= m; j++) {
max1 = max(max1, dp1[i - 1][j] + dp2[i + 1][m - j]);
}
for (int j = 0; j <= m - w[i]; j++) {
max2 = max(max2, dp1[i - 1][j] + dp2[i + 1][m - j - w[i]]);
}
if (max1 != maxx) {
cout << "0\n";
} else {
cout << maxx - max2 - v[i] + 1 << '\n';
}
}
return 0;
}清楚姐姐打怪升级
根据题意可以发现,当a>=h[i]的时候,可以一秒秒杀怪,当h[i]>a的时候,能杀死怪的前提是a-v[i]*t>0,否则每次攻击后怪都能把血量恢复起来
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
LL n, t, a;
cin >> n >> t >> a;
vector<pair<LL, LL>> x(n);
LL ans = 0;
for (int i = 0; i < n; i++) {
cin >> x[i].first >> x[i].second;
}
for (int i = 0; i < n; i++) {
if (i == 0) {
if (x[i].first <= a) {
ans = 1;
} else {
ans = 1;
x[i].first -= a;
if (x[i].second * t >= a) {
ans = -1;
break;
} else {
LL p = a - x[i].second * t, z = (x[i].first + p - 1) / p;
ans += z * t;
}
}
} else {
if (x[i].first <= a) {
ans += t;
} else {
x[i].first -= a;
ans += t;
if (x[i].second * t >= a) {
ans = -1;
break;
} else {
LL p = a - x[i].second * t, z = (x[i].first + p - 1) / p;
ans += z * t;
}
}
}
}
cout << ans << '\n';
return 0;
}清楚姐姐学树状数组
根据题意,二叉树中序遍历的结果是1~n,所以只需要考虑前序和后序遍历的结果。
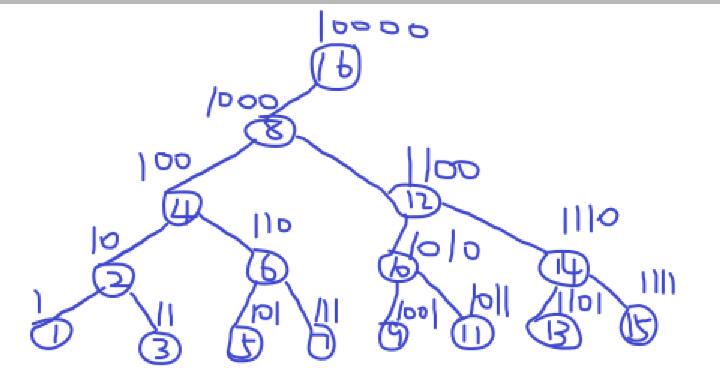
根据这张图我们可以看出,我们能够计算出一个数到根的路径,即对于一个从低位往高位走的二进制,如果当前位为1的,如果他的高一位的二进制位仍然是1,那么去往根的下一个结点就是把这一位变成0,如果他的高一位的二进制位为0,去往根的下一个结点就是在加一个lowbit,从而我们得到了从某一结点到根的路径,这样我们就可以从根再往要求的结点走,可知,如果当前结点的值大于x,说明x在左子树,否则在右子树上,对于前序遍历,往左子树走,步数只需要+1,而往右子树走的话需要把左子树的儿子节点个数及其父节点都加上,也就是lowbit(当前节点编号)。再考虑后序遍历,如果当前节点编号小于x,说明x在右子树,因为是后序遍历,所以需要加上左子树的儿子节点个数,如果走到了x,并且x为奇数,可知x为叶子节点,不存在子树,不需要操作,如果x为偶数,说明x不是叶子节点,存在子树,所以需要加上x的儿子节点个数,即(lowbit(x)-1)*2
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
#define lowbit(x) (x & (-x))
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
map<int, int> mp;
int res = 1;
mp[1] = 0;
for (int i = 1; i <= 61; i++) {
res <<= 1;
mp[res] = i;
}
int k, q;
cin >> k >> q;
while (q--) {
int x, y;
cin >> x;
if (x == (1LL << k)) {
cout << 1 << " " << (1LL << k) << " " << (1LL << k) << '\n';
continue;
}
y = x;
int ans = 1, ans1 = 1;
vector<int> z;
z.push_back(x);
for (int i = mp[lowbit(x)] + 1; i <= 61; i++) {
if (x >= (1LL << k)) {
break;
}
if (x >> i & 1 && x >> (i - 1) & 1) {
x -= lowbit(x);
z.push_back(x);
} else if ((x >> i) % 2 == 0 && (x >> (i - 1)) & 1) {
x += lowbit(x);
z.push_back(x);
} else {
break;
}
}
int len = z.size();
for (int i = len - 1; i > 0; i--) {
if (y > z[i]) {
ans += lowbit(z[i]);
} else {
ans++;
}
}
for (int i = len - 1; i >= 0; i--) {
if (y > z[i]) {
ans1 += lowbit(z[i]) - 1;
} else if (y == z[i] && y % 2 == 0) {
ans1 += (lowbit(z[i]) - 1) * 2;
}
}
cout << ans << " " << y << " " << ans1 << "\n";
}
return 0;
}清楚姐姐逛街(Easy Version)
先把智乃所能到达每个点的最短时间bfs计算出来,然后每次询问暴力查找步数最少的点并且清楚姐姐用的步数不少于智乃哥哥
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
struct node {
int x, y;
};
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m, q;
node st;
cin >> n >> m >> st.x >> st.y >> q;
st.x++;
st.y++;
vector<vector<char>> mp(n + 1, vector<char> (m + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> mp[i][j];
}
}
vector<vector<int>> dist(n + 1, vector<int> (m + 1, -1));
queue<node> qu;
qu.push(st);
dist[st.x][st.y] = 0;
while (!qu.empty()) {
node now = qu.front();
qu.pop();
for (int i = 0; i < 4; i++) {
node nxt;
nxt.x = now.x + dx[i];
nxt.y = now.y + dy[i];
if (mp[nxt.x][nxt.y] == '#' || dist[nxt.x][nxt.y] != -1) {
continue;
}
dist[nxt.x][nxt.y] = dist[now.x][now.y] + 1;
qu.push(nxt);
}
}
while (q--) {
node p;
cin >> p.x >> p.y;
p.x++;
p.y++;
int ans = -1;
for (int i = 0; i <= n * m; i++) {
if (dist[p.x][p.y] != -1 && i >= dist[p.x][p.y]) {
ans = i;
break;
}
if (mp[p.x][p.y] == '.') {
continue;
}
node nxt = p;
if (mp[nxt.x][nxt.y] == 'U') {
nxt.x--;
} else if (mp[nxt.x][nxt.y] == 'D') {
nxt.x++;
} else if (mp[nxt.x][nxt.y] == 'L') {
nxt.y--;
} else if (mp[nxt.x][nxt.y] == 'R') {
nxt.y++;
}
if (mp[nxt.x][nxt.y] != '#') {
p = nxt;
}
}
cout << ans << '\n';
}
return 0;
}清楚姐姐学排序
根据这个关系式,可以建立双层有向图,一层方向代表着大于关系,一层方向代表着小于关系,枚举根,dfs记录有多少数比根大,多少数比根小,如果两者之和为n-1个数,说明其他任意数都能通过种种关系,与根形成一种大于或小于关系,那么根的大小关系就是确定的
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<vector<int>> G(n + 1), G1(n + 1);
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
G[u].push_back(v);
G1[v].push_back(u);
}
vector<int> a(n + 1), b(n + 1);
for (int i = 1; i <= n; i++) {
vector<bool> vis(n + 1);
int sum = 0;
function<void(int)> dfs1 = [&](int u) {
vis[u] = true;
sum++;
for (auto v : G[u]) {
if (!vis[v]) {
dfs1(v);
}
}
};
dfs1(i);
a[i] = sum;
sum = 0;
vector<bool> vis1(n + 1);
function<void(int)> dfs2 = [&](int u) {
vis1[u] = true;
sum++;
for (auto v : G1[u]) {
if (!vis1[v]) {
dfs2(v);
}
}
};
dfs2(i);
b[i] = sum;
}
vector<int> ans(n + 1, -1);
for (int i = 1; i <= n; i++) {
if (n + 1 == a[i] + b[i]) {
ans[b[i]] = i;
}
}
for (int i = 1; i <= n; i++) {
cout << ans[i] << " \n"[i == n];
}
return 0;
}清楚姐姐的三角形I
因为
Va=Lb+Lc
Vb=La+Lc
Vc=La+Lb
所以联立可得
2*La=Vb+Vc-Va
2*Lb=Va+Vc-Vb
2*Lc=Va+Vb-Vc
因此,如果有奇数则不可能成立,并且如果边有小于等于0的也不成立,两条较小的边的和必须大于最大的边,注意输出顺序
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define int long long
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
LL x, y, z;
cin >> x >> y >> z;
vector<LL> a(3);
LL sum = x + y + z;
if (sum % 2 == 1) {
cout << "No\n";
continue;
}
sum /= 2;
LL xx = sum - x, yy = sum - y, zz = sum - z;
a[0] = sum - x;
a[1] = sum - y;
a[2] = sum - z;
sort(a.begin(), a.end());
if (a[0] <= 0) {
cout << "No\n";
} else if (a[0] + a[1] <= a[2]) {
cout << "No\n";
} else {
cout << "Yes\n";
cout << xx << " " << yy << " " << zz << '\n';
}
}
return 0;
}清楚姐姐的三角形II
很多种构造方式,只要不满足三角形即可
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<int> a(45);
a[1] = 1, a[2] = 1;
for (int i = 3; i <= 44; i++) {
a[i] = a[i - 1] + a[i - 2];
}
int x = n / 44, y = n % 44;
for (int i = 0; i < x; i++) {
for (int j = 1; j <= 44; j++) {
cout << a[j] << " ";
}
}
for (int i = 1; i <= y; i++) {
cout << a[i] << " ";
}
cout << '\n';
return 0;
}







![[思考进阶]05 人与人之间的差距,在于“自律”](https://img-blog.csdnimg.cn/8dba89f8f0a446a1a0df9e53a0666593.png#pic_center)