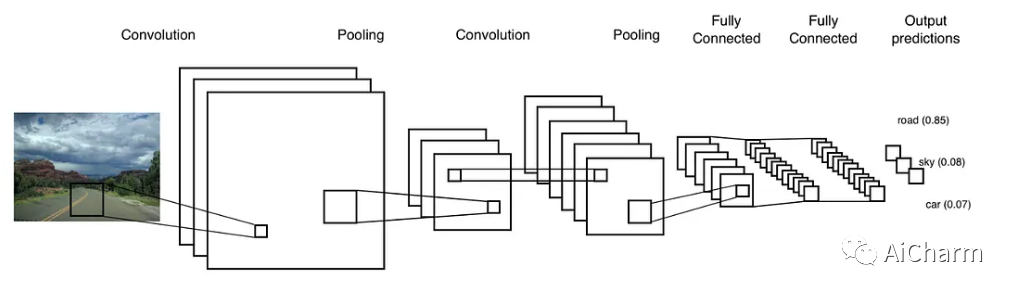
​卷积神经网络是一种深度学习概念，专为处理图像而构建。机器学习是计算机从过去的经验中学习的概念。深度学习是机器学习的高级部分。CNN 旨在寻找视觉模式。

• 当我们人类看到图像时，我们看到物体、颜色等。我们在成长过程中学习这些东西，但计算机只能理解 0 和 1，即二进制值。那么计算机将如何看到图像呢？

• 每个图像都是由像素组成的。下图很好地描述了计算机如何读取图像。有两种类型的图像，灰度和彩色。灰度（黑色和白色）由范围从 0 到 255（黑色到白色）的值数组组成。彩色图像有 3 个数组，红色数组、绿色数组和蓝色数组 (RGB)。这些数组中的每一个都在 0 到 255 之间（黑色到相应的颜色）。

MIT深度学习第3讲

架构

卷积神经网络有3种类型的层：卷积层、池化层和全连接层。

卷积层

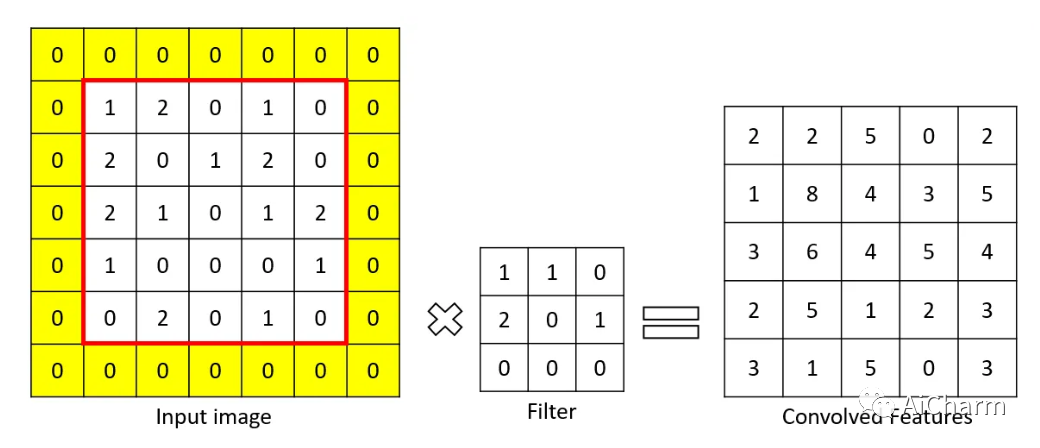
卷积层是从输入图像中提取重要特征的层。该层使用一个小方块来从输入图像中提取特征。这个小方块被称为内核或过滤器。解释一下，这一层在输入图像和过滤器之间有一个数学运算，以便保留和提取特征。这被称为CNN中的特征提取。

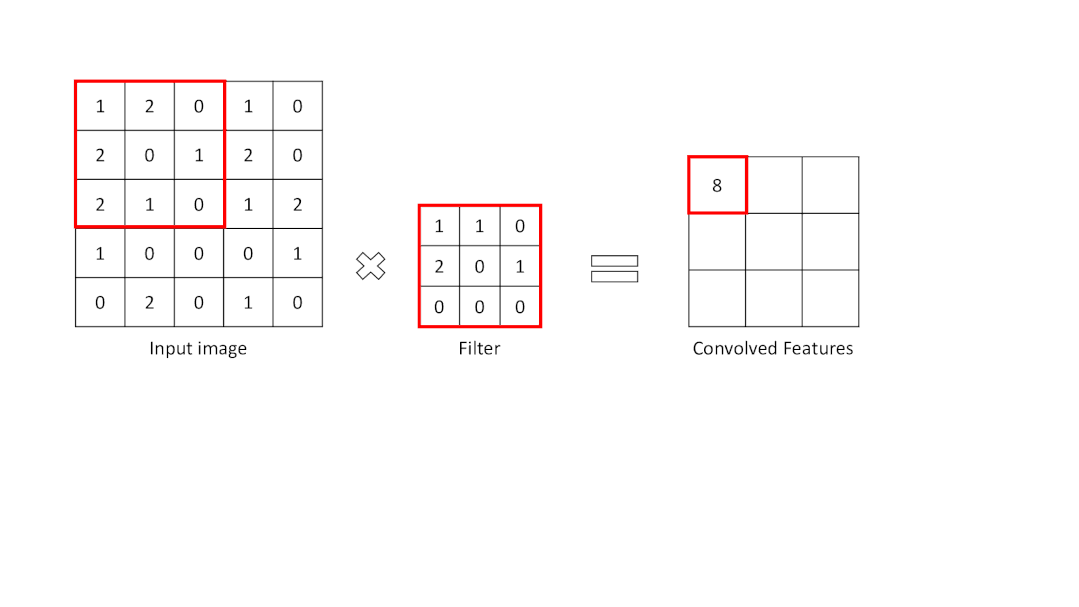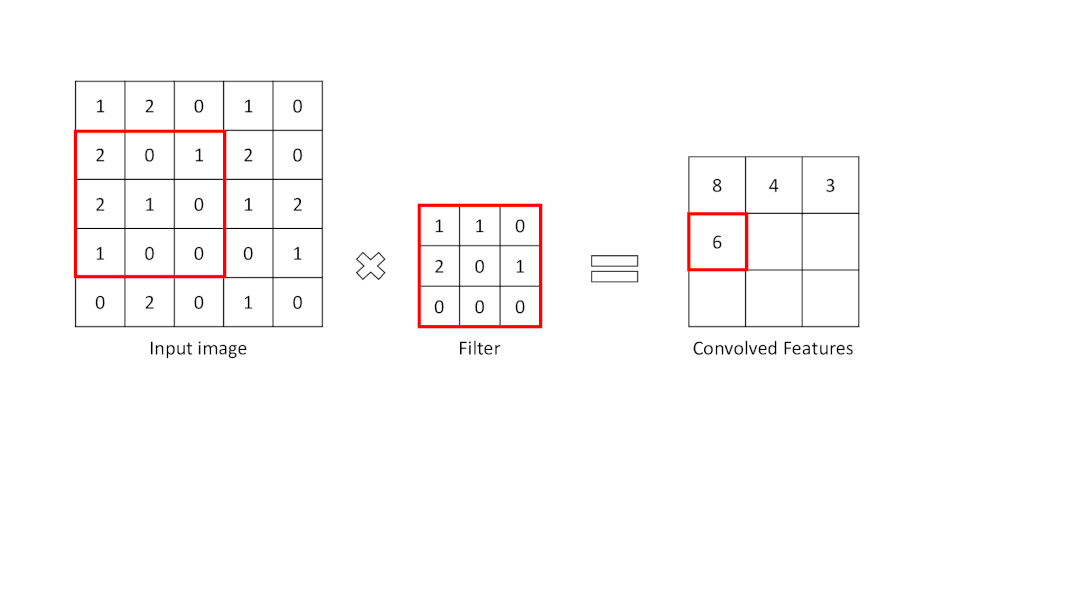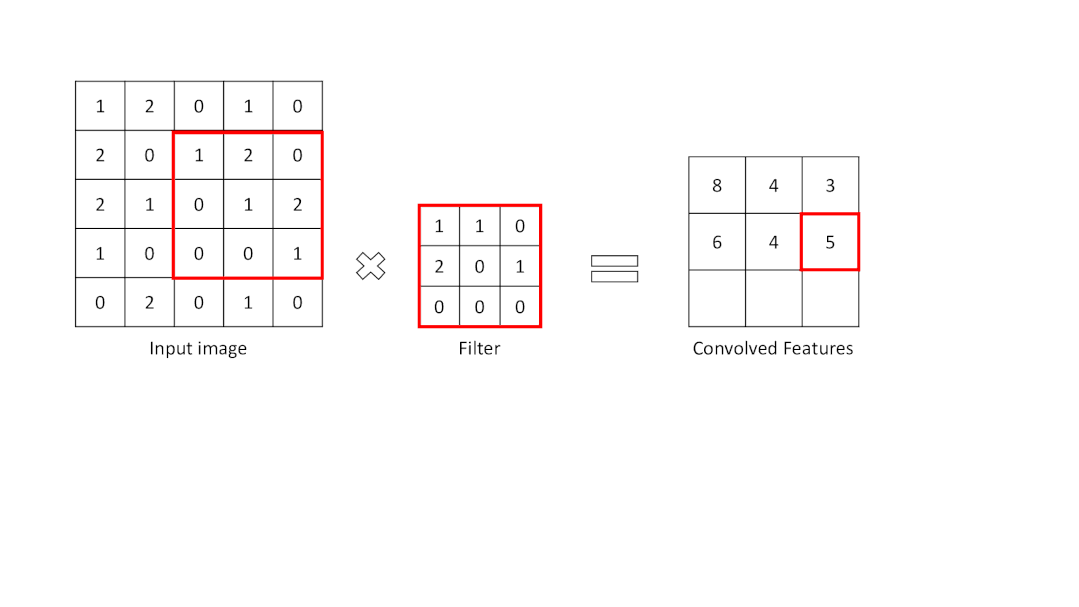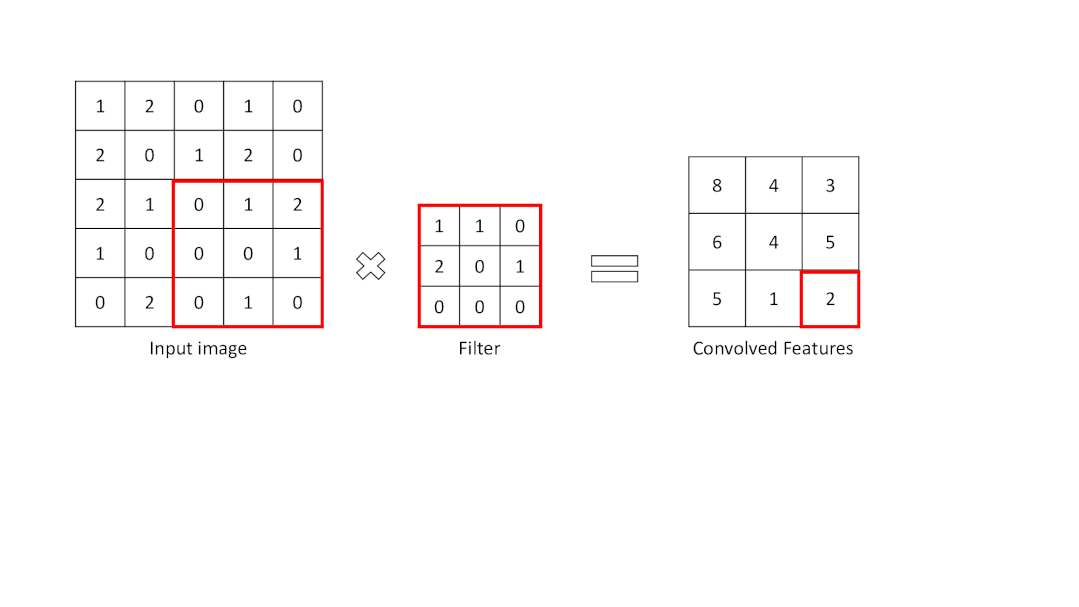
特征图的大小：n-f+1

n = 输入的大小

f = 滤波器的大小

通过不同的过滤器，可以进行不同的操作，如边缘检测、模糊等。

为了进行卷积操作，应指定一个过滤器为一定大小。滤波器在输入图像矩阵上移动，并将数值与滤波器相乘并求和。其结果比输入图像矩阵的大小要小。

总而言之，在CNN中卷积层是最重要的步骤或层。它用于从输入图像矩阵中提取重要特征。一个CNN可以由任意数量的卷积层组成。

非线性层

这一层是在每个卷积层之后添加的，以便为矩阵引入非线性。非线性的引入是为了使输出不受输入的影响或输出与输入不成正比。这种非线性是由激活函数完成的。这是另一篇文章的需要讲述的。

为什么我们需要在神经网络中引入非线性？如果数据没有非线性，那么输入就会直接影响输出，而我们使用多少层都无所谓。结果将是一样的。通过增加非线性的力量，网络的建立可以在数据中找到更多新的和独特的模式。

常用的激活函数有RELU、Tanh等。

padding层

现在你已经明白卷积层有多重要了。一个内核或过滤器被用来提取重要的特征。我提到过，卷积层可以被使用任何次数，而且每次特征图的大小都会减少。我们不需要这样。考虑一个5x5的输入矩阵和一个大小为3x3的过滤器。特征图的大小是5-3+1=3。如果我们再增加一层，那么大小就是1。

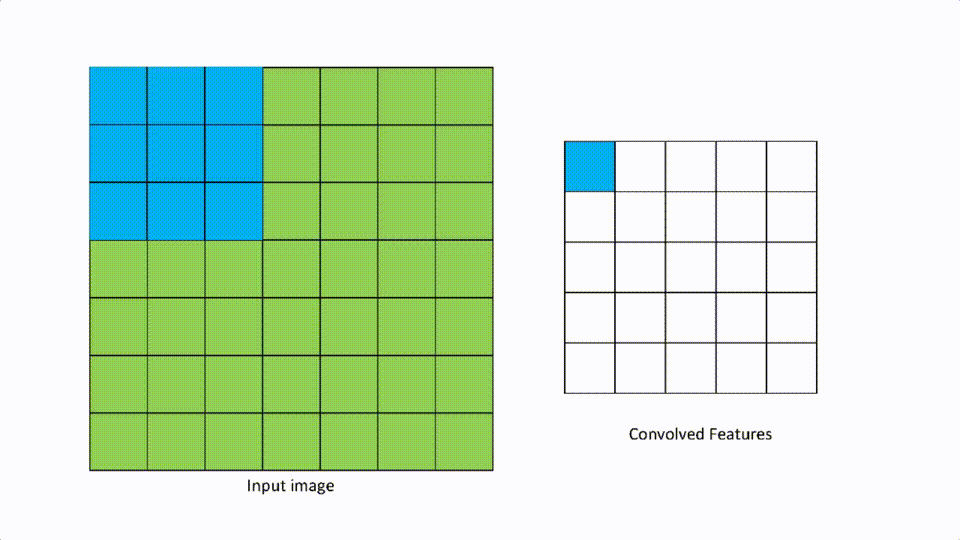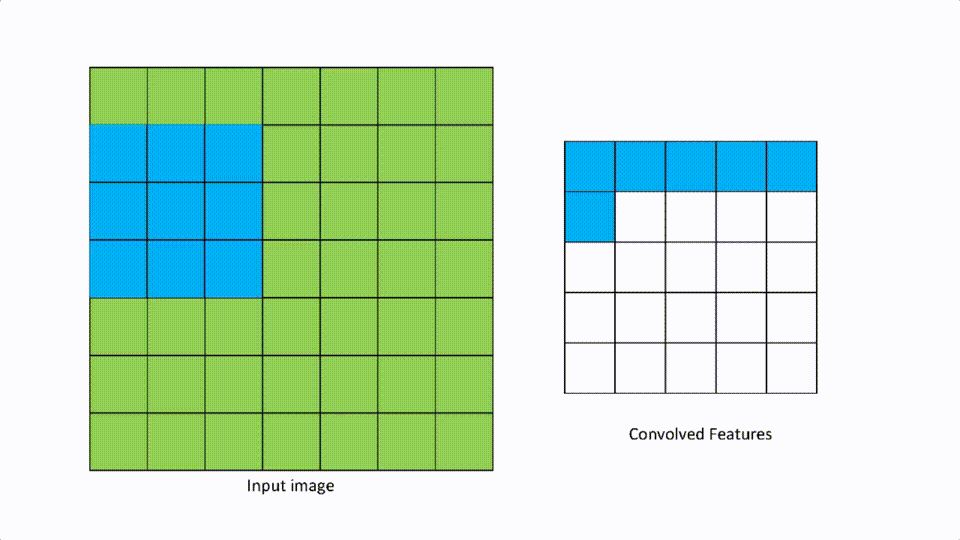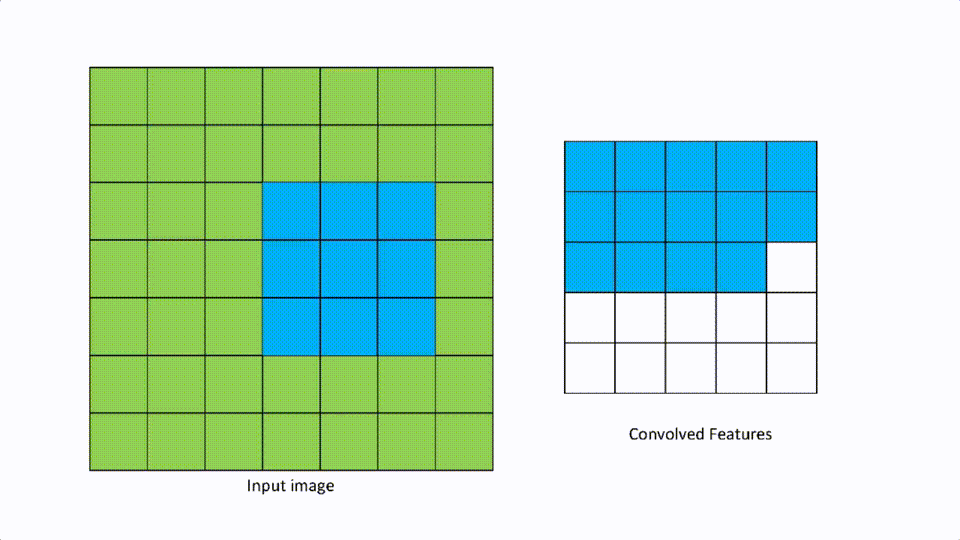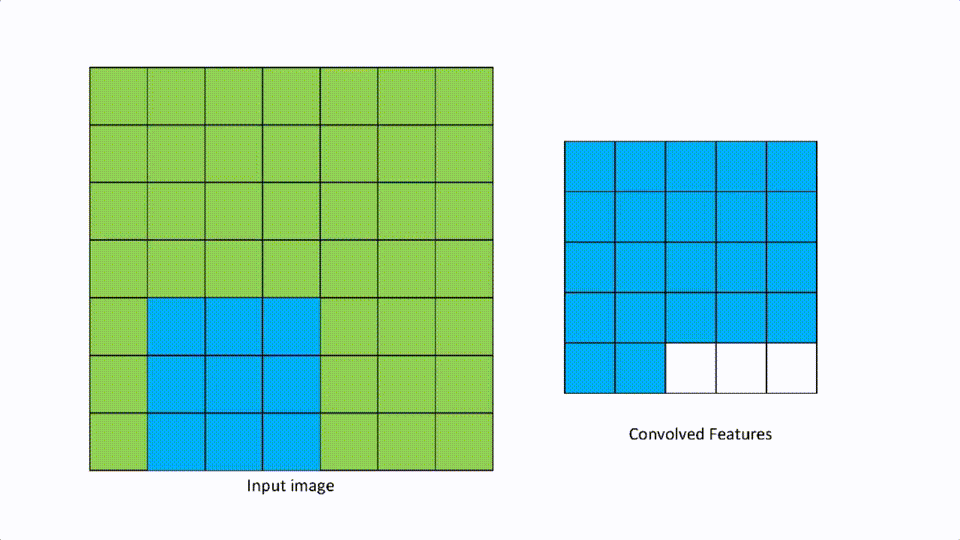
为了使特征图的大小与输入矩阵相同，我们使用填充。让我们进行逆向工程。我们需要一个大小为5的特征图。滤波器的大小是3。从上面的公式来看，n = 5+f-1 = 5+3-1 = 7。

我们需要从一个大小为5的输入矩阵中得到一个大小为7的输入矩阵。我们添加填充物，即在顶部、底部添加一行，在左侧和右侧添加一列，得到一个大小为7x7的矩阵。因此证明了。

padding =n+2p-f+1(p=padding)

如果p=1，那么就有一行和一列，所以这就是为什么我们要加2p，所以我们得到2行和2列。

上述添加的行和列都是用零填充的，称为零填充。

这就是填充物的应用方式。

步幅

我们在卷积层中谈到了过滤器。步幅被定义为在任何方向上移动的像素数，以应用过滤器。如果步幅是[1,1]，那么滤波器在任何方向上每次移动一个像素，如果是[2,2]，那么滤波器在任何方向上移动两个像素。

这个参数主要在有高分辨率的输入图像时有用，然后有更多的像素需要过滤。步幅越大，卷积特征图就越小。

[1,1]看起来就像下面的样子。

一个[2,2]的步幅看起来就像下面那样。

总结一下，步幅是内核或滤波器在输入矩阵上移动的一个值。

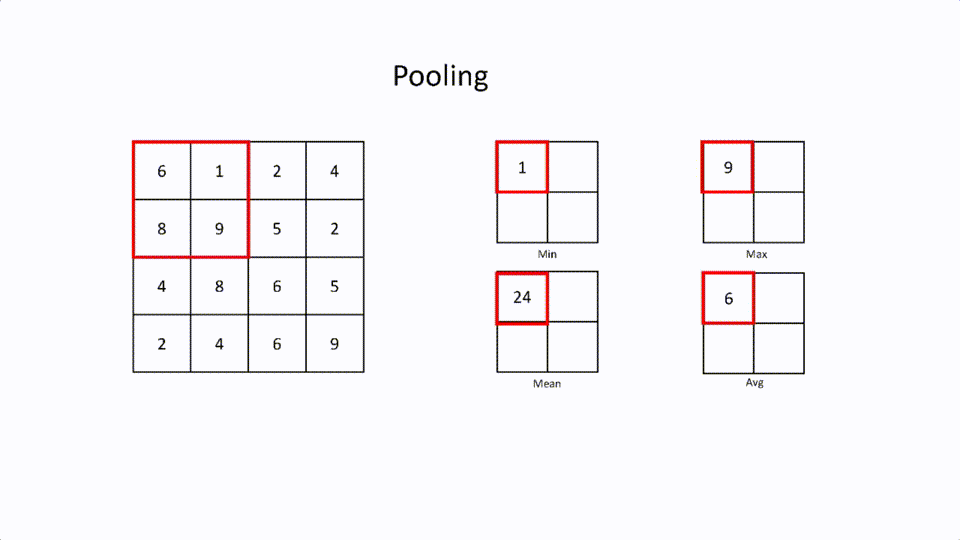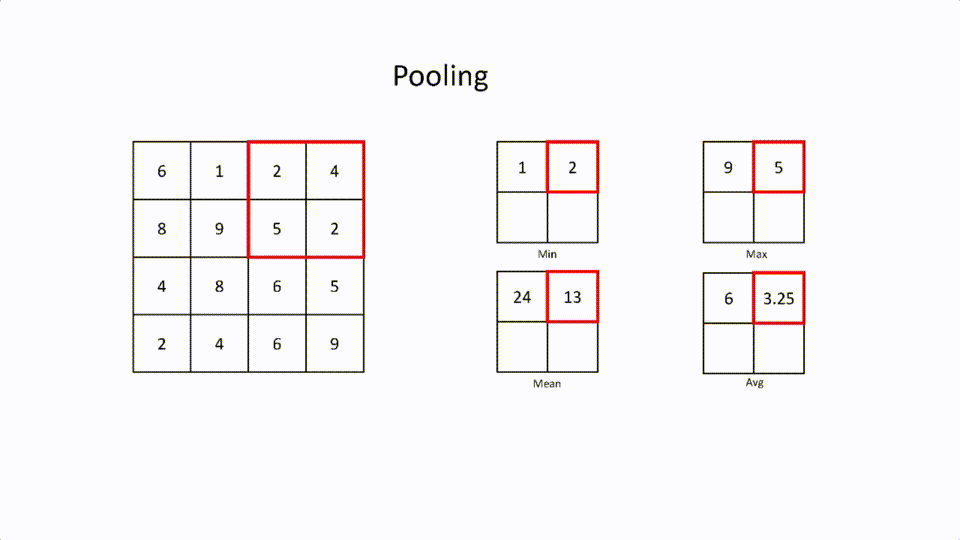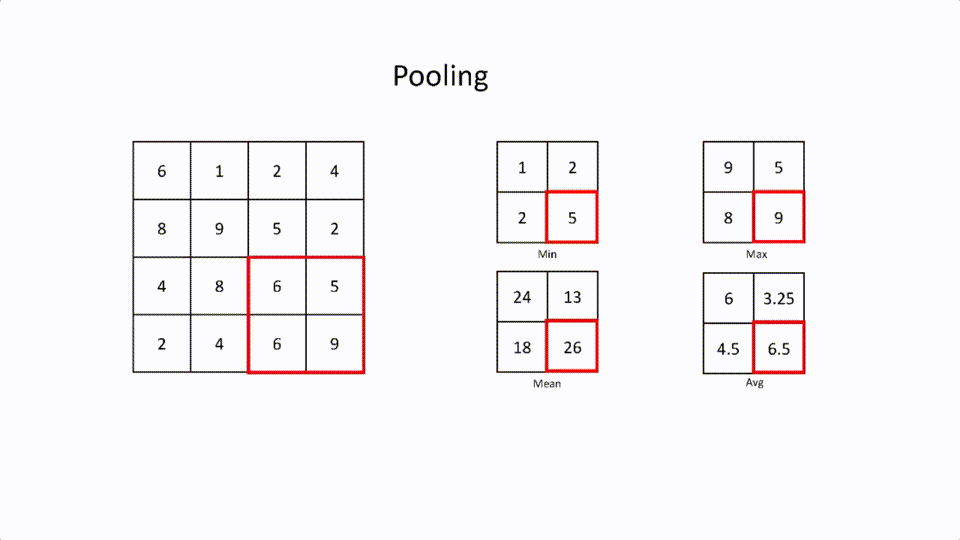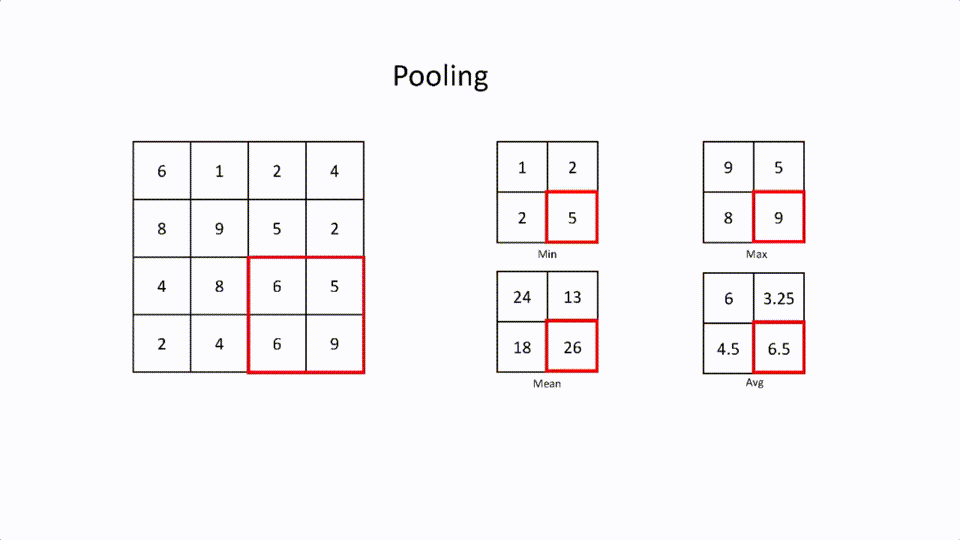
池化层

如果把输入图像推导到1/4就能确定整个图像所描述的内容，那么在处理整个图像时就没有好处。这就是池化的作用。

这是一个通过保留特征来减少大的特征矩阵的层。这就是所谓的空间间隔（spatial spacing）。池化也有一个内核和跨度。有不同类型的空间间距。

• 最大池化。这是在过滤器中选择最大的元素。

• 最小池化。这是在过滤器中选择最小的元素。

• 平均值池化。这是过滤器中所有元素的平均值。

• 平均值池化。这是过滤器中所有元素的平均值。这个池化层主要用于连接卷积层和全连接层。池化层用在卷积层之后的主要原因是为了减少特征图的大小以节省计算资源。

全连接层

所以到目前为止，我们已经获得了一个具有重要特征的矩阵。这个矩阵被扁平化为一个1d向量，并将其送入一个全连接的神经网络。它被称为全连接层，因为每一个神经元都与下一层的每个神经元相连。

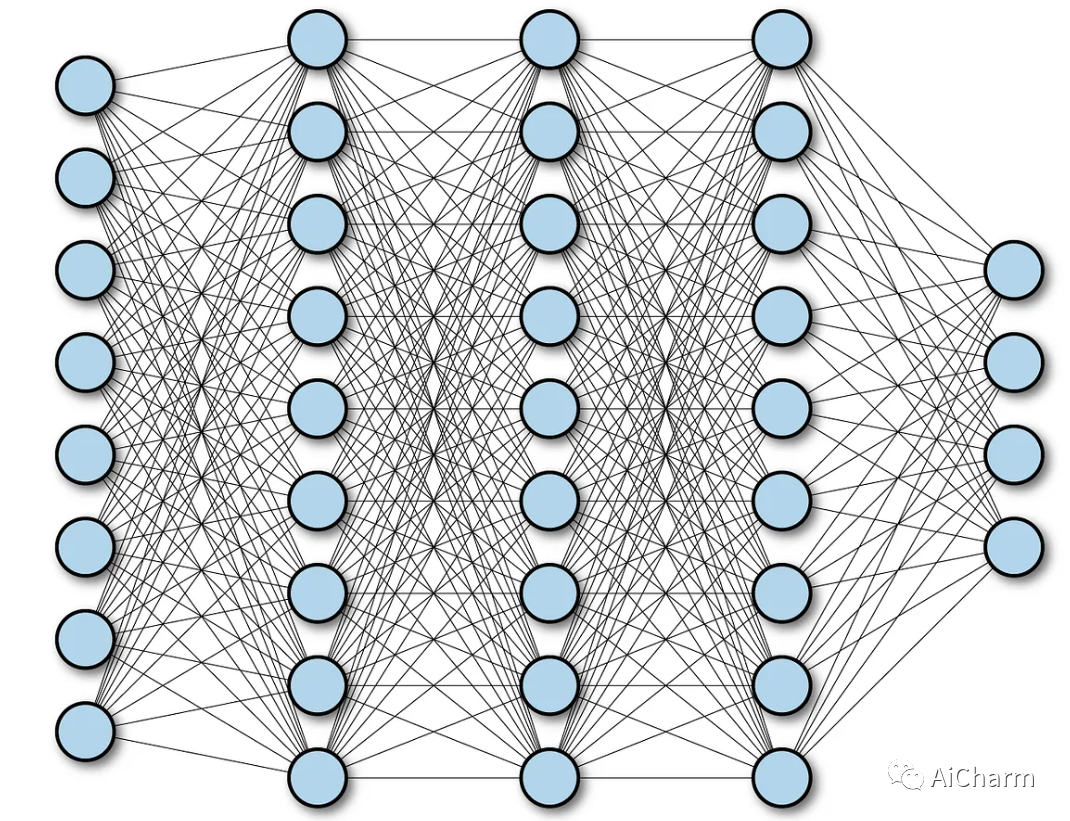
输出层基本上使用softmax激活函数。使用Softmax激活，所以输出的所有概率之和为1。从这里开始，网络作为一个神经网络。

结论

CNN是一个深度学习概念，从图像中提取特征和模式。CNN是一个基本的ANN，但还有两个层，称为卷积层和集合层。