我们之前对树和二叉树有了基本的了解,然后我们进一步对二叉树的性质进行分类。小伙伴们如果有疑问或者感兴趣的可以看一下我之前写的两篇博客。
二叉树(一):二叉树(一)_染柒_GRQ的博客-CSDN博客
二叉树(二):二叉树(二)_染柒_GRQ的博客-CSDN博客
为了巩固之前学的内容,我们先来写两道题目加深映像。

题目
1.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
解析:选A

解析
这里再强调一次,叶子节点就是没有子树的节点,也就是度为0的节点;然后完全二叉树的概念要搞清楚,详见二叉树(二)_染柒_GRQ的博客-CSDN博客
2.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
解析:选B

解析
二叉树的链式存储
其实在二叉树(一)_染柒_GRQ的博客-CSDN博客中我们对链式存储有了初步了解,但是了解得比较浅显,本章内容会跟大家深度了解二叉树中的链式存储。
其实我们之前学的的链表就是链式储存——五分钟入门链表(一)_染柒_GRQ的博客-CSDN博客,我们先来了解一下来自百度的定义,
链式存储:
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的
方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩
子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都
是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
还是老套路,我们先试着把结构图画出来。
法一:
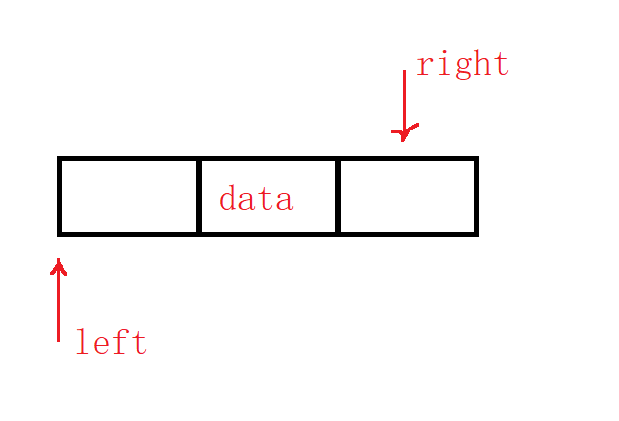
法一
这种方式就是我们在二叉树(一)_染柒_GRQ的博客-CSDN博客中的套路,优点是相当方便,缺点就是不能返回双亲,但是我们要和学单链表与双链表一样,有什么需求就用什么结构,复杂的结构可以应对更加复杂的场景,简单的结构写起来更加方便。
参考文献:五分钟入门链表(一)_染柒_GRQ的博客-CSDN博客
快速入门双链表(上)_染柒_GRQ的博客-CSDN博客
法二:
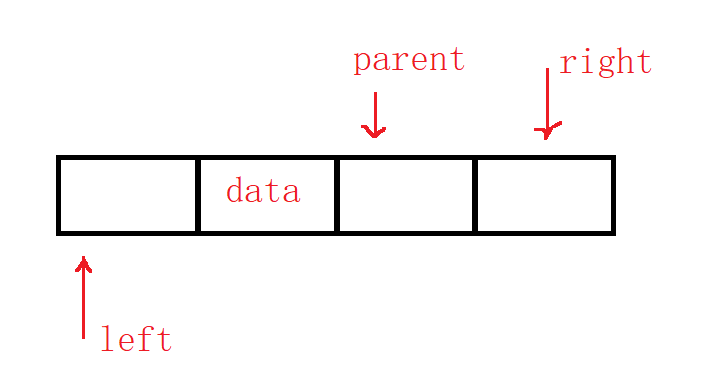
法二
这个结构有了指向双亲的指针可以返回指向双亲,这样便于查找双亲,但是这种结构一般要在平衡树或者红黑树中使用,普通结构一般不用。
那我们就用法一实现代码吧。还是和之前一样。
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTDNode;前序
那么前序实现也差不多。原理:根节点,左子树和右子树。
//前序
void PrevOrder(BTDNode* root)
{
if (root == NULL) {
printf("NULL ");
return;
}
printf("%c ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}中序
那么顺便也写一下中序吧。原理:左子树,根节点和右子树。
//中序
void InOrder(BTDNode* root)
{
if (root == NULL) {
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}后序
我们再来试着实现一下后序。原理:左子树,右子树和根节点。
//后序
void PostOrder(BTDNode* root)
{
if (root == NULL) {
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}计数
我们再试着实现一下计数。
我们可以用递归原理进行。
法一
//法一:
int size = 0;
void TreeSize(BTDNode* root)
{
//为空
if (root == NULL)
{
return;
}
//非空
else
{
++size;
}
TreeSize(root->left);
TreeSize(root->right);
}原理图:
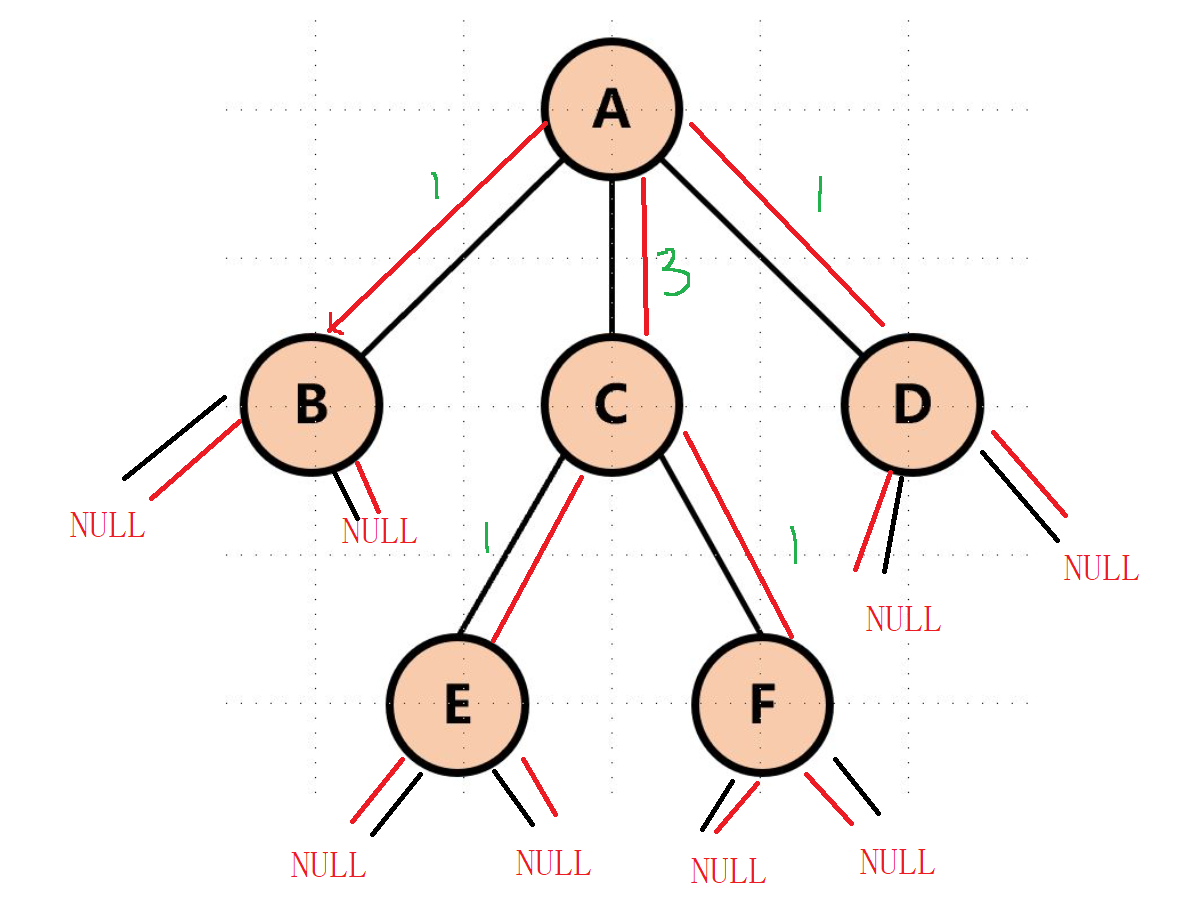
原理图
但是这种全局变量有缺点,我们试想一下,如果是在操作系统中或者多线程任务中,全局变量就很不安全了。
我们试着改一下。
法二
我们是不是可以用指针操作呢?试一下:
//法二:
void TreeSize(BTDNode* root, int* psize)
{
if (root == NULL)
{
return;
}
else
{
++(*psize);
}
TreeSize(root->left, psize);
TreeSize(root->right, psize);
}其实我们还能够更加简便。
法三
我们思考一下,我们计数无非是左边的加上右边的再加上根节点。
原理图;

原理图一
可能这样看不是很清楚,再来修改一下。
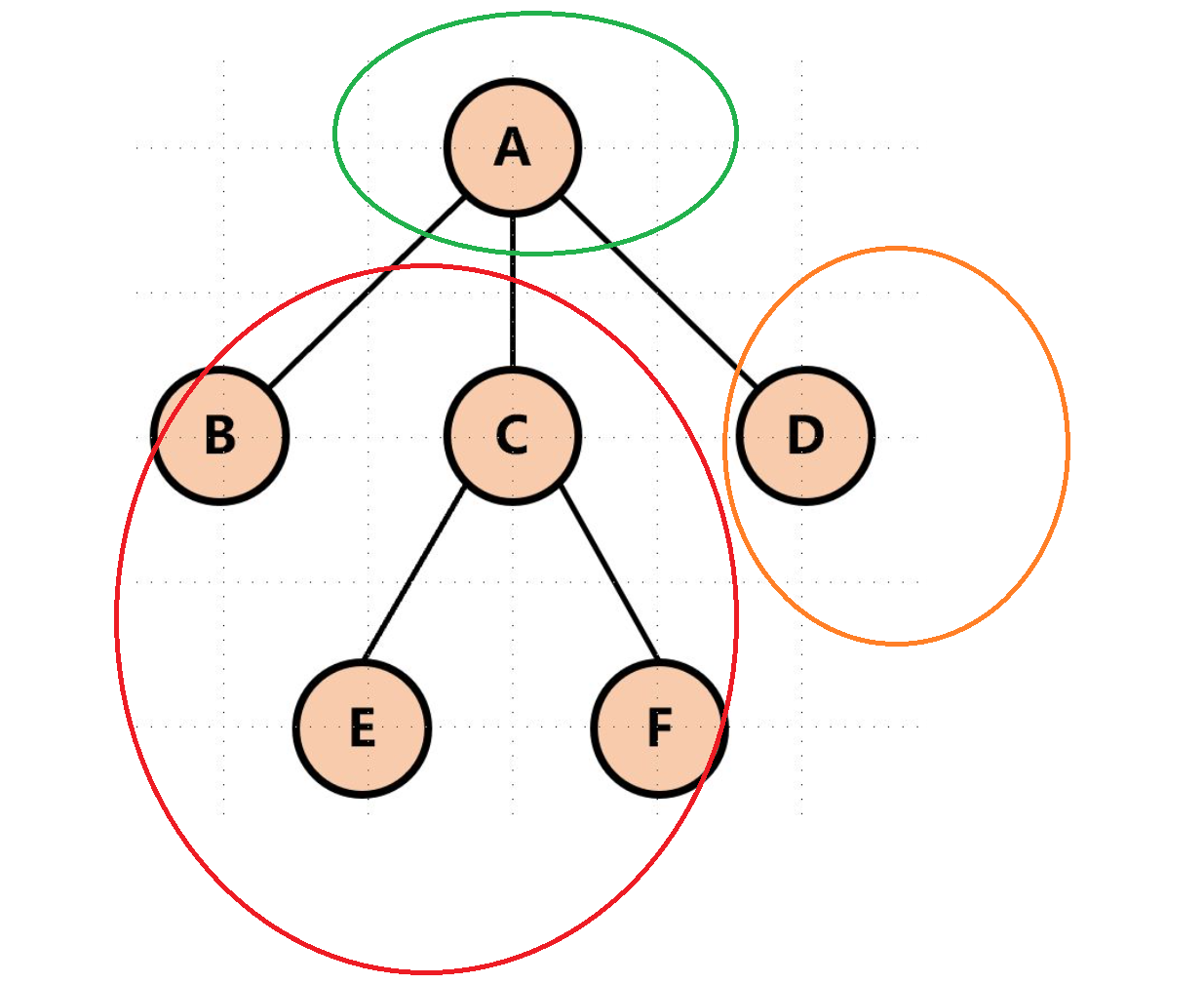
原理图二
我们可以发现这就是三个圈相加。
那么写成代码就是这样:
//法三:
int TreeSize(BTDNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}叶子节点计数
小伙伴们可以自己尝试写一下叶子节点计数。
叶子节点就是度为0或者说没有子树的节点。
转换为代码就是这样:
//变形——叶子节点个数
int TreeLeafSize(BTDNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL
&& root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left)
+ TreeLeafSize(root->right);
}测试
我们用之前的方法来做一个静态的链表。
参考文献:二叉树(一)_染柒_GRQ的博客-CSDN博客
int main()
{
BTDNode* A = (BTDNode*)malloc(sizeof(BTDNode));
A->data = 'A';
A->left = NULL;
A->right = NULL;
BTDNode* B = (BTDNode*)malloc(sizeof(BTDNode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTDNode* C = (BTDNode*)malloc(sizeof(BTDNode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTDNode* D = (BTDNode*)malloc(sizeof(BTDNode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTDNode* E = (BTDNode*)malloc(sizeof(BTDNode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
A->left = B;
A->right = C;
B->left = D;
B->right = E;
return 0;
}我们简单测试一下前序。
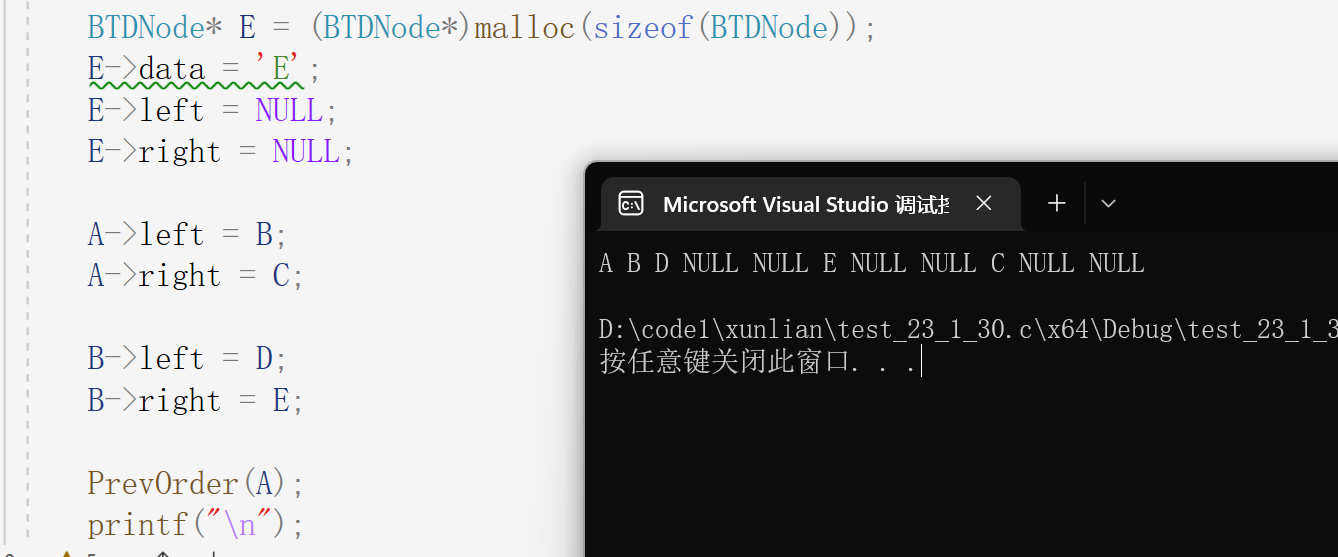
再试一下中序。
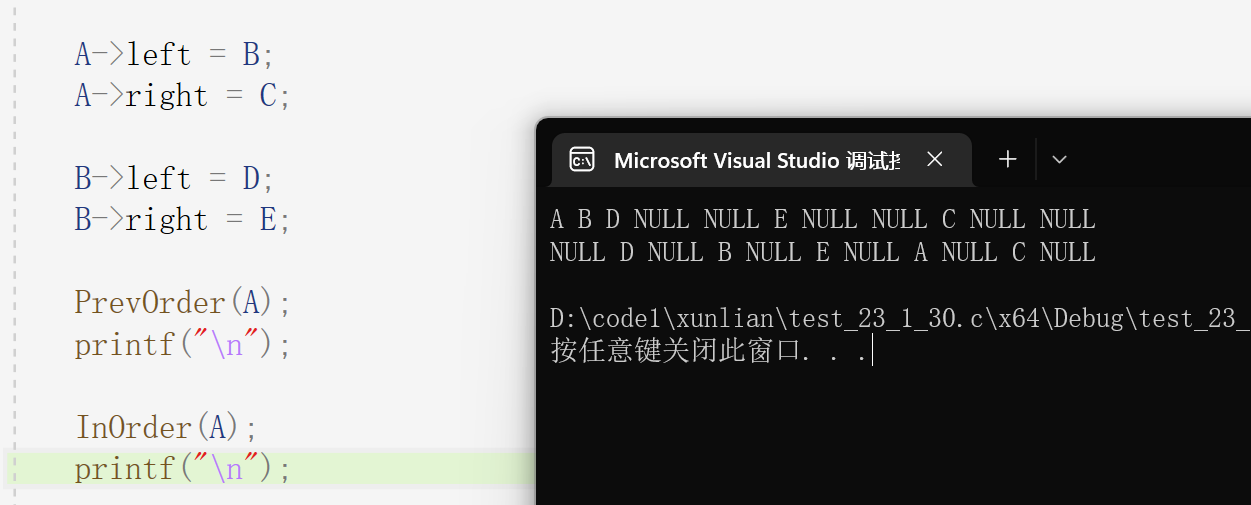
最后再来试一下后序。
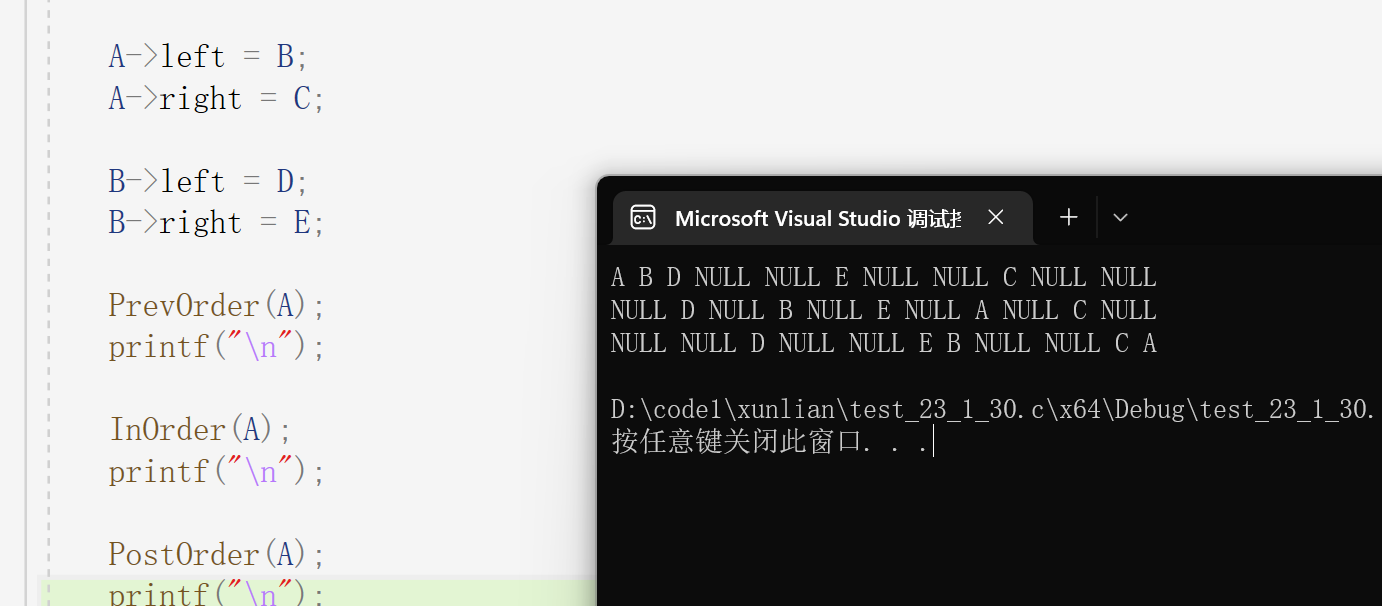
这样三种排序就测试完成了。
我们再来看一下技数的三种方式。
先来看法一:

这里要注意如果要检测别的节点,size要制成0
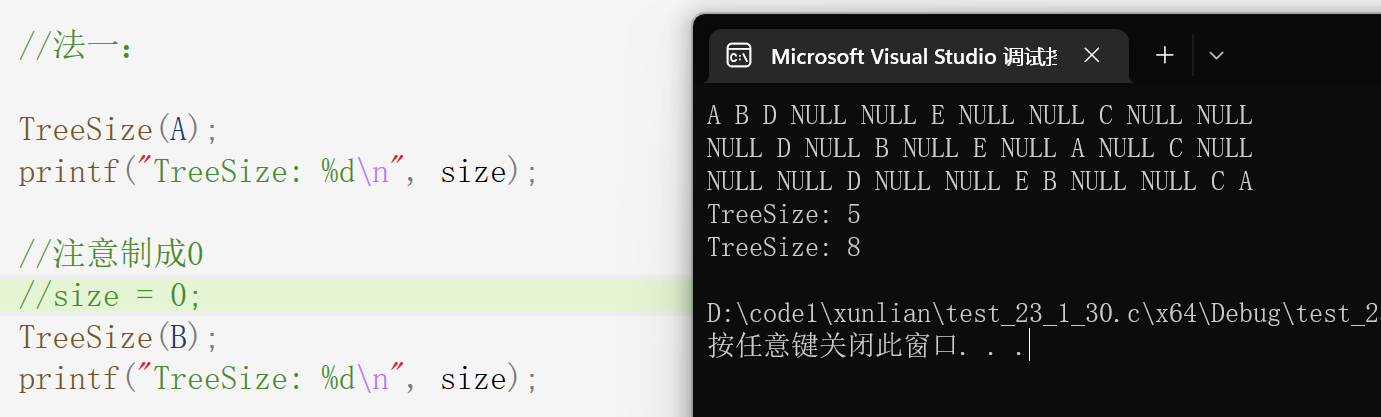
不制成0就会累加。

法二:注意要传指针

法三:

最后再来测试一下叶子节点计数:

这样我们就测试完所以代码了,当然大家如果不熟悉的话也可以写一个测试一个,这样也方便我们更好的写代码,增加自信。
总结
本节复习了前两章的内容,重点是用C语言完善了二叉树的链式储存结构,并对代码进行了测试。




![[思考进阶]05 人与人之间的差距,在于“自律”](https://img-blog.csdnimg.cn/8dba89f8f0a446a1a0df9e53a0666593.png#pic_center)