1. 引言
安全社区已经开发出了一些出色的加密算法,这些算法非常安全,但最终,所有的数据都会被存储在硅和金属中,而入侵者越来越多地会在那里放置监视器来破解密钥。
破解加密密钥通常涉及暴力破解方法或利用实施过程中的缺陷。然而,人们对物理侧信道攻击的兴趣日益浓厚。
侧信道攻击是指:
- 无意中泄露加密信息,如电磁辐射、功耗、电压波动,甚至声音和热量变化。
目前很少有公司保护其设备免受侧信道攻击,尤其是因为这种攻击成本高昂,需要使用复杂的设备进行大量测试。
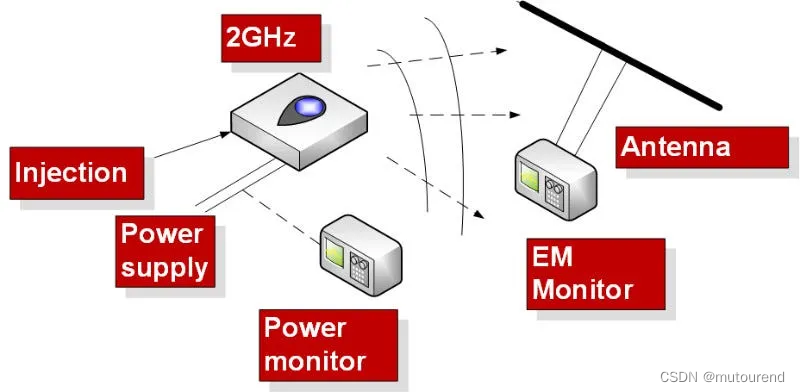
随着设备的速度越来越快,可能会发射越来越多的无线电和电磁 (electromagnetic,EM) 辐射。如:
- 2GHz 处理器的运行频率与 Wi-Fi 信号 (2.4 GHz) 相同,且芯片通常不受无线电波发射保护,这是设备快速运行的自然副产品。由于这些高频,通常很难阻止电磁辐射耦合到附近的电线和其他电路中:
本文重点关注后量子签名方案,如:Dilithium、SPHINCS+ 、FALCON和Raccoon的侧信道攻击问题。
所谓Raccoon: - 为由PQShied开发的,基于Lattice的后量子签名方案。
- 已作为额外签名,提交到NIST PQC竞赛。
- 使用无aborts的Fiat-Shamir方法。而Dilithium则使用的是有aborts的Fiat-Shamir方法。
- 所谓无aborts的Fiat-Shamir方法,是指:支持分布式门限签名,且对侧信道攻击进行了改进。
- 开源代码实现见:https://asecuritysite.com/pqc/raccoon
2. PQC 中的侧通道

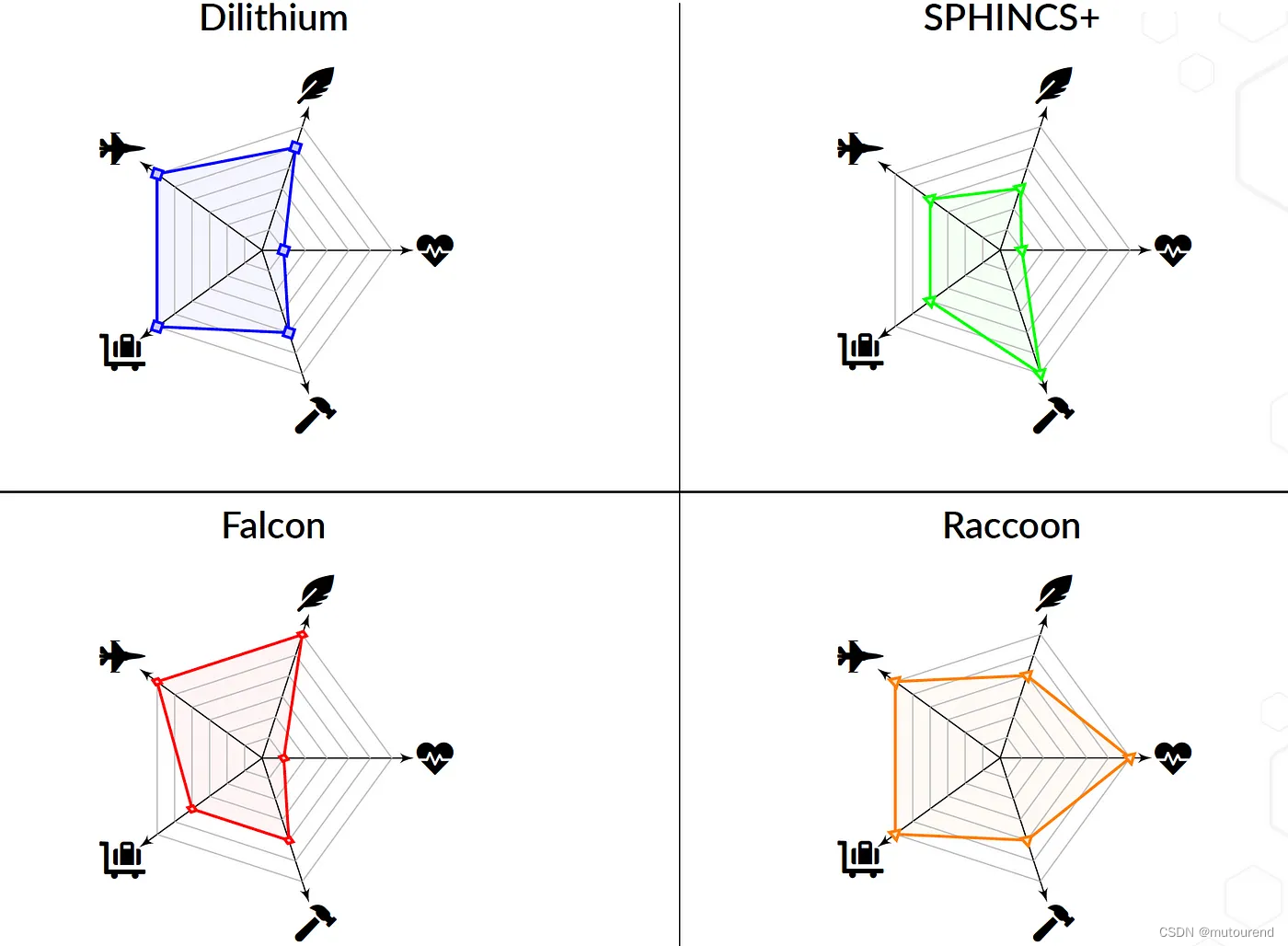
在PQShield团队 Masking-Friendly Signatures and the Design of Raccoon 的精彩演讲中,作者概述了 PQC 签名的三种主要方法(Dilithium、SPHINCS+ 和 FALCON)容易受到侧信道攻击:

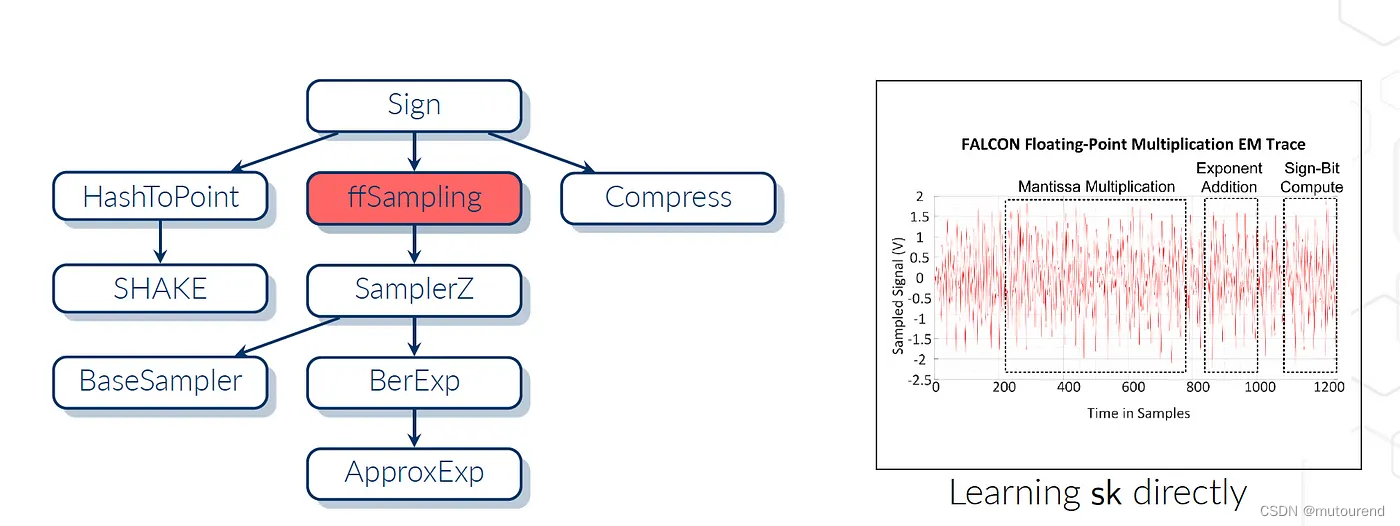
在 FALCON 中,Karabulut 和 Aysu 表明,功耗主要源自签名和私钥(sk)的点积,甚至纯粹是私钥的点积:
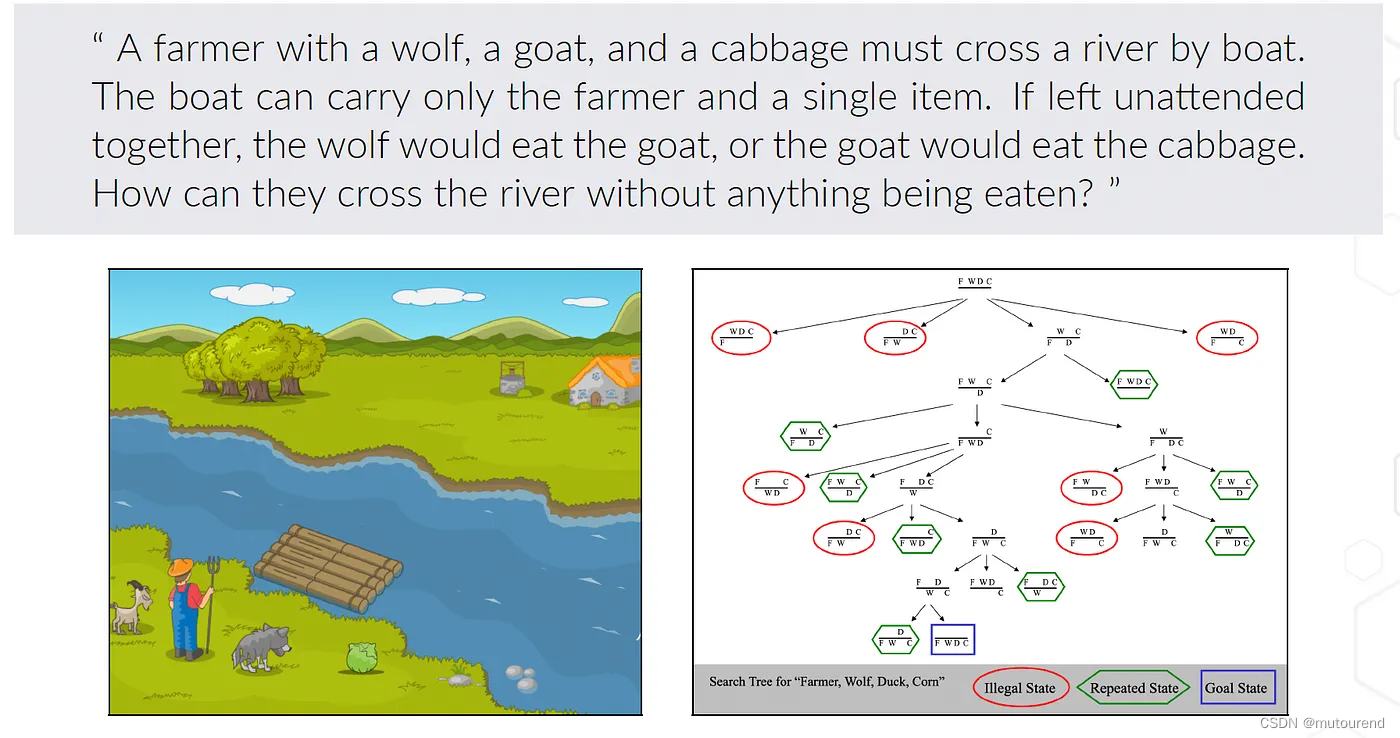
Masking-Friendly Signatures and the Design of Raccoon 作者随后展示了 Dilithium 如何存在侧信道问题,并使用了经典的过河难题:
3. Dilithium后量子签名方案
Dilithium keygen为:
- 从密钥 (
s
k
sk
sk)和误差矩阵 (
e
e
e ) 中推导出公钥 (
v
k
vk
vk ) ,采用经典的 LWE (learning with errors) 方法:
v k = A ⋅ s k + e vk = \mathbf{A}⋅sk + e vk=A⋅sk+e
其中:- A \mathbf{A} A是 k × l k\times l k×l矩阵, t t t是 k k k 个元素的向量。
- 这些都取 ( m o d q \mod q modq ),其中 q q q是素数。
- 验签密钥将是 ( A , v k ) ( \mathbf{A} , vk ) (A,vk),签名密钥是 s k sk sk。
Dilithium签名过程为:
- 采用一个简短的随机秘密(
r
r
r)和消息(
m
s
g
msg
msg),并创建一个挑战承诺(其中
e
′
e'
e′是
e
e
e的一个样本),计算:
w = A ⋅ r + e ′ w = \mathbf{A}⋅r + e' w=A⋅r+e′
c = H a s h ( v k , m s g , w ) c =Hash(vk,msg,w) c=Hash(vk,msg,w)
然后计算:
z = r + c ⋅ s k z = r + c ⋅ sk z=r+c⋅sk- 若z太大,则重试以上计算流程。
- 最后返回 ( w , z ) ( w,z ) (w,z) 作为签名。
这是一个经典的带有aborts的 Fiat-Shamir sigma 方法。该abort用于阻止签名密钥被泄露。
Dilithium验签过程为:
- 首先检查z是否很小。
- 然后计算:
c ′ = H a s h ( v k , m s g , w ) c'=Hash(vk,msg,w) c′=Hash(vk,msg,w) - 然后检查: A ⋅ z ≈ w + c ⋅ v k \mathbf{A} ⋅ z ≈ w + c ⋅ vk A⋅z≈w+c⋅vk
这是有效的,因为error值相对较小:
-
A
⋅
z
=
A
⋅
(
r
+
c
⋅
s
k
)
=
A
⋅
r
+
A
⋅
c
⋅
s
k
≈
w
+
c
⋅
v
k
\mathbf{A} ⋅ z =\mathbf{ A} ⋅ ( r + c ⋅ sk ) = \mathbf{A} ⋅ r + \mathbf{A} ⋅ c ⋅ sk ≈ w + c ⋅ vk
A⋅z=A⋅(r+c⋅sk)=A⋅r+A⋅c⋅sk≈w+c⋅vk
因为 A ⋅ r ≈ A ⋅ r + e ′ \mathbf{A}⋅r ≈ \mathbf{A} ⋅ r+e' A⋅r≈A⋅r+e′且 A ⋅ c ⋅ s k ≈ v k ⋅ c \mathbf{A} ⋅ c ⋅ sk ≈ vk⋅ c A⋅c⋅sk≈vk⋅c。
为了不泄露计算结果,可掩盖该error值或 r。这是通过对均匀分布的error值进行采样来完成的,这可能是一项相当耗时的任务。除此之外,aborts也会减慢签名的生成速度:

4. Raccoon后量子签名方案
Raccoon后量子签名方案:
- 利用了 Lyubashevsky 的签名方法(见Lyubashevsky 2009年论文《Fiat-Shamir with aborts: Applications to lattice and factoring-based signatures》,以及2012年论文《Lattice signatures without trapdoors》),但没有aborts。
Raccoon keygen为:
- 从密钥 (
s
k
sk
sk)和经典 LWE(learning with errors)方法的error 矩阵
e
e
e中得出公钥 (
v
k
vk
vk ):
v k = A ⋅ s k + e vk = \mathbf{A}⋅sk + e vk=A⋅sk+e
其中:- A \mathbf{A} A是 k × l k\times l k×l矩阵, t t t是 k k k 个元素的向量。
- 这些都取 ( m o d q \mod q modq ),其中 q q q是素数。
- 验签密钥为 ( A , v k ) ( A , vk ) (A,vk),签名密钥为 s k sk sk。
Raccoon签名过程为:
- 采用一个简短的随机秘密(
r
r
r)和消息(
m
s
g
msg
msg),并创建一个挑战承诺(其中
e
′
e'
e′是
e
e
e的一个样本):
w = A ⋅ r + e ′ w = \mathbf{A}⋅r + e' w=A⋅r+e′
c = H a s h ( v k , m s g , w ) c = Hash(vk,msg,w) c=Hash(vk,msg,w) - 接下来计算:
z = r + c ⋅ s k z = r + c ⋅ sk z=r+c⋅sk
y = c ⋅ e + e ′ y = c⋅e + e' y=c⋅e+e′ - 那么签名就是 c , z , y c , z , y c,z,y。
Raccoon验签过程为:
- 计算:
w ′ = A ⋅ z + y − c ⋅ v k w'= \mathbf{A} ⋅ z + y − c ⋅ vk w′=A⋅z+y−c⋅vk
c ′ = H a s h ( v k , m s g , w ′ ) c'=Hash( vk , msg , w') c′=Hash(vk,msg,w′) - 然后检查
c
=
c
′
c = c'
c=c′是否成立,若成立则验签通过。
- 这是因为:
w ′ = A ⋅ z + y − c ⋅ v k − A ⋅ ( c ⋅ s k + r ) + c ⋅ e + e ′ + c ⋅ ( A ⋅ s k + e ) = A ⋅ c ⋅ s k + A ⋅ r + c ⋅ e + e ′ − c ⋅ A ⋅ s k − c ⋅ e = A ⋅ r + e = w w'= \mathbf{A} ⋅ z + y − c ⋅ vk − \mathbf{A} ⋅(c ⋅ sk + r)+ c ⋅ e + e'+ c ⋅ (\mathbf{A} ⋅ sk + e)= \mathbf{A} ⋅ c ⋅ sk + \mathbf{A} ⋅ r + c ⋅ e + e'− c⋅ \mathbf{A} ⋅ sk − c ⋅ e = \mathbf{A} ⋅ r + e = w w′=A⋅z+y−c⋅vk−A⋅(c⋅sk+r)+c⋅e+e′+c⋅(A⋅sk+e)=A⋅c⋅sk+A⋅r+c⋅e+e′−c⋅A⋅sk−c⋅e=A⋅r+e=w - 因此 H a s h ( v k , m s g , w ) Hash( vk , msg , w ) Hash(vk,msg,w) 等于 H a s h ( v k , m s g , w ′ ) Hash( vk , msg , w') Hash(vk,msg,w′)。
- 这是因为:
使用 Raccoon,不会在short emphemal secret(r)采样中出现延迟,也不会有aborts:

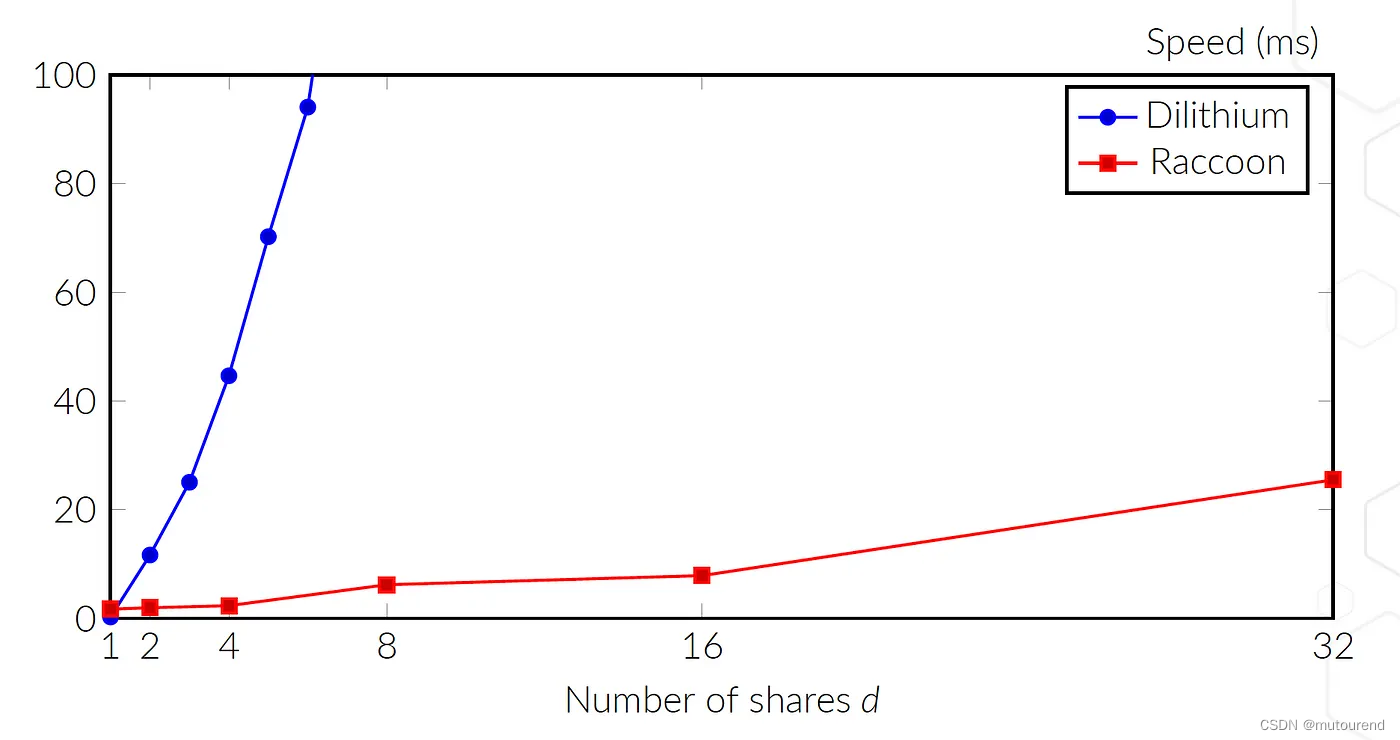
总体而言,将其分成了
d
d
d份,其中 Raccoon 在masking方面的扩展性比 Dilithium 好得多:
5. 结论
PQShield团队slide Masking-Friendly Signatures and the Design of Raccoon的结论部分,可看到 Raccoon 的假设与 Dilithium 类似,且更简单。Raccoon验签(公钥)密钥大小也差不多。不幸的是,签名大小是Dilithium的四倍。若使用masking,Raccoon比其他提议的标准要快得多:

参考资料
[1] Prof Bill Buchanan OBE FRSE 2024年6月博客 Side Channels in Post Quantum Cryptography
[2] PQShield团队slide Masking-Friendly Signatures and the Design of Raccoon
[3] Thomas Prest——PQShield首席密码学研究员博客
[4] 2023年11月20日 2nd Oxford Post-Quantum Cryptography Summit 2023 视频PQC Scheme: Raccoon(相应slide见Raccoon)