一.简单线性回归算法

简单线性回归算法的函数表达式一般为y=kx+b，需要拟合的变量是k和b。

1.导入库和数据集

2.读入数据集并以图表形式展示

分别为x轴和y轴设定标签值为area和price,其中读入的数据集csv文件是在项目的根目录下的文件夹dataset里。打印如图示。

至于数据集大家可以去kaggle上下载，点此跳转即可。

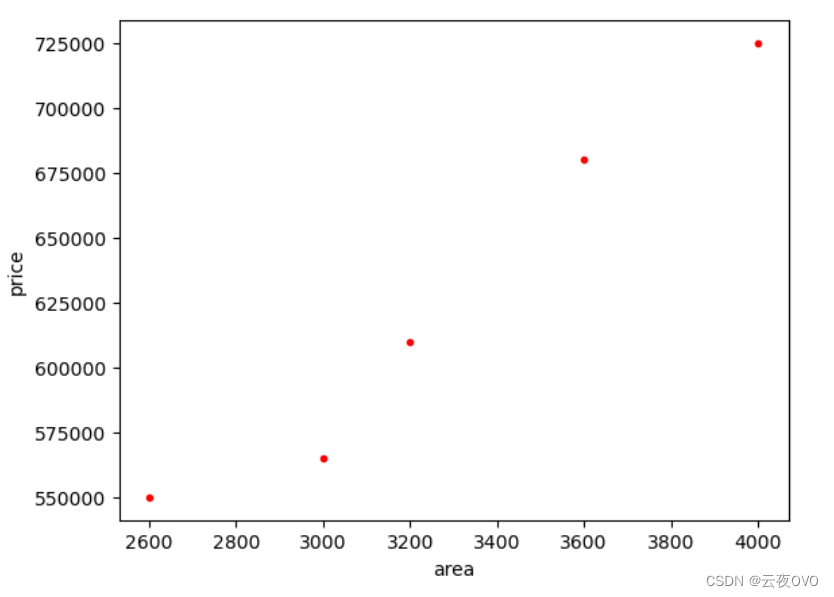
该散点图描述了数据的分布情况。

3.LinearRegression模型引入并进行预测

首先初始化LineatRegression对象ds，再使用pandas库对数据进行处理，得出参数截距和斜率。

然后进行假如我们想知道在房屋面积为：3300平方米时的价格是多少，代码如下：

可以看到房价约为62万。

至此，简单的线性回归模型代码实现已经完成。

二.多元线性回归算法

多元线性回归的方程为y=a*x1+b*x2+c*x3+...+k。其中k参数为偏置值，a,b,...为每个自变量对应的权重。

下面以影响学生学习成绩的部分因素为例探究多元线性回归算法的代码实现。

同样地，

1.导入库和数据集

这里由于数据中所有列不全为数字类型，故需先进行预处理。

打印前十行如下。

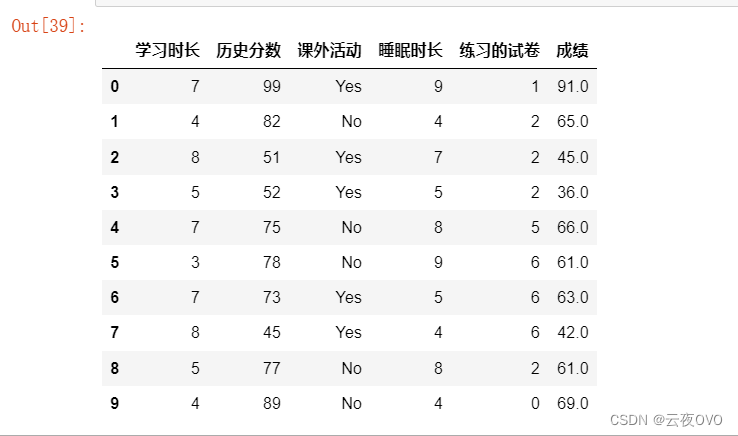
在这里，学习时长，历史分数，课外活动，睡眠时长，练习的试卷为自变量，成绩为因变量。

2.单独处理不为数字类型的列

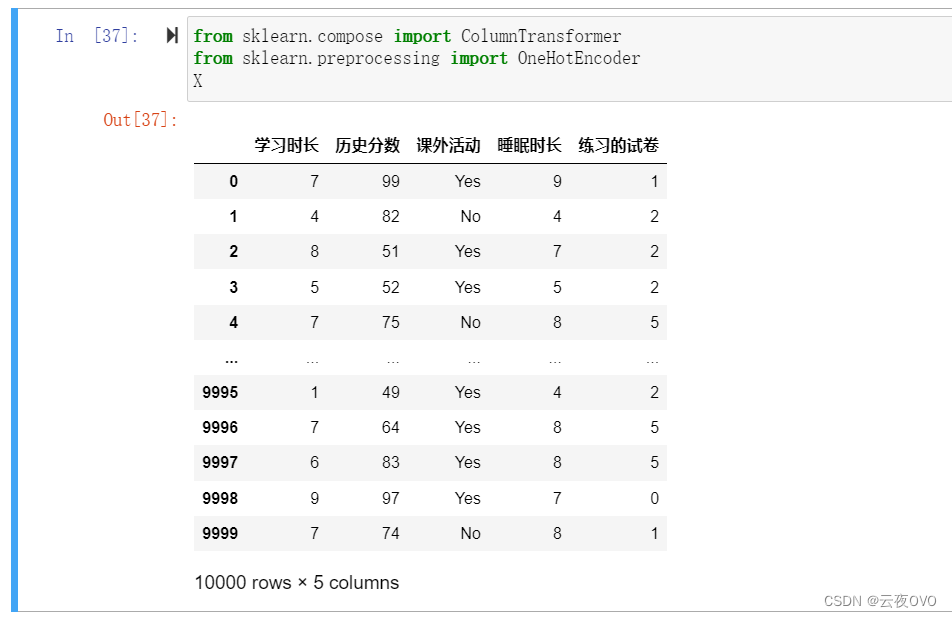
如图所示，从上一步获取到的X我们可以看到，课外活动这一列是字符串类型，故简单将其转换成0，1即可。

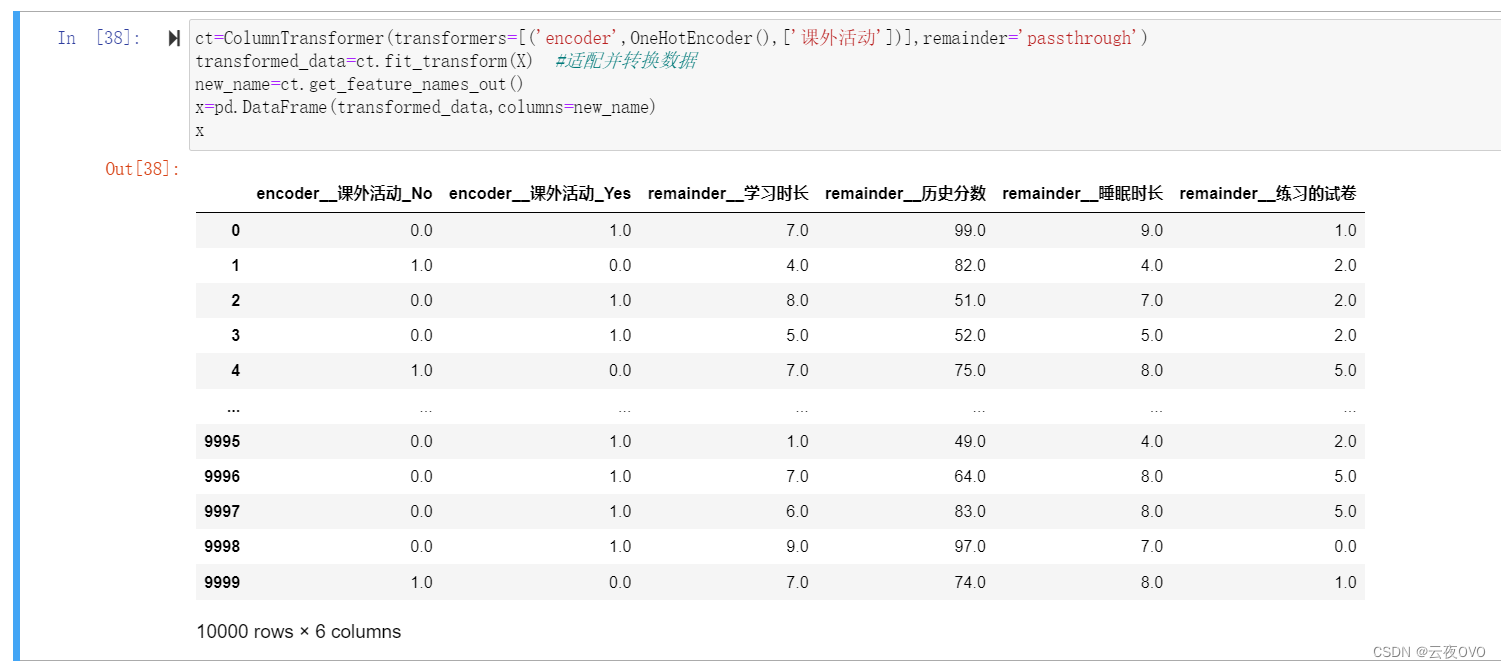
在这里保存原来的x列，将课外活动列单独拆分成两列。

3.将数据集划分为训练集和测试集

这里原来的数据集为10000行X6列，若采用训练集占80%，测试集占20%的比例划分，那么训练集为8000行X7列，测试集为2000行X7列。

打印训练集x如图所示。

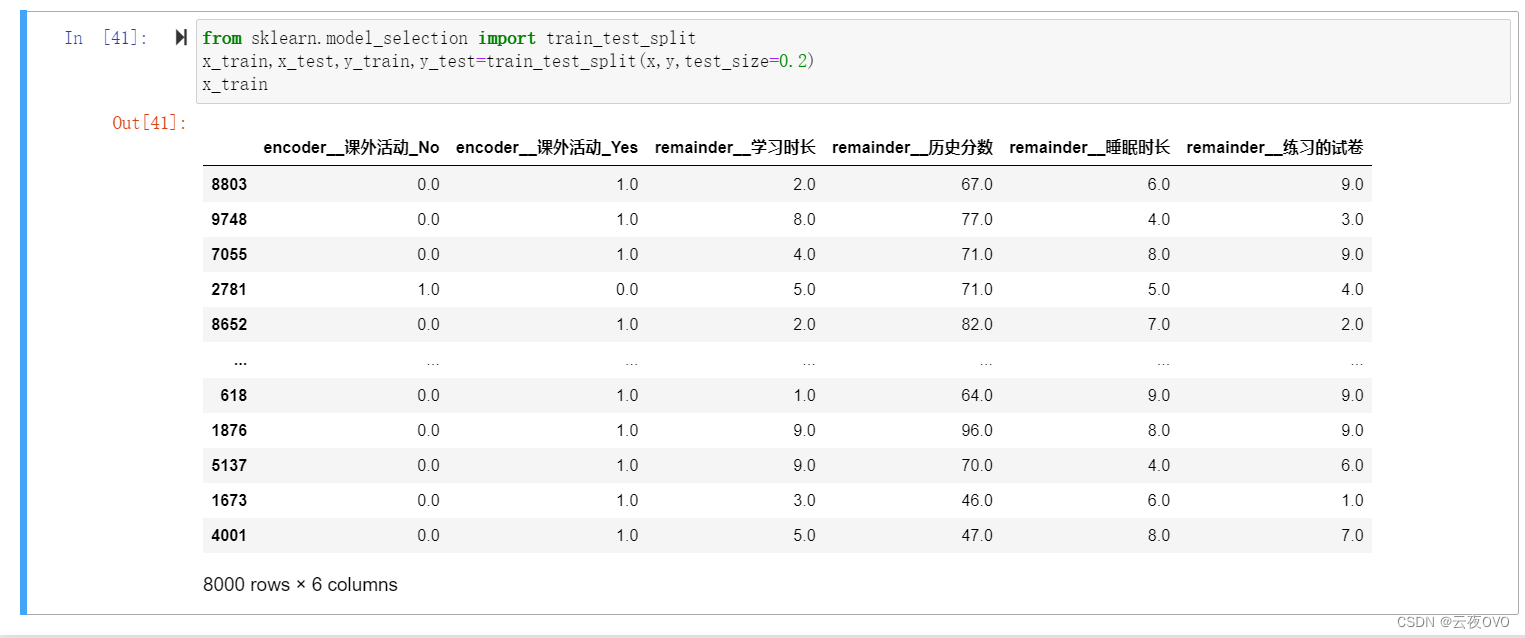
4.模型训练

5.预测结果（基于测试集）

接下来需要在测试集上使用我们训练好的模型去预测结果，观察与实际值的误差。

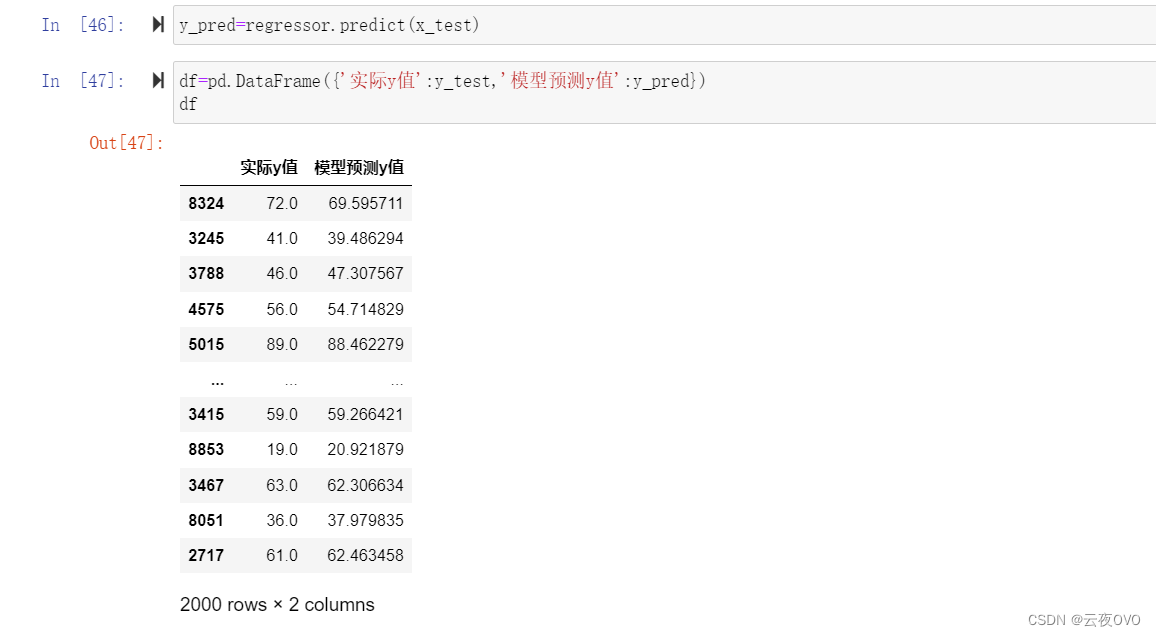
6.模型评估

回归模型的评价指标通常可以是平均绝对误差（MAE）、均方误差（MSE）、均方根误差（RMSE）。本文采用均方根误差指标评价该模型的好坏。

可以看到此时模型的预测精度相对较高，误差相对较小。

至此，线性回归算法代码已完成。后续会逐步更新其他机器学习算法Python代码实战。欢迎各位点赞收藏哈~