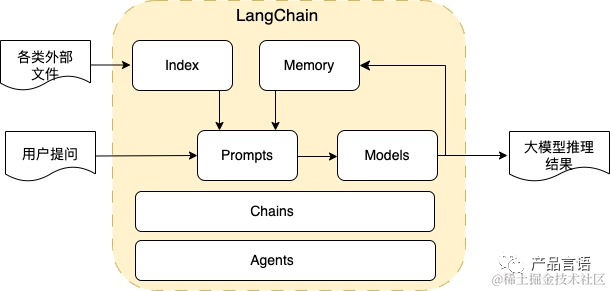
目录
方法一:
方法二:
方法三:
方法四:
没有讲解,但给出了优秀题解
本题链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode)

话不多说,我们直接开始进行本题的思路解析;
首先我们看到这个题是肯定有一种暴力的硬解思路的,
方法一:
那就是将两个vector直接链接起来,然后再排序后,直接返回中间值,这个方法实现起来还是非常容易的,
代码如下:
class Solution { public: double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { size_t n = nums1.size(); size_t m = nums2.size(); if (m == 0) { if (n % 2 == 0) return (nums1[n / 2 - 1] + nums1[n / 2]) / 2.0; else return nums1[n / 2]; } if (n == 0) { if (m % 2 == 0) return (nums2[m / 2 - 1] + nums2[m / 2]) / 2.0; else return nums2[m / 2]; } size_t sum = m + n; int* nums = new int[m + n]; int count = 0, i = 0, j = 0; while (count != sum) { if (i == n) { while (j != m) nums[count++] = nums2[j++]; break; } if (j == m) { while (i != n) nums[count++] = nums1[i++]; break; } if (nums1[i] > nums2[j]) nums[count++] = nums2[j++]; else nums[count++] = nums1[i++]; } if (count % 2 == 0) return (nums[count / 2 - 1] + nums[count / 2]) / 2.0; else return nums[count / 2]; } }; int main() { vector<int> s1; vector<int> s2; s1.push_back(1); s1.push_back(2); s2.push_back(3); s2.push_back(4); s2.push_back(5); s2.push_back(6); Solution s; cout << s.findMedianSortedArrays(s1, s2) << endl; return 0; }首先这个代码是可以编译成功的,
这里也有一个小技巧,如果这个代码是为0,那么证明编译时没有问题的,如果是非0,那么就是编译有问题,还需要修改代码。
但是会过来这个代码再力扣上是运行超时的,因为题目要求的时间复杂度是O(log (m+n))
但是我们的时间复杂度是O(m+n)
空间复杂度也是O(m+n)
方法二:
其实我们的方法一是我们真正的将两个vector真正的链接在了一起,但实际上我们这一步可以省略,我们只需要挨个比较得到第k(假设中位数为第k位)个大的数是多少,那么其实就得到了中位数是多少。其实这一题方便了一点,题目给的数组是已有序的,所以我们挨个比较就行
开始我们写一个循环,这个循环我们的目的就是找到中位数所对应的下标是多少,如果找到了,那么就返回他的下标值,还没找到,那么就继续。但是这样来说,对偶数和奇数的分类会很麻烦。当其中一个数组遍历完后,还要分好几种情况进行另类判断另一个数组,这样想起来都麻烦。
然而要进行优化,那么我们就需要找到要进行优化的部分,那么就是考虑对偶与奇的情况不分开讨论,进行合并考虑,对于此情况我们可以在另定义两个变量left与right分别保存左操作数与右操作数。
假设合并的数组长度为len,那么无论对应偶还是奇,我们只需要遍历前 len/2+1 个数就可以(如果是偶数,我们需要知道第 len/2和 len/2+1 个数,也是需要遍历 len/2+1 次。所以遍历的话,奇数和偶数都是 len/2+1 次。)
返回的left与right我们要做到如果是奇,那么只需要right,如果是偶,因为left不等于right,所以返回两个数的平均数;所以我们在for循环里应该保证依次循环过后left与right差一个位,所以我们要先在循环开始将right的值赋给left,后进行调整right。
然后写出大致框架:
如果nums1[i]<nums2[i],那么就将nums1[i]赋值给right,反之nums2[i];
我们在调整right的时候首先要考虑的就是nums是否越界,所以我需要先判断是否越界,同理考虑了nums1也需要考虑nums2;
所以填充完代码如下:
class Solution { public: double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { int m = nums1.size(); int n = nums2.size(); int len = m + n; int left = -1, right = -1; int aStart = 0, bStart = 0; for (int i = 0; i <= len / 2; i++) { left = right; //调整right if (aStart < m && (bStart >= n || nums1[aStart] < nums2[bStart])) { right = nums1[aStart++]; } else { right = nums2[bStart++]; } } if ((len % 2) == 0) return (left + right) / 2.0; else return right; } }; int main() { vector<int> s1; vector<int> s2; s1.push_back(1); s1.push_back(2); s2.push_back(3); s2.push_back(4); s2.push_back(5); s2.push_back(6); Solution s; cout << s.findMedianSortedArrays(s1, s2) << endl; return 0; }
运行起来是正确的,但依然在力扣上是不行的,还是运行超时;
时间复杂度是:遍历了m+n/2+1个数,但时间复杂度还是O(m+n);
方法三:
我第一眼看到这个题的时候,首先想到的就是二分查找,然后就想到了分别对两个数组进行二分,但是如果nums2全都大于num1那么这样就不行,然后我在看了别人的题解后然后理解了理解,就大为震撼,妙,但是题解是java的然后我自己又写了写修改了好几次终于写出来了。
方法二中,我们一次遍历就相当于去掉不可能是中位数的一个值,也就是一个一个排除。由于数列是有序的,其实我们完全可以一半儿一半儿的排除。假设我们要找第 k 小数,我们可以每次循环排除掉 k/2 个数。方法三其实与方法二同理,也是主要找到第k个数是多少。
下面我们看一个例子


此时3=3
然后我们需要将两个数组的第 k/2 个数进行比较 ,然后将小的那个数组前k/2个数舍弃,对于方便处理,我们设定如果两个数相等,目前我们先优先删除第二个数组删除;(后面代码是是先有限舍弃第一个数组,这里是为了避开特殊情况)
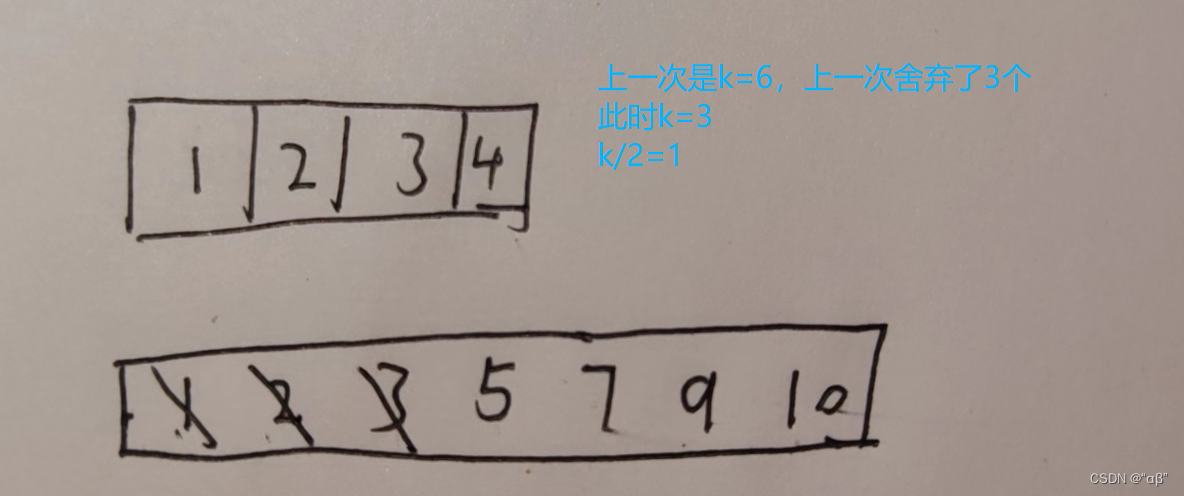

此时1<5
这次舍弃num1 的 k/2 个数;


此时2<5
同理,继续舍弃nums1,舍弃 k/2 个数
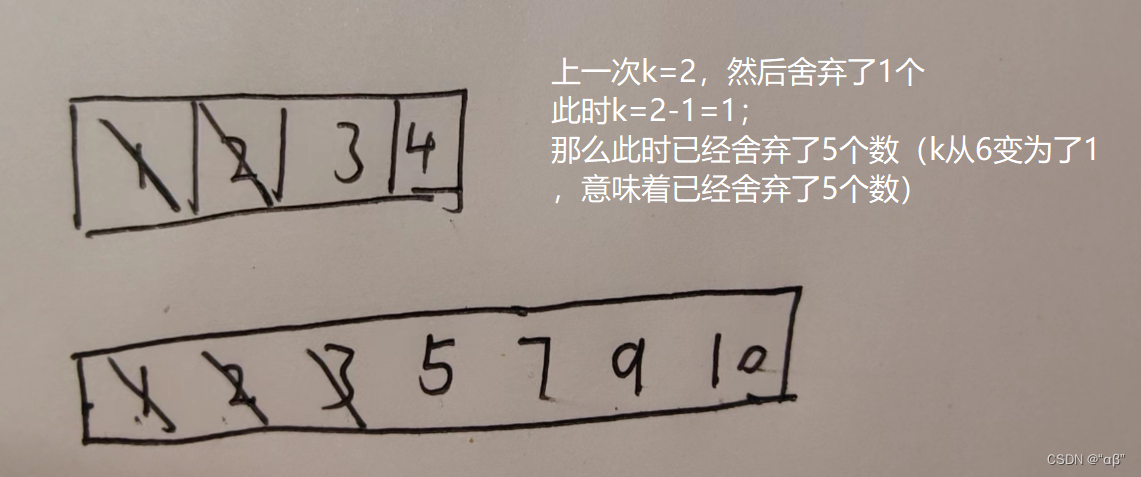
 这时候3<5;这时候3就为第6大的数,就是中位数。
这时候3<5;这时候3就为第6大的数,就是中位数。
这个方法是不是很妙呢?
然后我们就刷刷的写,然后突然就有一个案例不通过,那就是
如果按照上面的方法进行按照步骤进行梳理,那么就会发现第一步的时候就会卡住,因为第一步我么要进行舍弃的数的个数就已经超出了nums1的长度,直接会越界,那么这时候我们就需要进行特殊处理,如果舍弃个数大于剩余长度,那么就舍弃剩余长度。
思路全部梳理完后,如果对递归熟悉的话,那么就完全可以写出来,思路难想,但是代码实现还是比较简单的。(特殊案例我也进行处理了,后面会进行特别分析)
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size();
int m = nums2.size();
int left = (n + m + 1) / 2;
int right = (n + m + 2) / 2;
return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;
}
int getKth(vector<int>& nums1, int start1, int end1, vector<int>& nums2, int start2, int end2, int k)
{
//舍弃k/2个
//结束条件k==1
int len1 = end1 - start1 + 1;
int len2 = end2 - start2 + 1;
//让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1
if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
//还存在一种情况,就是k不为1的情况下,但len1已经等于0
if (len1 == 0)
return nums2[start2 + k - 1];
if (k == 1)
return min(nums1[start1], nums2[start2]);
int i = start1 + min(len1, k / 2) - 1;
int j = start2 + min(len2, k / 2) - 1;
if (nums1[i] > nums2[j])
{
return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
}
else
{
return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
}
}
};到此我们就出来了第一种在力扣上通过的代码;
然后进行特别分析
1:
这一步也是跟方法二同样的找到求中位数的操作数第left是第几个,right是第几个;与之不同的就是奇的情况下left=right,偶的情况下left+1=right;
2:
此案例对应的也就是
在求right的时候k=7;先舍弃k/2=3个
此时k=4;
然后再舍弃的话num1已经没有了但是k=4-2=2;还不为1;如果返回的还要再舍弃的话,就会报错越界;
所以要加特殊情况处理
3: 
这一步也是为了对应2,方便,如果没有这个,那么就有可能len2先空的情况,所以这一步避免了分类讨论;
最后再展示一边代码:
class Solution { public: double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { int n = nums1.size(); int m = nums2.size(); int left = (n + m + 1) / 2; int right = (n + m + 2) / 2; return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5; } int getKth(vector<int>& nums1, int start1, int end1, vector<int>& nums2, int start2, int end2, int k) { //舍弃k/2个 //结束条件k==1 int len1 = end1 - start1 + 1; int len2 = end2 - start2 + 1; //让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1 if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k); //还存在一种情况,就是k不为1的情况下,但len1已经等于0 if (len1 == 0) { return nums2[start2 + k - 1]; } if (k == 1) return min(nums1[start1], nums2[start2]); int i = start1 + min(len1, k / 2) - 1; int j = start2 + min(len2, k / 2) - 1; if (nums1[i] > nums2[j]) { return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1)); } else { return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1)); } } };运行成功
时间复杂度是
O(log (m+n))。符合要求
方法四:
但是这个方法三还是效率不是很高, 
其实还有一种更牛的方法,但本人看了看看不明白,运用到了统计学;本人还没有学统计学,能看明白一点,但是还是看清楚;
我看了题解有两种一个数官方一个是别的作者大佬写的;本人推荐大佬,官方直接给了题目解释,没有给知识补充;
4. 寻找两个正序数组的中位数 - 力扣(LeetCode)
为了方便这里给出了全部官方截图:

最后这个题就已经完全讲解完了,第一次完全写完力扣困难题,总的来说是很难,但不至于一点思路也没有,而且写的过程中思考是很多的,还是比简单题写起来吃力。有能力还是多写困难题;









![[知识点篇]《计算机组成原理》之计算机系统概述](https://img-blog.csdnimg.cn/direct/29dcb49998074fbdaec6cbfef7272d26.png)