Sparse4D: Multi-view 3D Object Detection with Sparse Spatial-Temporal Fusion

单位：地平线

GitHub：https://github.com/HorizonRobotics/Sparse4D

论文：https://arxiv.org/abs/2211.10581

时间：2022-11

找博主项目讨论方式：wx：DL_xifen

讨论QQ群：345458279

摘要

• 基于BEV的检测方法在多视角3D检测任务中取得了很好的效果，基于稀疏方法的一直落后，但并不是没有优点的。
• 本文提出了一个迭代优化锚框，通过稀疏采样的方法，融合时空特征。叫做sparse 4D
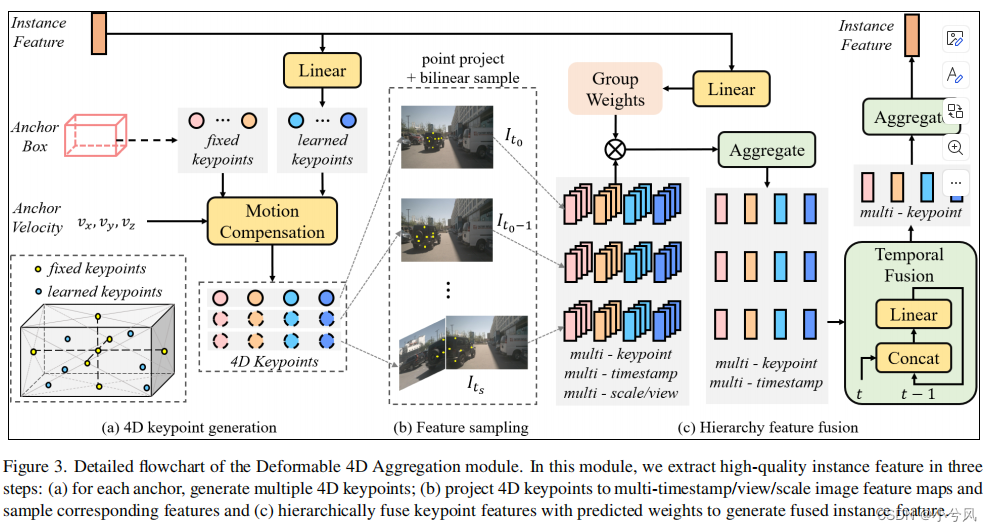
  • （1）：Sparse 4D Sampling：对每一个3D锚框，将多个采样4D关键点映射到多视角，多尺度，多时间戳上的图片去采集相应特征。
  • （2）：Hierarchy Feature Fusion：将不同视图/尺度、不同时间戳和不同关键点的采样特征分层融合，生成高质量的实例特征
  • （3）：从而，Sparse 4D是高效，不依赖稠密视角转换，有利于边缘设备的部署。
• 本文引入了实例级-深度重载模块，缓解3D-到2D映射的病态问题。
• 本文的方法超越了所有基于稀疏感知的方法和一些基于BEV的方法在nuScenes数据集上。

引言

1. 多视角的3D感知是自动驾驶系统的关键一环，部署成本低的优势。
2. 相较于LiDAR, 相机可以为远距离目标提供视觉线索
3. 但是，相机没有深度信息，这就导致了从2d图像中感知3d目标，是一个长期的病态问题。
4. 如何融合多视角信息，解决3D感知任务，是一个有意思的问题
5. 现在有2种主流方式，一种是基于bev的方法，一种是基于sparse的方法。

---

6. BEV的方法就是将多个视图特征转到统一的BEV空间，实现一个比较好的表现效果
7. 但是BEV方法也有一些劣势
   • 图像特征转BEV需要稠密的特征采样和重组，计算复杂其计算量大
   • 最大感知范围局限于BEV特征图的大小，难以权衡效率，精度，速度。
   • 将特征压缩到BEV会丢失一些纹理信息，导致如符号检测就不能实现了。

---

8. 不同于BEV方法，sparse方法不要求稠密视角转换模块，而是直接3D特征采样，然后优化锚框，从而能够避免上述问题。
9. 其中最具代表性是的DETR3D，但是他局限于每一个query一个采样点
10. SRCN3D 利用RoI-Align采样多视角特征, 但是不够高效同时也不能对其不同视角的特征
11. 此外，现有的sparse 3D 并未发挥出时序信息的优势，相较于BEV方法，在精度上有巨大的gap

---

12. 本文提出了一个Sparse4D 解决上述问题
13. 每一个锚框采用多个采样点，相较于单采样点和RoI-Align采样具有2点优势：
    1. 能够提取更加丰富的特征信息
    2. 便于扩展到时间维度，作为4D的采样点，提取时序信息
14. Sparse4D首先对每个关键点执行多时间戳、多视图和多尺度的操作。
15. 然后，这些采样特征通过分层融合模块生成高质量的实例特征，用于3D边界框的优化
16. 此外，为了缓解基于相机的3D检测深度病态解的问题，提高感知性能，添加了一个实例级深度重权模块，用于预测深度信息(该模块以稀疏的方式进行训练，没有额外的激光雷达点云监督)。
17. 主要贡献如下：
    1. 第一个具有时间上下文融合的稀疏多视角3D检测算法，它可以有效地对齐空间和时间视觉信息，从而实现精确的3D检测。
    2. 提出了一个 deformable 4D aggregation module 能够灵活计算和采样不同维度的信息
    3. 提出了一个 depth reweight module 缓解3D感知中的位置病态问题
    4. 在 nuScenes数据集上超于了所有sparse方法，以及超越了需要BEV方法。

相关工作

稀疏目标检测

1. 早期的目标检测任务使用密集输出，再使用NMS进行过滤
2. DETR是一个新的检测范式，作为集合预测，利用transformer直接稀疏预测结果。
3. DETR采用了query与图像之间的交叉注意力，导致计算量大并且收敛困难。
4. 由于使用了全局注意力，DETR也不能认为是一种纯的稀疏方法
5. Deformable DETR修改了DETR，提出了基于参考点的局部注意力，能够加速收敛和减少计算量
6. Sparse R-CNN提出了一种anchor 稀疏的方案，基于 region proposal，网络结构简单有效。展示了稀疏检测的有效性和优越性
7. 3D检测作为2D检测的扩展，也有许多稀疏的检测网络MoNoDETR,DETR3D, Sparse R-CNN3D, SimMOD

单目的3D目标检测

1. 单张图片实现3D检测更加具有挑战性
2. FCOS3D，SMOKE是基于2阶段的2D目标检测器，通过卷积神经网络直接回归深度信息
3. [31,40，43]利用单目的深度估计，将图像转为伪点云，再进行3D目标检测。
4. OFT and CaDDN 利用视角变换模块，将视角从图像转为BEV空间，然后完成3D的检测。
5. OFT 是将利用3D到2D的映射关系完成的变换，而CaDDN是2D到3D的映射。(更加像一种伪点云的方法)

多视角的3D目标检测

1. 稠密方法是多视图三维检测的主要研究方向，它利用密集的特征向量进行视图变换、特征融合或边界框预测。
2. 基于是BEV的方法是稠密方法阵营的一大块
3. BEVFormer 采用了 deformable attention 来计算BEV特征生成和稠密时空特征的融合
4. BEVDet 利用lift-splat operation 实现多视角的变化
5. BEVDepth 加入了深度监督，有效的提高了感知精度
6. BEVStereo 和 SOLOFusion 引入了时间立体技术到3D检测中，进一步提高了深度估计的精度
7. PETR 使用了3D位置编码和全局交叉注意力融合(计算量大，不能算完全的稀疏检测)
8. DETR3D 作为稀疏检测的代表，利用稀疏的参考点进行特征采样和融合
9. Graph DETR3D在DETR3D 基础上，引入了一个图网络来实现更好的空间特征融合，特别是对于多视图重叠区域。

方法

3.1 整体架构

1. 如上图所示，sparse4D 也是编码器-解码器的架构
2. 图像编码器提取图像特征使用共享权重(包括了backbone、neck)
3. 在$t$ 时刻，输入$N$个视角的图片，图片编码器提取的多视角多尺度特征图表示为： T t = { I t , n , s ∣ 1 ≤ s ≤ S ， 1 ≤ n ≤ N } T_{t} = \{ I_{t,n,s}|1≤s≤S，1≤n≤N\} Tt​={It,n,s​∣1≤s≤S，1≤n≤N} （S 表示尺度数）
4. 为了探索时序信息，将图像特征$T$ 作为队列 I = { I t } t = t s t 0 I=\{ I_{t} \}^{t_{0}}_{t=t_{s}} I={It​}t=ts​t0​​,其中:$t_s=t_0-(T-1)$

---

5. 之后，解码器通过迭代优化范式预测结果，其中包括了一系列的优化模块和一个分类头（分类置信度）
6. 每一个优化模块拿图像特征$I$,3D锚框$B\in {\mathbb{R}}^{M\times 11}$ 和相应的实例特征：$F\in {\mathbb{R}}^{M\times C}$ 作为输入
7. 此处，$M$ 是anchor的数量，$C$ 是特征通道数，anchor的格式为：
8. { x , y , z , ln w , ln h , ln l , sin y a w . cos y a w , v x , v y , v z } \{ x,y,z, \text{ln} w, \text{ln} h, \text{ln} l , \text{sin} yaw. \text{cos} yaw, vx, vy, vz \} {x,y,z,lnw,lnh,lnl,sinyaw.cosyaw,vx,vy,vz}
9. 所有的3D锚框 使用了统一的坐标系

---

10. 在每一个优化模块中，首先采用自注意力，让实例之间进行交互，并且会将anchor 信息注入进去
11. 之后，进行可变性 4D 聚合，融合多视角，多尺度，多时间戳下，多关键点的特征
12. 进一步，引入了一个深度reweight模块，缓解基于图像的3D检测的病态解问题。
13. 最后，一个回归头用于预测当前anchor与gt之间的偏差。

3.2 整体架构

1. 实例特征质量在稀疏感知算法中是非常关键的。

2. 为了解决这个问题，如上图所示，引入了一个可变4D聚合模块来获取高质量实例特征，利用稀疏采用和分层聚合。

3. 4D 关键采样点的生成

   1. 对第$m$个实例的anchor，我们分配K个4D关键点：$P_m\in {\mathbb{R}}^{K\times T\times 3}$
   2. 其中有$K_F$个固定点，和$K_L$个可学习的点
   3. 如上图(a),在$t_0$时刻，首先将固定的关键点$P_m^F$, 直接放在锚框的立方体中心和六面中心上。
   4. 之后，不同于固定点，可学习点跟随实例特征发生变化，根据神经网络去寻找最佳特征表征的位置。
   5. 鉴于 特征$F_m$中添加锚框的embeding，可学习的关键点$P_{m,t_0}^L$被生成，根据下面的子网络:$\Phi$
   6. $$\begin{gathered} D_m={\mathbf{R}}_{yaw}\cdot [\mathbf{sigmoid}\left(\Phi (F_m)\right)-0.5]\in {\mathbb{R}}^{K_L\times 3} \\ {P}_{m,t_0}^L=D_m\times [w_m,h_m,l_m]+[x_m,y_m,z_m] \end{gathered}$$
   7. 其中，${\mathbf{R}}_{yaw}$为偏航的旋转矩阵。

   ---

   8. 时间特征是3D检测的关键，可以提高深度估计的精度
   9. 因此，在得到当前帧的3D关键点后，我们将其扩展到4D，为时间融合做准备
   10. 对于过去的时间戳$t$，首先建立一个恒速模型来移动当前坐标系的3D关键点
   11. $P_{m,t}^{\prime }=P_{m,t_0}-d_t\cdot (t_0-t)\cdot [v{x}_m,v{y}_m,v{z}_m]$
   12. 其中$d_t$是两个相邻帧之间的时间间隔
   13. 然后，我们利用自车运动信息将$P_{m,t}^{\prime }$，转换为过去$t$时刻坐标系下
   14. $P_{m,t}={\mathbf{R}}_{t_0\to t}{P}_{m,t}^{\prime }+{\mathbf{T}}_{t_0\to t}$
   15. 其中，${\mathbf{R}}_{t_0\to t}$和${\mathbf{T}}_{t_0\to t}$分别表示自车从当前帧$t_0$到帧$t$的旋转矩阵和平移矩阵
   16. 这样，我们最终可以构造4D关键点为： P ~ m = { P m , t } t = t s t 0 \tilde{P}_{m}=\{P_{m,t}\}_{t=t_{s}}^{t_{0}} P~m​={Pm,t​}t=ts​t0​​

4. Sparse Sampling

   1. 基于上述4D关键点$P$和图像特征映射队列$F$，稀疏具有较强的表示能力，可以有效地进行采样。
   2. 首先，通过变换矩阵$T^{cam}$将4D关键点投影到特征图上。
   3. $P_{t,n}^{\mathrm{img}}={\mathbf{T}}_n^{\mathrm{cam}}{P}_t,1\le n\le N$
   4. 然后，我们通过双线性插值对每个视图和每个时间戳进行多尺度特征采样：
   5. $f_{m,k,t,n,s}=\text{Bilinear}\left(I_{t,n,s},P_{m,k,t,n}^{\text{img}}\right)$
   6. 其中，下标m、k、t、n和s分别表示锚框、关键点、时间戳、相机和特征图多尺度
   7. 到目前为止，我们已经获得了第m个候选检测锚框的多关键点、时间戳、视图和尺度特征向量$f_m\in {\mathbb{R}}^{K\times T\times N\times S\times C}$，其中C是特征通道的数量。

5. Hierarchy Fusion.

   1. 为了生成高质量的实例特征，我们将上述特征向量$f_m$分层融合。
   2. 如图3©所示，对于每个关键点，我们首先用预测的权重, 以不同的视图和尺度聚合特征，然后用线性层进行时间融合。
   3. 最后，对于每个锚框实例，融合多个关键点特征来生成实例特征
   4. 具体来说，给定添加了锚框embeding的实例特征$F_m$，首先通过线性层$\Psi$预测加权系数为:
   5. $W_m=\Psi \left(F_m\right)\in {\mathbb{R}}^{K\times N\times S\times G}$
   6. 其中，G是用通道来划分特征的组数。这样，我们就可以聚合具有不同权重的不同组的通道。类似于group convolution。
   7. 我们将各组的加权后特征向量沿尺度和视角维度相加，然后将各组拼接起来，得到新的特征$f_{m,k,t}^{{}^{\prime }}$。
   8. $\begin{array}{rl}& f_{m,k,t,i}^{{}^{\prime }}=\sum _{n=1}^N\sum _{s=1}^S{W}_{m,k,n,s,i}{f}_{m,k,t,n,s,i}\\ & f_{m,k,t}^{{}^{\prime }}=\left[f_{m,k,t,1}^{{}^{\prime }},f_{m,k,t,2}^{{}^{\prime }},...,f_{m,k,t,G}^{{}^{\prime }}\right]\end{array}$
   9. 上面的下标$i$是组的索引，并且[，]表示连接操作
   10. 接下来，通过拼接操作和线性层Ψtemp，将特征$f_{m,k,t}^{{}^{\prime }}$的时间维度以顺序的方式融合。
   11. $\begin{array}{rl}& f_{m,k,t_s}^{{}^{\prime \prime }}=f_{m,k,t_s}^{{}^{\prime }}\\ & f_{m,k,t}^{{}^{\prime \prime }}={\Psi }_{temp}\left(\left[f_{m,k,t}^{{}^{\prime }},f_{m,k,t-1}^{{}^{\prime \prime }}\right]\right)\\ & f_{m,k}^{{}^{\prime \prime }}=f_{m,k,t_0}^{{}^{\prime \prime }}={\Psi }_{temp}\left(\left[f_{m,k,t_0}^{{}^{\prime }},f_{m,k,t_0-1}^{{}^{\prime \prime }}\right]\right)\end{array}$
   12. 对时间融合后的多关键点特征$f_{m,k}^{{}^{\prime \prime }}$进行求和，完成最终的特征聚合，得到更新后的实例特征为：
   13. $F_m^{\prime }={\sum }_{k=1}^K{f}_{m,k}^{\prime \prime }$

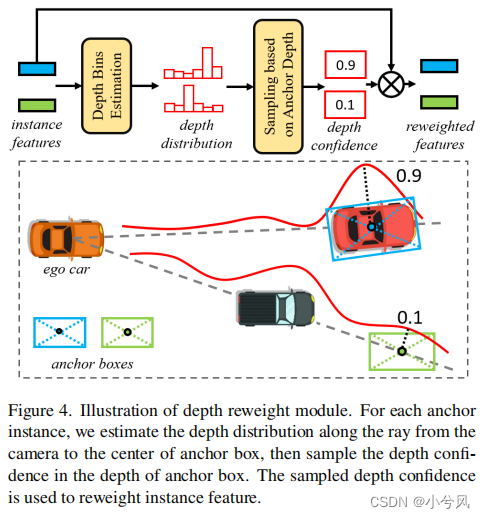
6. Depth Reweight Module
   1. 这个3D到2D的变换(Eq。(5))有一定的模糊性，即不同的3D点可能对应于相同的2D坐标。
   2. 对于不同的三维锚框，可以对相同的特征进行采样（见图4），这增加了神经网络拟合的难度
   3. 为了缓解这一问题，我们加入了一个显式深度估计模块${\Psi }_{depth}$，它由多个具有残差连接的mlp组成。
   4. 对于每个聚合特征$F_m^{{}^{\prime }}$，我们估计一个离散深度分布，并利用3D锚框中心点深度采样相应的置信$C_m$，用于重新加权实例特征。
   5. $$\begin{gathered} C_m=\mathbf{Bilinear}\left({\Psi }_{depth}(F_m^{{}^{\prime }}),\sqrt{x_m^2+y_m^2}\right) \\ {F}_m^{{}^{\prime \prime }}=C_m\cdot F_m^{{}^{\prime }} \end{gathered}$$
   6. 这样，对于那些3D中心点在深度方向上远离地面真相的实例，即使二维图像坐标非常接近地面gt，相应的深度置信度也趋于零
   7. 因此，重新加权后惩罚对应的实例特征$F_m^{{}^{\prime \prime }}$也趋于0。
   8. 结合显式深度估计模块可以帮助视觉感知系统进一步提高感知精度
   9. 此外，深度估计模块也可以作为一个单独的部分进行设计和优化，以促进模型的性能
7. Training
8. 我们用T帧采样视频片段，以端到端训练检测器。
9. 连续帧之间的时间间隔在{dt，2dt)中随机采样（dt≈0.5）
10. 与DETR3D一样 ，使用匈牙利算法将每个地面真相与一个预测值进行匹配。
11. 损失包括三部分：分类损失、边界框回归损失和深度估计损失：
12. $L={\lambda }_1{L}_{cls}+{\lambda }_2{L}_{box}+{\lambda }_3{L}_{depth}$
13. 其中，λ1、λ2和λ3是平衡梯度的权重项。
14. 我们采用focal loss进行分类，采用L1 loss 边界框回归，binary cross entropy loss进行深度估计。
15. .在深度重权模块中，我们直接使用标签的边界框中心的深度作为gt来监督每个实例的深度。
16. 由于只估计每个实例的深度，而不是密集的深度，因此训练过程摆脱了对激光雷达数据的依赖。

实验 Experiment

数据和指标

1. nuScenes数据集
2. 指标：
   1. 平均平均精度（mAP）、平移平均误差（mATE）、尺度平均误差（mASE）、方向平均误差（mAOE）、速度平均误差（mAVE）、属性平均误差（mAAE）和nuScenes检测评分（NDS），
   2. 平均多目标跟踪精度（AMOTA）、平均多目标跟踪精度（AMOTP）和召回率是三个主要的评价指标。

实验细节 Implementation Details

1. 通过对训练集进行K-Means聚类，得到了3D锚框的初始化{x、y、z}参数，
2. 其他参数都用固定值{1、1、1、0、0、0、0、0}初始化。
3. 实例特征使用随机初始化
4. 默认情况下，3D锚框和实例个数M设置为900，级联优化次数为6，neck的特征的尺度个数S为4，固定采样关键点$K_F$为7，可学习关键点$K_L$为6，输入图像大小为640×1600，骨干为ResNet101。
5. sparse4d使用AdamW优化器进行训练
6. 主干网络和其他网络的初始学习率分别为2e-5和2e-4。
7. 衰减策略是余弦退火
8. 初始的网络参数来自于预先训练过的FCOS3D
9. 对于在nuScenes测试集上的实验，网络被训练了48个epoch，而其余的实验只被训练了24个epoch，除非另有说明
10. 为了节省GPU内存，我们在训练阶段将所有历史帧的特征图$f_t^{\prime }$分离。
11. 所有实验均未使用CBGS [50]和测试时间增强。

消融实验 Ablation Studies and Analysis

1. 深度模块和可学习的关键点
   
2. 运动补偿
   
   1. 只加入时序信息，也有mAVE和NDS的提升
   2. 加入自车运动，性能极大提高
   3. 加入目标车辆运动，检测精度没有提高，但是速度误差降低了
3. 优化次数
   1. 
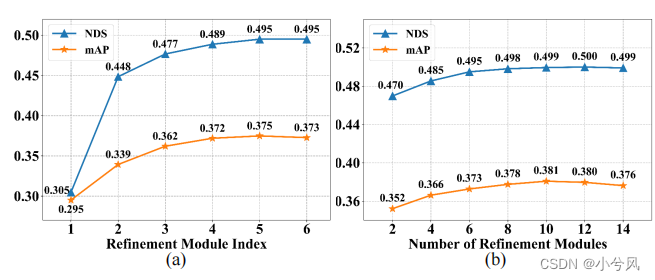
   2. （a）训练的时候优化次数为6，
   3. （b）不停增加优化次数，10次是最好的
4. 历史帧数
   
   1. 随着帧数的增加，还有提升空间.
5. FLOPs and Parameters.
   

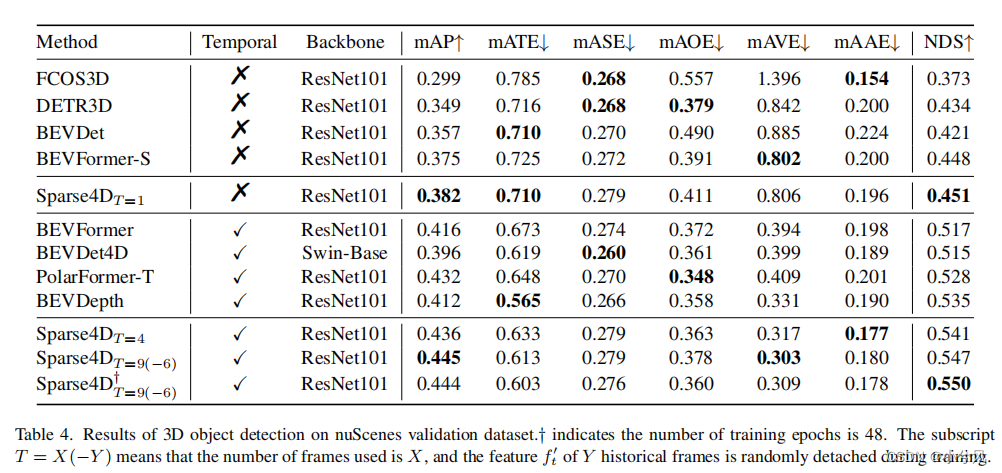
Main Results

1. 
3. 

Extend to 3D Object Tracking

总结

1. 在这项工作中，我们提出了一种新的方法，Sparse4D，该方法通过一个可变形的四D聚合模块，实现了多时间戳和多视图的特征级融合，并使用迭代优化来实现3Dbox的回归
2. Sparse4D可以提供良好的感知性能，并且它在nuScenes排行榜上优于所有现有的稀疏算法和大多数基于bev的算法。
3. 在深度加权模块中，可以添加多视图立体技术，以获得更精确的深度估计。、
4. 在编码器中也可以考虑摄像机参数，以提高三维泛化效果
5. 因此，我们希望Sparse4D可以成为稀疏3D检测的新基线。
6. Sparse4D的框架也可以扩展到其他任务，如高清地图的构建、OCC估计、三维重建等。

阅读时间：2024年6月24日

找博主讨论方式：wx：DL_xifen

讨论QQ群：345458279