14 卡尔曼滤波及代码实现

14.0 基本概念

卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

通俗来说就是，线性数学模型算出预测值+传感器测量值=更准确的测量值。根据数学模型，由第 $k$ 时刻的值递推得到第 $k+1$ 时刻的预测值，结合第 $k+1$ 时刻的观测值，得到第 $k+1$ 时刻更精准的值。

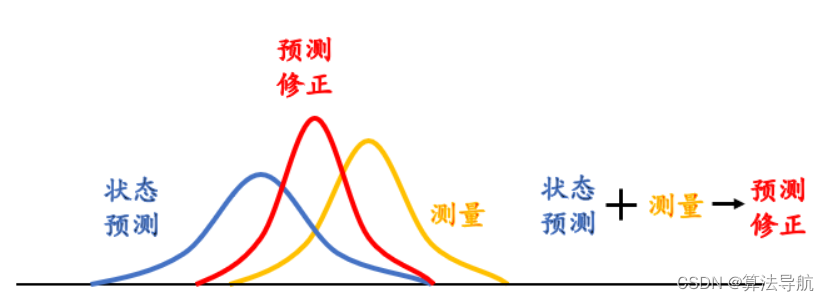
卡尔曼滤波主要用于 线性高斯系统。

14.1 公式推导

（1）线性高斯系统表达

状态方程：

$${\mathbf{x}}_k=\mathbf{A}{\mathbf{x}}_{k-1}+\mathbf{B}{\mathbf{u}}_k+{\mathbf{w}}_k$$

观测方程：

$${\mathbf{z}}_k=\mathbf{H}{\mathbf{x}}_k+{\mathbf{v}}_k$$

其中，${\mathbf{x}}_k$ 为状态量，${\mathbf{z}}_k$ 为观测量，$\mathbf{A}$ 为状态转移矩阵，${\mathbf{B}}_k$ 为控制输入矩阵，$\mathbf{H}$ 为状态观测矩阵。

${\mathbf{w}}_k$ 是过程噪声，服从高斯分布，${\mathbf{w}}_k$ 是观测噪声，也服从高斯分布，即：

$${\mathbf{w}}_k\sim N(0,\mathbf{Q})$$

$${\mathbf{v}}_k\sim N(0,\mathbf{R})$$

其中 $\mathbf{Q}$ 是过程噪声的协方差，$\mathbf{R}$ 是观测噪声的协方差。

卡尔曼滤波包括预测和更新两步。

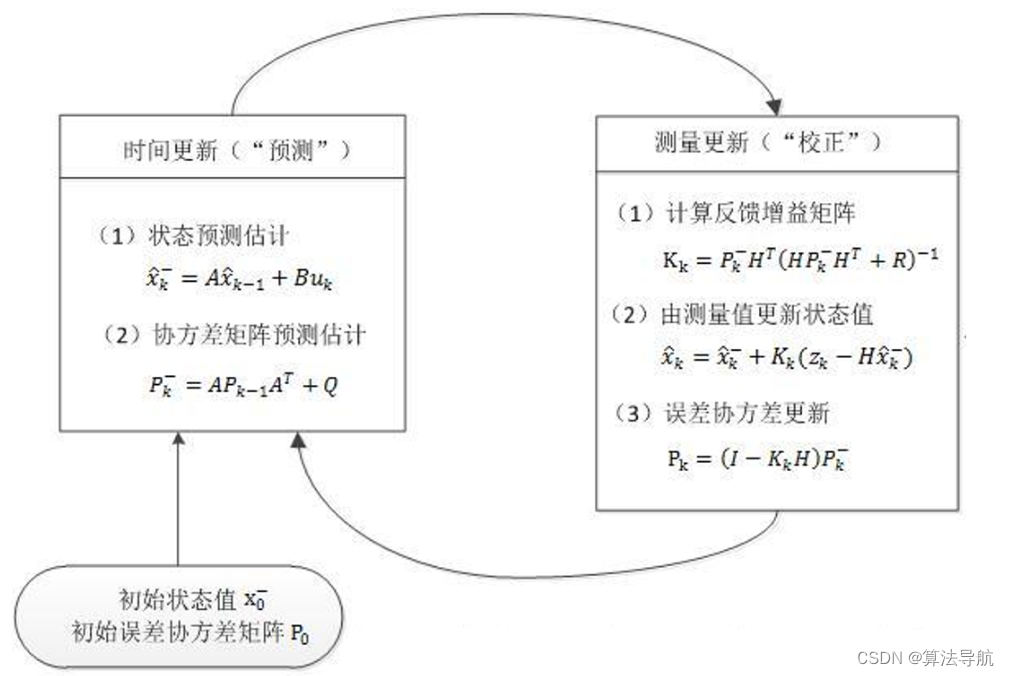
（2）预测（先验）

预测是根据上一时刻的状态量，由状态方程预测出下一时刻的状态量 ${\hat{\mathbf{x}}}_k^{-}$ ，以及状态量误差协方差的先验估计矩阵 ${\mathbf{P}}_k^{-}$。这是没有加观测值的。

$${\hat{\mathbf{x}}}_k^{-}=\mathbf{A}{\hat{\mathbf{x}}}_{k-1}+\mathbf{B}{\mathbf{u}}_k$$

$${\mathbf{P}}_k^{-}={\mathbf{AP}}_{k-1}{\mathbf{A}}^T+\mathbf{Q}$$

其中，$\mathbf{A}{\hat{\mathbf{x}}}_{k-1}$ 是上一时刻的最优估计。

（3）更新（后验）

加入观测，对预测值进行更新校正，得到最优后验估计。

首先计算增益矩阵

$${\mathbf{K}}_k={\mathbf{P}}_k^{-}{\mathbf{H}}^T(\mathbf{H}{\mathbf{P}}_k^{-}{\mathbf{H}}^T+\mathbf{R}{)}^{-1}$$

更新状态量及其协方差矩阵

$${\hat{\mathbf{x}}}_k={\hat{\mathbf{x}}}_k^{-}+{\mathbf{K}}_k({\mathbf{z}}_k-\mathbf{H}{\hat{\mathbf{x}}}_k^{-})$$

$${\mathbf{P}}_k=(\mathbf{I}-{\mathbf{K}}_k\mathbf{H}){\mathbf{P}}_k^{-}$$

14.2 代码实现

以雷达追踪目标为背景，系统的状态方程为

$${\left[\begin{array}{c}x\\ y\\ Vx\\ Vy\\ ax\\ ay\end{array}\right]}_{k+1}=\left[\begin{array}{cccccc}1& 0& {\delta }_t& 0& 0.5{\delta }_t^2& 0\\ 0& 1& 0& {\delta }_t& 0& 0.5{\delta }_t^2\\ 0& 0& 1& 0& {\delta }_t& 0\\ 1& 0& 0& 1& 0& {\delta }_t\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 1\end{array}\right]{\left[\begin{array}{c}x\\ y\\ Vx\\ Vy\\ ax\\ ay\end{array}\right]}_k$$

观测方程

$${\left[\begin{array}{c}x\\ y\end{array}\right]}_{k+1}=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\end{array}\right]{\left[\begin{array}{c}x\\ y\\ Vx\\ Vy\\ ax\\ ay\end{array}\right]}_k$$

/***********************************************************                                          *
* Time: 2023/11/26
* Author: xiaocong
* Function: 卡尔曼滤波
***********************************************************/
#ifndef KALMANFILTER_H
#define KALMANFILTER_H

#include <eigen3/Eigen/Dense>
#include <iostream>

using namespace Eigen;
using namespace std;

class KalmanFilter
{
public:
    KalmanFilter(int stateSize, int measSize, int uSize);               // 构造函数
    void init(VectorXd& x, MatrixXd& P, MatrixXd& R, MatrixXd& Q);      // 初始化
    void predict(MatrixXd& A);
    void predict(MatrixXd& A, MatrixXd& B, VectorXd& u);            // 重载，针对有控制输入的情况
    VectorXd update(MatrixXd& H, VectorXd z_meas);                      // 更新
    ~KalmanFilter();                                                    // 析构函数

private:
    VectorXd x_;         // 状态变量
    VectorXd z_;         // 观测变量
    MatrixXd A_;         // 状态转移矩阵
    MatrixXd B_;         // 控制矩阵
    VectorXd u_;         // 控制变量
    MatrixXd P_;         // 状态值的协方差矩阵
    MatrixXd H_;         // 观测矩阵
    MatrixXd R_;         // 观测噪声协方差矩阵
    MatrixXd Q_;         // 过程噪声协方差矩阵
};

#endif //KALMANFILTER_H

#include "../inlude/KalmanFilter.h"


// 构造函数
KalmanFilter::KalmanFilter(int stateSize, int measSize, int uSize)
{
    if (stateSize == 0 || measSize == 0)
    {
        std::cerr << "Error, State size and measurement size must bigger than 0" << endl;
    }

    x_.resize(stateSize);
    x_.setZero();

    A_.resize(stateSize, stateSize);
    A_.setIdentity();

    u_.resize(uSize);
    u_.setZero();

    B_.resize(stateSize, uSize);
    B_.setZero();

    P_.resize(stateSize, stateSize);
    P_.setIdentity();

    H_.resize(measSize, stateSize);
    H_.setZero();

    Q_.resize(stateSize, stateSize);
    Q_.setIdentity();

    R_.resize(measSize, measSize);
    R_.setIdentity();
}

void KalmanFilter::init(VectorXd& x, MatrixXd& P, MatrixXd& R, MatrixXd& Q)
{
    x_ = x;
    P_ = P;
    R_ = R;
    Q_ = Q;
}

void KalmanFilter::predict(MatrixXd& A)         // 没有控制输入u
{
    A_ = A;
    x_ = A * x_;
    P_ = A_ * P_ * A_.transpose() + Q_;
}

void KalmanFilter::predict(MatrixXd& A, MatrixXd& B, VectorXd& u)       // 有控制输入u
{
    A_ = A;
    B_ = B;
    u_ = u;
    x_ = A * x_ + B * u_;
    P_ = A_ * P_ * A_.transpose() + Q_;
}

VectorXd KalmanFilter::update(MatrixXd& H, VectorXd z_meas)      // 更新
{
    H_ = H;
    MatrixXd temp = H_ * P_ * H_.transpose() + R_;
    MatrixXd K = P_ * H_.transpose() * temp.inverse();
    x_ = x_ + K * (z_meas - H_ * x_);               // 更新 x_k
    MatrixXd I = MatrixXd::Identity(x_.rows(), x_.rows());
    P_ = (I - K * H_) * P_;
    return x_;
}

KalmanFilter::~KalmanFilter()
{

}

#include "../inlude/KalmanFilter.h"
#include <fstream>

#define N 1000
#define T 0.01

double data_x[N], data_y[N];

// 模型函数
double sample(double x0, double v0, double acc, double t)
{
    return x0 + v0 * t + 0.5 * acc * t * t;
}

double getRand()
{
    return 0.5 * rand() / RAND_MAX - 0.25;   //[-0.25, 0.25)
}


int main()
{
    ofstream fout;
    fout.open("../data/data.txt");

    // 生成观测值
    double t;
    for (int i = 0; i < N; i++)
    {
        t = T * i;
        data_x[i] = sample(0, -4.0, 0.1, t) + getRand();
        data_y[i] = sample(0.1, 2.0, 0, t) + getRand();
    }

    int stateSize = 6;
    int measSize = 2;
    int uSize = 0;
    KalmanFilter kf(stateSize, measSize, uSize);

    Eigen::MatrixXd A(stateSize, stateSize);
    A << 1, 0, T, 0, 1 / 2 * T * T, 0,
        0, 1, 0, T, 0, 1 / 2 * T * T,
        0, 0, 1, 0, T, 0,
        0, 0, 0, 1, 0, T,
        0, 0, 0, 0, 1, 0,
        0, 0, 0, 0, 0, 1;

    Eigen::MatrixXd B(0, 0);
    Eigen::MatrixXd H(measSize, stateSize);
    H << 1, 0, 0, 0, 0, 0,
        0, 1, 0, 0, 0, 0;

    Eigen::MatrixXd P(stateSize, stateSize);
    P.setIdentity();

    Eigen::MatrixXd R(measSize, measSize);
    R.setIdentity() * 0.01;

    Eigen::MatrixXd Q(stateSize, stateSize);
    Q.setIdentity() * 0.001;

    Eigen::VectorXd x(stateSize);
    Eigen::VectorXd u(0);
    Eigen::VectorXd z_meas(measSize);
    z_meas.setZero();

    Eigen::VectorXd res(stateSize);         // 存储预测结果

    for (int i = 0; i < N; i++)
    {
        if (i == 0)         // 初始值
        {
            x << data_x[i], data_y[i], 0, 0, 0, 0;
            kf.init(x, P, R, Q);
            continue;
        }

        kf.predict(A);                         // 预测
        z_meas << data_x[i], data_y[i];        // 观测
        res << kf.update(H, z_meas);           // 更新
        fout << data_x[i] << " " << data_y[i] << " " << res[0] << " " << res[1] << " " << res[2] << " " << res[3] << " " << res[4] << " " << res[5] << endl;
    }

    fout.close();
    return 0;

}