二叉树的层序遍历/后序遍历（leetcode104二叉树的最大深度、111二叉树的最小深度）（华为OD悄悄话、数组二叉树）

news2024/9/17 8:34:29

104二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
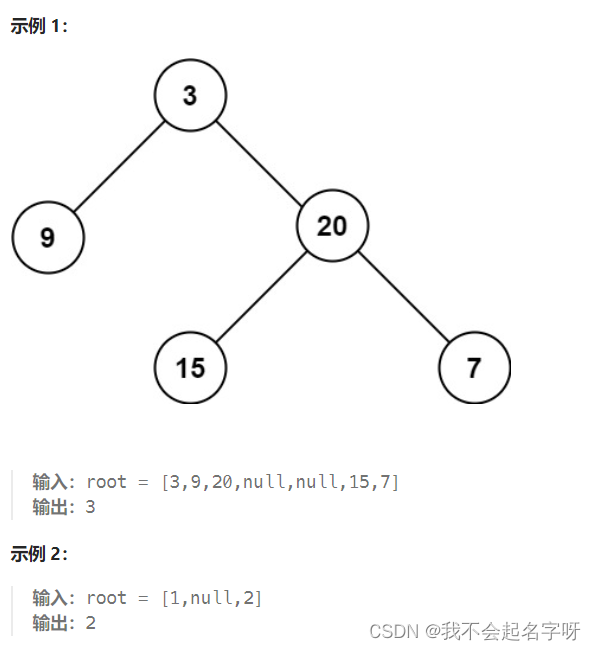
在这里插入图片描述
本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
我先用后序遍历（左右中）来计算树的高度。

1、确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
代码如下：

int getdepth(TreeNode* node)
2、确定终止条件：如果为空节点的话，就返回0，表示高度为0。
代码如下：
```c
if (node == NULL) return 0;
3、确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
代码如下：
`int leftdepth = getdepth(node->left);       // 左
int rightdepth = getdepth(node->right);     // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;``

``int maxDepth(struct TreeNode* root) {
    if(root==NULL) return 0;
    int left=maxDepth(root->left);
    int right=maxDepth(root->right);
    return 1+fmax(left,right);
}

111、二叉树的最小深度

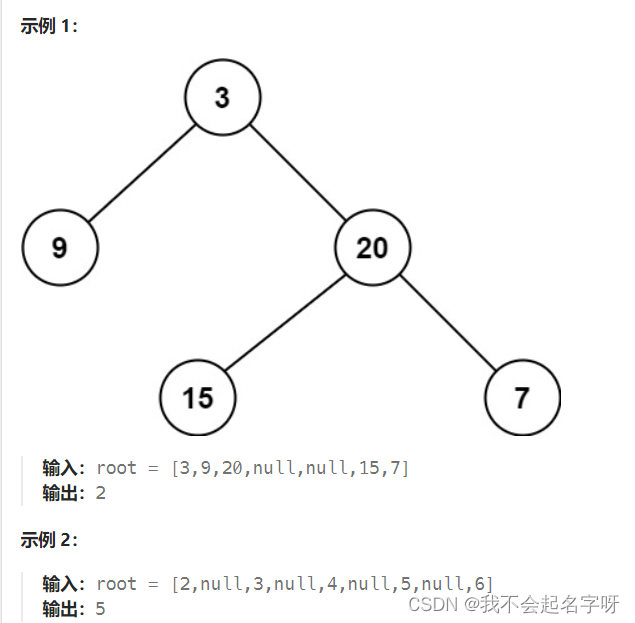
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。
在这里插入图片描述

1 、递归法（后序遍历）

I、确定递归函数的参数和返回值
参数为要传入的二叉树根节点，返回的是int类型的深度。
代码如下：

int getDepth(TreeNode* node)
II、确定终止条件
终止条件也是遇到空节点返回0，表示当前节点的高度为0。
代码如下：

```c
if (node == NULL) return 0;

III、确定单层递归的逻辑

int leftDepth = getDepth(node->left);           // 左
int rightDepth = getDepth(node->right);         // 右
                                                // 中
// 当一个左子树为空，右不为空，这时并不是最低点
if (node->left == NULL && node->right != NULL) { 
    return 1 + rightDepth;
}   
// 当一个右子树为空，左不为空，这时并不是最低点
if (node->left != NULL && node->right == NULL) { 
    return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;

int minDepth(struct TreeNode* root) {
    if(root==NULL) return 0;
    int left= minDepth(root->left);
     int right= minDepth(root->right);
    if(root->left==NULL&&root->right!=NULL)
        return 1+right;
    if(root->left!=NULL&&root->right==NULL)
        return 1+left;
    return 1+fmin(left,right);   
}

2、迭代法（层序遍历）

int minDepth(struct TreeNode* root) {
    struct TreeNode* q[10000];
    if(root==NULL) return 0;
    int depth=0;
    int l=0,r=0;
    q[r++]=root;//将根节点入栈
    while(l<r){
        depth++;
        int len=r-l;
        for(int i=0;i<len;i++){
            root=q[l++];//队头元素为根节点
            if(root->left==NULL&&root->right==NULL)
            return depth;
            if(root->left!=NULL)
            q[r++]=root->left;
            if(root->right!=NULL)
            q[r++]=root->right;
        }
    }
    return depth;
}

华为OD机试C卷（100分）-悄悄话

题目描述

给定一个二叉树，每个节点上站一个人，节点数字表示父节点到该节点传递悄悄话需要花费的时间。
初始时，根节点所在位置的人有一个悄悄话想要传递给其他人，求二叉树所有节点上的人都接收到悄悄话花费的时间。

输入描述

给定二叉树

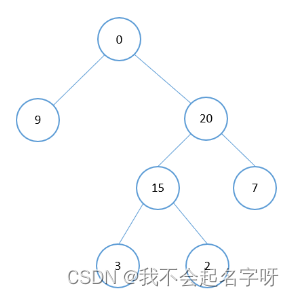
0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2

注：-1表示空节点
在这里插入图片描述

输出描述

返回所有节点都接收到悄悄话花费的时间
38

用例

输入 0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2
输出 38
说明 无

题目解析

题目给的输入信息对照图示来看，应该就是二叉树的层序遍历序列，如下图所示：
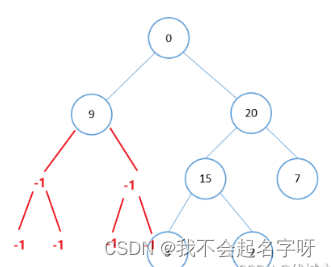
在这里插入图片描述
层序遍历序列中，父子节点存在如下关系：
如果父节点在序列中的索引是k，则其两个子节点在序列中的索引分别为 2k+1, 2k+2
因此，我们就无需建树操作了。
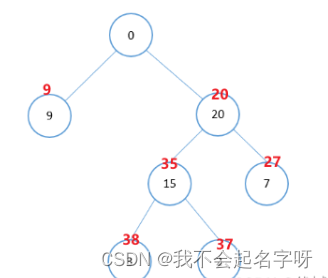
而悄悄话的传递，其实父节点将自身得到消息的时延累加到其各个子节点上，最终叶子节点中最大的时延值就是：二叉树所有节点上的人都接收到悄悄话花费的时间
在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>
int getResult(int *times,int len){
     int ans=0;
     int queue[100];
     int front=0,rear=0;
     queue[rear++]=0;
     while(front<rear){
          int fa=queue[front++];
          int ch1=2*fa+1;
          int ch2=2*fa+2;
          int ch1_exist=ch1<len&&times[ch1]!=-1;
           int ch2_exist=ch2<len&&times[ch2]!=-1;
           if(ch1_exist){
               times[ch1]+=times[fa];
               queue[rear++]=ch1;
           }
           if(ch2_exist){
               times[ch2]+=times[fa];
               queue[rear++]=ch2;
           }
           if(!ch1_exist&&!ch2_exist){
               if(times[fa]>ans)
                    ans=times[fa];
           }
     }
     return ans;
}
int main()
{
     int times[1000];
     int len=0;
     while(scanf("%d",&times[len++])){
          if(getchar()!=' ')break;
     }
    printf("%d\n",getResult(times,len));
    return 0;
}

华为OD机试(C卷,200分)- 数组二叉树

题目描述

二叉树也可以用数组来存储，给定一个数组，树的根节点的值存储在下标1，对于存储在下标N的节点，它的左子节点和右子节点分别存储在下标2N和2N+1，并且我们用值-1代表一个节点为空。
给定一个数组存储的二叉树，试求从根节点到最小的叶子节点的路径，路径由节点的值组成。

输入描述

输入一行为数组的内容，数组的每个元素都是正整数，元素间用空格分隔。
注意第一个元素即为根节点的值，即数组的第N个元素对应下标N，下标0在树的表示中没有使用，所以我们省略了。
输入的树最多为7层。

输出描述

输出从根节点到最小叶子节点的路径上，各个节点的值，由空格分隔，用例保证最小叶子节点只有一个。

用例

输入 3 5 7 -1 -1 2 4
输出 3 7 2
说明 最小叶子节点的路径为3 7 2。
输入 5 9 8 -1 -1 7 -1 -1 -1 -1 -1 6
输出 5 8 7 6
说明 最小叶子节点的路径为5 8 7 6，注意数组仅存储至最后一个非空节点，故不包含节点“7”右子节点的-1。

题目解析

本题有两种思路，一种是从树顶节点向下找，直到找到最小值节点。
这种方式是典型的深度优先搜索。
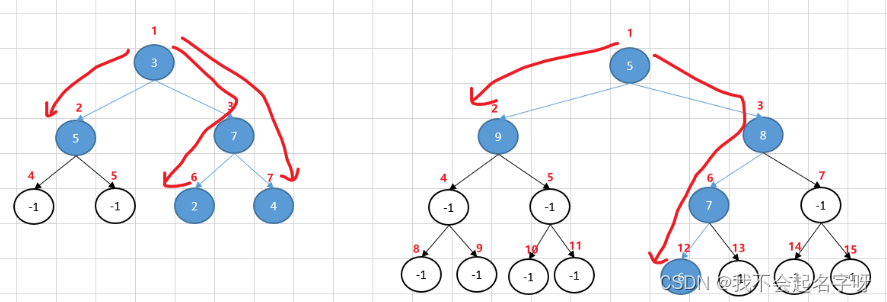
在这里插入图片描述
还有一种思路是先找到最小值节点，然后从最小值节点向上找父节点，由于向上找只有一个父节点，因此只有一种路径。
因此，我们应该选择这种方式。
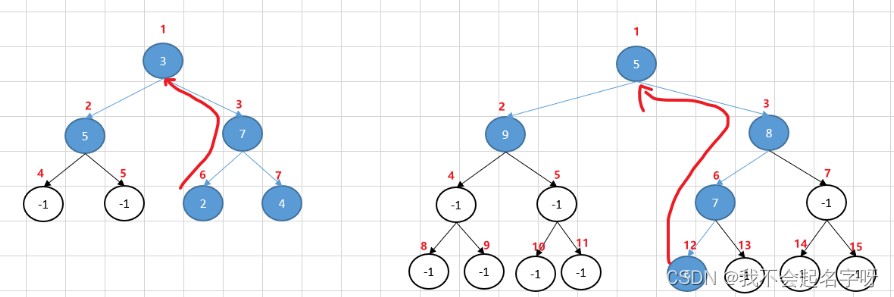
在这里插入图片描述
采用这种方式，首先需要找到最小值节点在数组中的索引位置idx，然后根据题目定义的规则
对于存储在下标N的节点，它的左子节点和右子节点分别存储在下标2N和2N+1
当然上面这个规则是针对根节点索引从1开始的，如果根节点索引从0开始算法，则上面规则应变为
对于存储在下标N的节点，它的左子节点和右子节点分别存储在下标2N+1和2N+2
每找到一个父节点，就将其当成新的子节点，继续向上找父节点，直到子节点本身就是树顶节点为止。
另外，如何找到最小值叶子节点呢？
我们可以反向遍历输入的节点数组，如果遍历的节点符合下面条件，那么他就是一个叶子节点：
自身节点值不为-1
自身没有子节点（即既没有左子节点，也没有右子节点）

#include <stdio.h>
#include <limits.h>
#define MAXSIZE INT_MAX
char* getResult(int arr[], int size) {
    // 最小叶子节点的值
    int minV = MAXSIZE;
    // 最小节点在数组中的索引位置
    int minIdx = -1;
    int n = size - 1;

    for (int i = n; i > 0; i--) {
        if (arr[i] != -1) {
            if (i * 2 + 1 <= n && arr[i * 2 + 1] != -1) {
                continue;
            }
            if (i * 2 + 2 <= n && arr[i * 2 + 2] != -1) {
                continue;
            }

            if (minV > arr[i]) {
                minV = arr[i];
                minIdx = i;
            }
        }
    }

    // path 用于缓存最小叶子节点到根的路径
    char* path = (char*)malloc(100 * sizeof(char));
    int pathIndex = 0;
    char temp[10];
    sprintf(temp, "%d", minV);
    for (int i = 0; temp[i] != '\0'; i++) {
        path[pathIndex++] = temp[i];
        path[pathIndex++] = ' ';
    }

    // 从最小值节点开始向上找父节点，直到树顶
    while (minIdx != 0) {
        int f = (minIdx - 1) / 2;
        sprintf(temp, "%d", arr[f]);
        for (int i = 0; temp[i] != '\0'; i++) {
            path[pathIndex++] = temp[i];
        }
        path[pathIndex++] = ' ';
        minIdx = f;
    }


    path[pathIndex] = '\0';

    return path;
}
void reverseString(char* str) {
    int length = strlen(str)-1;
    for (int i = 0; i < length / 2; i++) {
        char temp = str[i];
        str[i] = str[length - i - 1];
        str[length - i - 1] = temp;
    }
}
int main() {
    // 输入数组
    int arr[1000];
    int n=0;
    while(scanf("%d",&arr[n++])){
     if(getchar()!=' ')break;
    }

    // 调用算法函数
    char* result =getResult(arr, n);
     reverseString(result);

    // 输出结果
    printf("%s\n", result);

    // 释放内存
    free(result);

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1877986.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

自闭症早期风险判别和干预新路径

自闭症早期风险判别和干预新路径

谷禾健康 自闭症谱系障碍 (ASD) 是一组神经发育疾病&#xff0c;其特征是社交互动和沟通的质量障碍、兴趣受限以及重复和刻板行为。 环境因素在自闭症中发挥重要作用&#xff0c;多项研究以及谷禾队列研究文章表明肠道微生物对于自闭症的发生和发展以及存在明显的菌群和代谢物的…
阅读更多...
JVM专题十一：JVM 中的收集器一

JVM专题十一：JVM 中的收集器一

上一篇JVM专题十&#xff1a;JVM中的垃圾回收机制专题中&#xff0c;我们主要介绍了Java的垃圾机制&#xff0c;包括垃圾回收基本概念&#xff0c;重点介绍了垃圾回收机制中自动内存管理与垃圾收集算法。如果说收集算法是内存回收的方法论&#xff0c;那么垃圾收集器就是内存回…
阅读更多...
nginx优势以及应用场景，编译安装和nginx

nginx优势以及应用场景，编译安装和nginx

一. Nginx是什么&#xff1f; 1. Nginx概述 高性能、轻量级Web服务软件系统资源消耗低对HTTP并发连接的处理能力高单台物理服务器可支持30,000&#xff5e;50,000个并发请求Nginx&#xff08;发音同 “engine x”&#xff09;是一个高性能的反向代理和Web服务器软件&#xff0c…
阅读更多...
MySQL之覆盖索引

MySQL之覆盖索引

什么是覆盖索引&#xff1f; 覆盖索引&#xff1a;查询时使用了索引&#xff0c;且需要返回的列&#xff0c;在改索引中已经全部能找到。 示例&#xff1a;有user表如下&#xff1a; CREATE TABLE user (id bigint(20) NOT NULL AUTO_INCREMENT COMMENT 技术主键,name varch…
阅读更多...
Windows 中的 Hosts 文件是什么？如何找到并修改它？

Windows 中的 Hosts 文件是什么？如何找到并修改它？

什么是 Hosts 文件 Hosts 文件是一个纯文本文件&#xff0c;存在于几乎所有的操作系统中&#xff0c;用于将主机名映射到 IP 地址。在域名系统&#xff08;DNS&#xff09;尚未普及之前&#xff0c;Hosts 文件是计算机网络中唯一用于主机名解析的方式。随着网络规模的扩大和 D…
阅读更多...
GPT-4替代大学生参加考试，94%成功作弊未被发现！

GPT-4替代大学生参加考试，94%成功作弊未被发现！

目录 01 「伪装」过程 02 实验结果 03 成绩如何&#xff1f; 调查显示&#xff0c;94%的AI生成内容完全不会被大学教授察觉。 而且在83.4%的情况下&#xff0c;「AI同学」的成绩显著高于人类学生。 看来&#xff0c;AI真的要攻陷人类的考试了。 其实&#xff0c;早在GPT-4发…
阅读更多...
【Mybatis】Mybatis初识-通过源码学习执行流程

【Mybatis】Mybatis初识-通过源码学习执行流程

文章目录 1.Mybatis核心组件1.1 SqlSession1.2 SqlSessionFactory1.3 Mapper1.4 MappedStatement1.5 Executor 2. Mybatis各组件之间关系3. 构建SqlSessionFactory3.1 从XML文件中构建3.2 不使用XML构建SqlSessionFactory 4. 如何从SqlSessionFactory获取SqlSession5.获取Mappe…
阅读更多...
STM32CubeMx的学习记录系列（1） - 软件的下载与点灯

STM32CubeMx的学习记录系列（1） - 软件的下载与点灯

目录 因为最近要学STM32的嵌入式AI开发&#xff0c;但它于是基于STM32CubeMX开发的&#xff0c;就顺便把这个学了。 直接百度STM32CubeMX&#xff0c;到意法的官网去下载。下载过程就看这篇博客 https://blog.csdn.net/as480133937/article/details/98885316 点灯 选择芯片&…
阅读更多...
PG备份与恢复

PG备份与恢复

一、开启WAL归档 1、创建归档目录 我们除了存储数据目录pgdata之外&#xff0c;还要创建backups&#xff0c;scripts&#xff0c;archive_wals文件 mkdir -p /home/mydba/pgdata/arch mkdir -p /home/mydba/pgdata/scripts mkdir -p /home/mydba/backups chown -R mydba.myd…
阅读更多...
PIP一些问题解决办法

PIP一些问题解决办法

研究生期间遇到关于PIP一些问题报错以及解决办法的汇总 pip安装报错&#xff1a;is not a supported wheel on this platform 本节转自 https://blog.csdn.net/happywlg123/article/details/107281936 ​ 出现这个问题&#xff0c;是由于这个whl和系统python版本不匹配导致的。…
阅读更多...
数字人解决方案——数字人类不仅仅是长着一张脸的人工智能

数字人解决方案——数字人类不仅仅是长着一张脸的人工智能

数字人类曾经是简单的聊天机器人&#xff0c;经常误解问题&#xff0c;这让许多人感到沮丧。现在&#xff0c;他们已经发展成为先进的虚拟代理&#xff0c;可以像最好的客户服务代表一样有效地沟通&#xff0c;拥有专家级的知识&#xff0c;并且看起来与真人惊人地相似。 这些…
阅读更多...
基于协同过滤的电影推荐与大数据分析的可视化系统

基于协同过滤的电影推荐与大数据分析的可视化系统

基于协同过滤的电影推荐与大数据分析的可视化系统 在大数据时代&#xff0c;数据分析和可视化是从大量数据中提取有价值信息的关键步骤。本文将介绍如何使用Python进行数据爬取&#xff0c;Hive进行数据分析&#xff0c;ECharts进行数据可视化&#xff0c;以及基于协同过滤算法…
阅读更多...
＜电力行业＞ - 《第7课：发电》

＜电力行业＞ - 《第7课：发电》

1 发电的原理 电力生产的发电环节是利用电能生产设备将各种一次能源或其他形式的能转换为电能。生产电能的主要方式有火力发电、水力发电、核能发电、地热发电、风力发电、太阳能发电、潮汐能发电、生物智能发电和燃料电池发电等。 除太阳能发电的光伏电池技术和燃料电池发电…
阅读更多...
[单机版架设]新天堂2-死亡骑士338|带AI机器人

[单机版架设]新天堂2-死亡骑士338|带AI机器人

前言 今天给大家带来一款单机游戏的架设&#xff1a;新天堂2-死亡骑士338单机服务端—带AI机器人 如今市面上的资源参差不齐&#xff0c;大部分的都不能运行&#xff0c;本人亲自测试&#xff0c;运行视频如下&#xff1a; 新天堂2 搭建教程 此游戏架设不需要虚拟机&#xf…
阅读更多...
利用LLM本身训练SoTA embedding模型

利用LLM本身训练SoTA embedding模型

今天分享一篇Microsoft公司的一篇文章&#xff0c;Title: Improving Text Embeddings with Large Language Models&#xff1a;使用大语言模型改善文本嵌入。 这篇文章探索了直接利用LLM来做embedding模型&#xff0c;其只需要利用合成数据和少于1000次的训练步骤就能获得高质…
阅读更多...
Arthas快速入门

Arthas快速入门

简介 Arthas 是一款线上监控诊断产品&#xff0c;通过全局视角实时查看应用 load、内存、gc、线程的状态信息&#xff0c;并能在不修改应用代码的情况下&#xff0c;对业务问题进行诊断&#xff0c;包括查看方法调用的出入参、异常&#xff0c;监测方法执行耗时&#xff0c;类…
阅读更多...
仓库管理系统12--供应商设置

仓库管理系统12--供应商设置

1、添加供应商窗体 2、布局控件UI <UserControl x:Class"West.StoreMgr.View.SupplierView"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:mc"http://…
阅读更多...
什么是机器学习,机器学习与人工智能的区别是什么（一）?

什么是机器学习,机器学习与人工智能的区别是什么（一）?

人工智能和计算机游戏领域的先驱阿瑟塞缪尔&#xff08;Arthur Samuel&#xff09;创造了 "机器学习"一词。他将机器学习定义为 “一个让计算机无需明确编程即可学习的研究领域” 。通俗地说&#xff0c;机器学习&#xff08;ML&#xff09;可以解释为根据计算机的经…
阅读更多...
前端学习笔记（2406261）：jquery使用checkbox控制页面自动刷新

前端学习笔记（2406261）：jquery使用checkbox控制页面自动刷新

文章目录 需求登录页面主页面 API用户登录login获取数据getdata 代码登录页面主页面 关于后端 需求 这是一个物联网的演示项目&#xff0c;web端能够实时显示后台数据的变化&#xff0c;其流程非常简单&#xff1a; 用户登录登录成功后显示主界面面主界面进入后自动显示数据数…
阅读更多...
Java中的Checked Exception和Unchecked Exception的区别

Java中的Checked Exception和Unchecked Exception的区别

在Java中&#xff0c;异常分为两大类&#xff1a;已检查异常&#xff08;Checked Exception&#xff09;和未检查异常&#xff08;Unchecked Exception&#xff09;。 已检查异常是在编译时必须被捕获或声明的异常。换句话说&#xff0c;如果你的方法可能会抛出某个已检查异常&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023