哈夫曼(Huffman)树,又称最优树,是一类带权路径长度最短的树。
最优二叉树(哈夫曼树)
路径:从树中一个结点到另一个结点之间的分支构成这两个结点之间的路。
路径长度:路径上的分支数目;
树的路径长度:从树根到每一结点的路径长度之和。
在结点数目相同的二叉树中,完全二叉树的路径长度最短。
考虑带权的结点
树的带权路径长度WPL为树中所有叶子结点的带权路径长度之和:
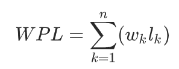
带权路径长度最小的二叉树称为最优二叉树。
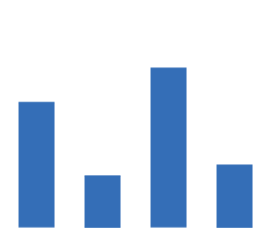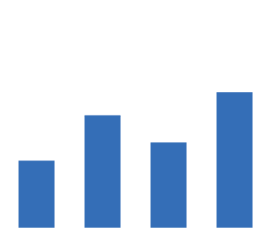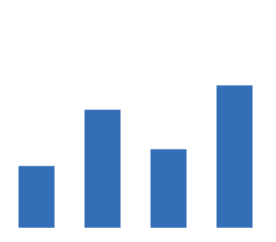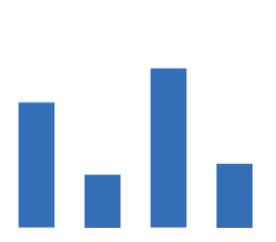
如下图:计算出第三棵树的WPL最小,所以它为哈夫曼树

建立哈夫曼树的核心是贪心算法:选权值小的树
步骤:
1.根据给定的n个权值构成n棵二叉树,并加入集合F,这n个二叉树只有一个根结点,没有左右子树;
2.选择集合F中根结点权值最小的两棵树作为左右子树构造一棵新二叉树,且新二叉树的根结点的权值为其左右子树上根结点的权值之和;
3.在F中删除这两棵树,加入新得到的二叉树;
4.重复2,3直到F只含一棵树,这棵树便是哈夫曼树;
如下图:(小左大右)
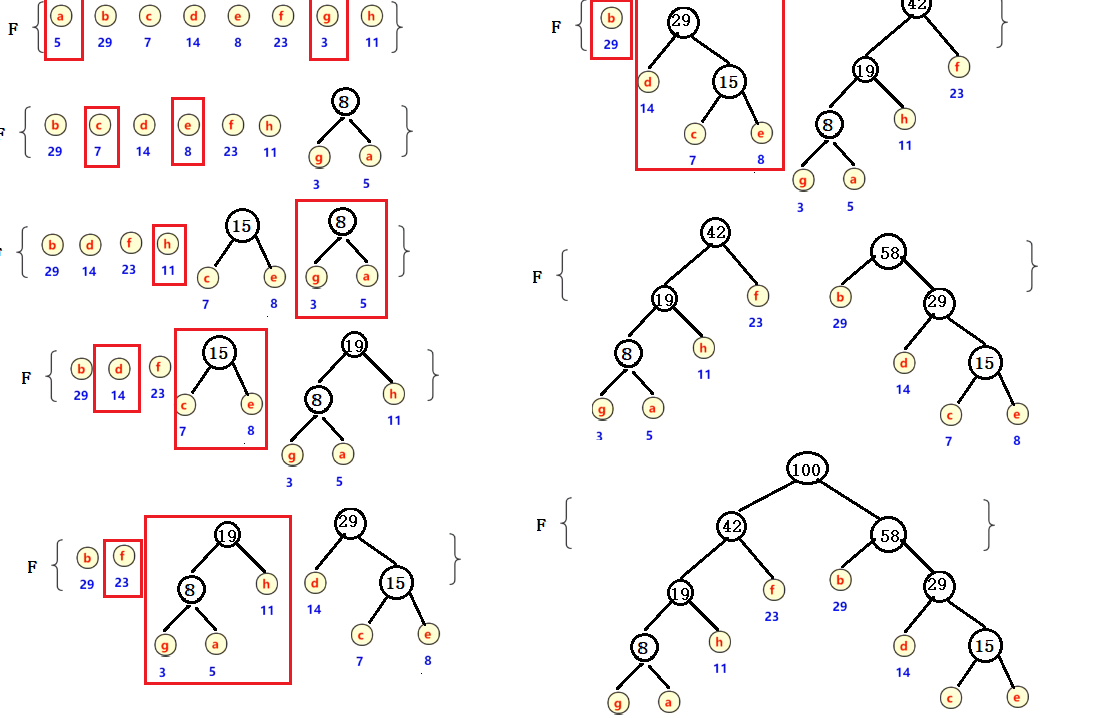
权值越小离根越远,权值越大离根越近
因为要选择根值最小的两个树,所以这个集合中存根的地方用优先级队列,方便出队选择
树的结点结构:
typedef unsigned int WeigthType;
typedef unsigned int NodeType;
typedef struct//结点结构
{
WeigthType weigth;
NodeType parent, leftchild, rightchild;
}HTNode;
typedef HTNode HuffmanTree[m];初始化
void InitHuffManTree(HuffmanTree hft,WeigthType w[])
{
memset(hft, 0, sizeof(HuffmanTree));
for (int i = 0; i < n; i++)
{
hft[i + 1].weigth = w[i];//0下标不用,所以+1
}
//printf("HuffManTree:size%d\n", sizeof(HuffmanTree));//16*16=256(数组类型m(6)个*结构体大小(16))
//printf("hft: size%d\n", sizeof(hft));//4,数组类型在这当指针
//printf("w: size%d\n", sizeof(w));//4,指针
}构建哈夫曼树
因为用优先级队列,我们需要知道结点的原始下标,所以还需创建结构体(包含权值和下标 )传入队列
struct IndexWeigth
{
int index;//下标
WeigthType weight;//权值
operator WeigthType()const { return weight; }
};创建
方法为上面的步骤
void CreatHuffManTree(HuffmanTree hft)
{
priority_queue<IndexWeigth, vector<IndexWeigth>,greater<IndexWeigth>>qu;//greater比较权值
for (int i = 1; i <= n; i++)
{
qu.push(IndexWeigth{ i,hft[i].weigth });//把叶子结点放到优先级队列内
}
int k = n + 1;//分支结点的下标
while (!qu.empty())//取树构建新树
{
if (qu.empty())break;
IndexWeigth left = qu.top(); qu.pop();//取第一小为左边
if (qu.empty())break;
IndexWeigth right = qu.top(); qu.pop();//取第二小为右边
//在分支结点上构建新树
hft[k].weigth = left.weight + right.weight;
hft[k].leftchild = left.index;
hft[k].rightchild = right.index;
hft[left.index].parent = k;
hft[right.index].parent = k;
//将新树放入优先级队列
qu.push(IndexWeigth{ k,hft[k].weigth });
k++;
}
}输出
因为要建树,输出需要知道每个结点的权值、双亲和左右孩子
void PrintHuffManTree(HuffmanTree hft)
{
for (int i = 1; i < m; i++)
{
printf("index%3d weight:%-3d parent:%-3d Lchild:%-3d Rchild:%-3d\n ",
i,hft[i].weigth,hft[i].parent,hft[i].leftchild,hft[i].rightchild);
}
printf("\n");
}主函数
int main()
{
WeigthType w[n] = { 5,29,7,14,8,23,3,11 };
HuffmanTree hft = { 0 };
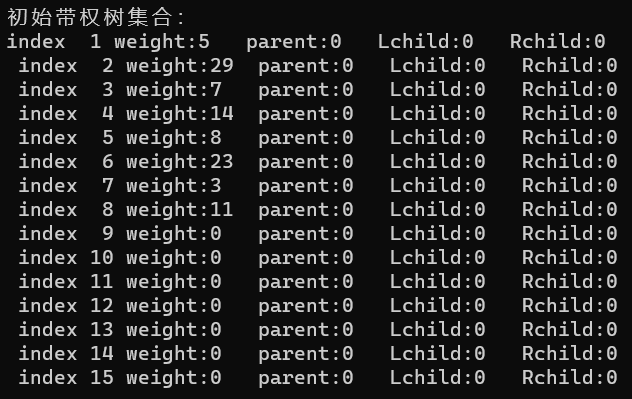
printf("初始带权树集合:\n");
InitHuffManTree(hft, w);//初始化
PrintHuffManTree(hft);//输出
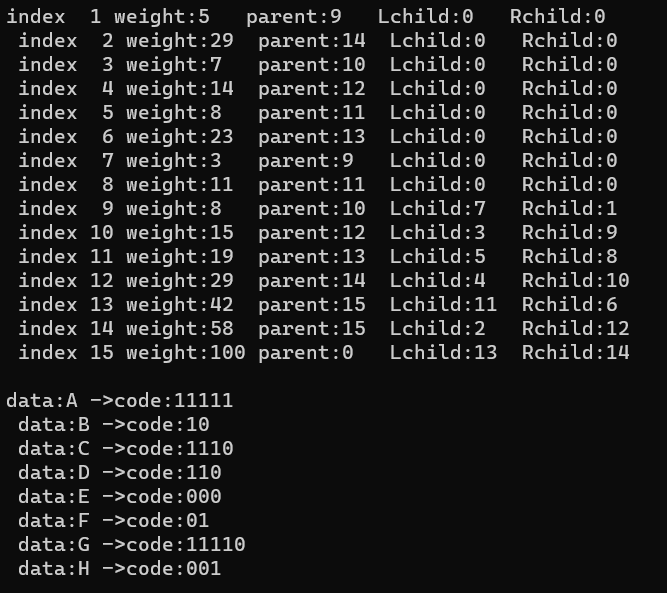
printf("哈夫曼树的结点关系:\n");
CreatHuffManTree(hft);//创建
PrintHuffManTree(hft);
return 0;
}
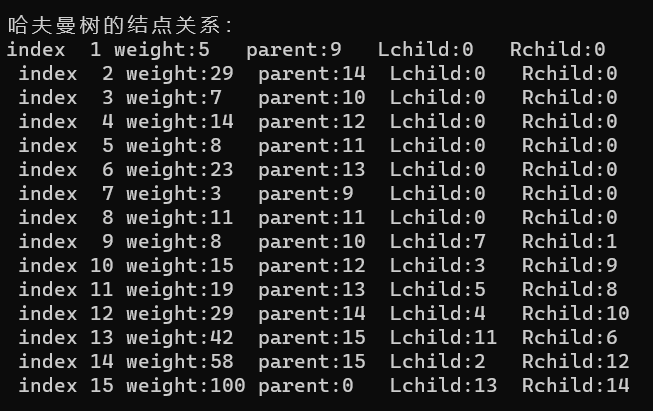
最终结果画出的图:
A:11111 B :10 C :1110 D:110 E :000 F :01 G:11110 H:001
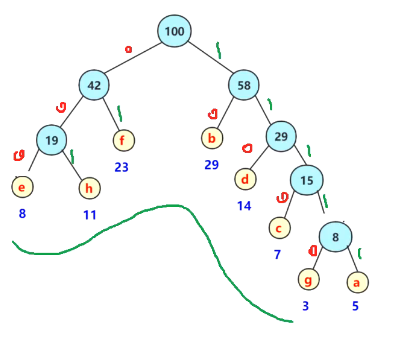
哈夫曼编码
发送电文时希望总长度尽可能的短(压缩),但是必须任意一个字符的编码不能是另一个字符的前缀,否则会有歧义。这种不是其他字符前缀编码的编码叫前缀码。
用哈夫曼树可以创建编码:其左分支表示字符‘0’,右分支表示字符‘1’,可以从根结点到叶子结点的路径上分支字符组成的字符串作为该叶子结点字符的编码。
叶子只有一个双亲所以创建编码时从叶子节点开始,最后把编码倒回来
编码结构体:
字符和其编码
typedef struct
{
char ch;
char code[n + 1];
}HuffCodeNode;
typedef HuffCodeNode HuffCoding[n + 1];//0下标不放数据编码初始化
void InitHuffManCode(HuffCoding hc, const char* ch)
{
memset(hc, 0, sizeof(HuffCoding));
for (int i = 1; i <= n; i++)
{
hc[i].ch = ch[i - 1];
hc[i].code[0] = '\0';
}
}创建编码
void CreatHuffManCode(HuffmanTree hft, HuffCoding hc)
{
char code[n + 1] = { 0 };
for (int i = 1; i <= n; i++)
{//倒过来放
int k = n;
code[k] = '\0';
int c = i;//孩子
int pa = hft[c].parent;//找双亲
while (pa != 0)//没有到根结点
{
code[--k] = hft[pa].leftchild==c ? '0' : '1';//是左孩子0,是右孩子1
c = pa;
pa = hft[c].parent;
}
//正着拷贝
strcpy_s(hc[i].code, n, &code[k]);
}
}输出编码
void PrintfHuffManCode(HuffCoding hc)
{
for (int i = 1; i <= n; i++)
{
printf("data:%c ->code:%s\n ", hc[i].ch, hc[i].code);
}
}主函数
int main()
{
WeigthType w[n] = { 5,29,7,14,8,23,3,11 };
char ch[n + 1] = "ABCDEFGH";
HuffmanTree hft = { 0 };
HuffCoding hc = { 0 };
//初始带权树集合
InitHuffManTree(hft, w);
//编码初始化
InitHuffManCode(hc, ch);
//创建哈夫曼树
CreatHuffManTree(hft);
//创建编码
CreatHuffManCode(hft, hc);
//输出树结点关系
PrintHuffManTree(hft);
//输出编码
PrintfHuffManCode(hc);
return 0;
}