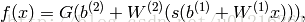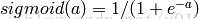目录

.1简介

.2例子

2.1模型

2.2 实例

2.2.1 问题描述

2.2.2 数学过程

.3 代码

3.1 问题描述

3.2 代码

references：

---

.1简介

多层感知机是全连接的

可以把低维的向量映射到高维度

MLP整个模型就是这样子的，上面说的这个三层的MLP用公式总结起来就是，函数G是softmax

输入层没什么好说，你输入什么就是什么，比如输入是一个n维向量，就有n个神经元。（有时候也会加上一个偏置）

隐藏层的神经元怎么得来？首先它与输入层是全连接的，假设输入层用向量X表示，则隐藏层的输出就是

f(W1X+b1)，W1是权重（也叫连接系数），b1是偏置，函数f 可以是常用的sigmoid函数或者tanh函数：

 因此，MLP所有的参数就是各个层之间的连接权重以及偏置，包括W1、b1、W2、b2。对于一个具体的问题，怎么确定这些参数？求解最佳的参数是一个最优化问题，解决最优化问题，最简单的就是梯度下降法了（SGD）：首先随机初始化所有参数，然后迭代地训练，不断地计算梯度和更新参数，直到满足某个条件为止（比如误差足够小、迭代次数足够多时）。这个过程涉及到代价函数、规则化（Regularization）、学习速率（learning rate）、梯度计算等
 

.2例子

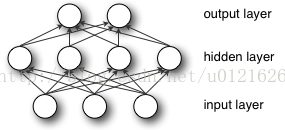
2.1模型

表示了含有一个隐藏层的多层感知器。注意，所有的连接都有权重，但在图中只标记了三个权重（w0,，w1，w2）。

输入层：输入层有三个节点。偏置节点值为 1。其他两个节点从 X1 和 X2 取外部输入（皆为根据输入数据集取的数字值）。和上文讨论的一样，在输入层不进行任何计算，所以输入层节点的输出是 1、X1 和 X2 三个值被传入隐藏层。

隐藏层：隐藏层也有三个节点，偏置节点输出为 1。隐藏层其他两个节点的输出取决于输入层的输出（1，X1，X2）以及连接（边界）所附的权重。

输出层：输出层有两个节点，从隐藏层接收输入，并执行类似高亮出的隐藏层的计算。这些作为计算结果的计算值（Y1 和 Y2）就是多层感知器的输出。

给出一系列特征 X = (x1, x2, ...) 和目标 Y，一个多层感知器可以以分类或者回归为目的，学习到特征和目标之间的关系。

2.2 实例

2.2.1 问题描述

假设我们有这样一个学生分数数据集：

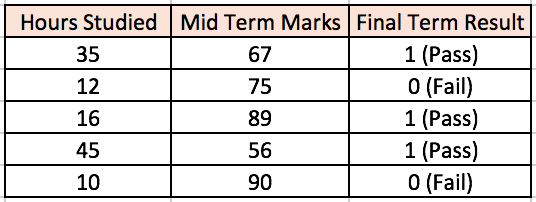
两个输入栏表示了学生学习的时间和期中考试的分数。最终结果栏可以有两种值，1 或者 0，来表示学生是否通过的期末考试。

例如，第一行数据如果学生学习了 35 个小时并在期中获得了 67 分，就会通过期末考试。

现在假设想预测一个学习了 25 个小时并在期中考试中获得 70 分的学生是否能够通过期末考试。

多层感知器（修改自 Sebastian Raschka 漂亮的反向传播算法图解：跳转中...

两个节点分别接收「学习小时数」和「期中考试分数」。感知器也有一个包含两个节点的隐藏层（除了偏置节点以外）。输出层也有两个节点——上面一个节点输出「通过」的概率，下面一个节点输出「不通过」的概率。

在分类任务中，我们通常在感知器的输出层中使用 Softmax 函数作为激活函数，以保证输出的是概率并且相加等于 1。Softmax 函数接收一个随机实值的分数向量，转化成多个介于 0 和 1 之间、并且总和为 1 的多个向量值。

在这个例子中：

概率（Pass）+概率（Fail）=1

2.2.2 数学过程

• 网络的输入=[35, 67]

• 期望的网络输出（目标）=[1, 0]

第一步：前向传播

假设从输入连接到这些节点的权重分别为 w1、w2 和 w3（如图所示）。

涉及到的节点的输出 V 可以按如下方式计算（*f* 是类似 Sigmoid 的激活函数）：

V = f(1*w1 + 35*w2 + 67*w3)

假设输出层两个节点的输出概率分别为 0.4 和 0.6（因为权重随机，输出也会随机）。我们可以看到计算后的概率（0.4 和 0.6）距离期望概率非常远（1 和 0），所以图 5 中的网络被视为有「错误输出」。

第二步：反向传播和权重更新

我们计算输出节点的总误差，并将这些误差用反向传播算法传播回网络，以计算梯度。接下来，我们使用类似梯度下降之类的算法来「调整」网络中的所有权重，目的是减少输出层的误差。

假设附给节点的新权重分别是 w4，w5 和 w6（在反向传播和权重调整之后）。

比，输出节点的误差已经减少到了 [0.2, -0.2]。这意味着我们的网络已经学习了如何正确对第一个训练样本进行分类。

.3 代码

3.1 问题描述

Adam Harley 创造了一个多层感知器的 3D 可视化（http://scs.ryerson.ca/~aharley/vis/fc/）

此网络从一个 28 x 28 的手写数字图像接受 784 个数字像素值作为输入（在输入层有对应的 784 个节点）。网络的第一个隐藏层有 300 个节点，第二个隐藏层有 100 个节点，输出层有 10 个节点（对应 10 个数字）。

虽然这个网络跟我们刚才讨论的相比大了很多（使用了更多的隐藏层和节点），所有前向传播和反向传播步骤的计算（对于每个节点而言）方式都是一样的。

下图显示了输入数字为「5」的时候的网络

输出值比其它节点高的节点，用更亮的颜色表示。在输入层，更亮的节点代表接受的数字像素值更高。注意，在输出层，亮色的节点是如何代表数字 5 的（代表输出概率为 1，其他 9 个节点的输出概率为 0）。这意味着多层感知器对输入数字进行了正确的分类。我非常推荐对这个可视化进行探究，观察不同节点之间的联系。

3.2 代码

网络结构

# 建立一个四层感知机网络
class MLP(torch.nn.Module):   # 继承 torch 的 Module
    def __init__(self):
        super(MLP,self).__init__()    # 
        # 初始化三层神经网络 两个全连接的隐藏层，一个输出层
        self.fc1 = torch.nn.Linear(784,512)  # 第一个隐含层  
        self.fc2 = torch.nn.Linear(512,128)  # 第二个隐含层
        self.fc3 = torch.nn.Linear(128,10)   # 输出层
        
    def forward(self,din):
        # 前向传播， 输入值：din, 返回值 dout
        din = din.view(-1,28*28)       # 将一个多行的Tensor,拼接成一行
        dout = F.relu(self.fc1(din))   # 使用 relu 激活函数
        dout = F.relu(self.fc2(dout))
        dout = F.softmax(self.fc3(dout), dim=1)  # 输出层使用 softmax 激活函数
        # 10个数字实际上是10个类别，输出是概率分布，最后选取概率最大的作为预测值输出
        return dout

加载数据集

# 定义全局变量
n_epochs = 10     # epoch 的数目
batch_size = 20  # 决定每次读取多少图片

# 定义训练集个测试集，如果找不到数据，就下载
train_data = datasets.MNIST(root = './data', train = True, download = True, transform = transforms.ToTensor())
test_data = datasets.MNIST(root = './data', train = True, download = True, transform = transforms.ToTensor())
# 创建加载器
train_loader = torch.utils.data.DataLoader(train_data, batch_size = batch_size, num_workers = 0)
test_loader = torch.utils.data.DataLoader(test_data, batch_size = batch_size, num_workers = 0)

这里参数很多，所以就有很多需要注意的地方了：

root 参数的文件夹即使不存在也没关系，会自动创建

transform 参数，如果不知道要对数据集进行什么变化，这里可自动忽略

batch_size 参数的大小决定了一次训练多少数据，相当于定义了每个 epoch 中反向传播的次数

num_workers 参数默认是 0，即不并行处理数据；我这里设置大于 0 的时候，总是报错，建议设成默认值
网络测试

# 在数据集上测试神经网络
def test():
    correct = 0
    total = 0
    with torch.no_grad():  # 训练集中不需要反向传播
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('Accuracy of the network on the test images: %d %%' % (
        100 * correct / total))
    return 100.0 * correct / total

代码首先设置 torch.no_grad()，定义后面的代码不需要计算梯度，能够节省一些内存空间。然后，对测试集中的每个 batch 进行测试，统计总数和准确数，最后计算准确率并输出。

通常是选择边训练边测试的，这里先就按步骤一步一步来做。

有的测试代码前面要加上 model.eval()，表示这是训练状态。但这里不需要，如果没有 Batch Normalization 和 Dropout 方法，加和不加的效果是一样的。
完整代码

'''
系统环境: Windows10
Python版本: 3.7
PyTorch版本: 1.1.0
cuda: no
'''
import torch
import torch.nn.functional as F   # 激励函数的库
from torchvision import datasets
import torchvision.transforms as transforms
import numpy as np

# 定义全局变量
n_epochs = 10     # epoch 的数目
batch_size = 20  # 决定每次读取多少图片

# 定义训练集个测试集，如果找不到数据，就下载
train_data = datasets.MNIST(root = './data', train = True, download = True, transform = transforms.ToTensor())
test_data = datasets.MNIST(root = './data', train = True, download = True, transform = transforms.ToTensor())
# 创建加载器
train_loader = torch.utils.data.DataLoader(train_data, batch_size = batch_size, num_workers = 0)
test_loader = torch.utils.data.DataLoader(test_data, batch_size = batch_size, num_workers = 0)


# 建立一个四层感知机网络
class MLP(torch.nn.Module):   # 继承 torch 的 Module
    def __init__(self):
        super(MLP,self).__init__()    # 
        # 初始化三层神经网络 两个全连接的隐藏层，一个输出层
        self.fc1 = torch.nn.Linear(784,512)  # 第一个隐含层  
        self.fc2 = torch.nn.Linear(512,128)  # 第二个隐含层
        self.fc3 = torch.nn.Linear(128,10)   # 输出层
        
    def forward(self,din):
        # 前向传播， 输入值：din, 返回值 dout
        din = din.view(-1,28*28)       # 将一个多行的Tensor,拼接成一行
        dout = F.relu(self.fc1(din))   # 使用 relu 激活函数
        dout = F.relu(self.fc2(dout))
        dout = F.softmax(self.fc3(dout), dim=1)  # 输出层使用 softmax 激活函数
        # 10个数字实际上是10个类别，输出是概率分布，最后选取概率最大的作为预测值输出
        return dout

# 训练神经网络
def train():
    #定义损失函数和优化器
    lossfunc = torch.nn.CrossEntropyLoss()
    optimizer = torch.optim.SGD(params = model.parameters(), lr = 0.01)
    # 开始训练
    for epoch in range(n_epochs):
        train_loss = 0.0
        for data,target in train_loader:
            optimizer.zero_grad()   # 清空上一步的残余更新参数值
            output = model(data)    # 得到预测值
            loss = lossfunc(output,target)  # 计算两者的误差
            loss.backward()         # 误差反向传播, 计算参数更新值
            optimizer.step()        # 将参数更新值施加到 net 的 parameters 上
            train_loss += loss.item()*data.size(0)
        train_loss = train_loss / len(train_loader.dataset)
        print('Epoch:  {}  \tTraining Loss: {:.6f}'.format(epoch + 1, train_loss))
        # 每遍历一遍数据集，测试一下准确率
        test()

# 在数据集上测试神经网络
def test():
    correct = 0
    total = 0
    with torch.no_grad():  # 训练集中不需要反向传播
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('Accuracy of the network on the test images: %d %%' % (
        100 * correct / total))
    return 100.0 * correct / total

# 声明感知器网络
model = MLP()

if __name__ == '__main__':
    train()

references：

跳转中...

神经网络快速入门：什么是多层感知器和反向传播？ - 知乎

使用 PyTorch 实现 MLP 并在 MNIST 数据集上验证_rocketeerLi的博客-CSDN博客_mlp pytorch