C++ 图进阶系列之 kruskal 和 Prim 算法_图向最小生成树的华丽转身

news2024/11/15 8:23:00

1. 前言

树和图形状相似，也有差异性。树中添加一条或多条边，可成图。图中减小一条或多条边，可成树。形态的变化由数据之间的逻辑关系决定。

  • 图用来描述数据之间多对多关系。
  • 树用来描述数据之间一对多关系。

思考如下问题？

如果在一座城市城市里铺设一条地铁，要求：

  • 需求通过每一个街区。
  • 线路或造价等最短（少）。

街区之间的逻辑关系可以用无向加权图描述。建设地铁，意味着在图中查找一棵最小生成树，这样才能满足上述要求。

什么是最小生成树？

所谓最小生成村，指从图中找出一棵树，且此树满足如下几个条件：

  • 包含图中的所有顶点。
  • 树中不能有环（每个顶点仅能出现一次）。
  • 树中所有边的权重之和最小。

如果一个算法能同时解决上面的 3 个问题，则称这种算法为图的最小生树算法。

本文讲解kruskal和prim `最小树生成算法。

2. kruskal(克鲁斯卡尔)算法

2.1 算法思想

kruskal是如何解决最小生成树中的 3 个问题？

kruskal算法集结了 2 个核心思想：

  • 贪心思想。

  • 并查集思想。

贪心思想保证权重和最小

kruskal先把图中的边按权重由小到大有序排序，这里的贪心指保证每次选择权重最小的边。如果通过每次选择权重最小的边构成的树显然是权重最小的树。

并查集思想保证顶点的唯一性

树的生成是逐步过程。或者说在生成最小树过程中，有一个边界，把图中的所有顶点分成相对 2 个部分，一个是构成最小生成树的顶点集合，一个是没有加入树的顶点集合，姑且称为其它集合。

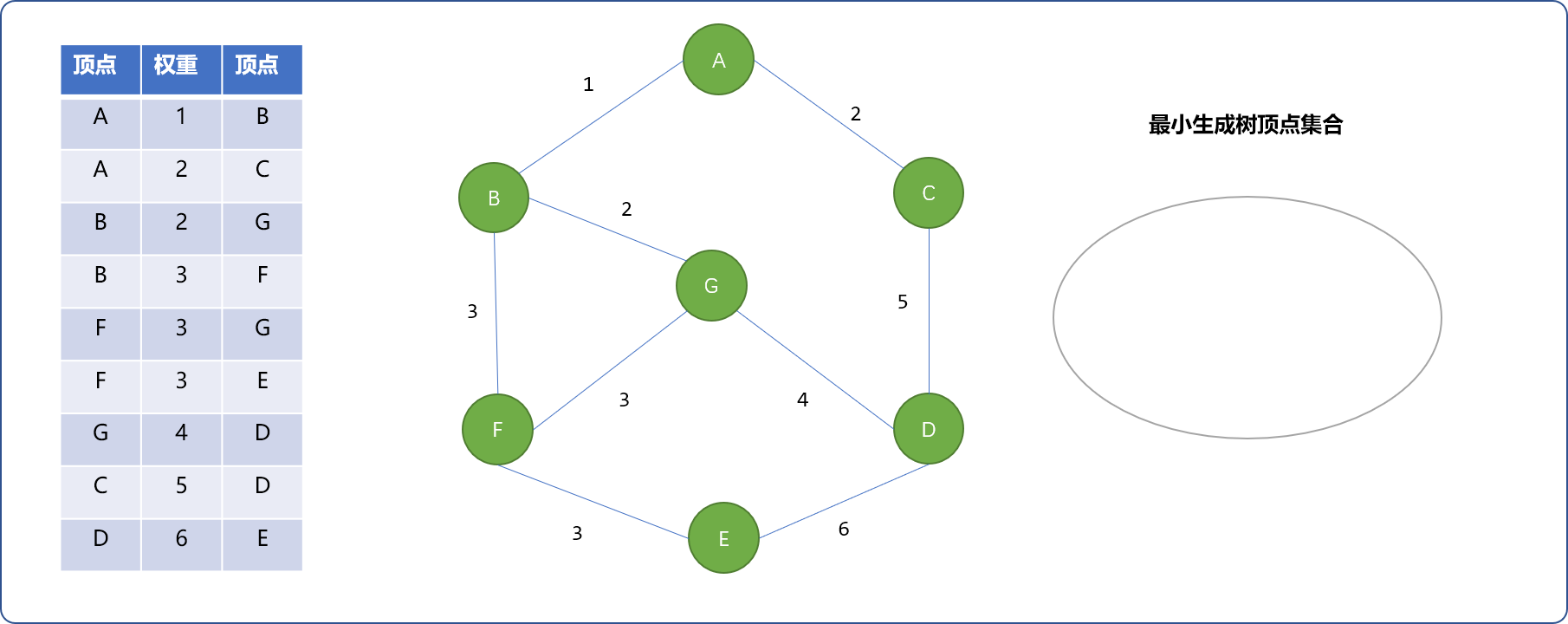
如下图所示，刚开始最小生成树集合是空的。

1.png

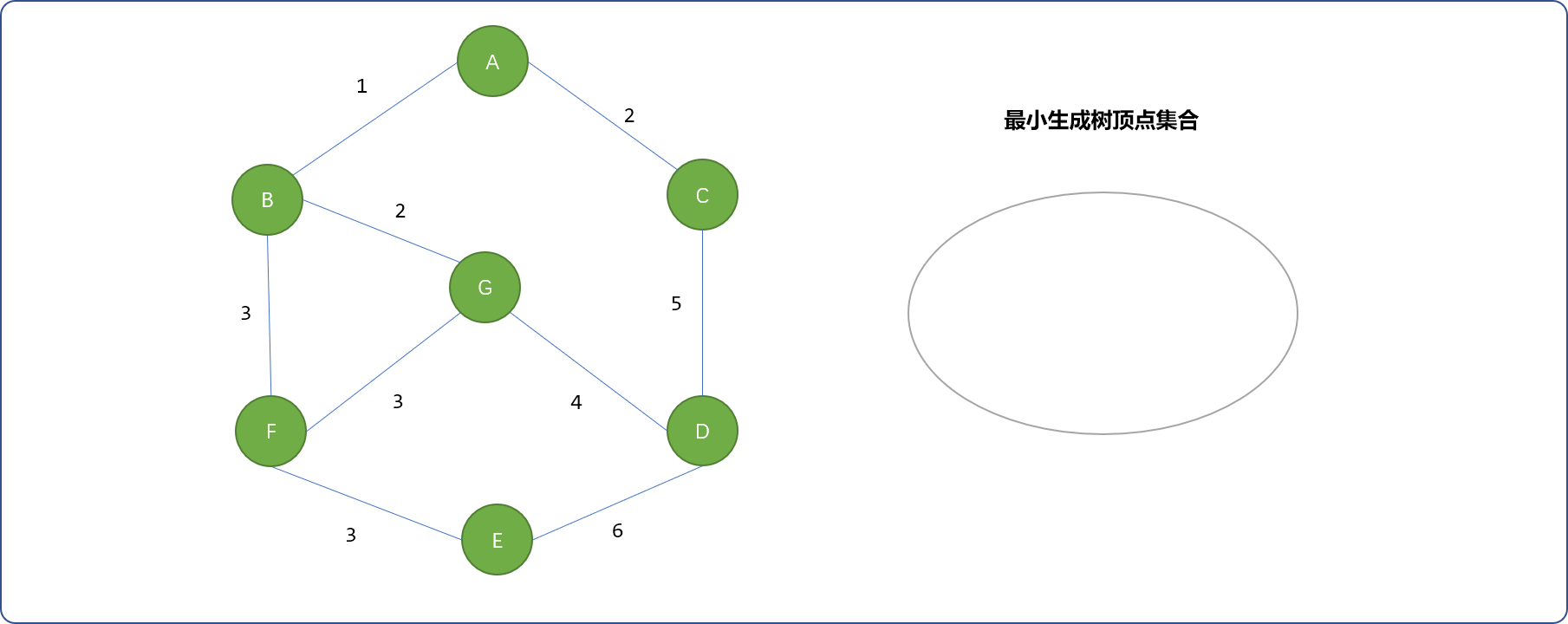
显然，在把图中的顶点加入到最小生成树顶点集合时，是不能把同一个顶点加入 2 次的。并查集可以做到这点。

Tips：那么，如何保证操作过程中顶点选择的唯一性?

算法使用了并查集思想。如果对并查集不是很了解，可以翻阅我的相关博文。

好！现在演示一下kruskal算法的流程。

  • 把图中的边按权重由小到大进行有序排列，且把每一个顶点当成一个独立的集合。如下图所示。

1_1.png

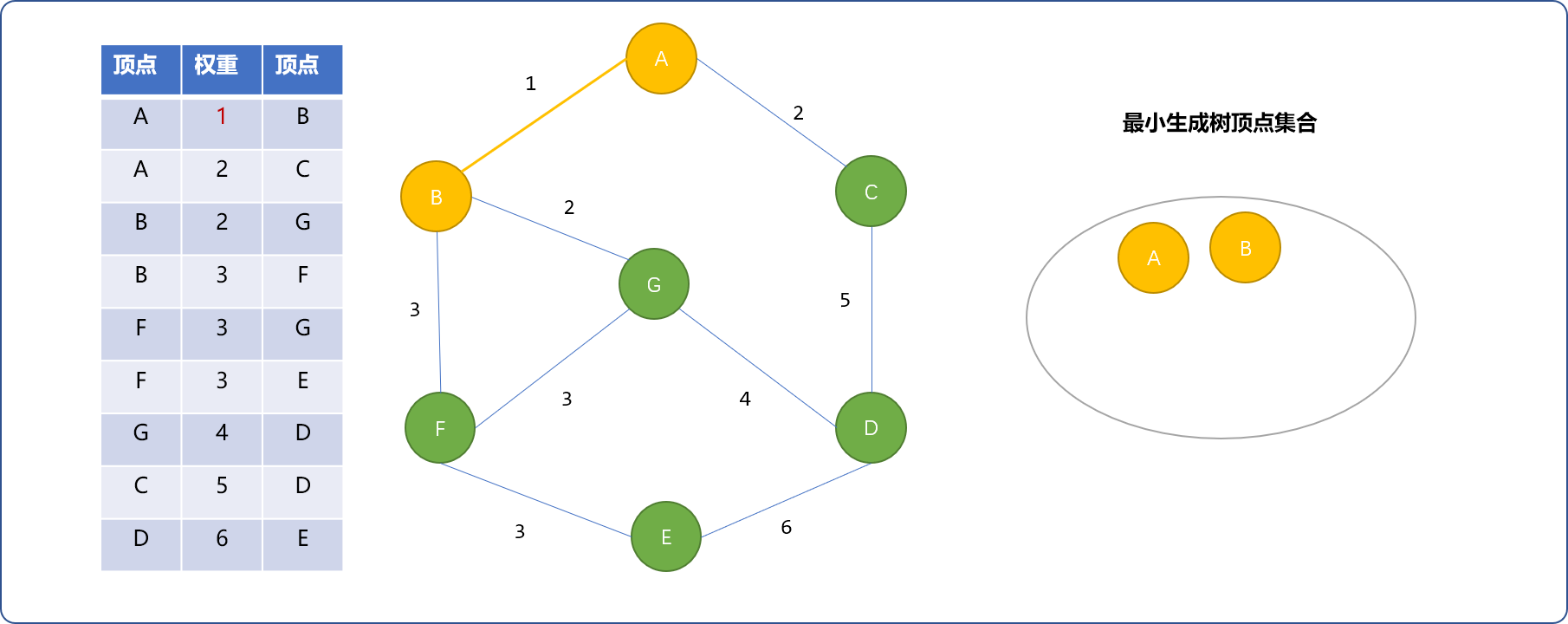
  • 贪心思想：选择权重最小的值为1的边(A,B) 加入到最小生成树集合中。

    并查集思想：刚开始，A和B 两顶点不在同一集合，A和B合并。

2.png

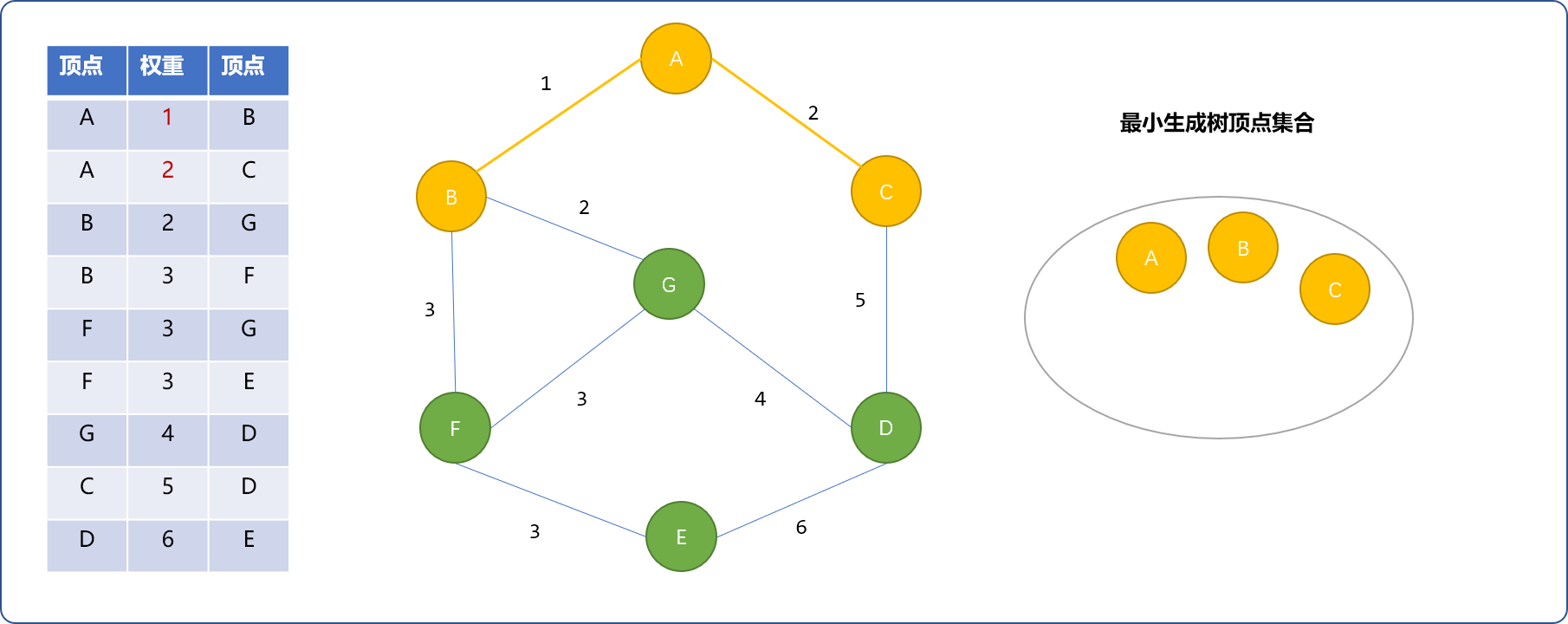
  • 现在权重为2的边有(A,C)和(B,G)，选择(A,C)边。C不在最小生成树顶点集合中，可以加入。

3.png

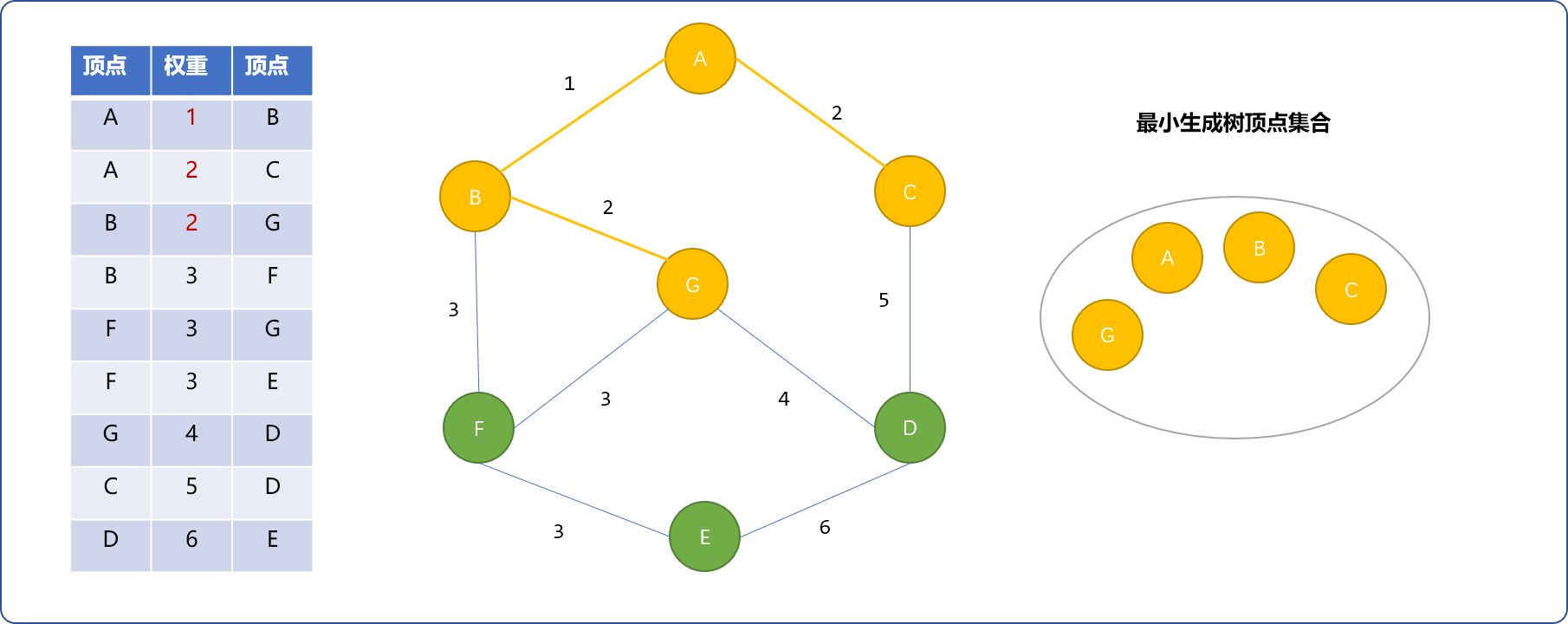
  • 再选择(B,G)。B在最小生成树顶点集合中，G不在，分属2个不同集合，将G加入。

4.png

  • 权重为3的边有 3 条。选择(B,F)。如下图，F加入最小生成树。

5.png

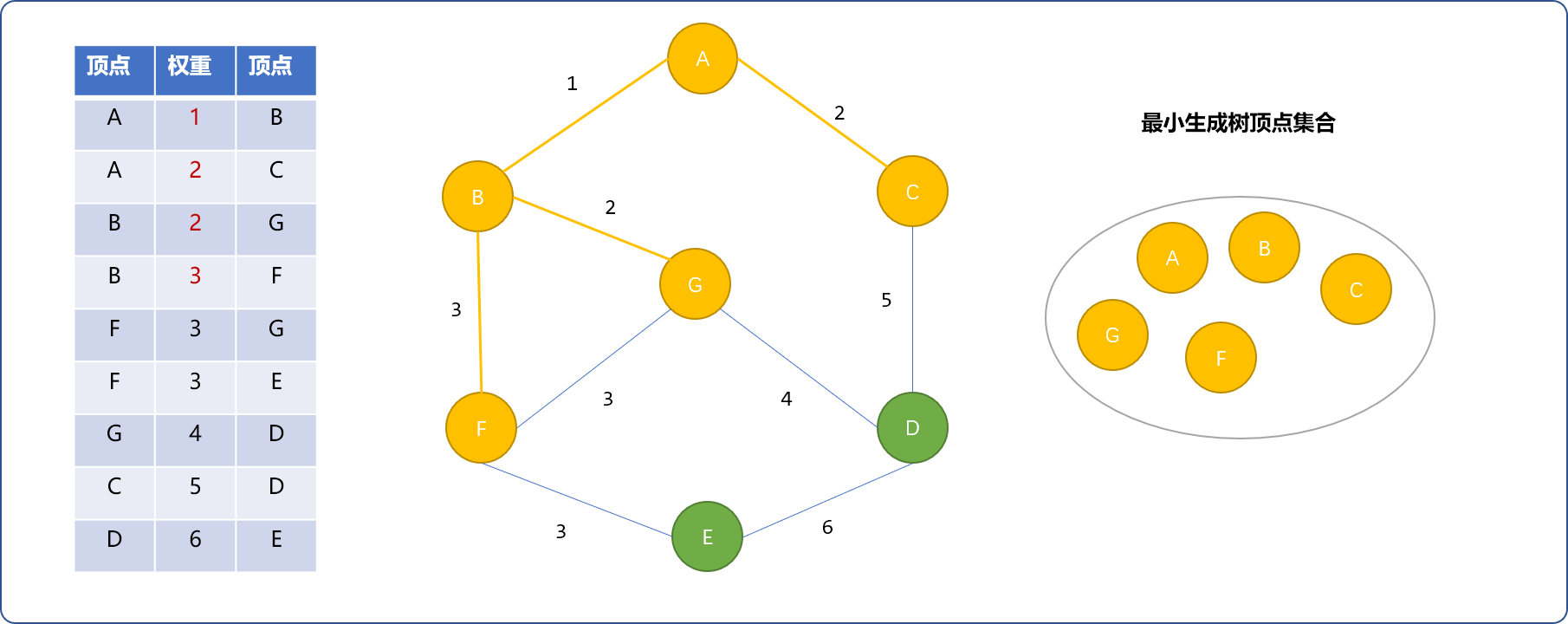
  • 权重为3的(F,G)边不能选择。因为F、G已经在同一个集合中。选择(F,E)，E加入最小生成树集合中。

6.png

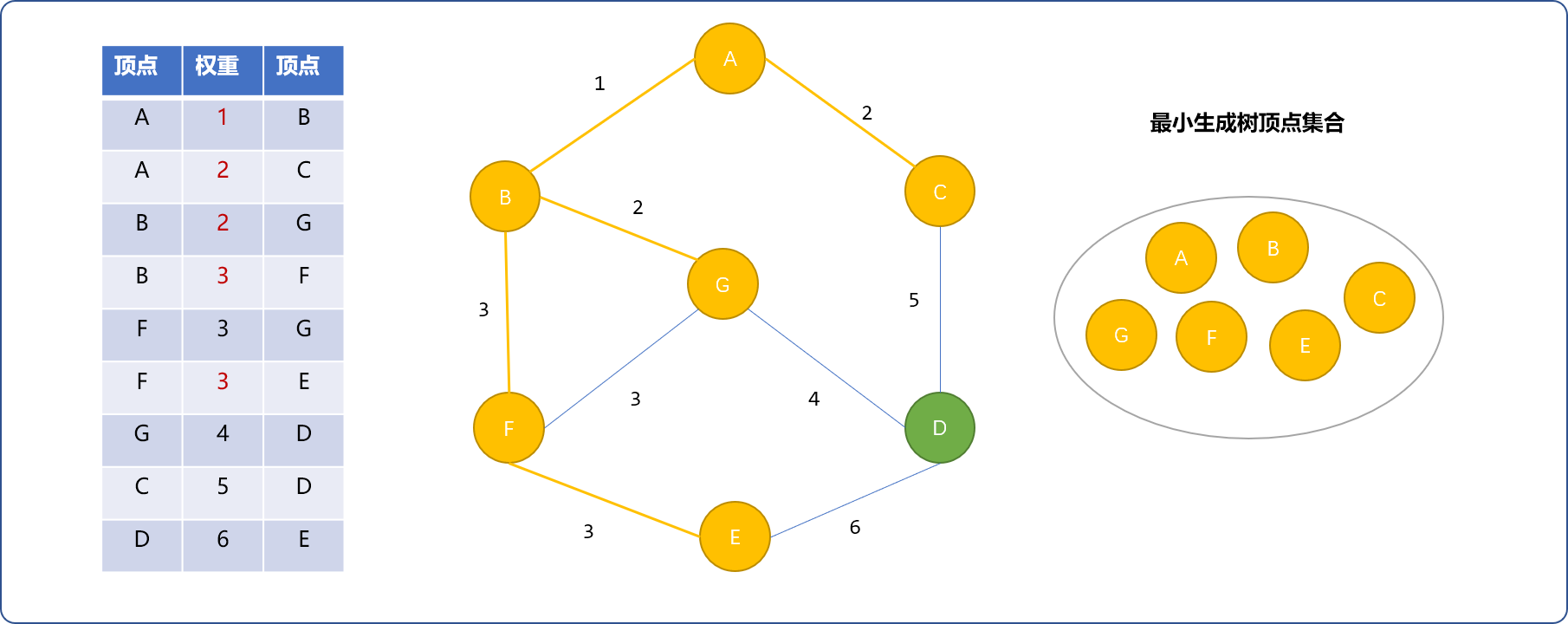
  • 继续选择权重值为4的(G,D)边。D可以加入最小生成树。之后，因为C、D、E已经存在于最小生成树中，(C,D)和(D,E) 边不能加入集合中。至此，最小生成树已经完成，且最小生成树的权重之和为15。

7.png

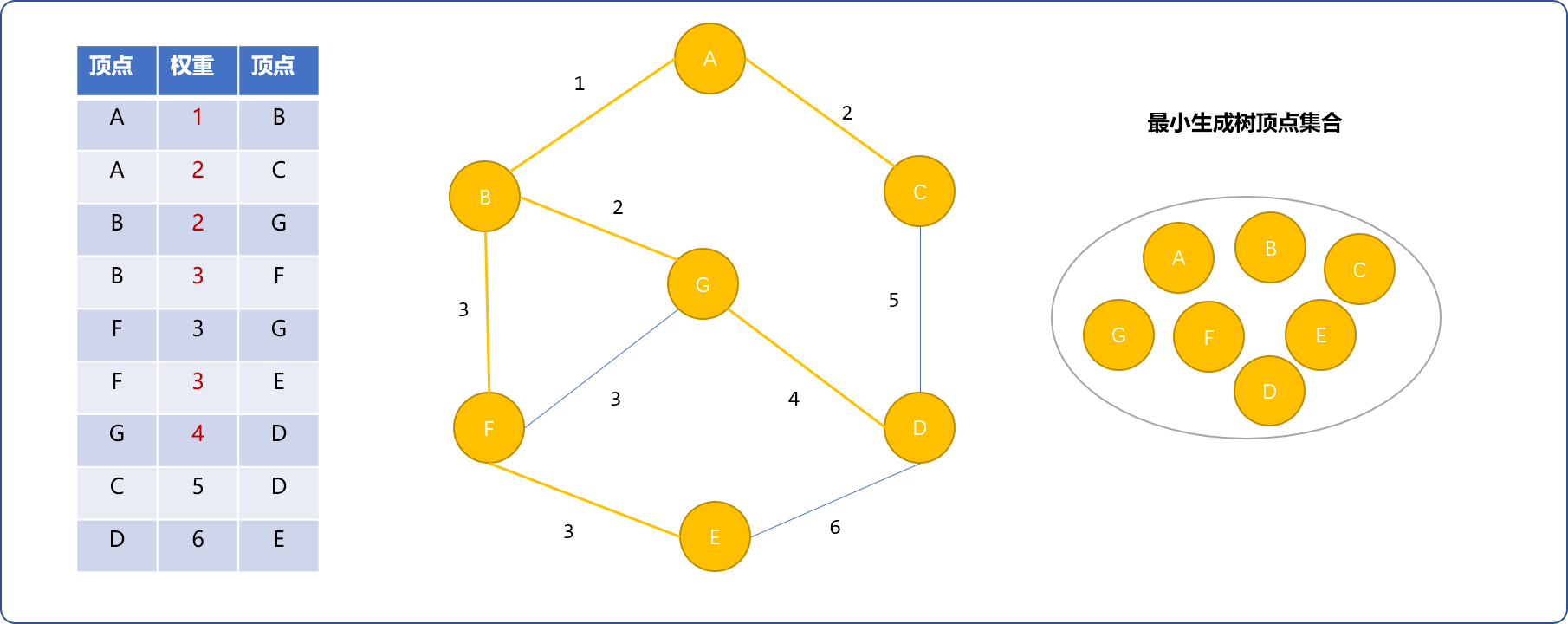
2.1 编码实现

为了让算法具有通用性，下面使用OOP组织代码。程序中有 2 个核心类：

  • 树类。
  • 并查集类。

除此之外，还有辅助类。

2.1.1 树类实现

描述树结构。算法中要用到并查集数据结构，并查集是基于树单位的数据结构。

顶点类： 用来描述树或图的顶点结构。

#include <iostream>
#include <map>
#include <vector>
#include <queue>
using namespace std;
/*
*顶点类型
*/
template<typename T>
struct Vertex {
	//编号
	int code;
	//值
	T value;
	//前驱(父)指针
	Vertex<T>* preVertex;
	//无论是图，还是树，都有多个后驱（子）结点
	map<Vertex<T>*,int> childs;
	Vertex() {
		this->code=-1;
		this->preVertex=NULL;
	}
	Vertex(int code,T value) {
		this->code=code;
		this->preVertex=NULL;
		this->value=value;
	}
	/*
	* 添加子结点及与其权重
	*/
	Vertex<T>* addChild(Vertex<T>* vertex,int weight=1) {
		this->childs[vertex]=weight;
	}
	/*
	*重载 == 运算符
	*/
	bool operator==(Vertex<T>* vertex) {
		return this->code==vertex->code && this->value==vertex->value;
	}
	/*
	*重载 < 运算符
	*/
	bool operator<(Vertex<T>* vertex) {
		return this->code<vertex->code;
	}
	/*
	*输出结点信息
	*/
	int desc() {
		cout<<"结点名称："<<this->value<<endl;
		typename::std::map<Vertex<T>*,int>::iterator begin=this->childs.begin();
		typename::std::map<Vertex<T>*,int>::iterator end=this->childs.end();
		if(begin==end)cout<<"\t叶结点"<<endl;
		int weight=0;
		//查找子结点
		while(begin!=end) {
			Vertex<T>* child=begin->first;
			cout<<"\t子结点名称："<<child->value<<"权重："<<begin->second<<endl;
			weight+=begin->second;
			begin++;
		}
		return weight;
	}
};

树类： 提供维护树顶点的函数。

template<typename T>
class Tree {
	private:
		//根结点
		Vertex<T>* root=NULL;
		//存储所有结点
		vector<Vertex<T>*> vertexs;
		//大小
		int size=0;
		//树的权重之和
		int totalWeight=0;
	public:
		Tree() {
		}
		Tree(Vertex<T>* root) {
			this->setRoot(root);
			this->vertexs.push_back(this->root);
		}
		Tree(T val) {
			//编号从 1 开始
			this->size++;
			this->root=new Vertex<T>(this->size,val);
			this->vertexs.push_back(this->root);
		}
        //重置根结点
		void setRoot(Vertex<T>* root) {
			this->root=root;
		}
		/*
		*返回根结点
		*/
		Vertex<T>*  getRoot() {
			return this->root;
		}
		/*
		*返回树中所有结点
		*/
		vector<Vertex<T>*> getVertexs() {
			return this->vertexs;
		}
		/*
		*根据值查找结点是否存在
		*/
		Vertex<T>* findVertex(T value) {
			for(int i=0; i<this->size; i++) {
				if(this->vertexs[i]->value==value )return this->vertexs[i];
			}
			return NULL;
		}
		/*
		*查找结点是否存在
		*/
		Vertex<T>* findVertex(Vertex<T>* ver) {
			for(int i=0; i<this->vertexs.size(); i++) {
				if(this->vertexs[i]==ver )return this->vertexs[i];
			}
			return NULL;
		}

		/*
		* 根据节点值返回此树的根节点
		* 算法中，需要根据元素得知其所在的树
		* 根结点是每一棵树的唯一标志符
		*/
		Vertex<T>* getRoot(T value) {
			if(this->findVertex(value)!=NULL)return this->root;
		}
		/*
		*添加结点
		*/
		bool addVertex(Vertex<T>* ver) {
			if( this->findVertex(ver)==NULL) {
				//没有，添加
				this->vertexs.push_back(ver);
				//成功
				return true;
			}
			return false;
		}
		/*
		*合并另一颗树中的结点
		*/
		void unionTree(Tree<T>* tree) {
			//另一棵树的所有结点
			vector<Vertex<T>*> vers=tree->getVertexs();
			for(int i=0; i<vers.size(); i++)
				//合并
				this->vertexs.push_back(vers[i]);
			//修改数量
			this->size+=vers.size();
		}
		/*
		*显示树中所有结点
		*/
		void showAll() {
			cout<<"------------树 "<<this->root->value<<"------------"<<endl;
			for(int i=0; i<this->vertexs.size(); i++) {
				this->totalWeight+=this->vertexs[i]->desc();
			}
			cout<<"------------最小生成树的权重 "<<this->totalWeight<<"------------"<<endl;
		}
};

2.2.2 实现kruskal算法

本质是使用并查集合并指定边两端的顶点。

//描述图中顶点与顶点之间的关系
template<typename T>
struct Edge {
	T from;
	T to;
	int weight;
};
/*
* Kruskal 算法
*/
template<typename T>
class Kruskal {
	private:
		//集合群（森林）
		map<Vertex<T>*,Tree<T>*> trees;
		//森林中树的数量
		int size;
	public:
        /*
        *构造集合（森林）群
        */
		Kruskal(T datas[],int size) {
			this->size=size;
			this->initSets(datas);
		}
		/*
		*初始化森林
		*/
		void initSets(T datas[]) {
			for(int i=0; i<this->size; i++ ) {
				//创建只有根结点的树
				Tree<T>* tree=new Tree<T>(datas[i]);
				//存入集合群
				this->trees[tree->getRoot()]=tree;
			}
		}
		/*
		* 通过节点值查找其所在的树(集合)
		* 返回树的根结点（唯一标志符）
		*/
		Vertex<T>* find(T value) {
			typename::std::map<Vertex<T>*,Tree<T>*>::iterator begin=trees.begin();
			typename::std::map<Vertex<T>*,Tree<T>*>::iterator end=trees.end();
			while(begin!=end) {
				Tree<T> *tree=begin->second;
				Vertex<T>* root=tree->getRoot(value);
				if(root!=NULL)return root;
				begin++;
			}
			return NULL;
		}
		/*
		*合并树
		*/
		bool unionSet(T from,T to,int weight=1) {
			Vertex<T>* root =this->find(from);
			Vertex<T>* root_ =this->find(to);
            //同一棵树
			if(root==root_)return false;
			Vertex<T>* ver=this->trees[root]->findVertex(from);
			Vertex<T>* ver_=this->trees[root_]->findVertex(to);
             //合并两个顶点
			ver->addChild(ver_,weight);
			//合并树
			this->trees[root]->unionTree(this->trees[root_] );
			//删除
			this->trees.erase(root_);
			this->size--;
		}
		/*
		*查找最小生成树
		*/
		void kruskal_(Edge<T> relation[]) {
			for(int i=0; i<sizeof(relation)/sizeof(T); i++) {
				this->unionSet(relation[i].from,relation[i].to,relation[i].weight);
			}
		}
		/*
		*输出最小生成树
		*/
		void showAllTree() {
			typename::std::map<Vertex<T>*,Tree<T>*>::iterator begin=trees.begin();
			typename::std::map<Vertex<T>*,Tree<T>*>::iterator end=trees.end();
			while(begin!=end) {
				Vertex<T>* root=begin->first;
				Tree<T> *tree=begin->second;
				tree->showAll();
				begin++;
			}
		}
};

测试： 简化了图的描述，直接提供已经排序的信息，侧重测试算法设计是否准确。

int main(int argc, char** argv) {
	char datas[7]= {'A','B','C','D','E','F','G'};
    //硬代码，对图中的边按权重由小到大排序
	Edge<char> relations[9]= { {'A','B',1}, {'A','C',2},{'B','G',2},{'B','F',3},{'F','G',3},{'F','E',3},{'G','D',4},{'C','D',5},{'D','E',6} };
    //初始算法
	Kruskal<char> kruskal(datas,7);
	kruskal.kruskal_( relations);
	kruskal.showAllTree();
	return 0;
}

输出结果：和前文演示结果一致。

8.png

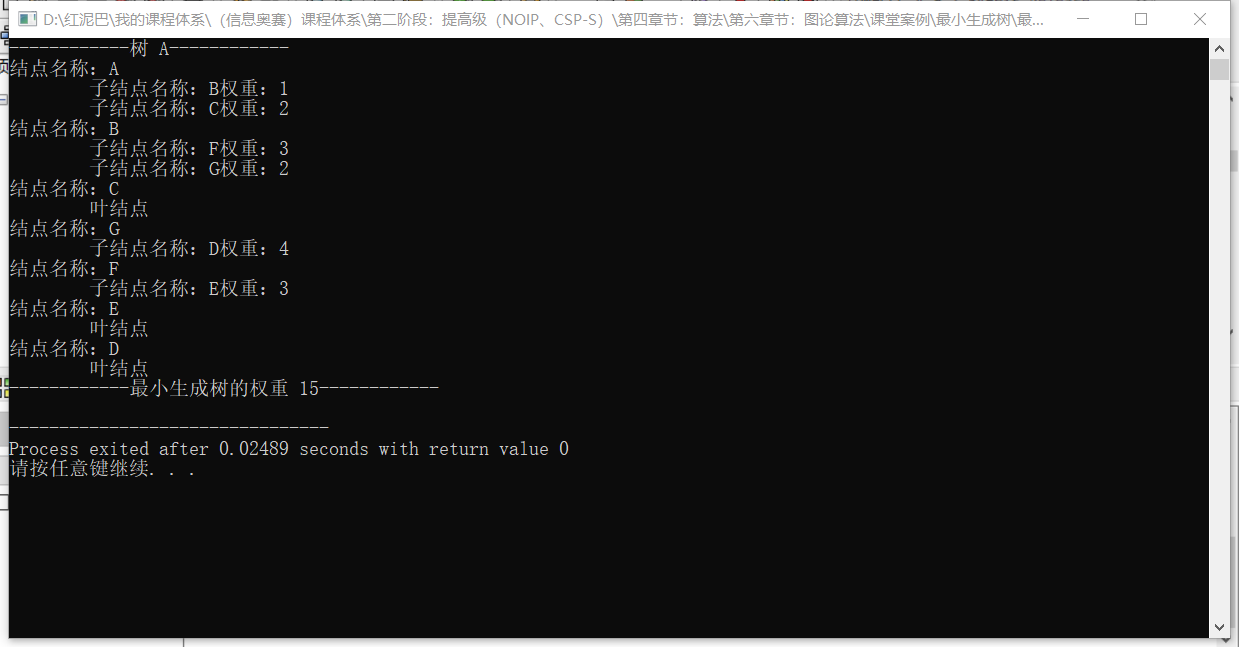
3. Prim(普里姆) 算法

Prim算法核心也是贪心思想，算法流程类似于最短路径算法Dijkstra算法。

相比较于kruskal，前者基于静态信息（提前对边按权重排序），后者基于动态信息（由优先队列随时调整）。

3.1 算法流程

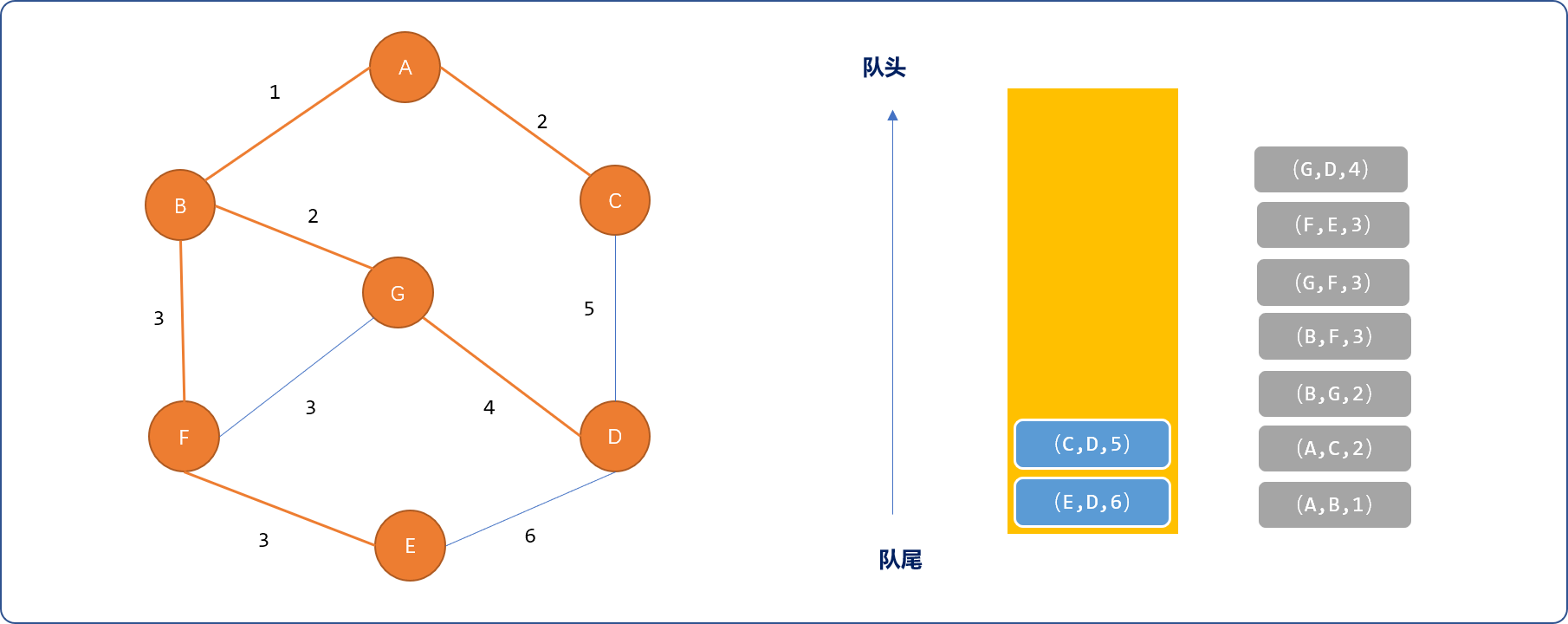
如查询如下图结构的最小生成树。

9.png

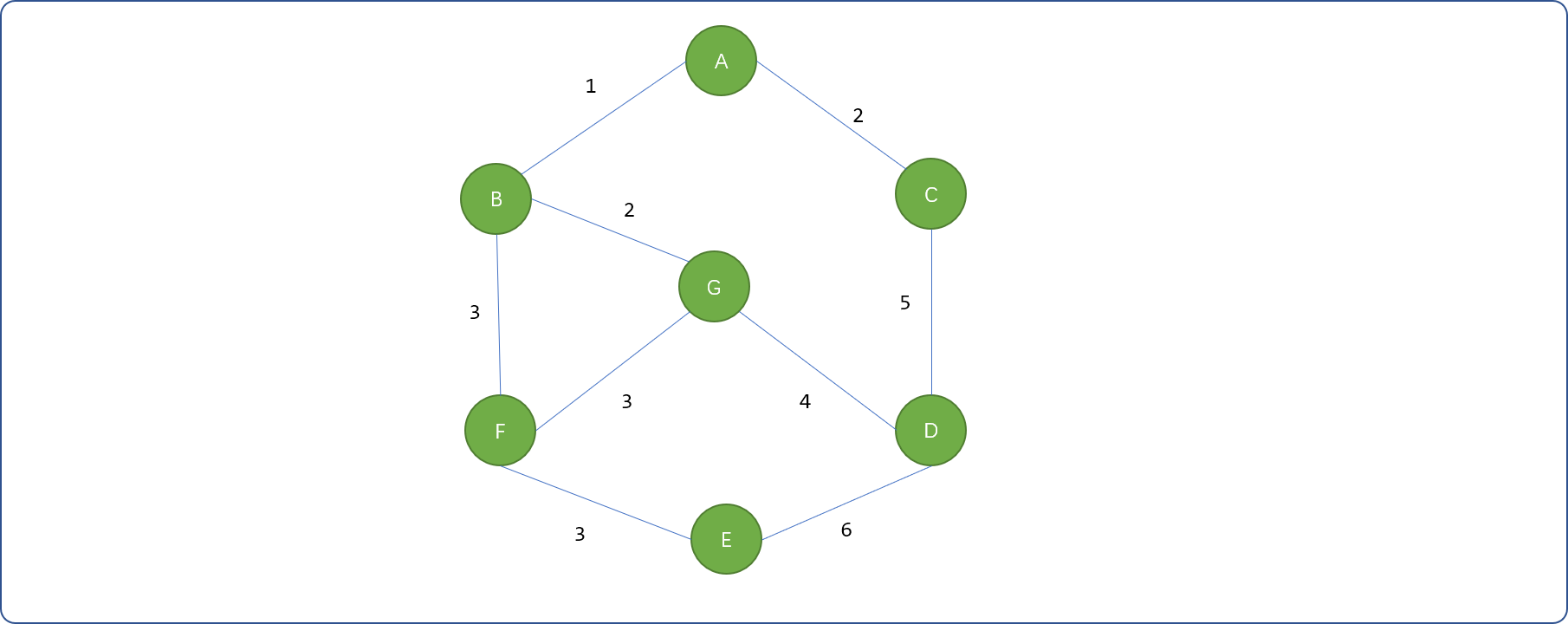
  • 任意选择一顶点，如A。然后把与此顶点相邻的边(A,B,1)、(A,C,2)压入到优先队列中，优先队列以边的权重小为优先。如下图所示。

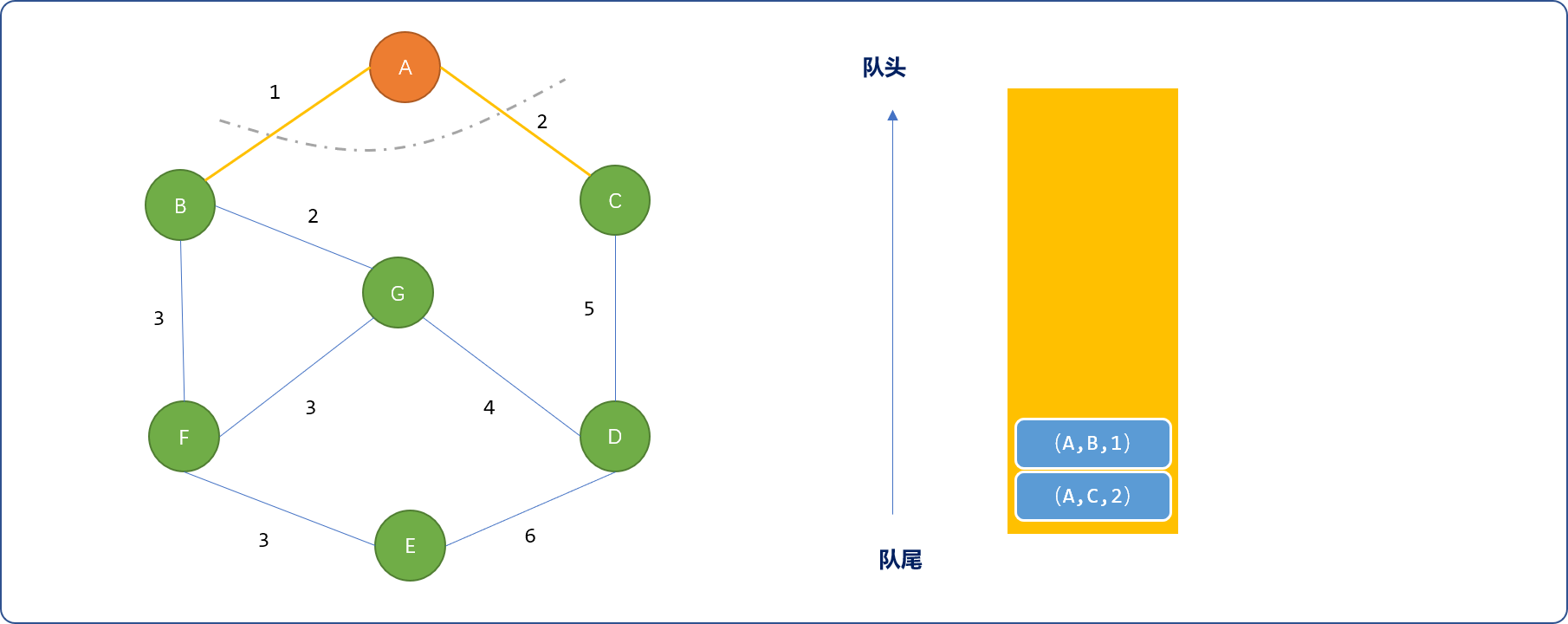
11.png

  • 从优先队列中选择(A,B,1)这条边，检查边两端的顶点是否已经被选择，选择B顶点。然后把B相邻的邻接边(B,G,2)、(B,F,3)压入到优先队列。

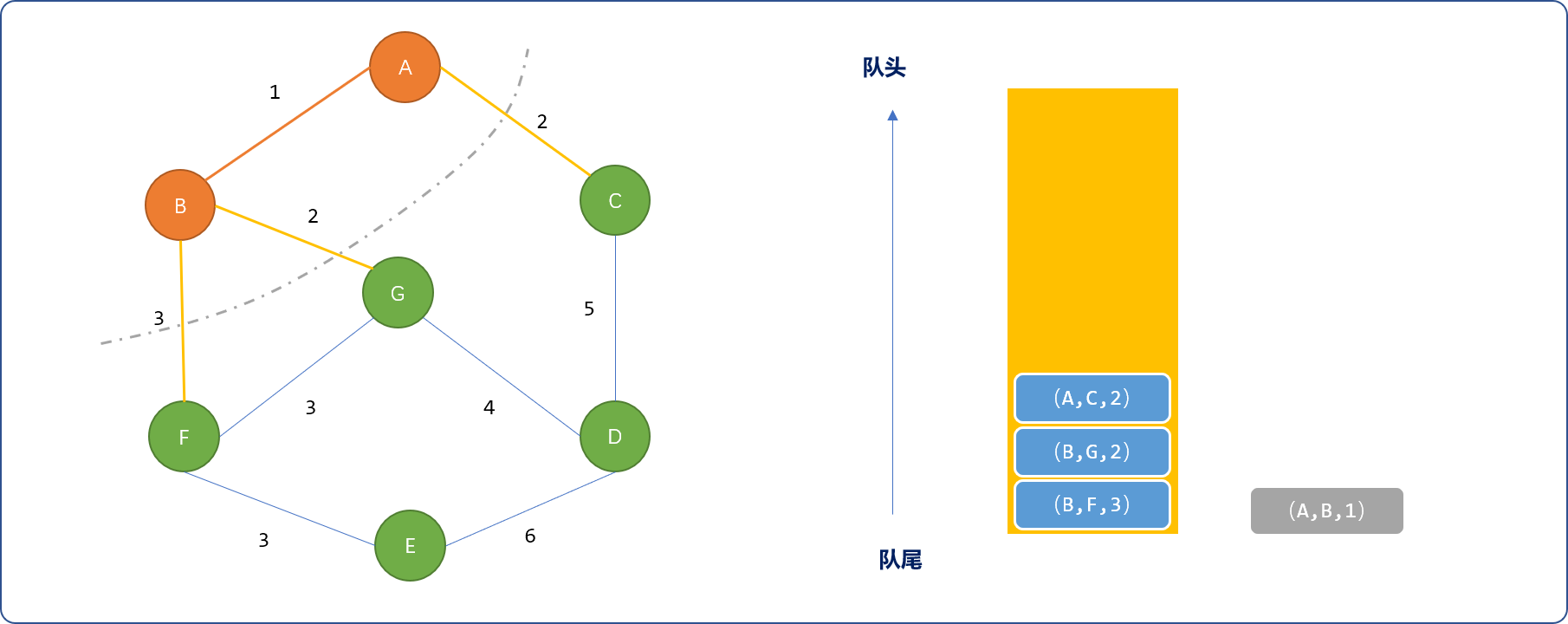
12.png

  • 从队列中选择(A,C,2)边，选择C顶点，且把C相邻边(C,D,5)压入队列。

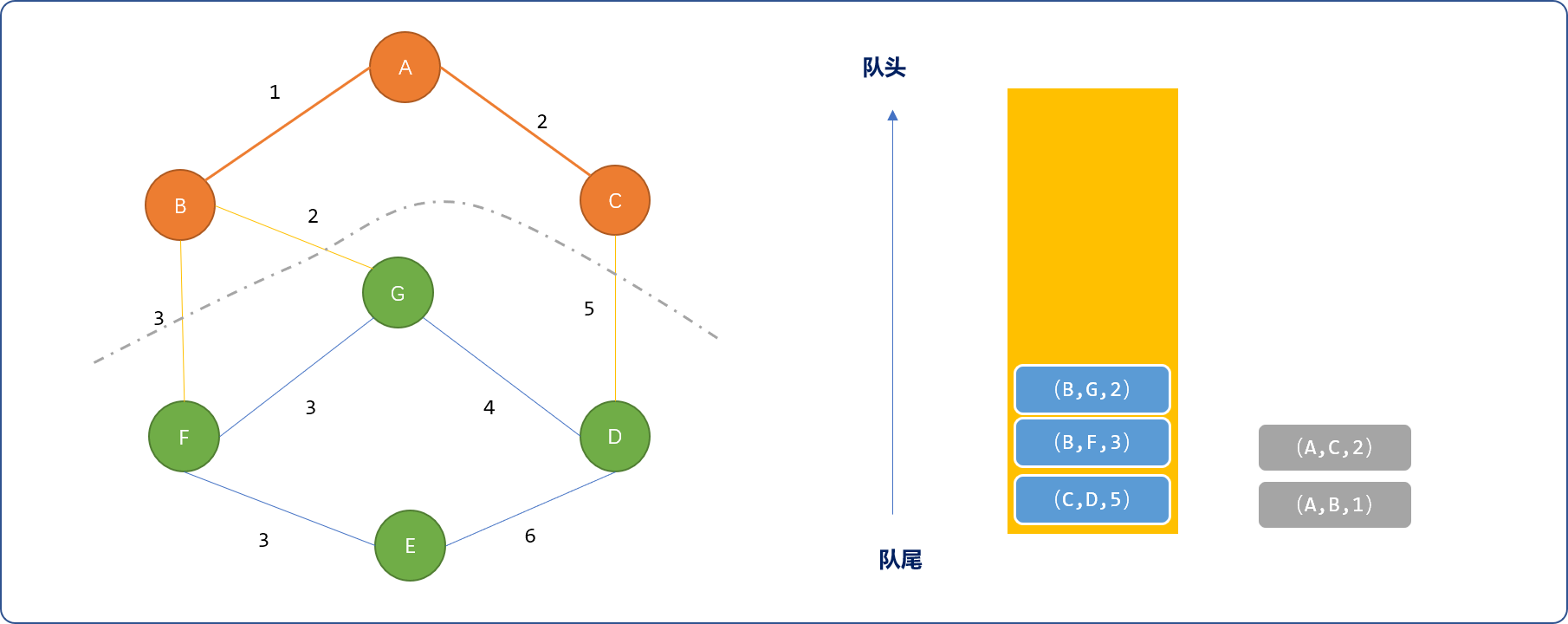
13.png

  • 选择（B,G,2）边，选择G顶点，且把(G,F,3)、(G,D,4)压入队列。

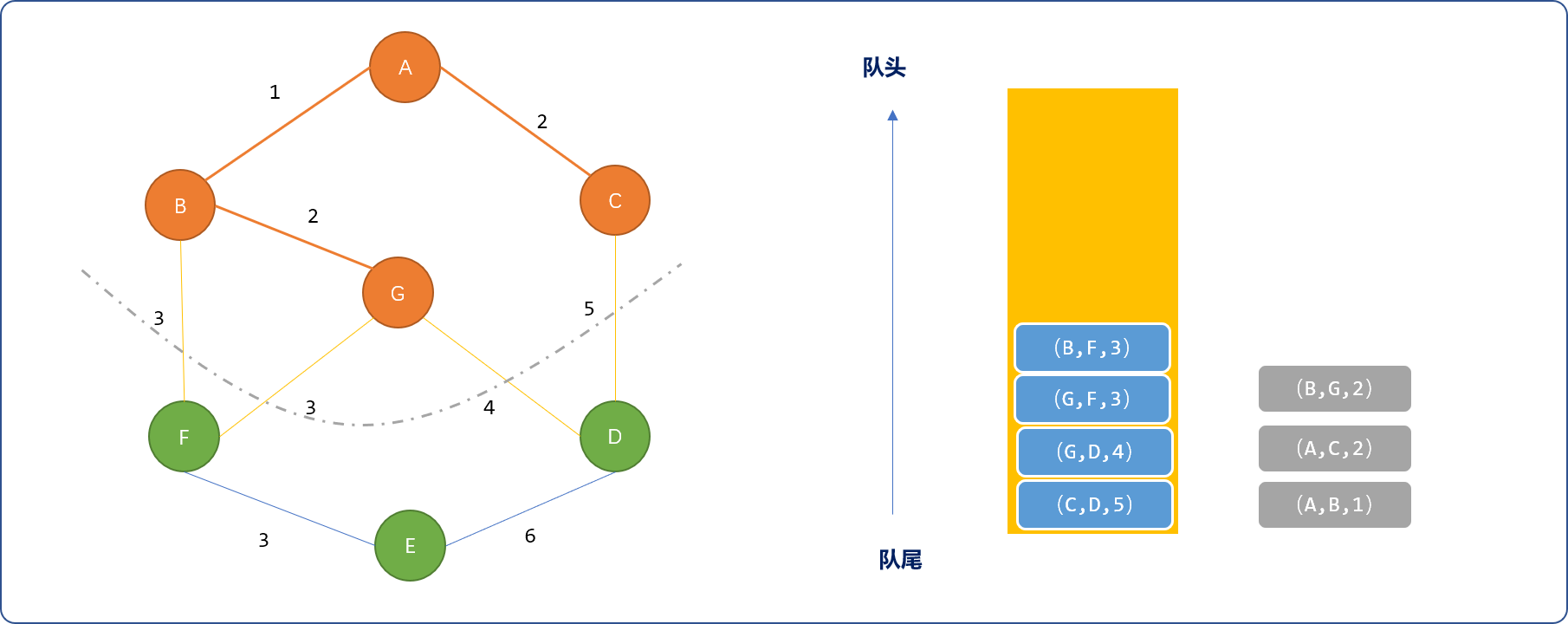
14.png

  • 从队列中选择(B,F,3)，选择F顶点，且压入(F,E,3)边。

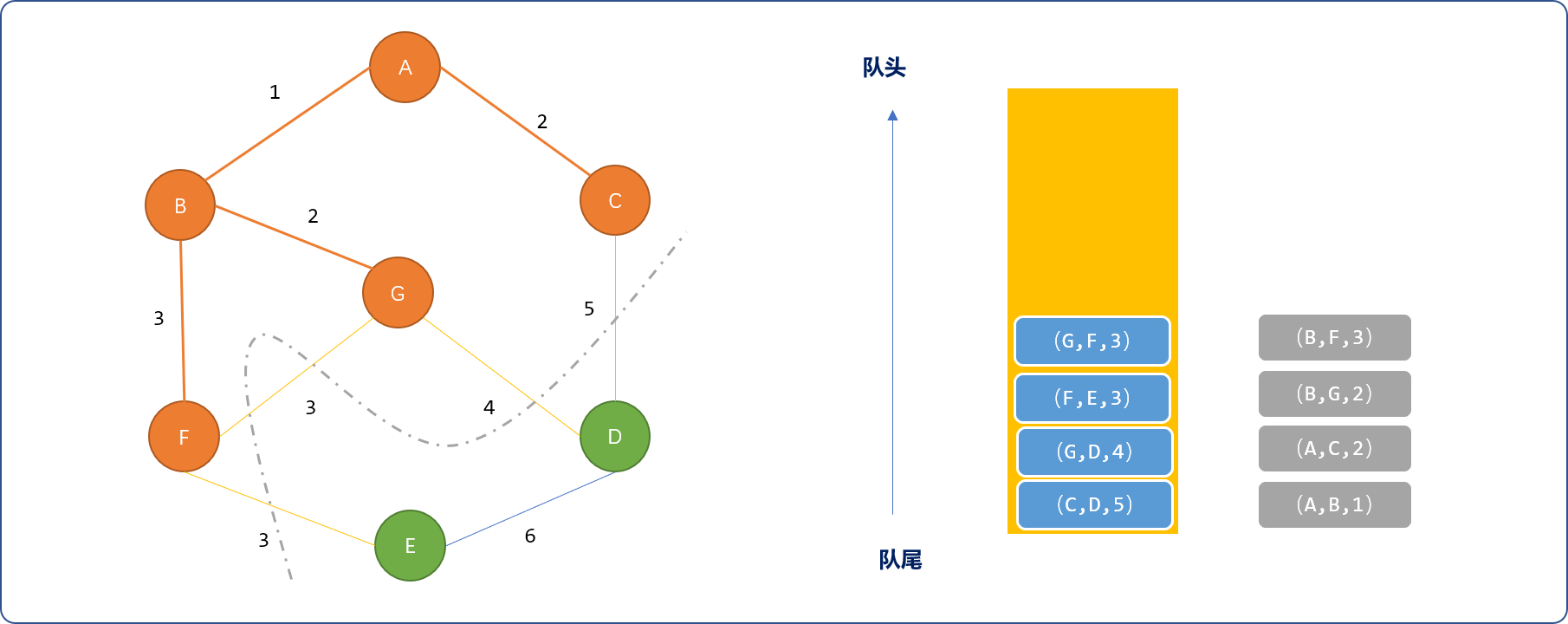
15.png

  • 选择(G,F,3)边，因边两端顶点都已经选择，再选择(F,E,3)边，选择E顶点，且把(E,d,6)压入队列。

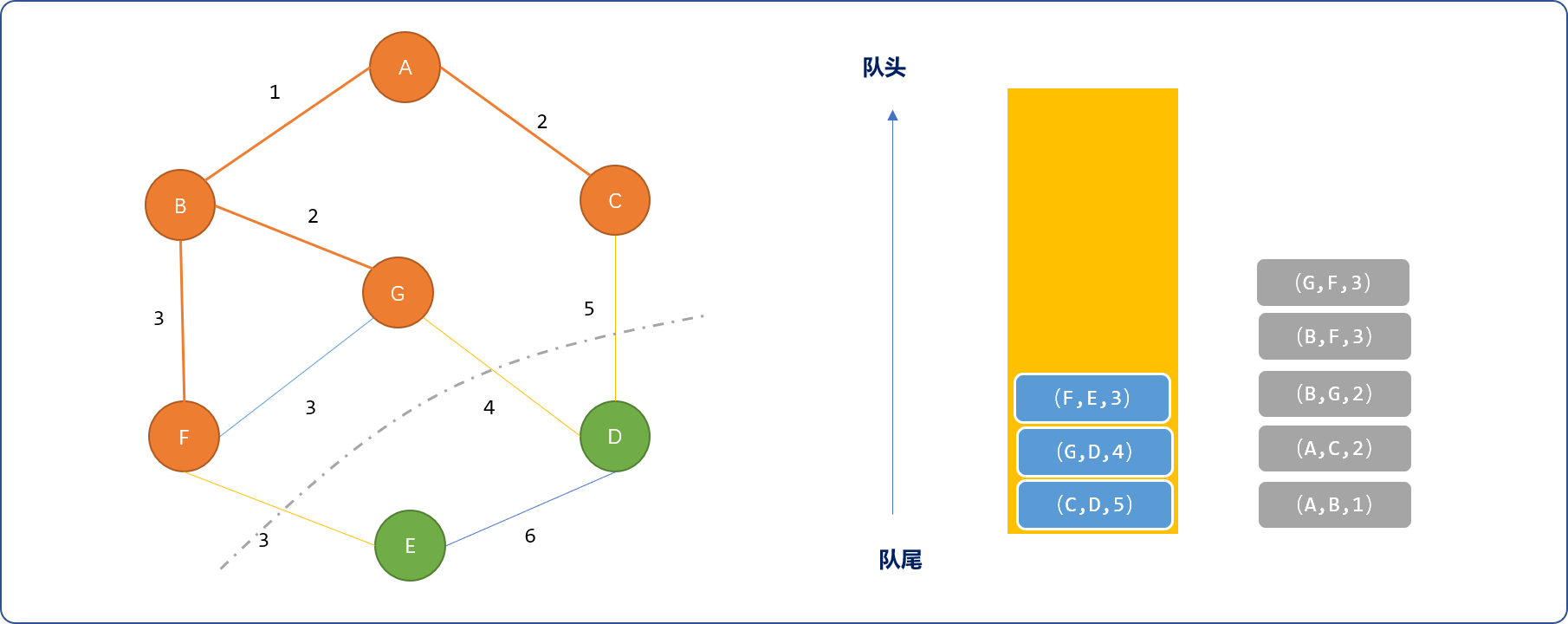
16.png

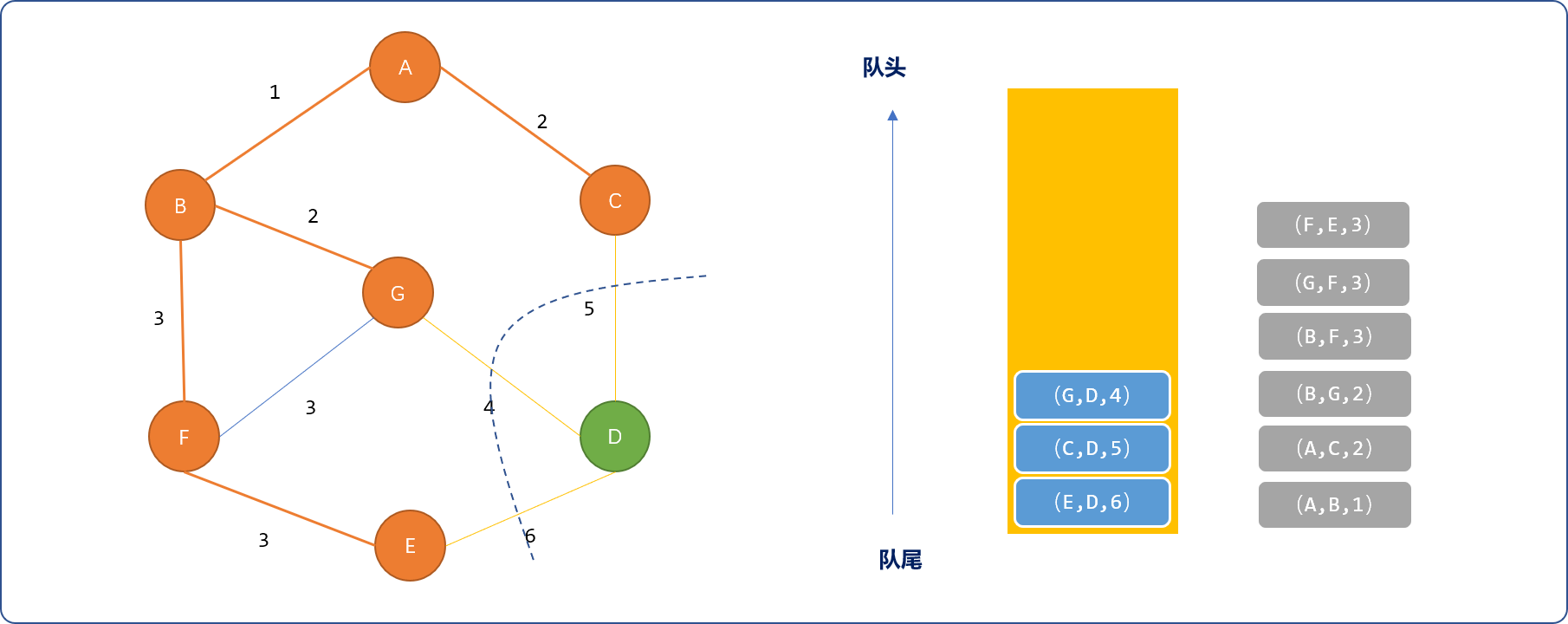
17.png

  • 最后选择(G,D,4)，选择D顶点，完成最小生成树。

18.png

3.2 编码实现

顶点类和树类和前面的kruskal算法一样。

因为需要动态获取边的权重，对边类升级：

template<typename T>
struct Edge {
	Vertex<T>* from;
	Vertex<T>* to;
	int weight;
	Edge() {}
	Edge(Vertex<T>* from,Vertex<T>* to,int weight) {
		this->from=from;
		this->to=to;
		this->weight=weight;
	}
    /*
    * 用于优先队列的比较法则
    */
	bool operator() (Edge<T>* v1, Edge<T>* v2) {
		//由小到大排列
		return v1->weight > v2->weight;
	}
};

Prim 算法类：

/*
*算法类
*/
template<typename T>
class Prim {
	private:
		//优先队列容器
		priority_queue<Edge<T>* ,vector<Edge<T>*>,Edge<T> > priorityQueue;
		//图的顶点
		map<int,Vertex<T>*> graph;
		//图的邻接矩阵
		int** martix;
		//图的顶点数量
		int size;
		//最小生成树
		Tree<T>* tree;
	public:
		/*
		*构造函数
		*/
		Prim(T data[],int** martix) {
			this->size= sizeof(data)/sizeof(T);
			//初始化图顶点
			for(int i=1; i<this->size; i++ ) {
				Vertex<T>* ver=new Vertex<T>(i,data[i]);
				this->graph[ver->code]=ver;
			}
			//初始化最小生成树
			this->tree=new Tree<T>( this->graph[1]);
            //图的邻接关系
			this->martix=martix;
		}
		/*
		*查找与某顶点邻接的边,并压入队列中
		*/
		void pushQueue(Vertex<T>* ver) {
			int row=ver->code;
			Vertex<T>* to=NULL;
			for(int i=1; i<this->size; i++) {
				if(this->martix[row][i]>0) {
					to=this->graph[i];
					Edge<T>* edge=new Edge<T>(ver,to,this->martix[row][i]);
					//添加边至队列
					this->priorityQueue.push(edge);
                     //标志已经使用
					this->martix[row][i]=0;
				}
			}
		}
		/*
		*核心
		*/
		void prim() {
			//得到最小生成树的根结点
			Vertex<T>* from= this->tree->getRoot();
			//找到邻接边
			this->pushQueue(from);
			while( !this->priorityQueue.empty() ) {
				//边出队列
				Edge<T>* edge = this->priorityQueue.top();
				this->priorityQueue.pop();
				//把结点添加至树中
				if(this->tree->addVertex(edge->from)) {
                      //查找相邻边
					this->pushQueue(edge->from);
				}
				if(this->tree->addVertex(edge->to)) {
					this->pushQueue(edge->to);
					edge->from->addChild(edge->to,edge->weight);
				}
			}
		}
		void showTree() {
			this->tree->showAll();
		}
};

测试

int main(int argc, char** argv) {
	char datas[8]= {'0','A','B','C','D','E','F','G'};
	//邻接矩阵存储顶点之间的关系
	int** martix=new int*[8];
	martix[0]=new int[8] {0,0,0,0,0,0,0,0};
	martix[1]=new int[8] {0,0,1,2,0,0,0,0};
	martix[2]=new int[8] {0,1,0,0,0,0,3,2};
	martix[3]=new int[8] {0,2,0,0,5,0,0,0};
	martix[4]=new int[8] {0,0,0,5,0,6,0,4};
	martix[5]=new int[8] {0,0,0,0,6,0,3,0};
	martix[6]=new int[8] {0,0,3,0,0,3,0,3};
	martix[7]=new int[8] {0,0,2,0,4,0,3,0};
	Prim<char> prim(datas,martix);
	prim.prim();
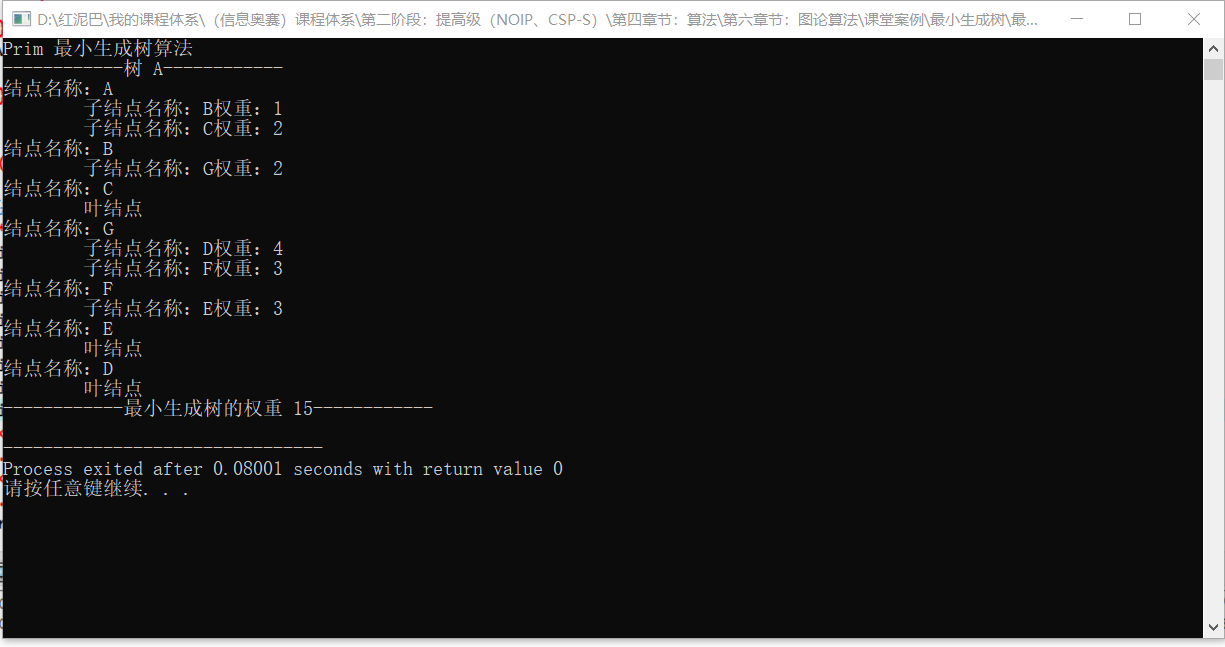
    cout<<"Prim 最小生成树算法"<<endl;
	prim.showTree();
	return 0;
}

输出结果：

19.png

4. 总结

kruskal和Prim算法有着同工异曲之地。都是使用贪心思想，保证在构建最小生成树时，每次获得到的权重都是最小的。区别再于，kruskal使用并查集保证顶点唯一性，Prim使用广度优先搜索。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/187719.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

esp32 烧录协议

esp32 烧录协议

esp32的rom固化了出场固件。进入烧录模式后&#xff0c;esp32串口输出&#xff1a;给esp32烧录固件的时候&#xff0c;需要和rom的bootloder进行通讯。通讯时&#xff0c;使用 SLIP 数据包帧进行双向数据传输。每个 SLIP 数据包都以 0xC0 开始和结束。 在数据包中&#xff0c;所…
阅读更多...
9、Servlet——Request对象

9、Servlet——Request对象

目录 一、get请求和post请求的区别 二、Request对象的应用 1、request主要方法 2、request获取数据 3、设置请求的编码格式 三、解决get请求收参乱码问题 四、解决post请求中文乱码问题 一、get请求和post请求的区别 在Servlet中用来处理客户端请求需要用doGet()方法或…
阅读更多...
openGauss数据库源码解析系列文章——备份恢复机制：openGauss全量备份技术

openGauss数据库源码解析系列文章——备份恢复机制：openGauss全量备份技术

目录 10.1 openGauss全量备份技术 10.1.1 gs_basebackup备份工具 10.1.2 gs_basebackup备份交互流程 本文主要介绍openGauss的备份恢复原理和技术。备份恢复是数据库日常维护的一个例行活动&#xff0c;通过把数据库数据备份到另外一个地方&#xff0c;可以抵御介质类的损…
阅读更多...
数据结构与算法-稀疏数组

数据结构与算法-稀疏数组

Java高级系列文章前言 本文章涉及到数据结构与算法的知识&#xff0c;该知识属于Java高级阶段&#xff0c;通常为学习的二阶段&#xff0c;本系列文章涉及到的内容如下&#xff08;橙色框选内容&#xff09;&#xff1a; 本文章核心是教学视频&#xff0c;所以属于个人笔记&a…
阅读更多...
深度卷积对抗神经网络 基础 第六部分 缺点和偏见 GANs Disadvantages and Bias

深度卷积对抗神经网络 基础 第六部分 缺点和偏见 GANs Disadvantages and Bias

深度卷积对抗神经网络 基础 第六部分 缺点和偏见 GANs Disadvantages and Bias GANs 综合评估 生成对抗网络&#xff08;英语&#xff1a;Generative Adversarial Network&#xff0c;简称GAN&#xff09;是非监督式学习的一种方法&#xff0c;透过两个神经网络相互博弈的方式…
阅读更多...
实体对齐（三）：RNM

实体对齐（三）：RNM

一.摘要 实体对齐旨在将来自不同知识图&#xff08;KG&#xff09;的具有相同含义的实体联系起来&#xff0c;这是知识融合的重要步骤。 现有研究侧重于通过利用知识图谱的结构信息学习实体嵌入来进行实体对齐。这些方法可以聚合来自相邻节点的信息&#xff0c;但也可能带来来…
阅读更多...
从软件开发角度看待PCI和PCIe

从软件开发角度看待PCI和PCIe

从软件开发角度看待PCI和PCIe 文章目录从软件开发角度看待PCI和PCIe参考资料&#xff1a;一、 最容易访问的设备是什么二、 地址空间的概念三、 理解PCI和PCIE的关键3.1 地址空间转换3.2 PCI接口速览3.3 PCIe接口速览四、 访问PCI/PCIe设备的流程4.1 PCI/PCIe设备的配置信息4.2…
阅读更多...
特斯拉2022全年财报摘要

特斯拉2022全年财报摘要

重点一览一、盈利方面 2022全年营业利润率为16.8%&#xff0c;其中第四季度为16.0% 2022全年GAAP营业利润为137亿美元&#xff0c;其中第四季度为39亿美元 2022全年GAAP净利润为126亿美元&#xff0c;其中第四季度为37亿美元 2022全年非GAAP净利润为141亿美元&#xff0c;其中…
阅读更多...
MySQL中的多表联合查询

MySQL中的多表联合查询

目录 一.介绍 数据准备 交叉连接查询 内连接查询 外连接 子查询 特点 子查询关键字 all关键字 any关键字和some关键字 in关键字 exists关键字 自关联查询 总结 一.介绍 多表查询就是同时查询两个或两个以上的表&#xff0c;因为有的时候用户在查看数据的时候,需要…
阅读更多...
四足机器人发展史及机器人盘点

四足机器人发展史及机器人盘点

四足机器人发展史及机器人盘点 本文翻译整理自文章 四足行走机器人发展综述 20世纪初前后 1870 CHebyshev(沙俄)发明了第一个行走机构, 将旋转运动转换为匀速平动运动. - 由于连接机构形似希腊字母λ, 该连杆命名为λ机构. - 可在平面运动, 没有独立的腿部运动 - Rygg(美国…
阅读更多...
windows下nodejs下载及环境变量配置，运行vue项目

windows下nodejs下载及环境变量配置，运行vue项目

文章目录1.下载安装node.js2.环境变量配置&#xff08;重点&#xff09;3.切换镜像源切换yarn作为主力命令1.下载安装node.js 1.https://registry.npmmirror.com/binary.html 搜索node&#xff0c;下载对应的版本&#xff0c;安装即可。一路next&#xff0c;路径选择自己想放置…
阅读更多...
与string容易混淆的类——StringBuilder

与string容易混淆的类——StringBuilder

目录 StringBuilder类概述及其构造方法 StringBuilder类的常用方法 StringBuilder类练习 StringBuilder类概述及其构造方法 StringBuilder类概述–我们如果对字符串进行拼接操作&#xff0c;每次拼接&#xff0c;都会构建一个新的String对象&#xff0c;既耗时&#xff0c;…
阅读更多...
verilog图像算法实现与仿真（流程和实现）

verilog图像算法实现与仿真（流程和实现）

【声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 前面我们谈到了fpga&#xff0c;谈到了用pythoncv2实现图像算法&#xff0c;直到现在才算是慢慢进入了正题。毕竟用verilog实现图像算法&#xff0c…
阅读更多...
HalfEdge半边数据结构详解

HalfEdge半边数据结构详解

我们可以将离散表面表示为多边形网格。 多边形网格可以被认为是图&#xff08;具有顶点和顶点之间的边&#xff09;加上面列表&#xff0c;其中面是边的环。 推荐&#xff1a; 使用 NSDT场景设计器 快速搭建 3D场景。 下面&#xff0c;我们将网格指定为顶点列表和面列表&#…
阅读更多...
【博学谷学习记录】大数据课程-学习第四周总结

【博学谷学习记录】大数据课程-学习第四周总结

分布式技术 为什么需要分布式 计算问题 无论是我们在学校刚开始学编程&#xff0c;还是在刚参加工作开始处理实际问题&#xff0c;写出来的程序都是很简单的。因为面对的问题很简单。以处理数据为例&#xff0c;可能只是把一个几十K的文件解析下&#xff0c;然后生成一个词频…
阅读更多...
Python正则表达式所有函数详解

Python正则表达式所有函数详解

文章目录1 fullmatch2 match3 search4 findall5 finditer6 split7 sub8 compile本篇博客主要讲解正则表达式相关的函数&#xff0c;均不涉及复杂的正则表达式语法。如需了解正则表达式语法&#xff0c;请参考下面的文章&#xff1a;Python正则表达式语法详解1 fullmatch Pytho…
阅读更多...
96. BERT预训练代码

96. BERT预训练代码

利用实现的BERT模型和从WikiText-2数据集生成的预训练样本&#xff0c;我们将在本节中在WikiText-2数据集上对BERT进行预训练。 import torch from torch import nn from d2l import torch as d2l首先&#xff0c;我们加载WikiText-2数据集作为小批量的预训练样本&#xff0c;…
阅读更多...
Logstash：如何使用 Logstash 解析并摄入 JSON 数据到 Elasticsearch

Logstash：如何使用 Logstash 解析并摄入 JSON 数据到 Elasticsearch

在我之前的文章 “Logstash&#xff1a;Data 转换&#xff0c;分析&#xff0c;提取&#xff0c;丰富及核心操作” 有涉及到这个话题。今天我想使用一个具体的例子来更深入地展示。 准备数据 我们先来把如下的数据拷贝下来&#xff0c;并保存到一个叫做 sample.json 的文件中。…
阅读更多...
OS 学习笔记(5) 操作系统的体系结构

OS 学习笔记(5) 操作系统的体系结构

OS 学习笔记(5) 操作系统的体系结构 王道OS 1.4 操作系统的体系结构 文章目录OS 学习笔记(5) 操作系统的体系结构知识总览分层结构模块化操作系统的内核大内核 vs 微内核知识回顾与重要考点外核王道chap1 回顾英文表达、术语积累&#xff08;《操作系统概念》第九版、ostep 《O…
阅读更多...
电子模块|心率血氧传感器模块MAX30102及其驱动代码

电子模块|心率血氧传感器模块MAX30102及其驱动代码

电子模块|心率血氧传感器模块MAX30102及其驱动代码实物照片模块简介工作原理原理图及引脚说明STM32软件驱动IIC通信代码数值转换代码main函数结果实物照片 模块简介 MAX30102是一个集成的脉搏血氧仪和心率监测仪生物传感器的模块。 它集成了一个红光LED和一个红外光LED、光电…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023