Java高级系列文章前言
本文章涉及到数据结构与算法的知识,该知识属于Java高级阶段,通常为学习的二阶段,本系列文章涉及到的内容如下(橙色框选内容):
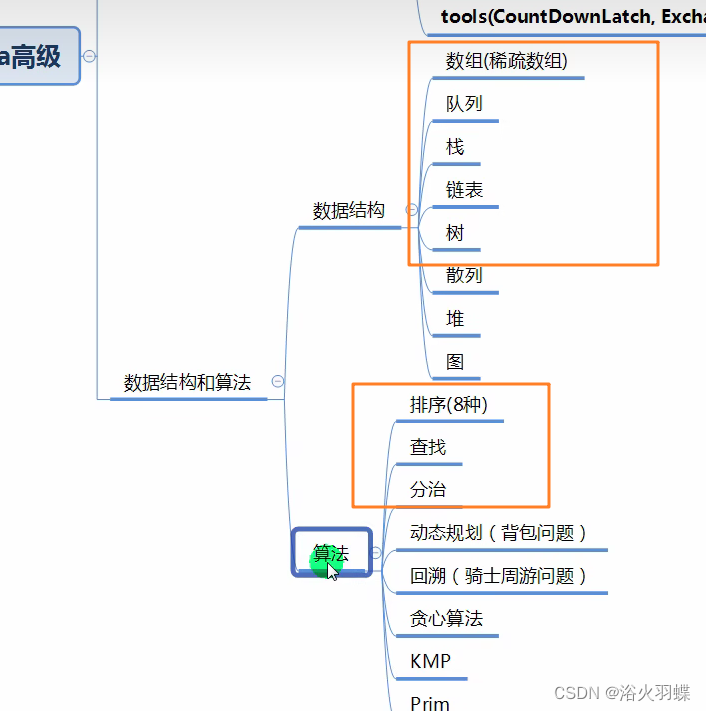
本文章核心是教学视频,所以属于个人笔记,非商用。
文章结构
标识
本系列文章中记录的数据结构与算法都会多多少少用到一些Java的API,这些API只会一笔带过,主要还是看逻辑思路。
大标题
小标题
文本内容和图片内容... 70%/30%
图片说明(加重)
逻辑思路和次要说明
文本说明(普通文本)
主要说明和补充
内容结构
大标题
介绍
英文单词关键字陈列(有时会省略)
代码块...
思路引入
思路解析
源码
代码展示 二级标题
图文说明 二级标题
稀疏数组
介绍
稀疏数组的思路是保存数组中有效数据的行索引、列索引和值,记录数组一共有几行几列,有多少个不同的值,把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模。
英文单词关键字陈列
书写习惯:XxxYyyZzz(Java类驼峰语法)
格式:英文单词 -> 中文翻译 -> 空耳(个人习惯)
SparseArray -> 稀疏数组 -> 死怕死阿瑞
Chess -> 棋盘 -> 拆死
Recovery -> 恢复 -> 瑞卡佛瑞
思路引入
假设我们创建了一个二维数组,该二维数组是11*11大小,整形类型的,默认值为0,所以就呈现为一个11*11的抽象二维棋盘(由0组成的矩阵棋盘)。
如果下面棋盘是一个五子棋游戏,那么该游戏有存盘和读盘的功能,我们需要保存用户下棋的位置,并且下次用户读取进度时进行恢复,那么因为二维数组默认值是0,可以说很多地方都是0,我们如果全部保存棋盘位置,则非常浪费空间和资源,因为保存默认值是没有意义的,我们需要只保存用户下棋的位置,然后用保存的位置来恢复先前进度。
二维数组组成的棋盘
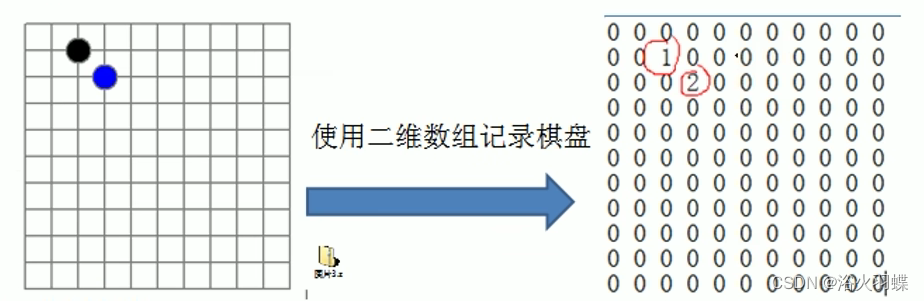
思路解析
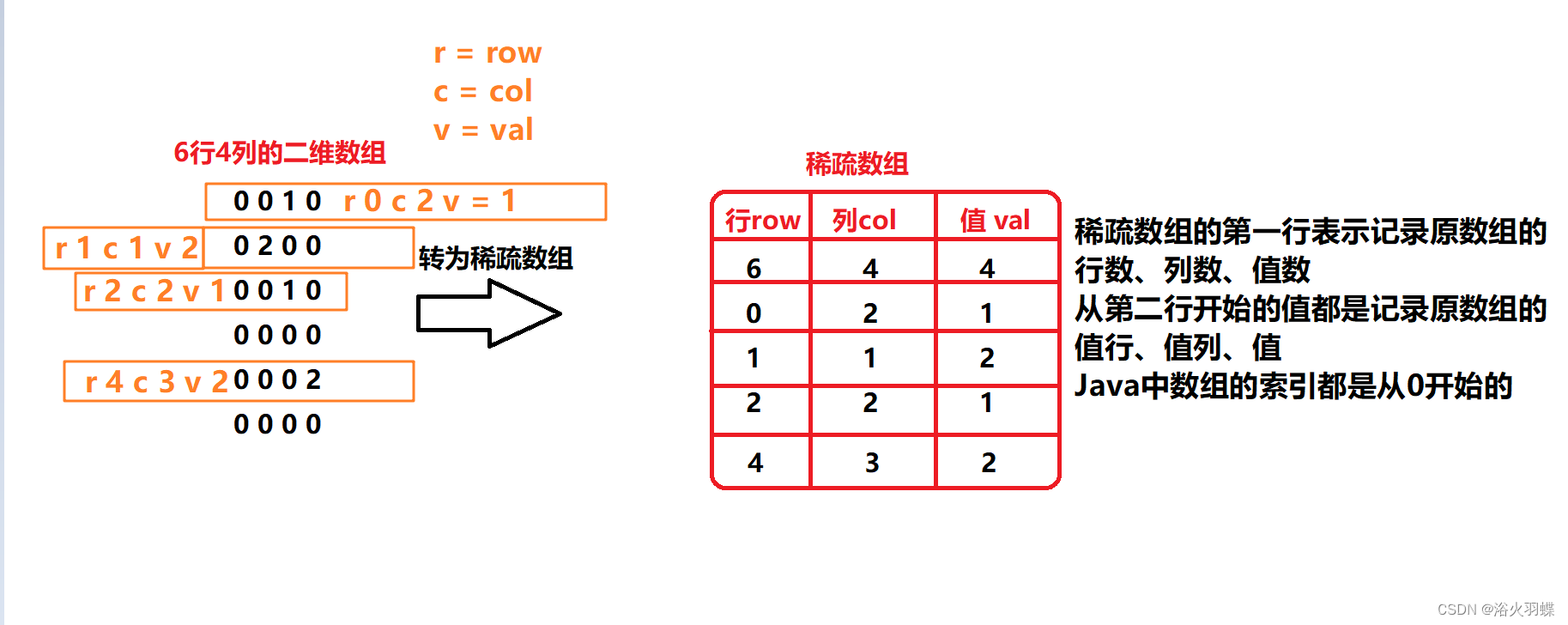
我们可以提取出棋盘上不为0的值,此处假设为只有1和2是和0不同的值,我们只保存1和2,将1和2保存到另一个数组中,我们可以使用新数组来记录原数组的行、列和有多少个不为0的值。
新数组的第一列表示原数组行、第二列表示原数组列、第三列表示原数组的元素值。
此处我们新数组是要记录原数组的行、列、值总量,所以新数组的第一行保存的是:原数组行大小、原数组列大小、原数组不为0的值的个数。
从第二行开始,就是记录不为0的值在原数组几行几列什么值。
稀疏数组是一个固定的三列数组,其行数并不固定,第一行是必有的。
三列:1->原数组行数 2->原数组列数 3->原数组值数
1.初始化的二维数组棋盘

2.转为稀疏数组
源码
代码展示
package SparseArray;
public class SparseArray {
public static void main(String[] args) {
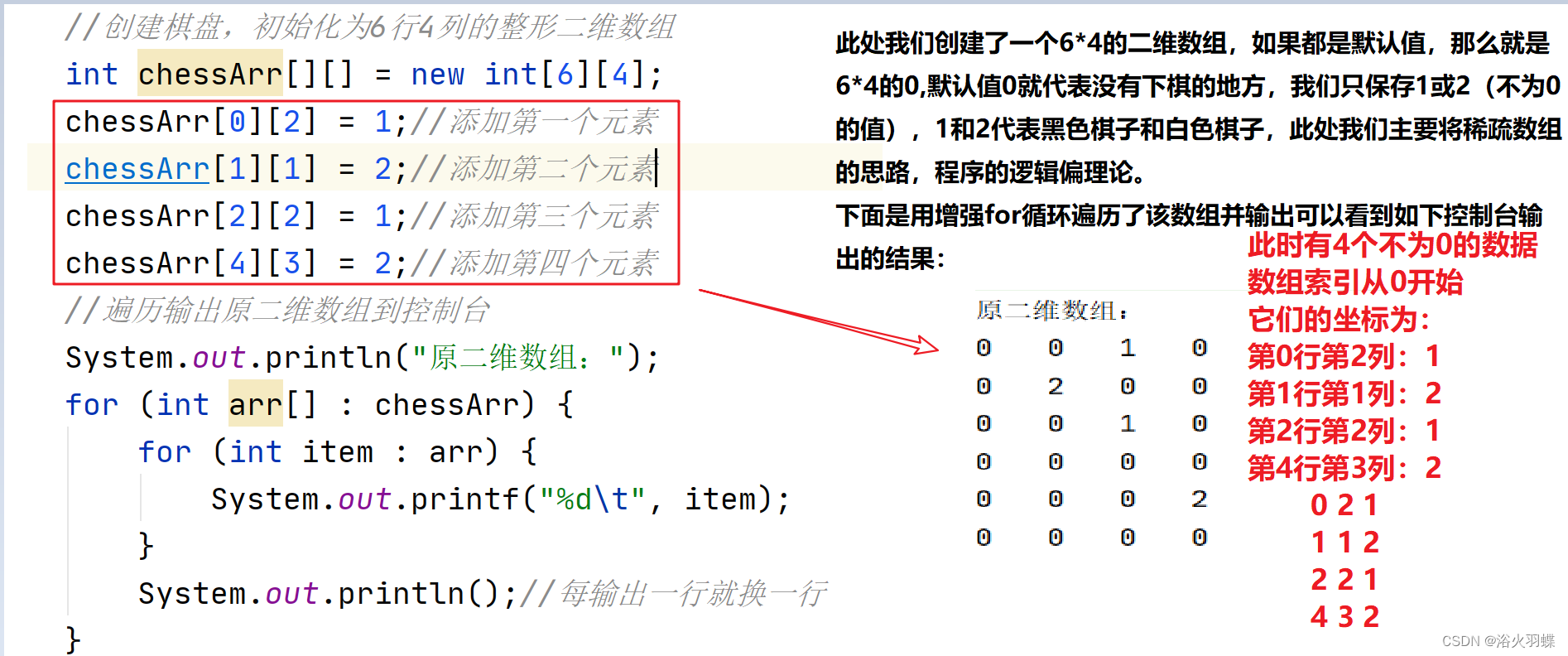
//创建棋盘,初始化为6行4列的整形二维数组
int chessArr[][] = new int[6][4];
chessArr[0][2] = 1;//添加第一个元素
chessArr[1][1] = 2;//添加第二个元素
chessArr[2][2] = 1;//添加第三个元素
chessArr[4][3] = 2;//添加第四个元素
//遍历输出原二维数组到控制台
System.out.println("原二维数组:");
for (int arr[] : chessArr) {
for (int item : arr) {
System.out.printf("%d\t", item);
}
System.out.println();//每输出一行就换一行
}
//将原二维数组转换为稀疏数组
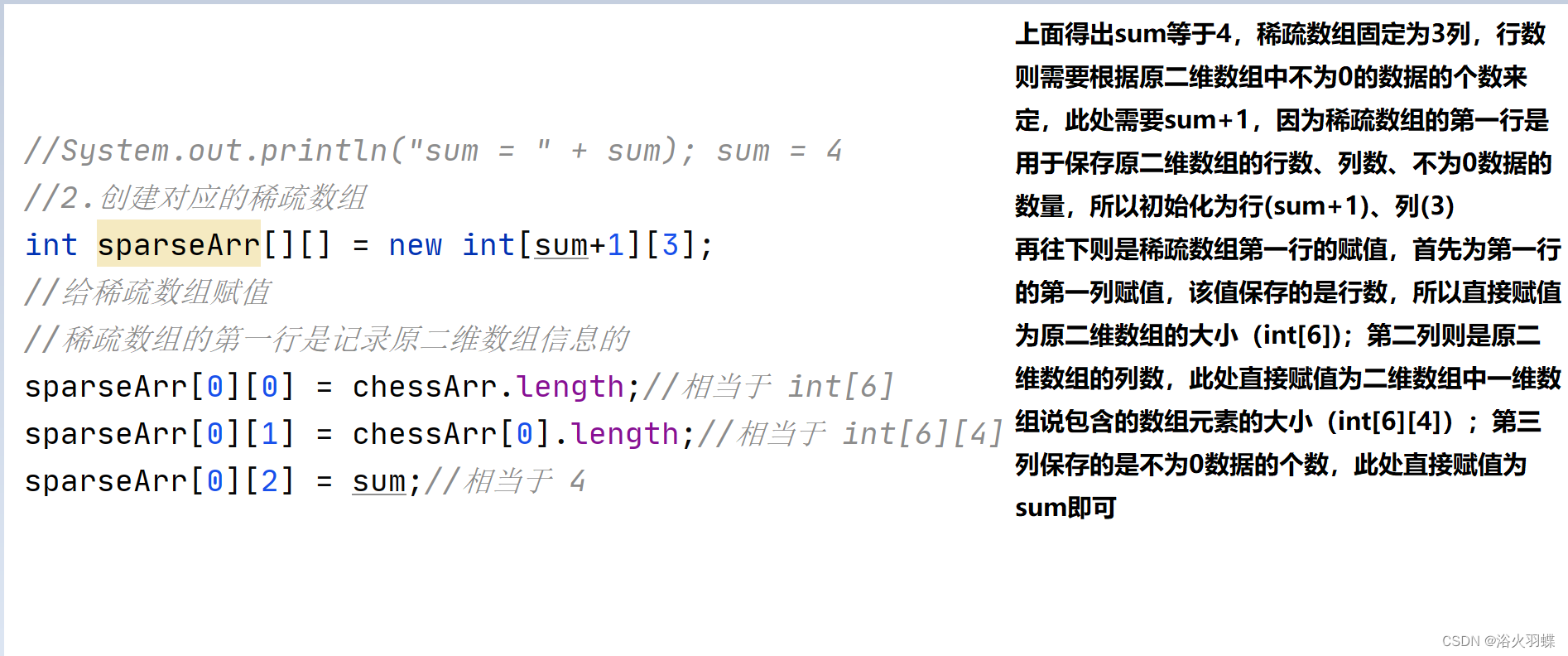
//1.先遍历出不为0的值的数量
int sum = 0;//用于记录原二维数组中非0值的数量 该变量值为稀疏数组的行数
for (int i = 0; i < chessArr.length; i++) {
for (int j = 0; j < chessArr[i].length;j++) {
if (chessArr[i][j] != 0) {//遍历到不为0的值就让sum自增1
sum++;
}
}
}
//System.out.println("sum = " + sum); sum = 4
//2.创建对应的稀疏数组
int sparseArr[][] = new int[sum+1][3];
//给稀疏数组赋值
//稀疏数组的第一行是记录原二维数组信息的
sparseArr[0][0] = chessArr.length;//相当于 int[6]
sparseArr[0][1] = chessArr[0].length;//相当于 int[6][4]
sparseArr[0][2] = sum;//相当于 4
//遍历二维数组,将非0的值存放到稀疏数组中
//创建一个变量,用于记录存到稀疏数组中第几个非0数据
int count = 0;//
for (int i = 0; i < chessArr.length; i++) {
for (int j = 0; j < chessArr[i].length;j++) {
if (chessArr[i][j] != 0) {//遍历到不为0的值就保存到稀疏数组中
count++;//表示遍历到了一个非0的数据,直接自增一次,然后开始执行添加
sparseArr[count][0] = i;//i表示的是当前循环到的行数
sparseArr[count][1] = j;//i表示的是当前循环到的列数
sparseArr[count][2] = chessArr[i][j];//表示的是当前循环到的元素值
}
}
}
System.out.println("=====分割线=====");
System.out.println("稀疏数组:");
System.out.println("行\t列\t值\t");//表头
//遍历输出原二维数组到控制台
for (int arr[] : sparseArr) {
for (int item : arr) {
System.out.printf("%d\t", item);
}
System.out.println();//每输出一行就换一行
}
System.out.println("=====分割线=====");
//将稀疏数组恢复成原二维数组
int recoveryArrRow = sparseArr[0][0];
int recoveryArrCol = sparseArr[0][1];
int recoveryArr[][] = new int[recoveryArrRow][recoveryArrCol];
//输出初始化后的恢复数组(无数据,但大小恢复了)
System.out.println("恢复原二维数组(无数据):");
for (int arr[] : recoveryArr) {
for (int item : arr) {
System.out.printf("%d\t", item);
}
System.out.println();//每输出一行就换一行
}
System.out.println("=====分割线=====");
for (int i = 1; i < sparseArr.length; i++){//从稀疏数据的第二行开始遍历,因为第一行保存的是信息
recoveryArr[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
//再次遍历,此时是恢复了数据的数组
System.out.println("恢复后的原二维数组:");
for (int arr[] : recoveryArr) {
for (int item : arr) {
System.out.printf("%d\t", item);
}
System.out.println();//每输出一行就换一行
}
}
}
图文说明
1.创建原二维数组和添加一些数据
2.遍历得出不为0数据的个数并初始化稀疏数组

3.将不为0的数据添加到稀疏数组中
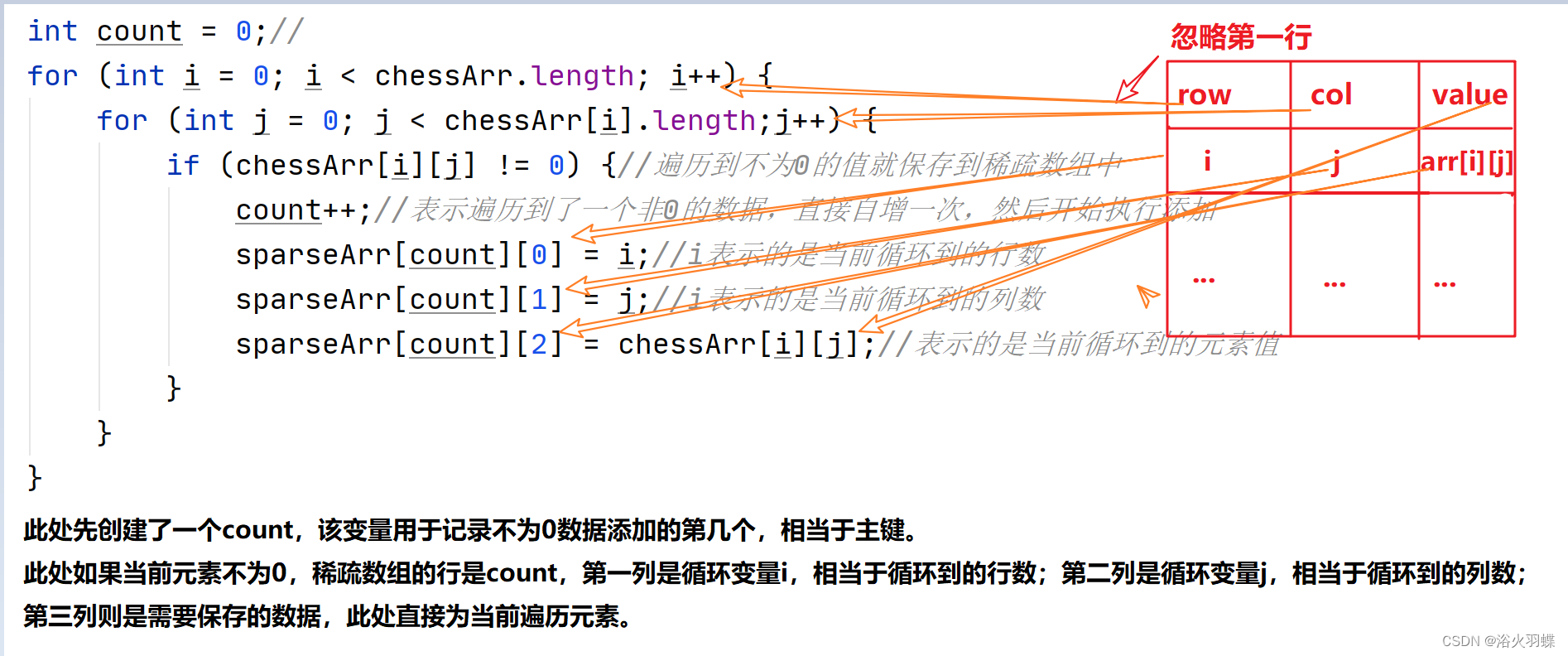
此处遍历输出忽略,上面源码中有写。
4.将稀疏数组恢复成原二维数组(无数据)

5.将稀疏数组恢复成原二维数组
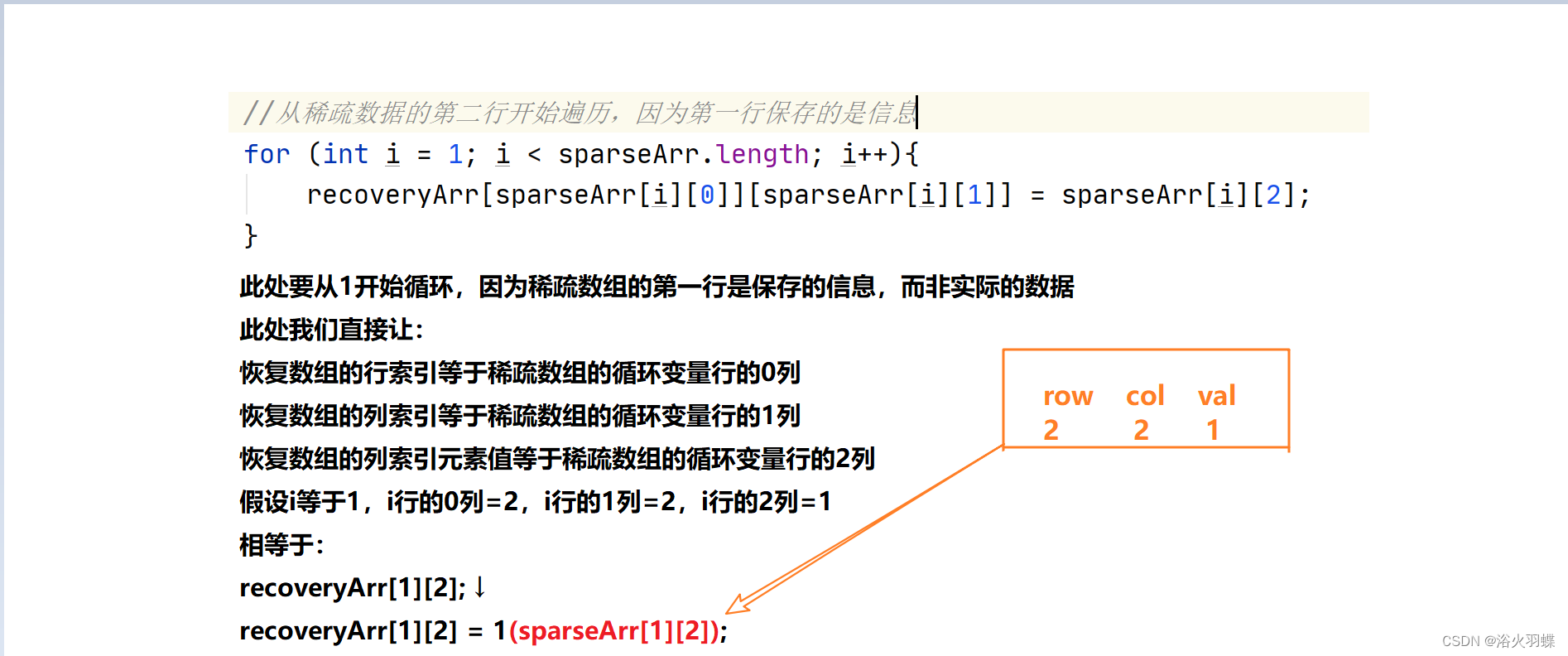
此处遍历输出忽略,上面源码中有写。