一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

目录

我的写法

代码点评

时间复杂度分析

空间复杂度分析

总结

我要更强

优化建议

优化后的代码

代码注释

时间复杂度和空间复杂度分析

哲学和编程思想

抽象与封装：

效率与优化：

简洁与清晰：

不变性与可变性：

DRY原则（Don't Repeat Yourself）：

KISS原则（Keep It Simple, Stupid）：

YAGNI原则（You Ain't Gonna Need It）：

单一职责原则（Single Responsibility Principle）：

开闭原则（Open/Closed Principle）：

举一反三

---

题目链接：https://pintia.cn/problem-sets/994805260223102976/exam/problems/type/7?problemSetProblemId=994805263964422144&page=0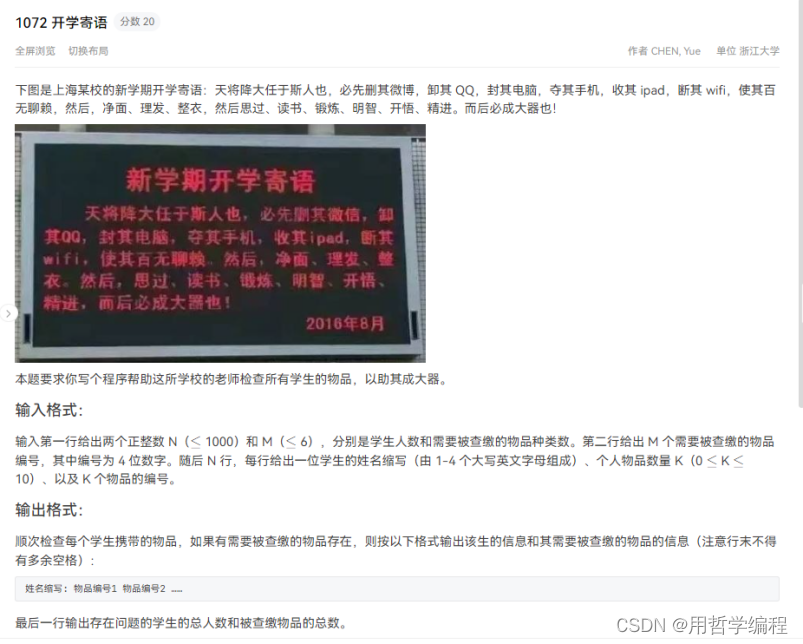

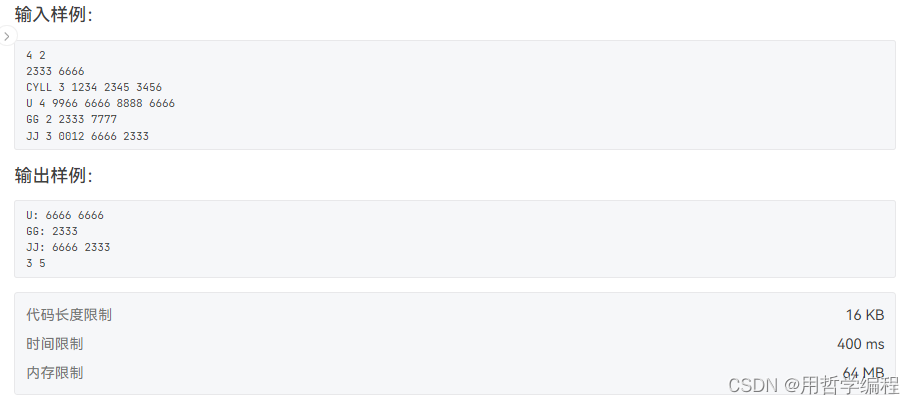
我的写法

inputs=input().split()
n=int(inputs[0])
m=int(inputs[1])

forbid_items=input().split()
out_stu_num=0
out_item_num=0


for i in range(n):
    inputs=input().split()
    name=inputs[0]
    person_items=inputs[2:]
    tmp=[]
    
    for person_item in person_items:
        if person_item not in forbid_items:
            tmp.append(person_item)

    for i in tmp:
        person_items.remove(i)

    if person_items:
        print(f"{name}:",end='')
        for person_item in person_items:
            print(f" {person_item}",end='')
        print()
        out_stu_num+=1
        out_item_num+=len(person_items)
        

print(f"{out_stu_num} {out_item_num}")

这段代码的功能是处理学生携带物品的问题。具体来说，它读取学生数量 n 和禁止携带的物品数量 m，然后读取禁止携带的物品列表。接着，对于每个学生，它读取学生的姓名和携带的物品，并检查这些物品是否在禁止携带的物品列表中。如果是，则输出该学生的姓名和禁止携带的物品，并记录违规的学生数量和物品数量。

代码点评

1. 输入处理：
   • 代码使用了 input().split() 来读取输入，这是一种常见的处理方式。
   • 通过 int(inputs[0]) 和 int(inputs[1]) 分别获取学生数量 n 和禁止携带的物品数量 m，这是合理的。
2. 数据结构：
   • 使用列表 forbid_items 来存储禁止携带的物品，这是合适的选择。
   • 使用 person_items 来存储每个学生携带的物品，这也是合适的选择。
3. 逻辑处理：
   • 代码通过嵌套的 for 循环来检查每个学生携带的物品是否在禁止携带的物品列表中。
   • 使用 tmp 列表来存储允许携带的物品，然后从 person_items 中移除这些物品，这是一种有效的方法。
4. 输出处理：

• 代码通过 print 函数输出违规学生的姓名和物品，格式化输出是合理的。
• 最后输出违规学生的总数和物品总数，这也是合理的。

时间复杂度分析

• 输入处理：读取输入的时间复杂度是 O(n + m)。
• 检查物品：对于每个学生，检查每个物品是否在禁止携带的物品列表中的时间复杂度是 O(n * k)，其中 k 是每个学生携带的物品数量。
• 移除物品：从 person_items 中移除物品的时间复杂度是 O(k)。

综合来看，整体时间复杂度是 O(n * k)，其中 k 是每个学生携带的物品数量的平均值。

空间复杂度分析

• 输入存储：存储学生数量 n 和禁止携带的物品数量 m 的空间复杂度是 O(1)。
• 禁止携带物品列表：存储禁止携带的物品列表的空间复杂度是 O(m)。
• 学生携带物品列表：存储每个学生携带的物品列表的空间复杂度是 O(n * k)。

综合来看，整体空间复杂度是 O(m + n * k)。

总结

• 优点：代码结构清晰，逻辑处理合理，能够正确处理输入并输出结果。
• 缺点：在移除物品时，使用 person_items.remove(i) 可能会导致线性时间复杂度，因为列表的 remove 操作是 O(k) 的。可以考虑使用集合（set）来优化这一部分。

改进建议：可以使用集合（set）来存储禁止携带的物品列表，这样可以优化检查物品是否在禁止携带列表中的时间复杂度。同时，可以使用集合来存储每个学生携带的物品，以优化移除物品的操作。

---

我要更强

优化时间复杂度和空间复杂度的方法通常涉及使用更高效的数据结构和算法。以下是一些优化建议，并附上相应的代码和注释。

优化建议

1. 使用集合（Set）：
   • 使用集合来存储禁止携带的物品列表，这样可以优化检查物品是否在禁止携带列表中的时间复杂度。
   • 使用集合来存储每个学生携带的物品，以优化移除物品的操作。
2. 减少不必要的操作：

• 避免在循环中多次调用 input().split()，可以一次性读取所有输入并存储在列表中。

优化后的代码

# 读取学生数量和禁止携带的物品数量
n, m = map(int, input().split())

# 读取禁止携带的物品列表并转换为集合
forbid_items = set(input().split())

# 初始化违规学生数量和物品数量
out_stu_num = 0
out_item_num = 0

# 读取所有学生的输入并存储在列表中
students = [input().split() for _ in range(n)]

# 处理每个学生的输入
for inputs in students:
    name = inputs[0]
    person_items = set(inputs[2:])  # 将学生携带的物品转换为集合

    # 找出禁止携带的物品
    forbidden_items = person_items & forbid_items

    # 如果有禁止携带的物品
    if forbidden_items:
        print(f"{name}:", end='')
        for item in forbidden_items:
            print(f" {item}", end='')
        print()
        out_stu_num += 1
        out_item_num += len(forbidden_items)

# 输出违规学生的总数和物品总数
print(f"{out_stu_num} {out_item_num}")

代码注释

1. 读取输入：
   • n, m = map(int, input().split())：读取学生数量和禁止携带的物品数量。
   • forbid_items = set(input().split())：读取禁止携带的物品列表并转换为集合。
2. 初始化计数器：
   • out_stu_num = 0 和 out_item_num = 0：初始化违规学生数量和物品数量。
3. 读取所有学生的输入：
   • students = [input().split() for _ in range(n)]：一次性读取所有学生的输入并存储在列表中。
4. 处理每个学生的输入：
   • name = inputs[0]：获取学生姓名。
   • person_items = set(inputs[2:])：将学生携带的物品转换为集合。
   • forbidden_items = person_items & forbid_items：找出禁止携带的物品。
   • 如果有禁止携带的物品，输出学生姓名和禁止携带的物品，并更新违规学生数量和物品数量。
5. 输出结果：

• print(f"{out_stu_num} {out_item_num}")：输出违规学生的总数和物品总数。

时间复杂度和空间复杂度分析

• 时间复杂度：
  • 读取输入的时间复杂度是 O(n + m)。
  • 检查物品的时间复杂度是 O(n * k)，其中 k 是每个学生携带的物品数量的平均值。
  • 使用集合的交集操作 & 的时间复杂度是 O(min(a, b))，其中 a 和 b 分别是两个集合的大小。
• 空间复杂度：

• 存储学生数量 n 和禁止携带的物品数量 m 的空间复杂度是 O(1)。
• 存储禁止携带的物品列表的空间复杂度是 O(m)。
• 存储每个学生携带的物品列表的空间复杂度是 O(n * k)。

通过使用集合，代码在检查物品和移除物品的操作上更加高效，从而优化了时间复杂度和空间复杂度。

---

哲学和编程思想

这些优化方法体现了以下哲学和编程思想：

1. 抽象与封装：

   • 哲学思想：抽象是指从具体事物中提取出共同的、本质的特征，忽略非本质的细节。封装是将数据和操作数据的方法组合在一起，形成一个独立的单元。
   • 编程思想：在代码中，我们将输入处理、数据存储和逻辑处理分别封装在不同的部分，使得代码结构清晰，易于理解和维护。

2. 效率与优化：

   • 哲学思想：效率是指在单位时间内完成的工作量，优化是指通过改进方法或工具来提高效率。
   • 编程思想：我们使用集合（Set）来存储禁止携带的物品列表和学生携带的物品，这样可以利用集合的高效查找特性来优化检查物品是否在禁止携带列表中的时间复杂度。

3. 简洁与清晰：

   • 哲学思想：简洁是指简单明了，不复杂；清晰是指清楚明白，易于理解。
   • 编程思想：代码中避免冗余和复杂的逻辑，使用简洁的语法和结构，使得代码易于阅读和理解。

4. 不变性与可变性：

   • 哲学思想：不变性是指事物保持不变的特性，可变性是指事物可以改变的特性。
   • 编程思想：在代码中，我们使用集合来存储物品，集合是可变的，但我们可以通过集合的交集操作来获取不变的结果，这样可以保持逻辑的稳定性和可预测性。

5. DRY原则（Don't Repeat Yourself）：

   • 哲学思想：DRY原则是指避免重复代码，通过抽象和封装来减少重复。
   • 编程思想：在代码中，我们避免重复读取输入和处理逻辑，通过一次性读取所有输入并存储在列表中，减少了重复操作。

6. KISS原则（Keep It Simple, Stupid）：

   • 哲学思想：KISS原则是指保持简单，避免不必要的复杂性。
   • 编程思想：代码中我们尽量保持简单，避免过度设计，使用简单的数据结构和直接的逻辑处理。

7. YAGNI原则（You Ain't Gonna Need It）：

   • 哲学思想：YAGNI原则是指仅实现当前需要的功能，避免预先设计复杂的功能。
   • 编程思想：在代码中，我们仅实现当前需要的功能，不预先设计复杂的数据结构，而是根据实际需求逐步优化。

8. 单一职责原则（Single Responsibility Principle）：

   • 哲学思想：单一职责原则是指一个模块或类应该只有一个引起它变化的原因。
   • 编程思想：在代码中，每个函数或模块只负责一个功能，例如读取输入、处理逻辑和输出结果，这样可以提高代码的内聚性。

9. 开闭原则（Open/Closed Principle）：

• 哲学思想：开闭原则是指软件实体（类、模块、函数等）应该对扩展开放，对修改关闭。
• 编程思想：在代码中，我们设计可扩展的接口，例如使用集合来存储物品，这样可以方便地在将来需要时添加新功能，而不需要修改现有代码。

通过应用这些哲学和编程思想，代码不仅在性能上得到了优化，而且在结构和设计上更加合理和高效。

---

举一反三

根据上述哲学和编程思想，以及本题目的情况，以下是一些技巧，可以帮助你在编程时举一反三，提高代码的质量和效率：

1. 抽象与封装：
   • 技巧：将复杂的问题分解为更小的、可管理的部分。每个部分负责一个特定的功能，并通过接口进行交互。这样可以使代码更加模块化和易于维护。
   • 应用：在处理复杂的数据结构或算法时，可以创建专门的类或函数来处理特定的任务，而不是将所有逻辑混在一起。
2. 效率与优化：
   • 技巧：选择合适的数据结构和算法来解决问题。了解不同数据结构和算法的性能特点，并根据问题的需求进行选择。
   • 应用：在需要频繁查找或插入操作时，考虑使用哈希表（如Python中的字典）或集合（Set）。在需要排序时，考虑使用快速排序或归并排序。
3. 简洁与清晰：
   • 技巧：编写简洁、清晰的代码。避免不必要的复杂性，使用有意义的变量名和函数名，以及清晰的注释。
   • 应用：在编写代码时，尽量使用Python的内置函数和库，避免自己实现已经存在的功能。
4. 不变性与可变性：
   • 技巧：在设计数据结构时，考虑使用不可变对象（如元组）来避免副作用。在需要修改数据时，考虑使用可变对象（如列表）。
   • 应用：在处理并发或需要保证数据一致性的场景中，使用不可变对象可以减少错误。
5. DRY原则：
   • 技巧：识别和消除重复代码。通过函数或类来封装重复的逻辑，并在需要的地方调用它们。
   • 应用：在多个地方使用相同的逻辑时，创建一个函数或方法来封装这些逻辑，并在需要的地方调用。
6. KISS原则：
   • 技巧：保持代码简单。避免过度设计，仅实现当前需要的功能。
   • 应用：在设计新功能时，先实现最简单的版本，然后根据反馈逐步优化。
7. YAGNI原则：
   • 技巧：仅实现当前需要的功能，避免预先设计复杂的功能。
   • 应用：在项目初期，不要过度设计未来的功能。随着项目的进展，根据实际需求逐步添加功能。
8. 单一职责原则：
   • 技巧：确保每个类或函数只负责一个功能。这样可以提高代码的可读性和可维护性。
   • 应用：在设计类或函数时，确保它们只做一件事，并且做得好。
9. 开闭原则：

• 技巧：设计可扩展的接口，使得在不修改现有代码的情况下可以添加新功能。
• 应用：在设计类或模块时，考虑未来的扩展需求，并设计相应的接口。

通过应用这些技巧，可以在编程时更加灵活和高效，不仅能够解决当前的问题，还能够为未来的需求做好准备。记住，编程是一个不断学习和改进的过程，不断实践这些原则和技巧，编程能力将会不断提高。

---