很多方法需要借助数据结构来操作;
1 数组
2 栈
3 队列
4 堆
5 链表
双端队列(deque,全称为double-ended queue)是一种特殊的线性数据结构,它允许在其两端进行添加和删除操作。在Python中,双端队列由标准库collections模块提供,类名为
collections.deque。相比于列表,双端队列在两端执行插入和删除操作时更加高效,特别是对于大量数据的插入和删除操作,因为deque的底层实现是基于双向链表的,保证了这些操作的时间复杂度为O(1)。双端队列因其高效的插入和删除特性,在多种场景下非常有用:
- 队列和栈: 可以当作先进先出(FIFO)的队列使用(使用
append和popleft),也可以作为后进先出(LIFO)的栈使用(使用append和pop)。- 滑动窗口: 在处理数组或序列问题时,如计算连续子数组的最大和、滑动平均等,deque可以方便地维持一个固定大小的窗口。
- 浏览器导航: 实现浏览器的前进和后退功能,其中前进历史可以用右侧添加,后退历史用左侧添加,通过
popleft和pop来模拟用户操作。- 表达式求值: 解析表达式时,可以使用deque来存储操作符栈。
总之,Python中的
collections.deque是一个灵活且高效的数据结构,特别适合那些需要频繁在两端进行插入和删除操作的应用场景。
https://leetcode.cn/problems/subarray-sum-equals-k/
1 560. 和为 K 的子数组
给你一个整数数组
nums和一个整数k,请你统计并返回 该数组中和为k的子数组的个数 。子数组是数组中元素的连续非空序列。示例 1:
输入:nums = [1,1,1], k = 2 输出:2 示例 2: 输入:nums = [1,2,3], k = 3 输出:2 关键字: 连续子数组的和; 前缀和: 从前面某一个位置数据到当前位置的总和; 一个连续子数组的和 = 两个前缀和的差;
有点动态规划的影子。
1 设定一个字典用:到目前访问a这个下标,之前有多少个这样的前缀子串。
K :V, K 是到目前为止的前缀和, V:有多少个这样的前缀和
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
dict_cum = defaultdict(int)
dict_cum[0] = 1
# 前缀和
cum_nums = 0
res = 0
for i,num in enumerate(nums):
cum_nums += num
# 想一下 dict_cum[cum_nums - k]: 到目前为止的所有前缀和;
res += dict_cum.get(cum_nums-k,0)
dict_cum[cum_nums] = dict_cum.get(cum_nums,0) + 1
return res
2 239. 滑动窗口最大值
给你一个整数数组
nums,有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7示例 2:
输入:nums = [1], k = 1 输出:[1]
2.1 暴力破解
1 遍历数组;
2 固定长度为K窗口,查找最大值;
时间复杂度 O(NK);超时;
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
slid_windows = nums[:k]
max_list = [max(slid_windows)]
for i in range(k,len(nums)):
slid_windows.pop(0)
slid_windows.append(nums[i])
max_list.append(max(slid_windows))
return max_list
2.2 双端队列方法
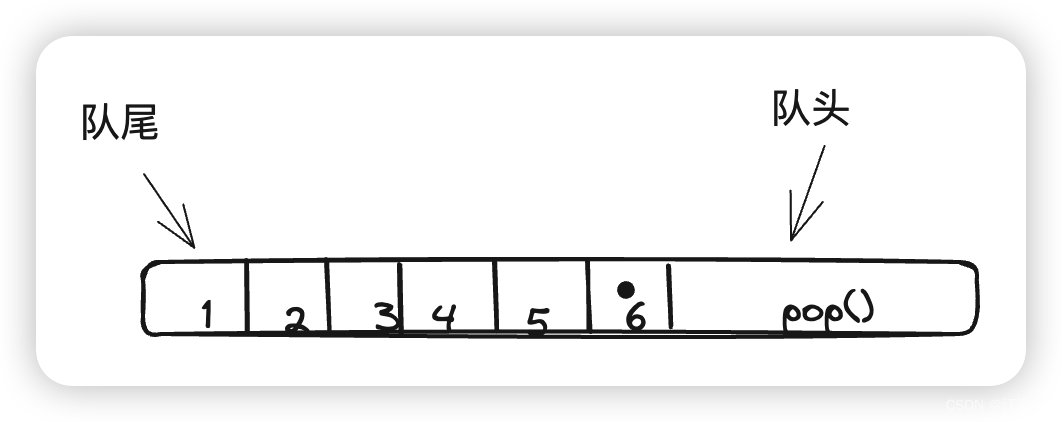
借助一个双端队列:队尾(left)保存之前 (小于)K 个最大值的排序;
队列功能:
1 保存索引;
2 队尾是当前访问的最大值; 这样每一次遍历数组中的元素,把队尾元素拿出来就是最大值了。
3 队是有序的(降序);
如何保证有序?
每次访问一个元素X,就从右到左访问队,如果队头小于X,弹出去;
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
ans = []
q = deque()
for i,x in enumerate(nums):
# 保证降序
while q and nums[q[-1]]<=x:
q.pop()
# 把当前的加入队中
q.append(i)
# 看一下 最大值 是不是已经过界了, 如果最大值在窗口最左边,窗口滑动了,这个元素就要弹出去
if i - q[0] >= k:
q.popleft()
# 保存最大值
if i - k >= -1:
ans.append(nums[q[0]])
return ans
3 76. 最小覆盖子串
给你一个字符串
s、一个字符串t。返回s中涵盖t所有字符的最小子串。如果s中不存在涵盖t所有字符的子串,则返回空字符串""。注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。- 如果
s中存在这样的子串,我们保证它是唯一的答案。示例 1:
输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。示例 2:
输入:s = "a", t = "a" 输出:"a" 解释:整个字符串 s 是最小覆盖子串。
滑动窗口的心法(核心思想)
- 初始化双指针left和right。【初始化】
- 先不断增加right扩大窗口,直到窗口中的内容符合要求。【寻找可行解】
- 停止增加right,不断增加left缩小窗口,直到窗口中的内容不再满足要求。在每次增加left时都要更新所求的结果。【优化可行解】
- 不断重复扩大窗口、缩小窗口的操作,直到right到达序列的末端。
def slidingWindow(s:str,t:str): '''初始化 window 和 need 两个哈希表,记录窗口中的字符和需要凑齐的字符:''' need, window = collections.defaultdict(int), collections.defaultdict(int) # {char:int} for c in t: need[c] += 1 left, right = 0, 0 valid = 0 # 表示窗口中满足need条件的字符个数,如果valid和len(need)的大小相同,则说明窗口已满足条件 '''使用 left 和 right 变量初始化窗口的两端,不要忘了,区间 [left, right) 是左闭右开的,所以初始情况下窗口没有包含任何元素:''' while right < len(s): # c是将要移入窗口的字符 c = s[right] # 增大窗口 right += 1 # 进行窗口内数据的一系列更新 ..."""更新窗口数据的地方""" # 判断左侧窗口是否要收缩 while '''window needs shrink''': # d是将要移出窗口的字符 d = s[left] # 缩小窗口 left += 1 # 进行窗口内数据的一系列更新 ..."""更新窗口数据的地方"""
class Solution:
def minWindow(self, s: str, t: str) -> str:
patt_set = defaultdict(int)
current_set = defaultdict(int)
for c in t:
patt_set[c]+=1
need = 0
# 最小开始, 长度
start ,length = 0, sys.maxsize
right ,left = 0, 0
while right < len(s):
c = s[right]
right += 1
if c in patt_set:
current_set[c] += 1
if current_set[c]==patt_set[c]:
need+=1
# 查看是否满足条件,然后让窗口不满足条件
while need == len(patt_set):
if right - left < length:
start = left
length = right - left
# 缩小窗口
c = s[left]
#print(left,c, len(s), patt_set, current_set)
left += 1
if c in current_set:
if current_set[c] == patt_set[c]:
need -= 1
current_set[c] -= 1
return "" if length==sys.maxsize else s[start: start+length]