简单的介绍一下用堆排序的算法对整形数据的数据进行排序。
一、堆的概念
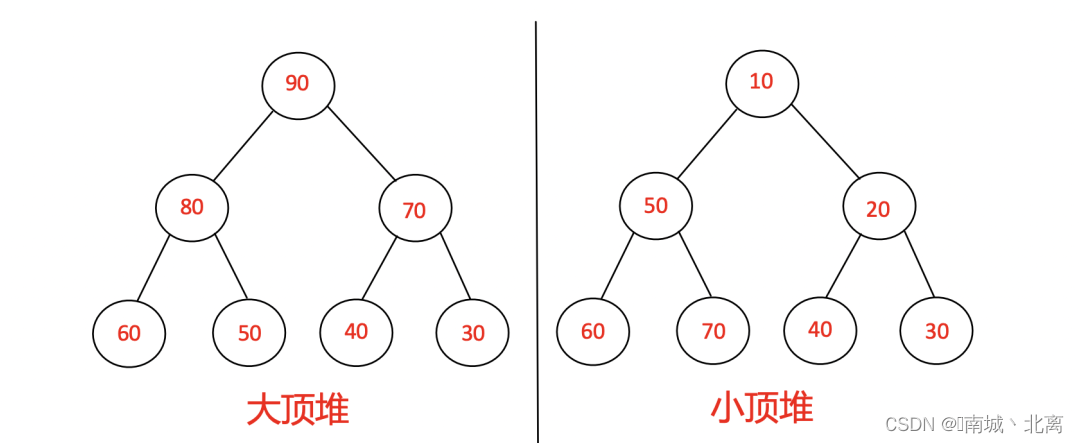
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子节点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
大顶堆和小顶堆的示意图:
二、堆排序的算法
因为数组具有顺序结构,而我们的完全二叉树可以使用顺序结构来表示,所以我们可以用堆对数组进行排序。
(一)、算法思路
这里介绍一下排升序的方法,等明白了思路后,排降序自然也会了。
假设数组的元素个数为n,将待排序的数组构造成一个大顶堆。此时,整个数组的最大值就是堆顶的根节点。将它移走(将其与堆数组的末尾元素进行交换,此时末尾元素就是最大值),这样我们待排序的数组的最大值就排到了正确的位置上。然后我们把剩余的n-1个元素重新构成一个大顶堆,这样堆顶元素就是我们的次大值,将其移走,次大值的元素也就排好了。如此反复执行,就得到了一个升序的数组。如果我们要排降序的数组,则需要建小顶堆。
于是我们就有了两个问题。一是:如何把一个无序的数组构建成大顶堆?在将堆顶元素移走后要怎么将剩余的数组元素重新调整为堆?
(二)、向上调整和向下调整
向上调整针对的是当将一个新的元素插入到一个堆中时,将新插入的元素向上进行调整,将其二叉树保持原来的堆的结构。如果是使用堆来对一个数组进行排序的话,使用向下调整就足够了,所以我们先讲向下调整,当我们实现了对数组的堆排序后,再回来看向上调整。
1、向下调整
向下调整的作用就是,当我们在一个堆的结构中,把堆顶元素给替换成别的值后,其堆顶处极可能已经不满足大顶堆和小顶堆的要求了,这个时候我们就需要把这个堆顶位置的元素向下调整到合适的位置,使其重新满足堆的要求。
例如下面这个例子:
这是一个大顶堆,当我们用20替换其堆顶元素时,其不再满足大顶堆的结构,这时我们需要对堆顶的20进行向下调整。具体方法如如下:
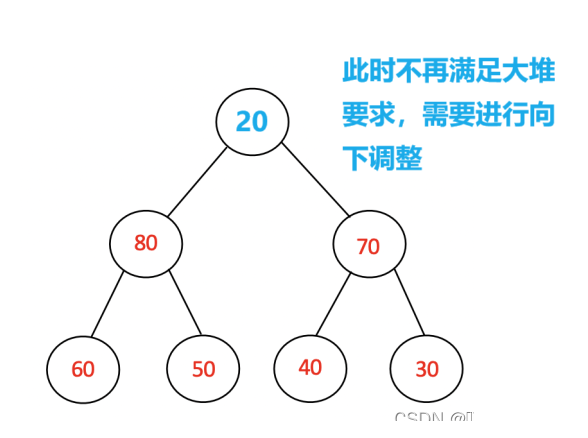
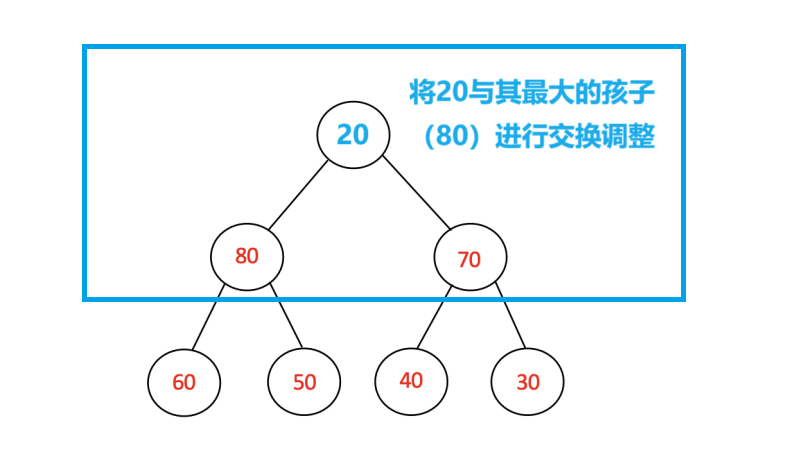
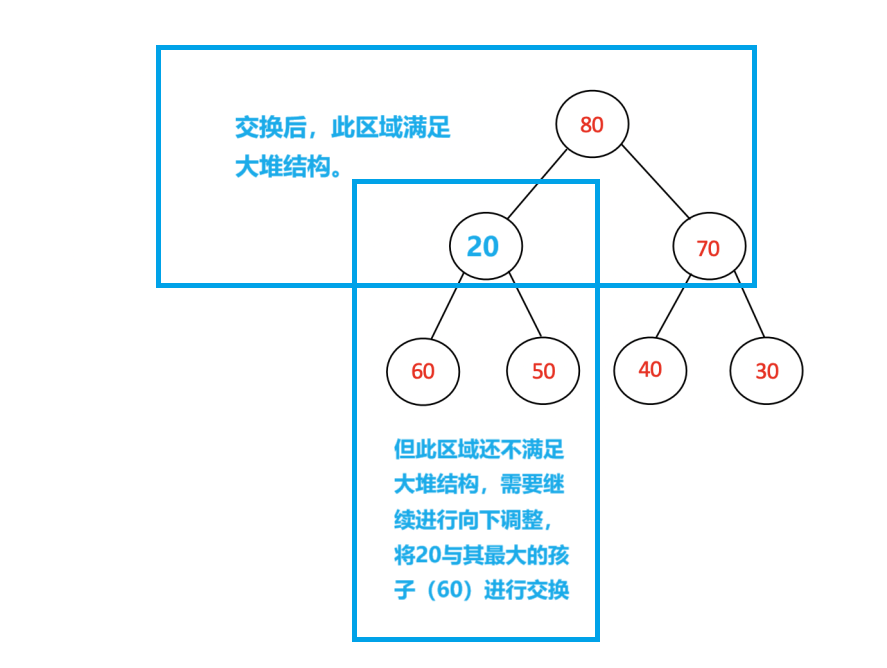
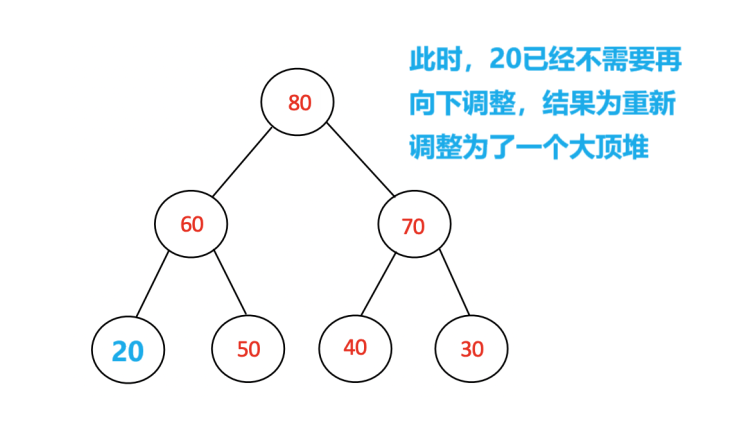
具体代码:
//向下调整为大顶堆
void AdjustDown(int* arr,int left,int right)//传入数组和要向下调整的区间
{
int pos = left;//记录向下调整的位置
int temp = arr[pos];//保存向下调整的值
for (int i = left * 2; i <= right; i *= 2)//遍历其要向下调整的结点的孩子
{
//找到其左孩子和右孩子的最大值 如果右孩子不存在,则最大值就算为左孩子
if (i + 1 <= right && arr[i] < arr[i + 1])
i++;//此时i指向右孩子
if (temp < arr[i]) //如果要向下调整的值不如孩子大
arr[pos] = arr[i];
else
break;
//更新要向下调整的值的下标位置
pos = i;
}
//向下调整完毕,此时pos的位置就是要向下调整的值的最终位置
arr[pos] = temp;
}2、向上调整
向上调整非常简单,只需要将插入的值的结点与其双亲结点相比较,如果比双亲大,那么就交换位置,一直重复该过程。




//向上调整为大堆顶
void AdjustUp(int* arr,int index)
{
int pos = index;//记录向上调整的值的位置
int temp = arr[index];//保存向上调整的值
//遍历其双亲节点进行向上调整,如果向上调整的下标为0或比双亲小就结束
for (int i = pos / 2; pos > 0; i /= 2)
{
if (temp > arr[i])
arr[pos] = arr[i];
else
break;
//更新pos的位置
pos = i;
}
//向上调整完毕,此时pos位置就是向上调整的值的位置
arr[pos] = temp;
}(三)、将无序数组转化为大顶堆
实现方法:从最后一个叶子结点(就是数组的最后一个元素的下标的位置的结点)处的双亲结点开始,对该结点以及该结点之前的所有结点进行向下调整操作,这样就可以把无序数组转化为了大顶堆的结构。下面是将一个无序数组转化为大顶堆的示意图(标识为蓝色的值就是需要依次进行向下调整的结点。)
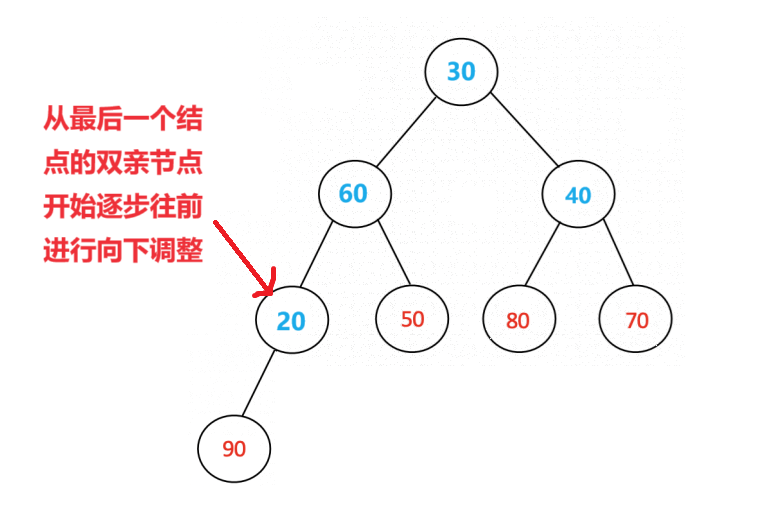
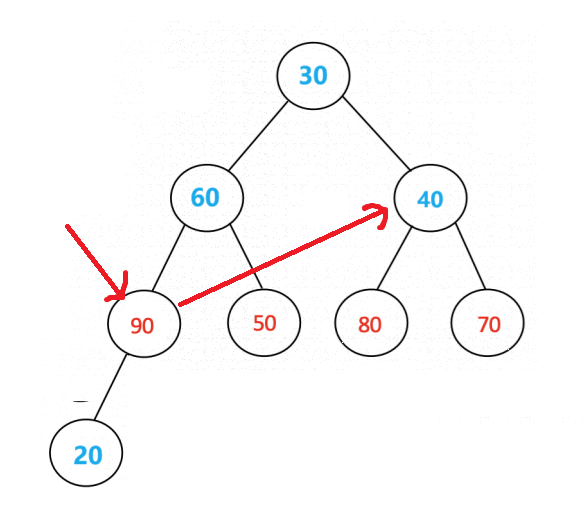
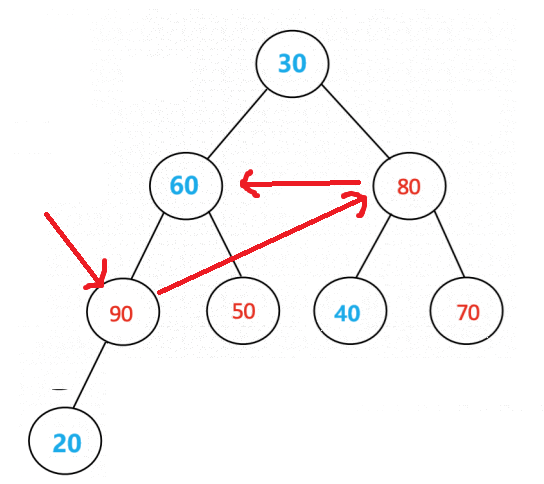

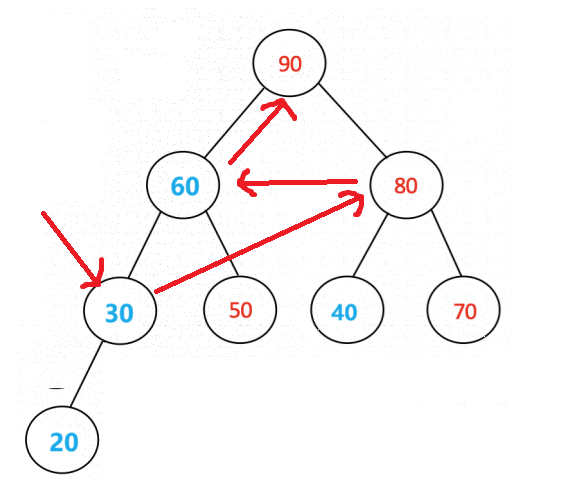
就这样,我们就将一个无序的数组转化为了一个具有大顶堆结构的数组了。
我们也可以从0开始遍历数组,每次执行一次向上调整,这样也可以建堆,但是其消耗比较大。因为需要对每个结点进行向上调整操作,而我们的向下调整建堆是不需要对最后一层的结点进行向下调整的,在一棵满二叉树中,最后一层的结点数就占了整棵树一半的结点数,这意味着向上调整建堆比向下调整建堆多用了很多时间。
(四)、堆排序的最终实现
我们以一个大顶堆为例,看看将大顶堆转化成一个升序的数组的过程。
来看下面这个大顶堆,是如何变升序的。
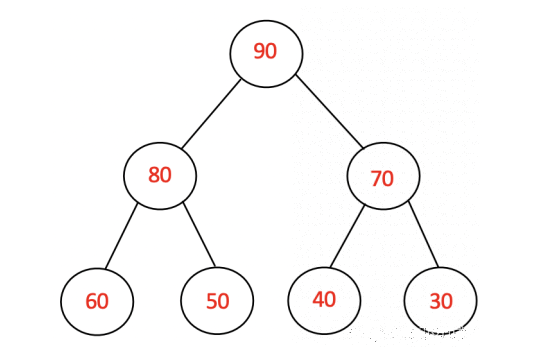


此时90排好了。



此时80就排好了。

如此往复......

具体代码:
//堆排序
void HeapSort(int* arr, int nums)
{
//先从最后一个节点的双亲结点注逐一往前进行向下调整,将数组调整为大堆
for (int i = (nums - 1) / 2; i >= 0; i--)
{
AdjustDown(arr,i, nums - 1);
}
//将最大值放置到末尾然后将其与堆的联系解除,然后再对堆顶元素向下调整
for (int i = nums - 1; i >= 1; i--)
{
swap(arr[0], arr[i]);
AdjustDown(arr, 0, i - 1);
}
}三、堆排序的时间复杂度
堆排序不需要额外开辟空间,所以空间复杂度为O(1)。
时间消耗上主要在初始建堆和在反复重建堆的时间上。而我们对无序数组进行建堆所需要的时间复杂度为O(n),而我们在排序时,每次都需要对堆顶进行向下排序,其时间复杂度为O(nlogn)。所以堆排序的时间复杂度为O(nlogn)。