链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
题目描述
给一个 n×mn\times mn×m 矩阵迷宫, 第 iii 行第 jjj 列的值为 ci,jc_{i,j}ci,j ,LHLHLH 在迷宫中迷路了,他需要你的帮助。
LHLHLH 当前在 (1,1)(1,1)(1,1) 的位置,出口在 (n,m)(n,m)(n,m),这个迷宫有一个计数器,只有当计数器的值模 (p−1)(p-1)(p−1) 的余数为 000 时迷宫出口才会开门(出口没有开门意味着即使在 (n,m)(n,m)(n,m) 的位置也不能逃出去)。
LHLHLH 每一秒会向迷宫的上下左右四个方向走一步(不可以不走),并且不能走出迷宫的边界,假设 LHLHLH 从 (i,j)(i,j)(i,j) 走到了 (i′,j′)(i',j')(i′,j′),然后计数器将会加上 ci′,j′c_{i',j'}ci′,j′。
特别的,计数器初始是 c1,1c_{1,1}c1,1。
ci,j=ai,j×p2bi,jc_{i,j}=a_{i,j}\times p^{2^{b_{i,j}}}ci,j=ai,j×p2bi,j。
现在 LHLHLH 问你,他最快需要多久才可以走出迷宫。
输入描述:
第一行输出三个整数 n,m,p(1≤n,m≤10,2≤p≤104)n,m,p(1\le n,m\le 10,2\le p\le 10^4)n,m,p(1≤n,m≤10,2≤p≤104)。
接下来输入一个 nnn 行 mmm 列的矩阵 ai,ja_{i,j}ai,j。
接下来输入一个 nnn 行 mmm 列的矩阵 bi,jb_{i,j}bi,j。
0≤ai,bi≤1060\le a_i,b_i\le 10^60≤ai,bi≤106。
输出描述:
输出一个整数,表示满足条件的最短路径长度。 假如不存在一条路径满足条件,输出 −1-1−1。
示例1
输入
复制3 3 10 1 2 3 0 1 4 0 0 0 1 0 0 0 0 1 0 1 0
3 3 10 1 2 3 0 1 4 0 0 0 1 0 0 0 0 1 0 1 0
输出
复制6
6
备注:
C=[1002030010400000]C=\begin{bmatrix}
100 &20 &30 \\
0& 10 & 400\\
0& 0 &0
\end{bmatrix}C=⎣⎡1000020100304000⎦⎤。
第一秒,从 (1,1)(1,1)(1,1) 走到 (1,2)(1,2)(1,2),计数器的值为 120120120。
第二秒,从 (1,2)(1,2)(1,2) 走到 (1,3)(1,3)(1,3),计数器的值为 150150150。
第三秒,从 (1,3)(1,3)(1,3) 走到 (1,2)(1,2)(1,2),计数器的值为 170170170。
第四秒,从 (1,2)(1,2)(1,2) 走到 (2,2)(2,2)(2,2),计数器的值为 180180180。
第五秒,从 (2,2)(2,2)(2,2) 走到 (3,2)(3,2)(3,2),计数器的值为 180180180。
第六秒,从 (3,2)(3,2)(3,2) 走到 (3,3)(3,3)(3,3),计数器的值为 180180180,是 999 的倍数,逃出迷宫。
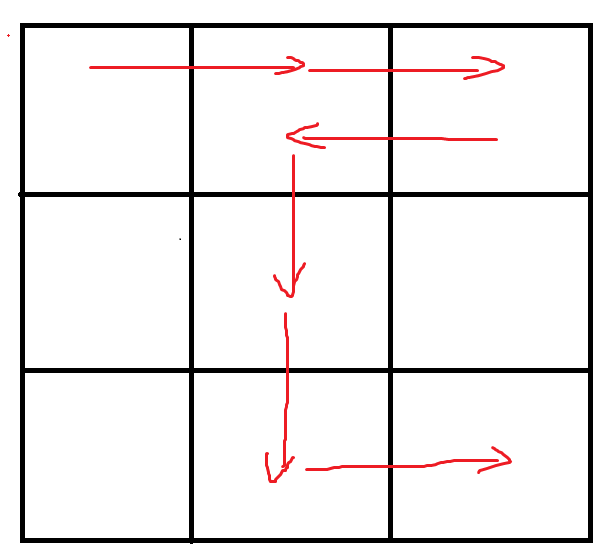
做法
bfs+dp。赛时想不到怎么弄,因为它可以走重复的格子,vis[i][j]不能用了限制循环次数。也没想到Cij的值直接可以化为Aij。我们可以加多一维来表示余数,即dp[i][j][k]表示走到第i行j列且余数为k的最短路。用vis[i][j][k]来限制循环次数,因为之前已经求出最短路了,再次经过该点不可能比之前再短了,所以直接跳过。
代码
#include<bits/stdc++.h>
using namespace std;
int n,m,p;
int a[20][20],b[20][20];
int dp[20][20][10010];
int vis[20][20][10010];
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
struct ty{
int x,y,res;
};
queue<ty> q;
void bfs(){
memset(dp,sizeof(dp),0x3f);
q.push({1,1,a[1][1]%p});
vis[1][1][a[1][1]%p]=1;
dp[1][1][a[1][1]%p]=0;
while(!q.empty()){
ty tmp=q.front();
q.pop();
for(int i=0;i<4;i++){
int x=tmp.x+dx[i];
int y=tmp.y+dy[i];
if(x>n||x<=0||y>m||y<=0) continue;
if(vis[x][y][(tmp.res+a[x][y])%p]) continue;
dp[x][y][(tmp.res+a[x][y])%p]=dp[tmp.x][tmp.y][tmp.res]+1;
vis[x][y][(tmp.res+a[x][y])%p]=1;
q.push({x,y,(tmp.res+a[x][y])%p});
}
}
if(dp[n][m][0]!=0x3f3f3f3f) cout<<dp[n][m][0];
else cout<<-1;
}
int main(){
cin>>n>>m;
scanf("%d",&p);
p--;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&b[i][j]);
}
}
bfs();
}