文章目录
- 相邻两个有序子序列的归并
- 归并排序算法
- 归并排序算法分析
基本思想
- 将两个或两个以上的有序子序列归并为一个有序序列。
- 在内部排序中,通常采用的是2-路归并排序。
- 即:将两个位置相邻的有序子序列 R[l…m] 和 R[m+1…n] 归并为一个有序序列 R[l…n]。
举个例子
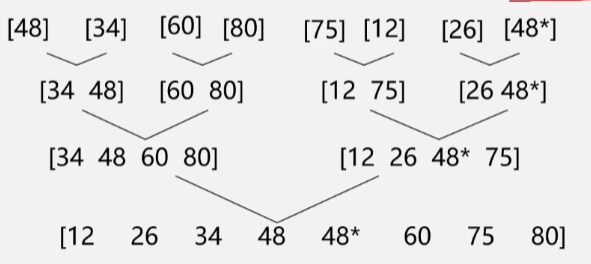
- 假设初始关键字序列为:{48,34,60,80,75,12,26,48*}。
- 初始序列有 n 个记录,则可看成是 n 个有序的子序列,每个子序列的长度为 1,然后两两归并,得到 n/2 个长度为 2 或 1 的有序子序列;
- 再两两归并,……如此重复,直到得到一个长度为 n 的有序序列位置。
- 归并排序完成之后的图形很像一棵倒着的树,所以将这种树称为归并树。
- 归并排序需要的趟数就是树的高度,树的高度则是 nlog₂n,也就是说整个归并排序仅需要 nlog₂n 趟。
相邻两个有序子序列的归并
算法步骤
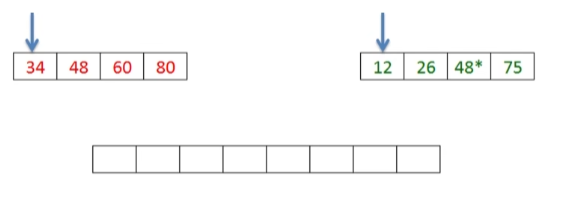
- 假设两个有序表存放在同一数组中相邻的位置上:R[low…mid] 和 R[mid+1…high],每次分别从两个表中取出一个记录进行关键字的比较,将较小者放入 T[low…high] 中,重复此过程,直到其中一个表为空,最后将另一个非空表余下的部分直接复制到 T 中。
举个例子
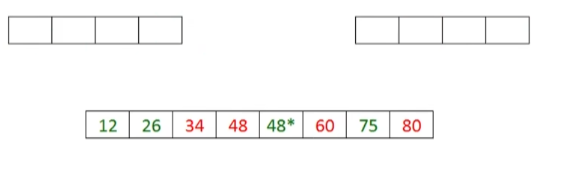
- 用两个指针分别代表元素的下标,
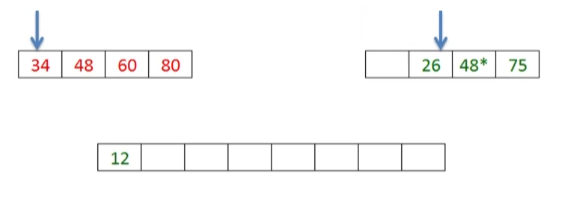
- 比较一下当前两个子序列的第一个元素,谁小就将谁放到新的数组当中。
- 将值存进新数组以后,将指向被拿出元素的数组下标的指针往后移。
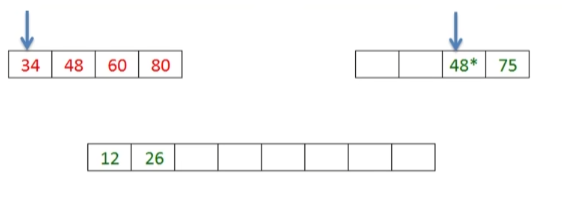
- 再比较两个指针指向的元素,小的存进新数组,然后将指针后移。
- 重复上述步骤,直到其中一个子序列为空为止,最后将另一个非空表中剩下的元素直接搬到新数组中。
算法描述
//将有序表R[low...mid]和R[mid+1...high]归并为有序表T[low...high]
void Merge(RedType R[],RedType T[],int low,int mid,int high)
{
int i = low;
int j = mid + 1;
int k = low;
while(i <= mid && j <= high)//将R中记录由小到大并入T中
{
if(R[i].key <= R[j].key)
{
T[k++] = R[i++];
}
else
{
T[K++] = R[j++];
}
}
while(i <= mid)//将剩余的R[i...mid]的元素复制到T中
{
T[k++] = R[i++];
}
while(j <= high)//将剩余的R[j...high]的元素复制到T中
{
T[k++] = R[[j++];
}
}
归并排序算法
算法步骤
2-路归并排序将 R[low…high] 中的记录归并排序后放入 T[low…high] 中。当序列长度等于1时,归并结束,否则:
- 将当前序列一分为二,求出分裂点 mid = (low +high) / 2;
- 对左子序列 R[low…mid] 递归,进行归并排序,将结果放入新数组 S[low…mid] 中;
- 对右子序列 R[mid + 1…high] 递归,进行归并排序,结果放入新数组 S[mid + 1…high]中;
- 调用函数 Merge,将有序的两个子序列 S[low…mid] 和 S[mid +1…high] 归并为一个有序的序列 T[low…high]。
算法描述
//将R[low...ghig]归并排序后放入T[low...high]中
void MSort(RedType R[],RedType T[],int low,int high)
{
if(low == high)
{
T[low] = R[low];
}
else
{
mid = (low + high) / 2;//将当前序列一分为二,求出分裂点 mid
MSort(R,S,low,mid);//对子序列R[low...mid]递归归并排序,将结果放入S[low...mid]中
MSort(R,s,mid+1,high);//对子序列R[mid...highg]递归归并排序,将结果放入S[mid+1...high]中
Merge(S,T,low,mid,high);//将S[low...mid]和S[mid+1...high]归并到T[low...high]
}
}
//对顺序表L做归并排序
void MergeSort(SqList &L)
{
MSort(L.r,L.r,1,L.length);
}
归并排序算法分析
- 时间效率:O(nlog₂n)
- 当有 n 个记录时,需要进行 log₂n 趟归并排序,每一趟归并,其关键字比较次数不超过 n,元素移动次数都是 n,因此,归并排序的时间复杂度为 O(nlog₂n)。
- 空间效率:O(n)。
- 因为需要一个与原始序列同样大小的辅助序列(R1)。这正是此算法的缺点。
- 稳定性:稳定。