嵌入式学习——数据结构（队列、二叉树）——day49

news2024/11/24 20:20:00

1. 队列

1.1 定义

        是一种线性数据结构类型，可以用数组或链表等基础数据结构来实现。它遵循先进先出（FIFO，First In First Out）的原则。这意味着最先进入队列的元素会最先被移出。

1.2 基本概念

  • 队列（Queue）: 一种线性数据结构，遵循先进先出原则。
  • 元素（Element）: 队列中的单个数据项。
  • 头（Front）: 队列中最早添加的元素的位置，出队（dequeue）操作在此位置进行。
  • 尾（Rear）: 队列中最后添加的元素的位置，入队（enqueue）操作在此位置进行。

1.3 基本操作

  • 入队（Enqueue）: 将元素添加到队列的尾部。
  • 出队（Dequeue）: 移除并返回队列头部的元素。
  • 检查队首元素（Peek/Front）: 返回队列头部的元素，但不移除。
  • 检查队列是否为空（IsEmpty）: 判断队列是否为空。
  • 检查队列是否已满（IsFull）（在固定大小的队列中）: 判断队列是否已满。

1.4 实现方法

  • 数组实现: 使用固定大小的数组实现队列，需处理数组的循环利用（环形队列）。
  • 链表实现: 使用链表（单链表或双链表）实现队列，动态分配内存，无需预先指定大小。

1.5 应用场景

  • 操作系统中的任务调度: 进程调度、打印任务管理。
  • 广度优先搜索（BFS）: 用于图和树的遍历。
  • 缓冲区（Buffer）: 数据流的处理，网络数据包的传输。
  • 模拟现实世界的排队场景: 银行队列、超市结账等。

2. 链式队列——（一个指针指向头、一个指针指向尾）

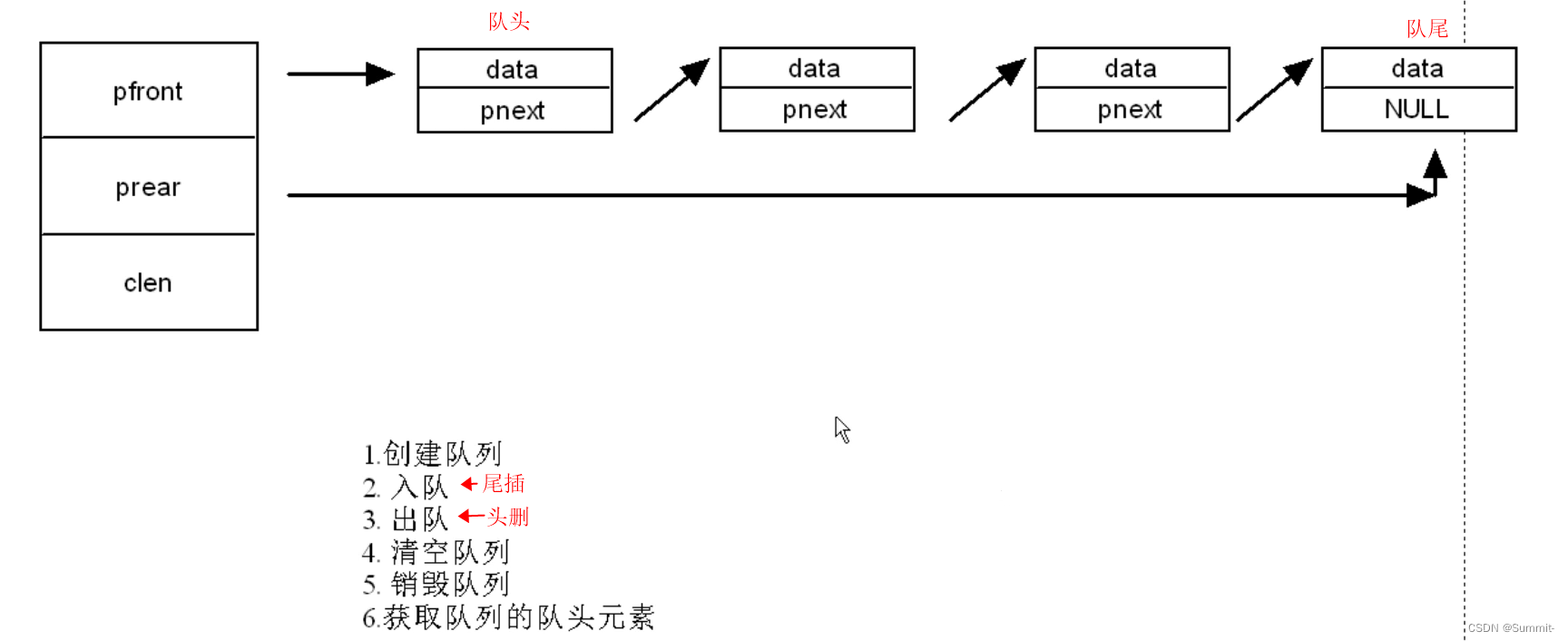
2.1 makefile

OBJ:=a.out
OBJS+=main.c queue.c
CCl=gcc

$(OBJ):$(OBJS)
	$(CC) $^ -o $@
.PHONY:
clean:
	rm $(OBJ)
test:
	valgrind --tool=memcheck --leak-check=full ./$(OBJ)

2.2 queue.h

#ifndef __QUEUE_H__
#define __QUEUE_H__


typedef int DataType;

typedef struct que_node
{
	DataType data;
	struct que_node *pnext;
}QueNode;

typedef struct que_list
{
	QueNode *pfront;//指向队首
	QueNode *prear;//指向队尾
	int clen;
}QueList;

extern QueList *create_queue();
extern int push_queue(QueList *, DataType );
extern int pop_queue(QueList *, DataType *);
extern void queue_for_each(QueList *pque);
extern int get_queue_front(QueList *, DataType *);
extern void destroy_queue(QueList *);
extern void clear_queue(QueList *);
extern int is_empty_queue(QueList *pque);

#endif

2.3 queue.c

#include "queue.h"
#include <stdlib.h>
#include <stdio.h>

QueList *create_queue()
{
	QueList *pque = malloc(sizeof(QueList));
	if (NULL == pque)
	{
		perror("fail malloc");
		return NULL;
	}
	pque->pfront = NULL;
	pque->prear = NULL;
	pque->clen = 0;

	return pque;
}

int is_empty_queue(QueList *pque)
{
	if (NULL == pque->pfront)
	{
		return 1;
	}
	return 0;
}

int push_queue(QueList *pque, DataType data)//入队——尾插
{
	QueNode *pnode = malloc(sizeof(QueNode));
	if (NULL == pnode)
	{
		perror("fail malloc");
		return -1;
	}
	pnode->data = data;
	pnode->pnext = NULL;
	
	if (is_empty_queue(pque))//空队列
	{
		pque->pfront = pnode;
		pque->prear = pnode;
	}
	else
	{
		pque->prear->pnext = pnode;
		pque->prear = pnode;
	}
	pque->clen++;

	return 0;
}

int pop_queue(QueList *pque, DataType *pdata)//出队——头删
{
	if (is_empty_queue(pque))
	{
		return 1;
	}
	
	QueNode *pfree = pque->pfront;
	pque->pfront = pfree->pnext;//prear没动，只用修改front的指向

	if (pdata != NULL)//如果传入数据指针非空，把将要删除的数据传出函数
	{
		*pdata = pfree->data;
	}

	free(pfree);
	pque->clen--;

	if (NULL == pque->pfront)//如果队列删为空，将指向队尾的指针置为空，不为空，尾指针不变
	{
		pque->prear = NULL;
	}

	return 0;
}

void queue_for_each(QueList *pque)
{
    QueNode *pnode = pque->pfront;

    while (pnode != NULL)
    {
        printf("%d ", pnode->data);
        pnode = pnode->pnext;
    }
    putchar('\n');
}

int get_queue_front(QueList *pque, DataType *pdata)//获得头指针数据
{
	if (is_empty_queue(pque))
	{
		return -1;
	}
	*pdata = pque->pfront->data;

	return 0;
}

void clear_queue(QueList *pque)//清空队列
{
	while (!is_empty_queue(pque))
	{
		pop_queue(pque, NULL);
	}
}

void destroy_queue(QueList *pque)//摧毁队列
{
	clear_queue(pque);
	free(pque);
}

2.4 main.c

#include <stdio.h>
#include "queue.h"


int main(int argc, const char *argv[])
{
    int i = 0;
    int ret = 0;
	DataType push_data[] = {1, 2, 3 ,4, 5};
	DataType data;//取出的队头元素
	QueList *pque = create_queue();	
	if (NULL == pque)
	{
		return -1;
	}
	
    for (i = 0; i < sizeof(push_data)/sizeof(push_data[0]); i++)//入队
    {
	    push_queue(pque, push_data[i]);
        queue_for_each(pque);
    }

#if 0
    for (i = 0; i < sizeof(push_data)/sizeof(push_data[0]); i++)//出队
    {
        queue_for_each(pque);
	    pop_queue(pque, NULL);
    }
#endif

#if 1
	ret = get_queue_front(pque, &data);//获得队头元素
	if (0 == ret)
	{
		printf("front data = %d\n", data);
	}

	destroy_queue(pque);
#endif

	return 0;
}

3. 队列和栈结构的区别

3.1 数据结构特性

  • 栈：栈是一种后进先出（LIFO，Last In First Out）的数据结构，最后压入栈的元素最先弹出。
  • 队列：队列是一种先进先出（FIFO，First In First Out）的数据结构，最先进入队列的元素最先被移出。

3.2 操作

  • 栈：栈支持的主要操作是压入（push）和弹出（pop）。元素只能从栈顶进行操作，不支持在中间插入或者访问非栈顶元素。
  • 队列：队列支持的主要操作是入队（enqueue）和出队（dequeue）。元素只能从队列的头部删除（出队），从尾部添加（入队）。

3.3 访问元素方式

  • 栈：只能访问栈顶元素，即最后压入栈的元素。
  • 队列：可以访问队首和队尾的元素，但出队操作通常只能操作队首元素。

3.4 应用场景

  • 栈：适合于需要后进先出访问顺序的场景，例如表达式求值、逆序输出、深度优先搜索的非递归实现等。
  • 队列：适合于需要先进先出访问顺序的场景，例如广度优先搜索、缓冲区管理、任务调度等。

4. 树型结构——（一对多的非线性结构，由节点和边组成，具有层次的特点）

4.1 基本概念

  • 节点（Node）：树中的基本元素，每个节点包含一个数据元素及其子节点。
  • 边（Edge）：连接两个节点的路径。
  • 根节点（Root）：树的起始节点，没有父节点。
  • 子节点（Child）：某个节点的直接下属节点。
  • 父节点（Parent）：某个节点的直接上级节点。
  • 叶节点（Leaf）：没有子节点的节点。
  • 内部节点（Internal Node）：至少有一个子节点的节点。
  • 子树（Subtree）：节点及其所有后代节点构成的树。
  • 深度（Depth）：从根节点到某个节点的边数。
  • 高度（Height）：从某个节点到叶节点的最长路径的边数。
  • 度（Degree）：一个节点的子节点数量。
  • 路径（Path）：从一个节点到另一个节点经过的节点序列。
  • 叶子节点（终端节点）：只有前驱节点没有后继节点
  • 非叶子节点（分支节点）：根节点和叶子节点之间的节点
  • 结点度：某节点后继节点的个数称
  • 树的（广）度：树中各节点度的最大值 （整个树中某个节点的后继节点的最大值）
  • 深度：从根节点到最底层节点的层数

4.2 树的分类

（1）二叉树（Binary Tree）：每个节点最多有两个子节点（左子节点和右子节点）。

  • 满二叉树（Full Binary Tree）：所有节点要么是叶节点，要么有两个子节点。
  • 完全二叉树（Complete Binary Tree）：除了最后一层，其他层的节点都是满的，最后一层的节点从左到右连续排列。
  • 平衡二叉树（Balanced Binary Tree）：任何节点的两个子树的高度差至多为1。
  • 搜索二叉树（Binary Search Tree，BST）：左子节点的值小于父节点，右子节点的值大于父节点。

注意：1. 满二叉树第K层有2^(k-1)个节点
               K层满二叉树总共有2^k-1个节点

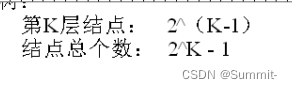
           2. 完全二叉树

                在满二叉树的基础上
                1. 增加节点：从左到又，从上到下依次增加
                2. 减少节点：从下往上，从右往左依次减少

          3. 满二叉树一定是完全二叉树

              完全二叉树不一定是满二叉树

          4. 已知完全二叉树的总节点个数，计算完全二叉树的叶子节点个数

                解：通过注意1中满二叉树的规律，利用节点总个数和倒数第二层和倒数第一层的节点个数得出结果

（2）树堆（Heap）

  • 最大堆（Max Heap）：每个节点的值都大于等于其子节点的值。
  • 最小堆（Min Heap）：每个节点的值都小于等于其子节点的值。

（3）多路树（M-ary Tree）：每个节点最多有 M 个子节点。

  • B树（B-Tree）：一种自平衡的多路查找树，用于数据库和文件系统。
  • B+树（B+ Tree）：B树的变种，所有值都在叶子节点，内部节点只存储索引。

（4）其他特殊树：

  • 前序遍历（Pre-order Traversal）：根节点 -> 左子树 -> 右子树
  • 中序遍历（In-order Traversal）：左子树 -> 根节点 -> 右子树
  • 后序遍历（Post-order Traversal）：左子树 -> 右子树 -> 根节点
  • 层序遍历（Level-order Traversal）：按层次从上到下、从左到右访问节点

4.3 树的应用场景

  • 搜索和排序：二叉搜索树、AVL树、红黑树等用于快速搜索、插入和删除操作。
  • 优先队列：堆用于实现优先队列，广泛应用于任务调度、图算法中的最短路径等。
  • 数据库和文件系统：B树和B+树用于实现高效的数据库索引和文件系统管理。
  • 字符串处理：字典树用于高效的前缀匹配和单词检索。

5. 二叉树的遍历

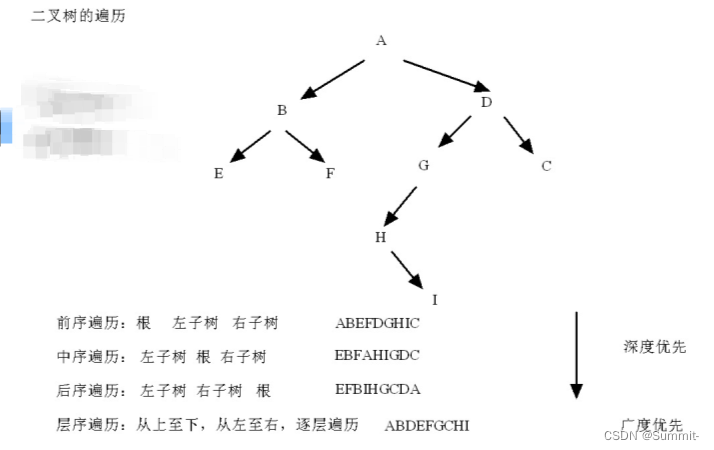
5.1 前序遍历 根 左 右

5.2 中序遍历 左 根 右

5.3 后序遍历 左 根 右

        注意：前、中、后序遍历又叫深度优先

5.4 层序遍历 从上到下、从左至右，逐层向下遍历

        注意：层序遍历又叫广度优先

5.5 二叉树的遍历特性

        已知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树；
        已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树；

6. 二叉树实现代码——以递归为主

6.1 makefile

OBJ:=a.out
OBJS+=main.c tree.c queue.c
CCl=gcc

$(OBJ):$(OBJS)
	$(CC) $^ -o $@
.PHONY:
clean:
	rm $(OBJ)
test:
	valgrind --tool=memcheck --leak-check=full ./$(OBJ)

6.2 tree.h

#ifndef __TREE_H__
#define __TREE_H__

typedef char TreeDataType;

typedef struct node
{
	TreeDataType data;
	struct node *pl;
	struct node *pr;
}TreeNode;

extern TreeNode *create_bin_tree();
extern void pre_order(TreeNode *proot);
extern void mid_order(TreeNode *proot);
extern void pos_order(TreeNode *proot);
extern int get_tree_node_cnt(TreeNode *proot);
extern int get_tree_layer_cnt(TreeNode *proot);
extern void destroy_tree(TreeNode *proot);
extern void layer_order(TreeNode *proot);
	
#endif

6.3 tree.c

#include "tree.h"
#include <stdio.h>
#include <stdlib.h>
#include "queue.h"

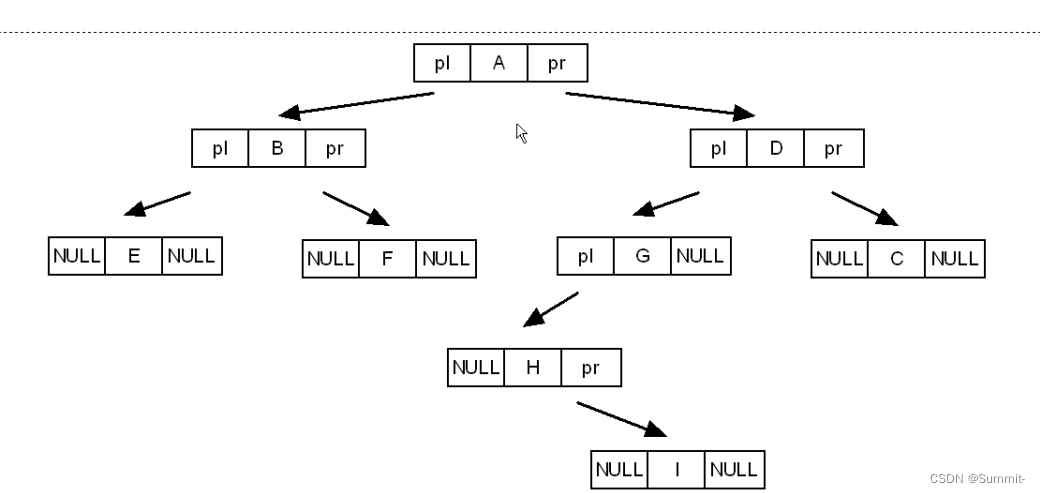
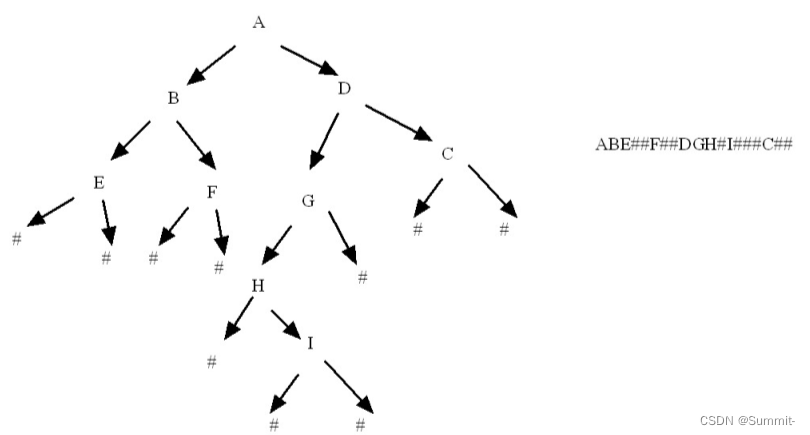
char tree[] = {"ABE##F##DGH#I###C##"};
int idx = 0;

TreeNode *create_bin_tree()//二叉树的创建
{
	TreeDataType data = tree[idx++];//tree数组后移的方式
	if ('#' == data)//一个叶子节点遍历结束的标志
	{
		return NULL;
	}

	TreeNode *pnode = malloc(sizeof(TreeNode));
	if (NULL == pnode)
	{
		perror("fail malloc");
		return NULL;
	}
	pnode->data = data;
	pnode->pl = create_bin_tree();//创建总子树
	pnode->pr = create_bin_tree();//创建右子树
	
	return pnode;
}

void pre_order(TreeNode *proot)//前序遍历 根 左 右
{
	if (NULL == proot)//一次前序遍历结束的标志
	{
		return ;
	}

	printf("%c", proot->data);
	pre_order(proot->pl);
	pre_order(proot->pr);
}

void mid_order(TreeNode *proot)//中序遍历 左 根 右
{
	if (NULL == proot)
	{
		return ;
	}

	mid_order(proot->pl);
	printf("%c", proot->data);
	mid_order(proot->pr);
}

void pos_order(TreeNode *proot)//后续遍历 左 右 根
{
	if (NULL == proot)
	{
		return ;
	}

	pos_order(proot->pl);
	pos_order(proot->pr);
	printf("%c", proot->data);
}

int get_tree_node_cnt(TreeNode *proot)//获取二叉树节点个数
{
	if (NULL == proot)
	{
		return 0;
	}

	return 1+get_tree_node_cnt(proot->pl)+get_tree_node_cnt(proot->pr);
}

int get_tree_layer_cnt(TreeNode *proot)//获取二叉树层数
{
	if (NULL == proot)
	{
		return 0;
	}
	int cntl = get_tree_layer_cnt(proot->pl);
	int cntr = get_tree_layer_cnt(proot->pr);

	return cntl > cntr ? cntl+1 : cntr+1;
}

void destroy_tree(TreeNode *proot)//摧毁二叉树
{
	if (NULL == proot)
	{
		return ;
	}
	destroy_tree(proot->pl);
	destroy_tree(proot->pr);
	free(proot);
}

void layer_order(TreeNode *proot)//层序遍历
{
	DataType outdata;
	QueList *pque = create_queue();	
	if (NULL == pque)
	{
		return ;
	}
	
	push_queue(pque, proot);

	while (!is_empty_queue(pque))
	{
		pop_queue(pque, &outdata);
		printf("%c", outdata->data);
		if (outdata->pl != NULL)
		{
			push_queue(pque, outdata->pl);
		}
		if (outdata->pr != NULL)
		{
			push_queue(pque, outdata->pr);
		}
	}
	
	destroy_queue(pque);
}

6.4 queue.h

#ifndef __QUEUE_H__
#define __QUEUE_H__

#include "tree.h"

typedef TreeNode* DataType;

typedef struct que_node
{
	DataType data;
	struct que_node *pnext;
}QueNode;

typedef struct que_list
{
	QueNode *pfront;
	QueNode *prear;
	int clen;
}QueList;

extern QueList *create_queue();
extern int push_queue(QueList *, DataType );
extern int pop_queue(QueList *, DataType *);
extern int get_queue_front(QueList *, DataType *);
extern void destroy_queue(QueList *);
extern void clear_queue(QueList *);
extern int is_empty_queue(QueList *pque);

#endif

6.5 queue.c

#include "queue.h"
#include <stdlib.h>
#include <stdio.h>

QueList *create_queue()
{
	QueList *pque = malloc(sizeof(QueList));
	if (NULL == pque)
	{
		perror("fail malloc");
		return NULL;
	}
	pque->pfront = NULL;
	pque->prear = NULL;
	pque->clen = 0;

	return pque;
}

int is_empty_queue(QueList *pque)
{
	if (NULL == pque->pfront)
	{
		return 1;
	}
	return 0;
}

int push_queue(QueList *pque, DataType data)
{
	QueNode *pnode = malloc(sizeof(QueNode));
	if (NULL == pnode)
	{
		perror("fail malloc");
		return -1;
	}
	pnode->data = data;
	pnode->pnext = NULL;
	
	if (is_empty_queue(pque))
	{
		pque->pfront = pnode;
		pque->prear = pnode;
	}
	else
	{
		pque->prear->pnext = pnode;
		pque->prear = pnode;
	}
	pque->clen++;

	return 0;
}

int pop_queue(QueList *pque, DataType *pdata)
{
	if (is_empty_queue(pque))
	{
		return 1;
	}
	
	QueNode *pfree = pque->pfront;
	pque->pfront = pfree->pnext;
	if (pdata != NULL)
	{
		*pdata = pfree->data;
	}
	free(pfree);
	pque->clen--;
	if (NULL == pque->pfront)
	{
		pque->prear = NULL;
	}
	return 0;
}

int get_queue_front(QueList *pque, DataType *pdata)
{
	if (is_empty_queue(pque))
	{
		return -1;
	}
	*pdata = pque->pfront->data;

	return 0;
}

void destroy_queue(QueList *pque)
{
	clear_queue(pque);
	free(pque);
}

void clear_queue(QueList *pque)
{
	while (!is_empty_queue(pque))
	{
		pop_queue(pque, NULL);
	}
}

        注意：链式队列实现二叉树层序遍历的方法

                1. 创建二叉树

                2. 将二叉树的根节点入队

                3. 将根节点出队，打印根节点数据，并分别将根节点的左、右子树节点入队

                4. 将根节点左节点出队，打印左节点数据，并将根节点左节点的左右节点入队

                5. 循环上述操作直到遍历结束

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1872255.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

微机原理与接口技术：重点内容｜计算机系统｜学习笔记

微机原理与接口技术：重点内容｜计算机系统｜学习笔记

系列目录 前言 只将最重要的知识点考点列出来方便学习复习 目录 系列目录前言第1章 微型计算机概述第2章 16位和32位微处理机&#x1f31f;16位微处理器 8086 第3章 Pentium 的指令系统常用指令 第4章 存储器、存储管理和高速缓存技术第5章 微型计算机和外设的数据传输第6章 串…
阅读更多...
ollama大模型qwen2:7b性能测试

ollama大模型qwen2:7b性能测试

部署環境信息&#xff1a; (base) rootalg-dev17:/opt# lscpu Architecture: x86_64CPU op-mode(s): 32-bit, 64-bitAddress sizes: 45 bits physical, 48 bits virtualByte Order: Little Endian CPU(s): 8On-line CP…
阅读更多...
Application Studio 学习笔记（3）

Application Studio 学习笔记（3）

一、工具栏按钮 1、panel控件添加工具栏按钮 展开panel控件的Advanced属性并点击Action Data&#xff0c;进入Action Data编辑界面 新增Action Data数据&#xff0c;Sequence设定工具按钮的显示顺序 默认工具按钮会显示在弹出工具栏中 勾选Add to Primary ToolBar后&#xff…
阅读更多...
电容式单按键触摸检测及接近感应控制芯片 SD8233LQG

电容式单按键触摸检测及接近感应控制芯片 SD8233LQG

SD8233LQG是一款电容式单按键触摸检测及接近感应控制芯片。采用 CMOS 工艺制造&#xff0c;内建稳压和去抖动电路&#xff0c;高可靠性&#xff0c;专为取代传统按键开关而设计。超低功耗与宽工作电压特性&#xff0c;广泛应用于 TWS及 DC 应用的触摸产品中&#xff0c;实现产品…
阅读更多...
vue3 中的根据某些特定的文字来筛选数组数据

vue3 中的根据某些特定的文字来筛选数组数据

现在有一批这样的数据 这样的数据 我想根据 hallName 来筛选数据 比如关键字有 我不需要 带有下面字符换的数组数据 const importantData ref(["VIP", "CINITY", "杜比", "IMAX", "4DX", vip, Vip]) 使用some 方法 arr…
阅读更多...
笔记-python爬虫概述

笔记-python爬虫概述

目录 常用第三方库 爬虫框架 动态页面渲染1. url请求分析2. selenium3. phantomjs4. splash5. spynner 爬虫防屏蔽策略1. 修改User-Agent2. 禁止cookies3. 设置请求时间间隔4. 代理IP池5. 使用Selenium6. 破解验证码常用第三方库 对于爬虫初学者&#xff0c;建议在了解爬虫原…
阅读更多...
FFmpeg中位操作相关的源码：GetBitContext结构体，init_get_bits函数、get_bits1函数和get_bits函数分析

FFmpeg中位操作相关的源码：GetBitContext结构体，init_get_bits函数、get_bits1函数和get_bits函数分析

一、引言 由《音视频入门基础&#xff1a;H.264专题&#xff08;3&#xff09;——EBSP, RBSP和SODB》可以知道&#xff0c;H.264 码流中的操作单位是位(bit)&#xff0c;而不是字节。因为视频的传输和存贮是十分在乎体积的&#xff0c;对于每一个比特&#xff08;bit&#xf…
阅读更多...
CentOS安装Docker教程（包含踩坑的经验）

CentOS安装Docker教程（包含踩坑的经验）

目录 一.基础安装 ▐ 安装Docker 二.启动Docker服务 三.配置Docker镜像加速 一.基础安装 在安装Docker之前可能需要先做以下准备 首先如果系统中已经存在旧的Docker&#xff0c;则先卸载&#xff1a; yum remove docker \docker-client \docker-client-latest \docker-…
阅读更多...
Modbus转Profibus网关在汽车行业的应用

Modbus转Profibus网关在汽车行业的应用

一、前言 在当前汽车工业的快速发展中&#xff0c;汽车制造商正通过自动化技术实现生产的自动化&#xff0c;目的是提高生产效率和减少成本。Modbus转Profibus网关&#xff08;XD-MDPB100&#xff09;应用于汽车行业&#xff0c;主要体现在提升自动化水平、优化数据传输以及实…
阅读更多...
Java8新特性stream的原理和使用

Java8新特性stream的原理和使用

这是一种流式惰性计算&#xff0c;整体过程是&#xff1a; stream的使用也异常方便&#xff0c;可以对比如List、Set之类的对象进行流式计算&#xff0c;挑出最终想要的结果&#xff1a; List<Timestamp> laterTimes allRecords.stream().map(Record::getTime).filter…
阅读更多...
第11章 规划过程组（收集需求）

第11章 规划过程组（收集需求）

第11章 规划过程组&#xff08;一&#xff09;11.3收集需求&#xff0c;在第三版教材第375~378页&#xff1b; 文字图片音频方式 第一个知识点&#xff1a;工具与技术 1、决策 投票 用于生成、归类和排序产品需求 独裁型决策制定 一个人负责为整个集体制定决策 多标准决策分析…
阅读更多...
软件需求管理规程（DOC原件）

软件需求管理规程（DOC原件）

软件需求管理规程是确保软件开发过程中需求清晰、一致、可追踪的关键环节&#xff1a; 明确需求&#xff1a;项目初期&#xff0c;与利益相关者明确项目目标和需求&#xff0c;确保需求完整、无歧义。需求评审&#xff1a;组织专家团队对需求进行评审&#xff0c;识别潜在风险和…
阅读更多...
DM达梦数据库存储过程

DM达梦数据库存储过程

&#x1f49d;&#x1f49d;&#x1f49d;首先&#xff0c;欢迎各位来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里不仅可以有所收获&#xff0c;同时也能感受到一份轻松欢乐的氛围&#xff0c;祝你生活愉快&#xff01; &#x1f49d;&#x1f49…
阅读更多...
Arduino - OLED

Arduino - OLED

Arduino - OLED Arduino - OLED Arduino通过u8g2库驱动OLEDU8g2 驱动oled自定义中文字库 The OLED (Organic Light-Emitting Diode) display is an alternative for LCD display. The OLED is super-light, almost paper-thin, flexible, and produce a brighter and crisper…
阅读更多...
【乐吾乐2D可视化组态编辑器】图形库、组件库

【乐吾乐2D可视化组态编辑器】图形库、组件库

15 图形库 15.1 图纸 新建文件夹、新建图纸、删除文件夹、删除图纸 15.2 系统组件 乐吾乐图形库一共分为三大类&#xff1a;基础图形库、电力图形库、物联网图形库、2.5D图形库&#xff0c;总共约4000个图元&#xff0c;能满足大部分行业的基本需求。 格式有三种&#xff1a…
阅读更多...
智慧法务引领：构筑数字化法治核心，塑造未来企业竞争力

智慧法务引领：构筑数字化法治核心，塑造未来企业竞争力

在全球化及信息化时代背景下&#xff0c;企业面临的法律环境越来越复杂&#xff0c;法治数字化成为企业维护合法权益、提升市场竞争力的必然选择。智慧法务管理系统作为推动企业法治数字化转型的重要工具&#xff0c;不仅提高了法律服务效率&#xff0c;而且加强了企业的法律风…
阅读更多...
百问网全志D1h开发板投屏功能实现

百问网全志D1h开发板投屏功能实现

投屏功能实现 D1系列号称点屏神器&#xff0c;不仅能点屏&#xff0c;还能用于投屏。 源码准备 百问网为 【百问网D1h开发板】提供了投屏功能需要使用的源码&#xff0c;直接git下载即可&#xff1a; git clone https://github.com/DongshanPI/DongshannezhaSTU_DLNA_Scree…
阅读更多...
MoneyPrinterPlus:AI自动短视频生成工具-微软云配置详解

MoneyPrinterPlus:AI自动短视频生成工具-微软云配置详解

MoneyPrinterPlus可以使用大模型自动生成短视频&#xff0c;我们可以借助Azure提供的语音服务来实现语音合成和语音识别的功能。 Azure的语音服务应该是我用过的效果最好的服务了&#xff0c;微软还得是微软。 很多小伙伴可能不知道应该如何配置&#xff0c;这里给大家提供一…
阅读更多...
沉淀强化镍基合金660大螺丝的物理性能

沉淀强化镍基合金660大螺丝的物理性能

沉淀强化镍基合金660大螺丝&#xff0c;是一种高性能的工程材料&#xff0c;其在极端环境中展现了优异的稳定性和耐用性。以下&#xff0c;我们将深入解析其主要的物理性能。 首先&#xff0c;该合金螺丝的密度为7.99g/cm&#xff0c;这意味着它具有较高的质量密度&#xff0c;…
阅读更多...
力扣随机一题 6/28 数组/矩阵

力扣随机一题 6/28 数组/矩阵

&#x1f4dd;个人主页&#x1f339;&#xff1a;誓则盟约⏩收录专栏⏪&#xff1a;IT 竞赛&#x1f921;往期回顾&#x1f921;&#xff1a;6/27 每日一题关注博主&#xff0c;后期持续更新系列文章如果有错误感谢请大家批评指出&#xff0c;及时修改感谢大家点赞&#x1f44d…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023