1.首先示例图为例：

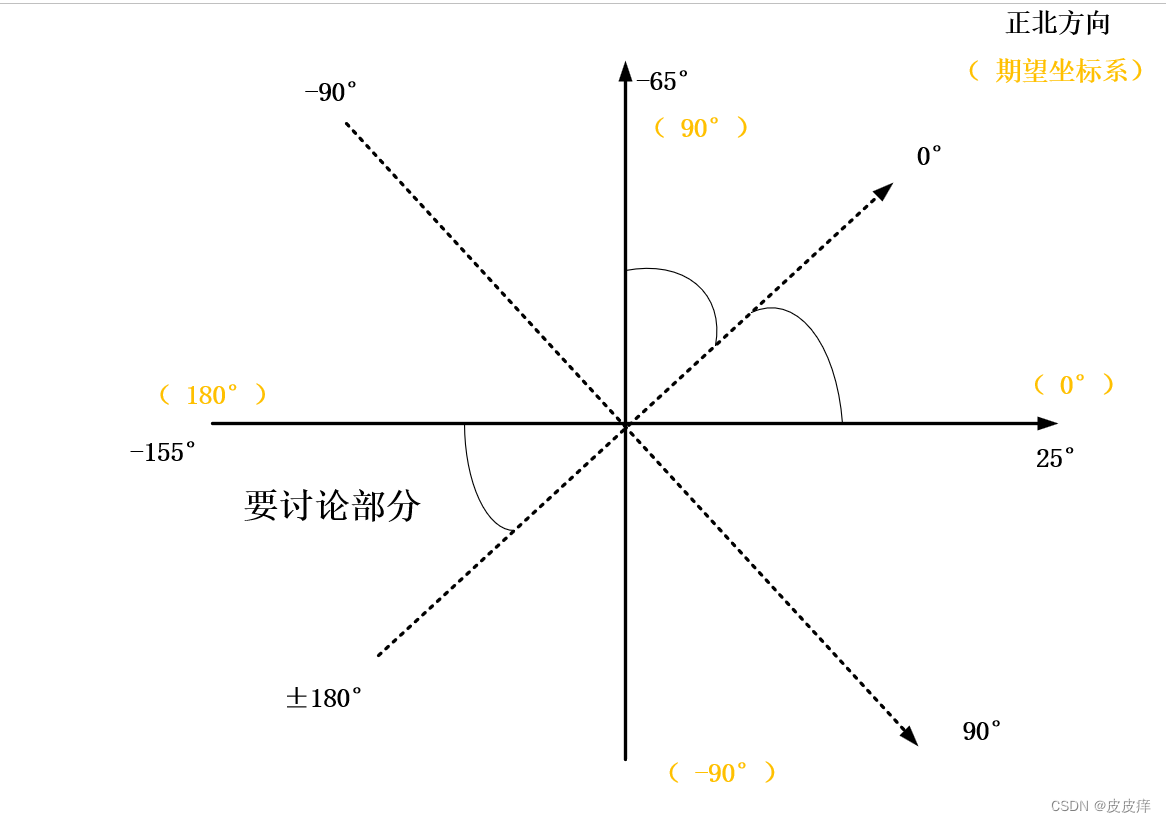
虚线黑色角度为IMU的坐标系；实线为自定义坐标系；
矫正：（默认angleyaw为IMU采的数据角度）

    angleyaw_pt = angleyaw-25;
  if(-180<angleyaw&&angleyaw<-155)    // 角度跳变问题（超出180范围）
  {
	  angleyaw_pt=angleyaw_pt+360;
	  
  }
  // 看需求转化方向
  angleyaw_pt=angleyaw_pt+180;
  if(angleyaw_pt>180)   
  {
	  angleyaw_pt=angleyaw_pt-360;
	  
  }