目录
1.线性规划问题举隅
（1）问题介绍
（2）问题分析
（3）灵敏度分析
（4）方法缺陷
（5）可行域&凸集
2.lingo的简单认识
（1）默认设置
（2）运行按键
（3）运行窗口
（4）总结提炼
（5）激活全局求解器
3.灵敏度分析
（1）案例分析
（2）注意事项
4.二次规划
（1）问题介绍
（2）程序部分
（3）相关说明
下集预告--集合~属性~~指派集合~~~~
1.线性规划问题举隅
（1）问题介绍
（2）问题分析
这个就是一个生产奶制品的问题，一桶牛奶有两种选择，一种就是生产3公斤的A1奶制品，一种就是生产4公斤的A2奶制品，480指的是这个所有工人的总的工作时长，A1这个奶制品最多生产100公斤，一共是有50桶牛奶作为原料，求解这个最大利润的生产方案；
（3）灵敏度分析
上面的这个小三问实际上就是和这个灵敏度分析相关的，这个灵敏度分析在数学建模里面不是不可少的，但是这个写好了就是我们的论文的亮点，但是实际上大部分参加比赛的同学都是在这个灵敏度分析部分不疼不痒的写上几句话，这个其实是我们需要学习的地方，通过这三个小问我们简单的认识一下这个灵敏度分析的过程；
（4）方法缺陷
上面的这个就是决策变量和目标函数以及约束条件，下面的是使用的图解法进行求解的，这个实际上我们高中阶段是学习过的，但是这个方法的缺点就是只能解决二元的归化问题，因为这个要画图，如果这个变量的个数超过两个，这个图就不好画，画了也不直观；
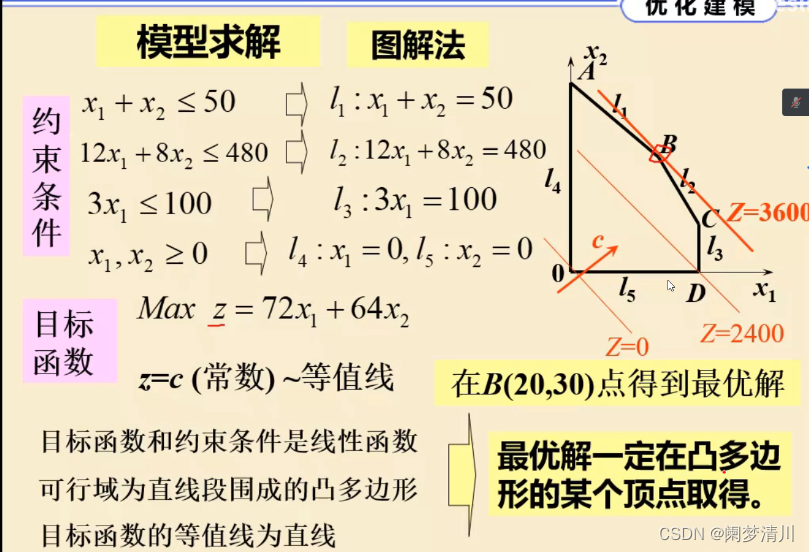
（5）可行域&凸集
图解法的最优解一定是在端点位置取到的，这个可行域我们也称之为凸集；
2.lingo的简单认识
（1）默认设置
简单的一个例子：以model开始，以end结束，先写目标函数，后写约束条件；我们没有把这个x,y>=0写进去是因为这个lingo里面的变量默认都是大于0的，我们后面如果想要取消这个默认限制，可以使用free函数，取消这个变量大于0的默认设置；
（2）运行按键
运行窗口介绍，我们可以点击这个solve命令里面的solve命令，也可以直接使用这个工具栏里面的类似于扎飞镖的小标志，都是可以运行这个程序的；
（3）运行窗口
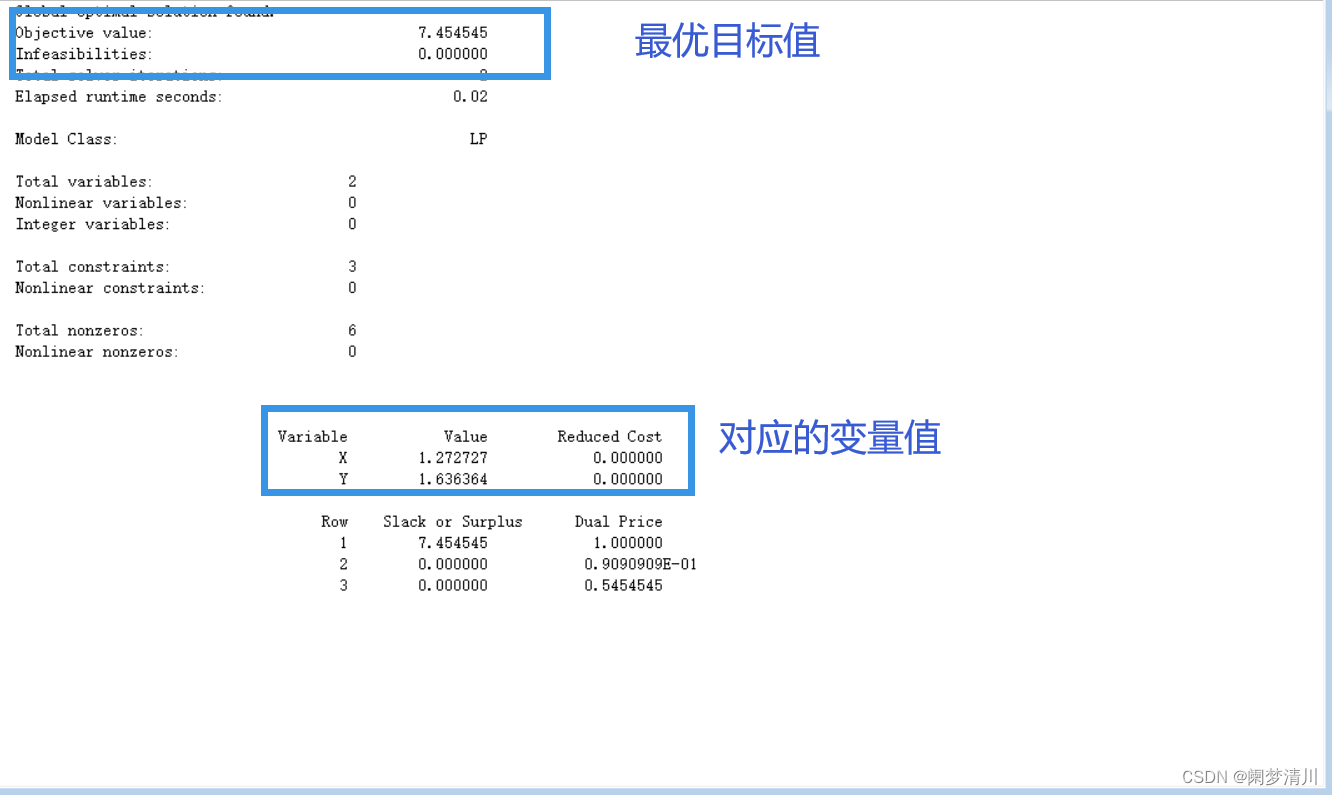
运行之后会弹出来两个窗口，一个就是下面的这个，里面有一些参数说明，可以简单的了解一下；
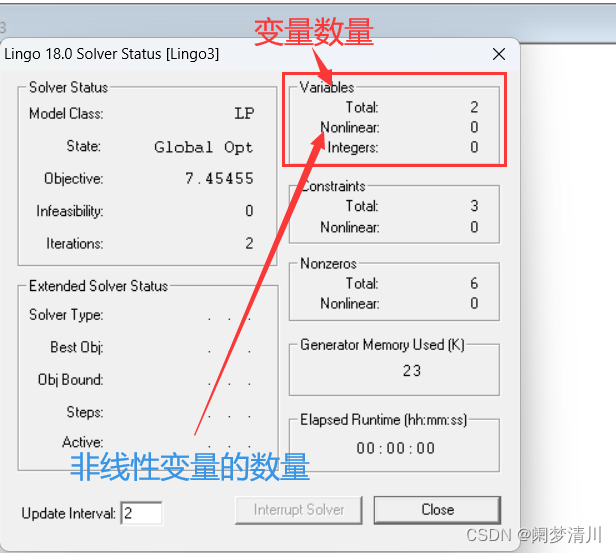
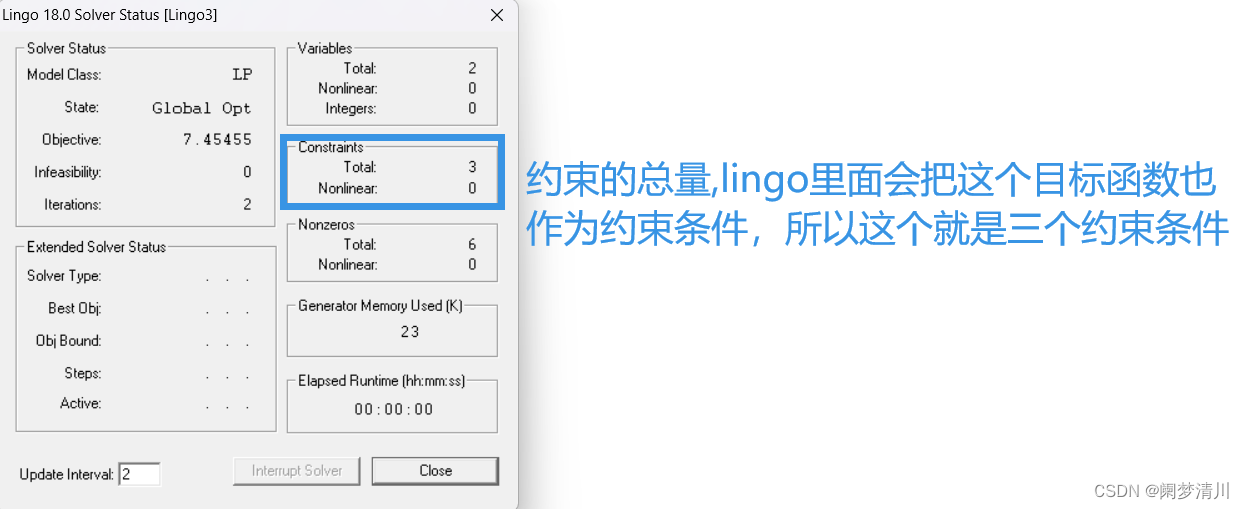
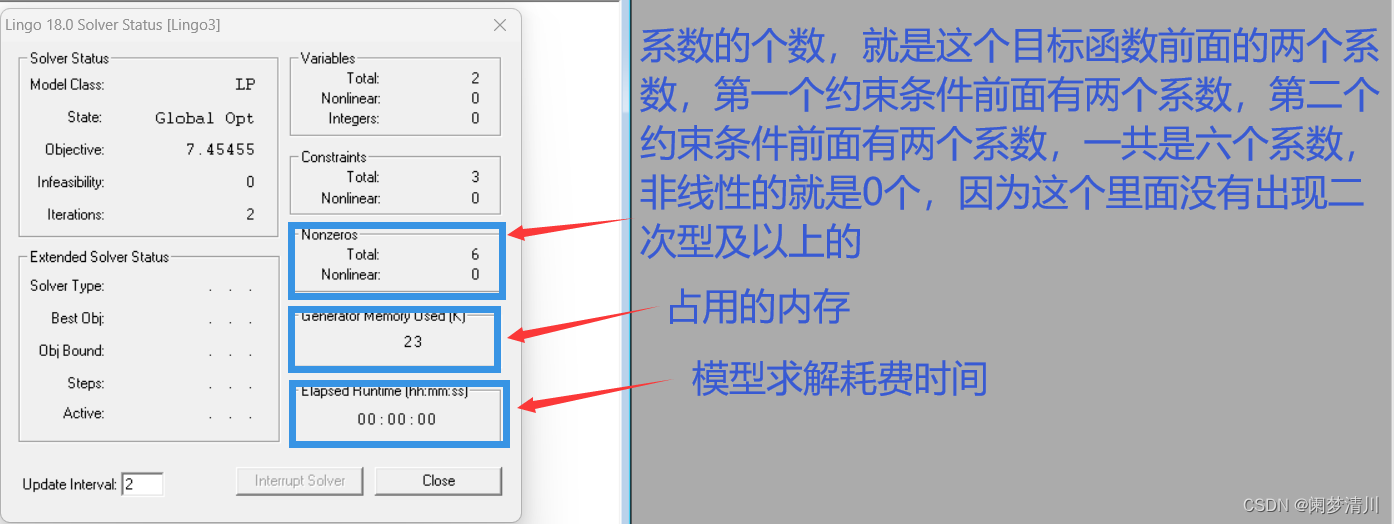
（4）总结提炼
实际上在建模里面，我们是一般不会很留意这个第一个相关设置的窗口的，像这个里面的变量的个数，占用内存这些我们不会关心，我们只需要关注第二个窗口里面的目标函数最优值以及这个相关决策变量的取值；
（5）激活全局求解器
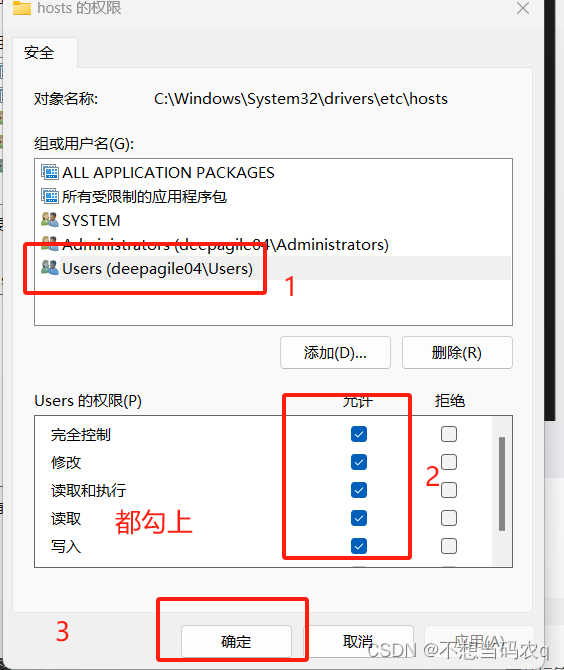
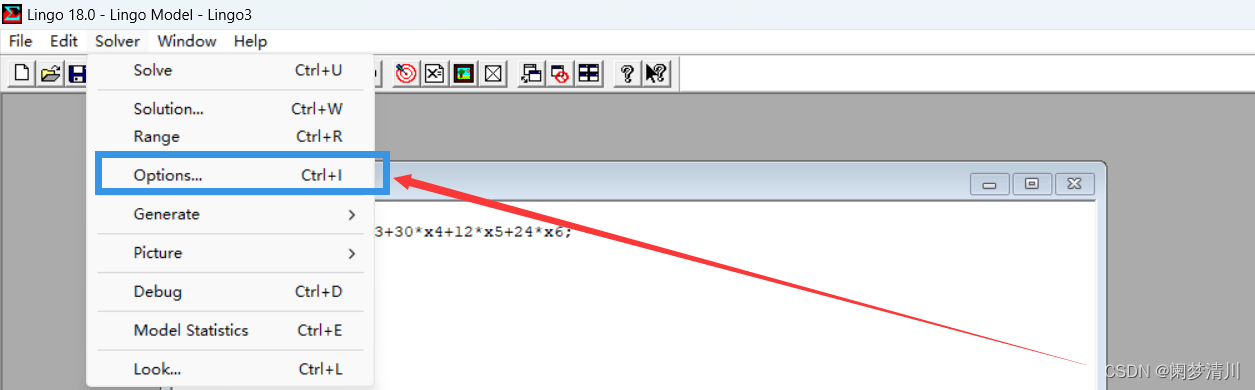
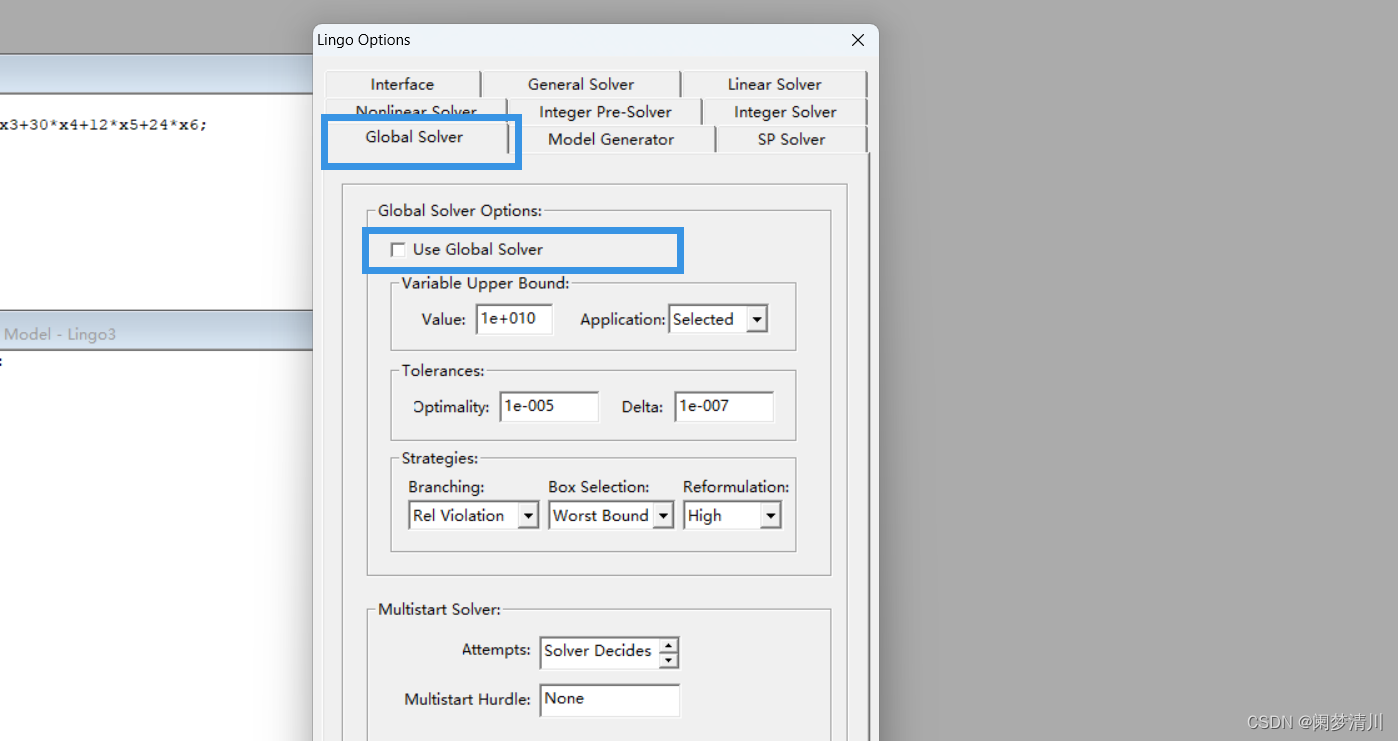
这个就是对于一些规划问题，我们为了避免程序找到局部最优解就停止，而是让这个程序找到全局最优解，这个时候我们需要激活相关的设置；点击options------点击global solver------点击这个use前面的勾选按钮；
3.灵敏度分析
（1）案例分析
这个灵敏度分析lingo求解的时候是会进行分析的，但是这个不会显示，我们仔细如果需要的话就需要我们自己手动的调出来；
我们通过一个案例认识一下这个灵敏度分析：
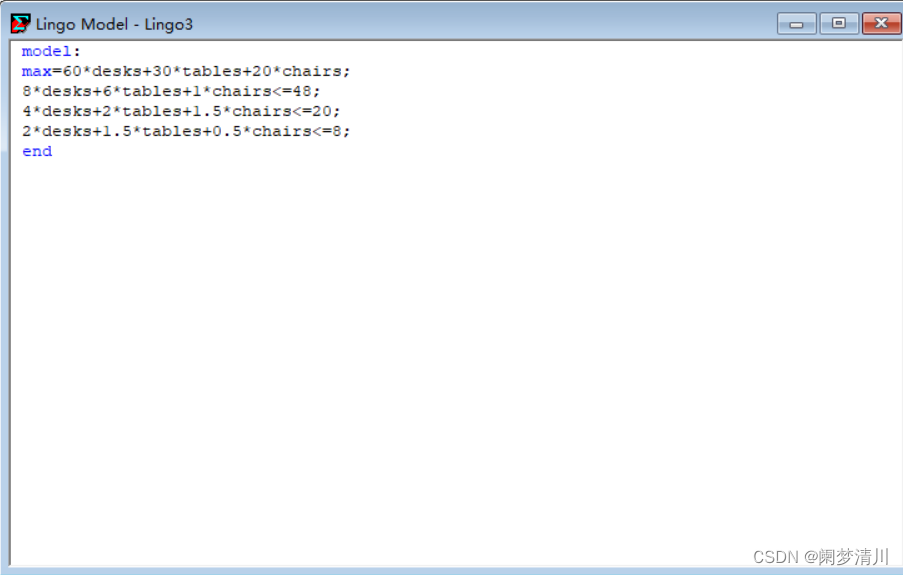
求解程序：
选择这个灵敏度分析，先进行下面的设置，还是在options里面，选择这个price&ranges选项，表示完成设置，然后把这个程序重新运行一遍；
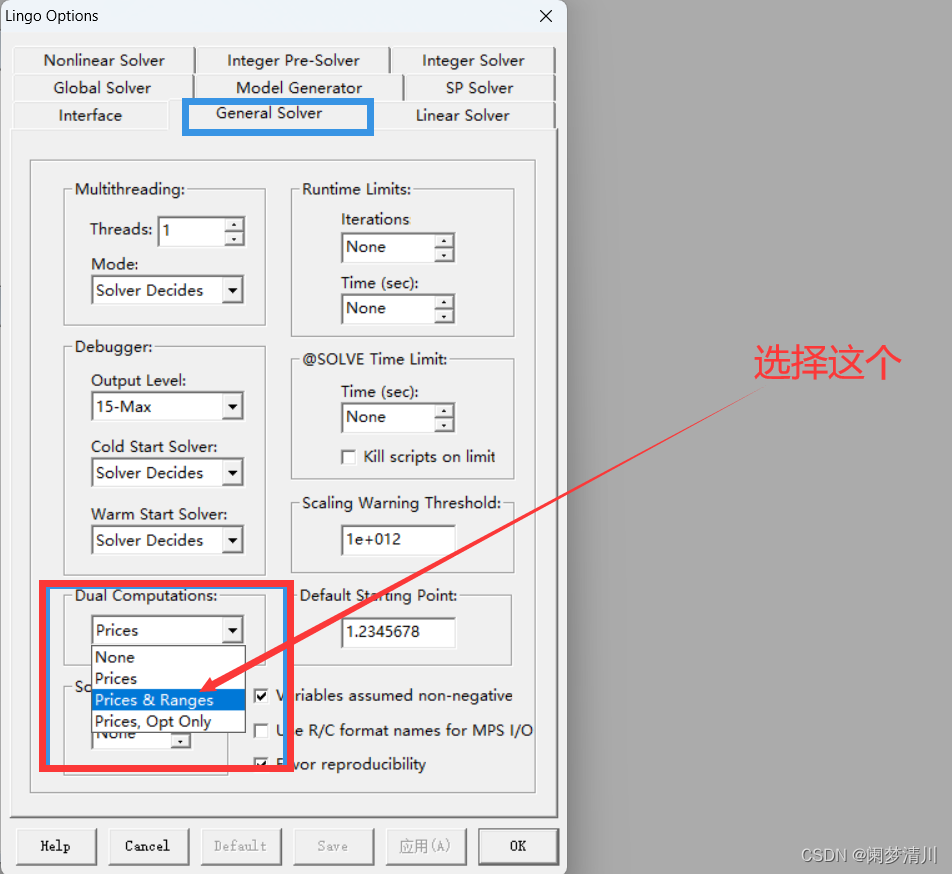
程序重新运行一遍之后，点击这个solvers里面的range选项，就可以看到下面的页面选项：
上面的表显示的就是这个变量的变化范围，什么是灵敏度分析，灵敏度分析就是系数的变化范围，在这个范围里面变化不会影响到最优解，但是会影响最优值，以这个里面的desk一行为例子，这个原本的系数是60（见下图），现在灵敏度分析告诉我们，这个可以向上浮动20，向下浮动4，也就是在56~80之间变化都不会影响这个最优解，最优解就是这个生产几个桌子，几个凳子，几个椅子，原来是几个，在这个56~80的范围里面还是几个，这个最优解是不会改变的，但是最优值会改变，因为这个决策变量系数都变化了；
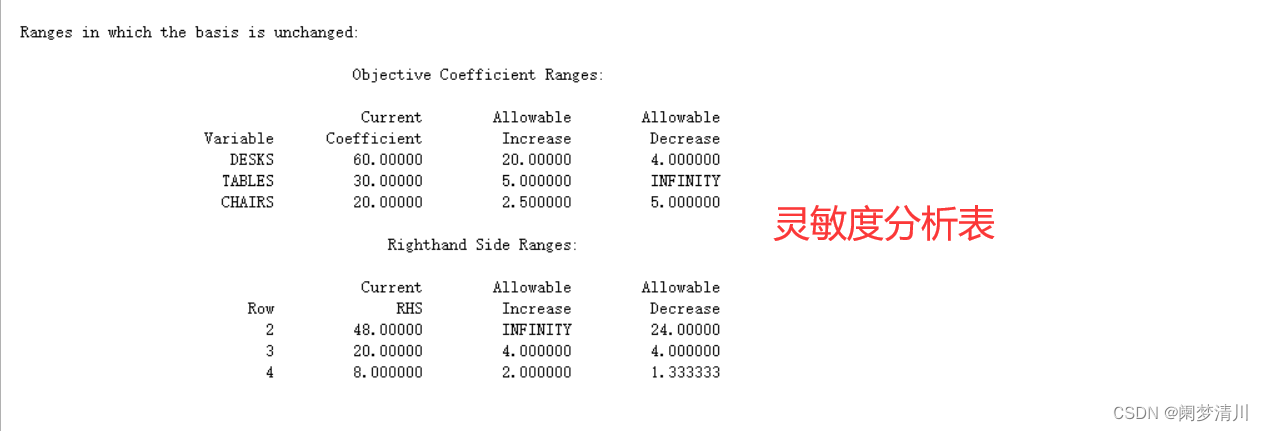下面的表格表示的就是这个约束条件灵敏度分析，2这一行就是第一个约束条件，因为这个lingo把这个目标函数当成了第一个约束条件；
原来的约束条件是<=48,现在是可以在负无穷到72（48+24）之间进行浮动，那个infinity就是表示的负无穷，这个范围里面变化时候不会影响到最优值，因为这个时候系数也没有改变，所以这个时候的最优解也是没有变化的；
以上就是这个案例的灵敏度分析的过程，相信你通过这个题目会对灵敏度分析有一个立体的认识；
（2）注意事项
因为这个灵敏度分析是我们自己手动调用的，但是这个会影响我们的程序的运行效率，延长运行时间，因此我们平常不使用的时候不会进行相关的设置；
4.二次规划
（1）问题介绍
二次规划就是这个问题里面的决策变量的次数是二次的，像下面的这个里面的x1的平方，x2的平方等等，s.t表示的就是约束条件，其中这个问题里面要求这个决策变量必须是整数，这个时候需要使用一个函数grim函数
（2）程序部分
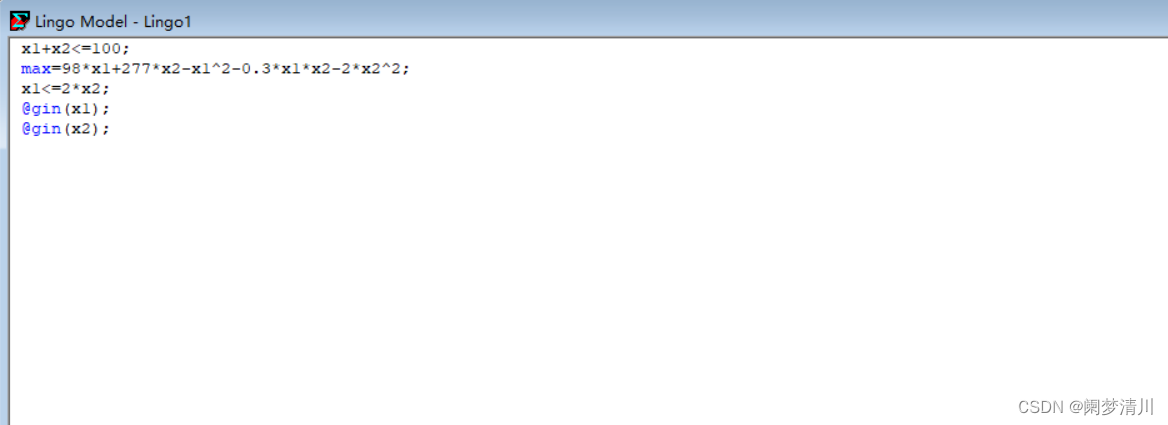
（3）相关说明
第一个就是这个语句的位置对于我们整个程序没有影响，因此我们上面的程序把这个max函数放在了第二行，但是我们一般不会这么搞，只是让大家知道这个是可以的；
gin是取整函数，free是解除限制函数（默认的一些设置），BND函数，就是如果我们已经知道了这个变量的范围，我们就可以使用这个函数告诉系统这个变量的搜索区间，减少这个时间的消耗，上面的批注里面有一个实例，就是我们知道这个x1变量的范围是1~10，我们就可以写做这个BND（1，x1,10），bin函数针对于01规划使用的；
