目录
- 机器学习 - 概率图模型 之 隐马尔可夫模型 HMM
- 一、马尔科夫链
- 二、HMM 的基本概念
- 1、HMM 背景与定义
- 2、HMM 的两个基本假设
- 3、确定 HMM 的两个空间和三组参数
- 三、HMM 三个基本问题 | 导图
- 四、HMM 相关算法
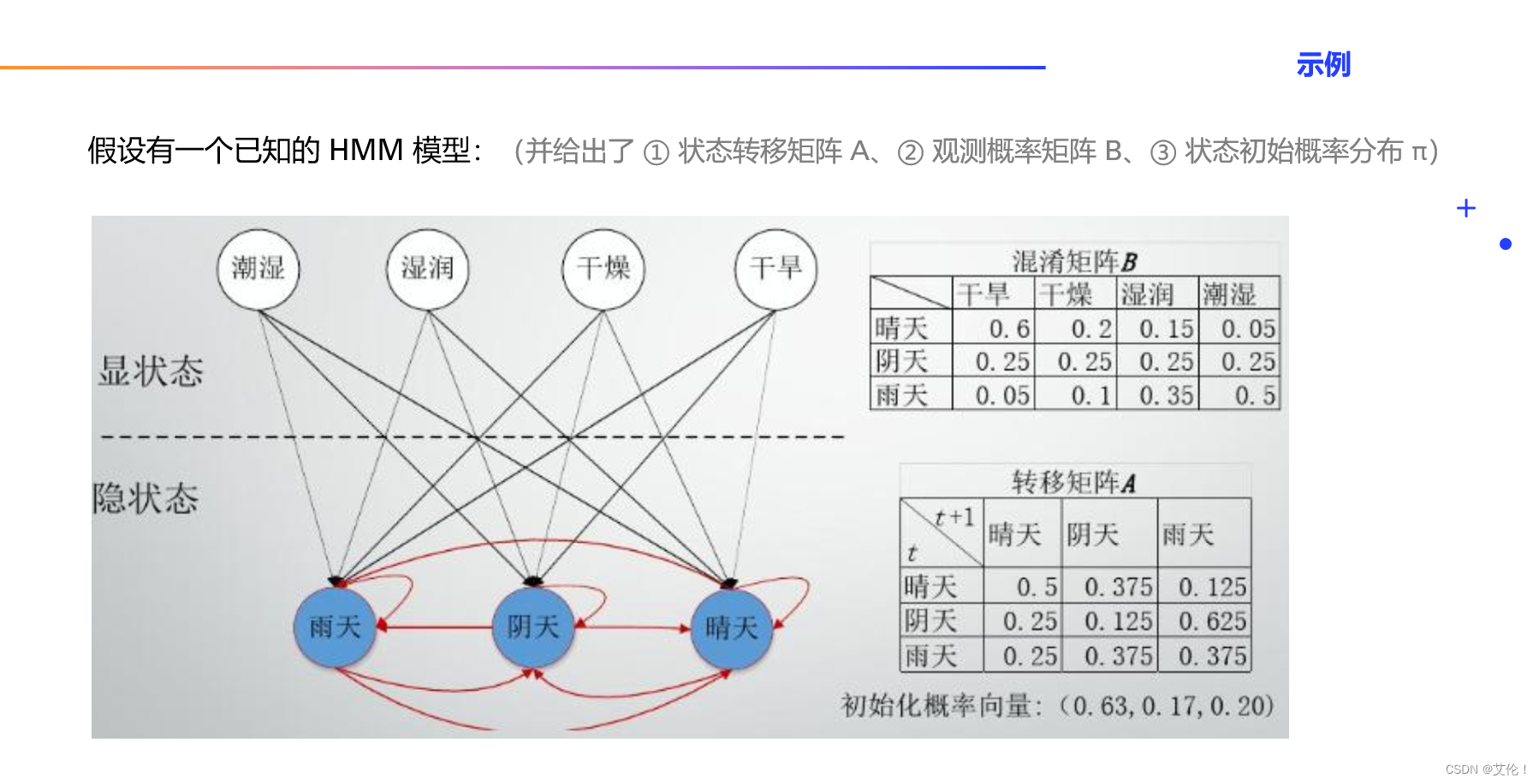
- 1、前向算法
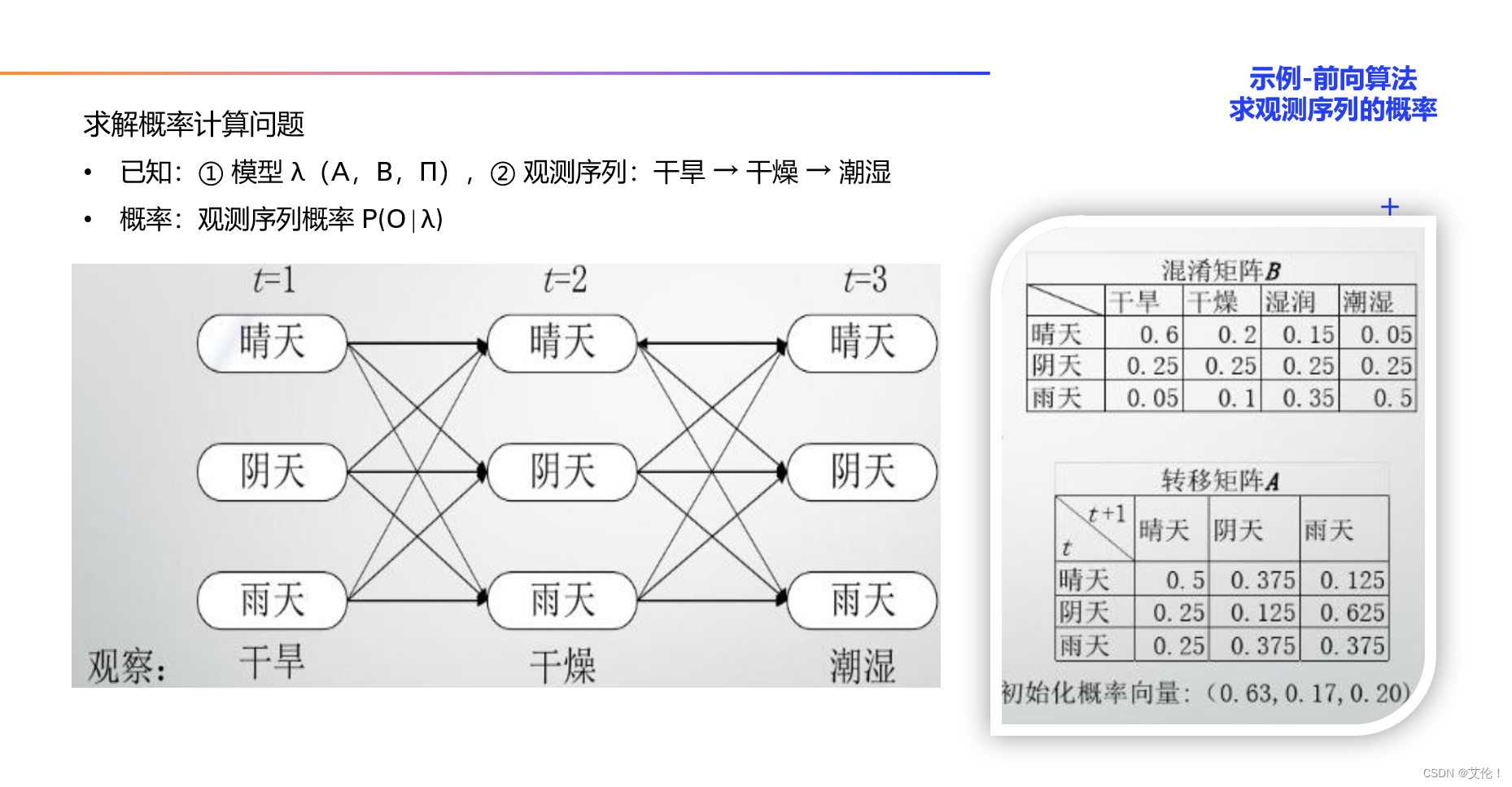
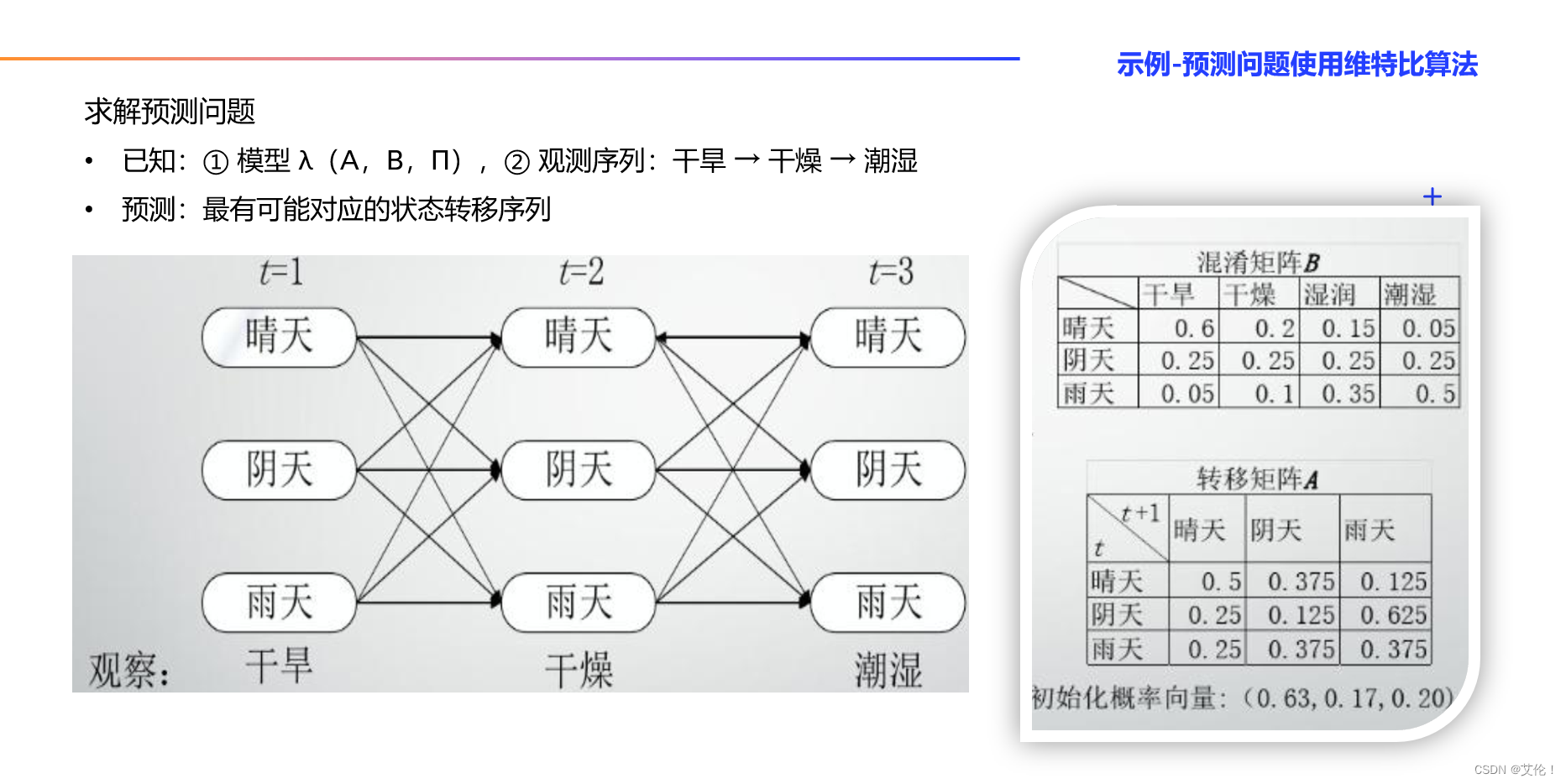
- 2、维特比(Viterbi)算法
- 五、案例:Viterbi 算法的代码实现
机器学习 - 概率图模型 之 隐马尔可夫模型 HMM
一、马尔科夫链
回顾:概率图模型的分类
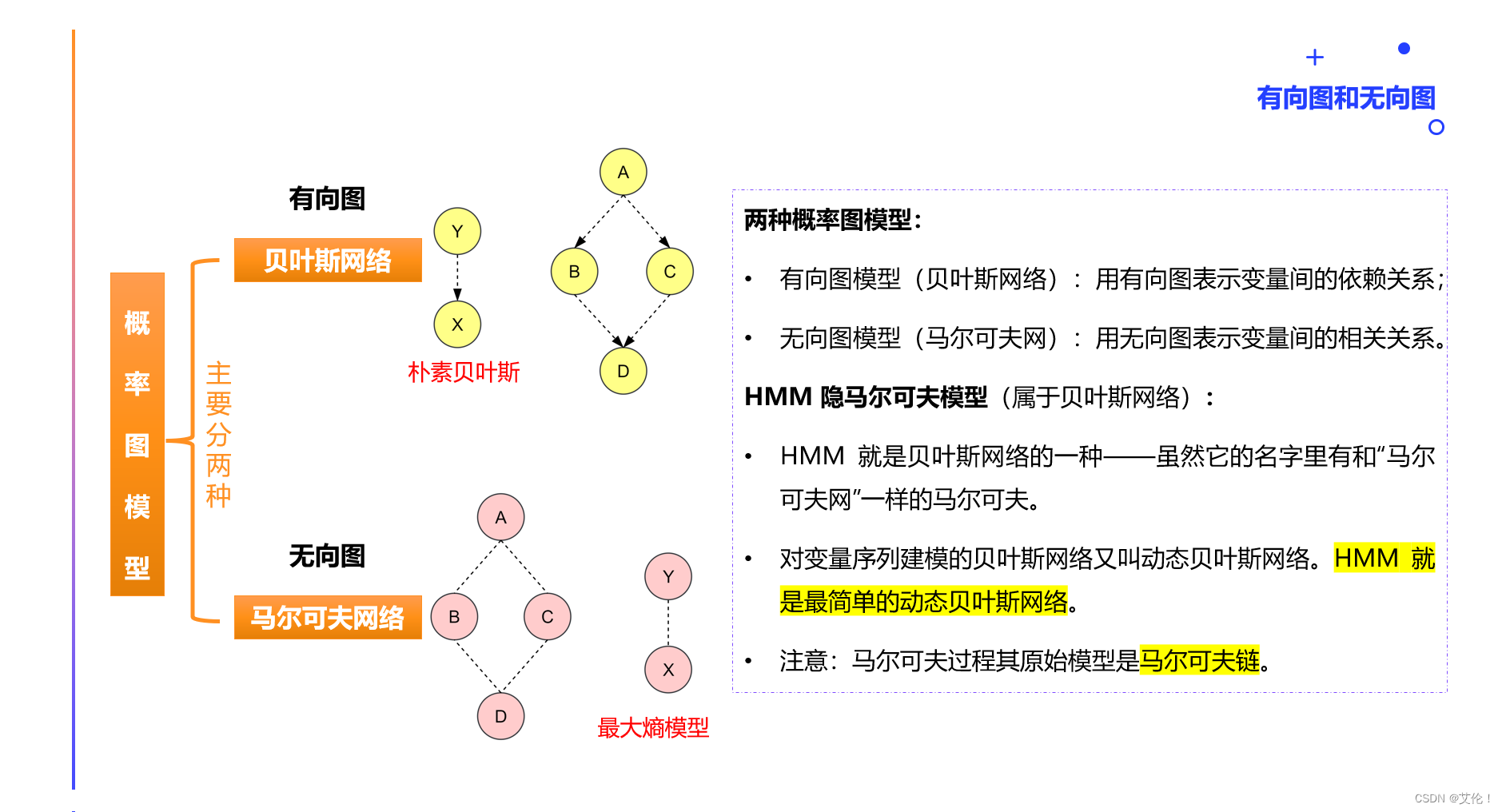
- HMM(隐马尔可夫模型)属于贝叶斯网络(有向图模型)的一种——是最简单的动态贝叶斯网络。
马尔可夫过程(Markov Processes)

-
定义:假设一个随机过程中, t n t_n tn 时刻的状态 s n s_n sn 的条件分布,仅仅与其前一个状态 s n − 1 s_{n-1} sn−1 有关,即 P ( s n ∣ s 1 , s 2 , … , s n − 1 ) = P ( s n ∣ s n − 1 ) P(s_n|s_1,s_2,\ldots,s_{n-1})=P(s_n|s_{n-1}) P(sn∣s1,s2,…,sn−1)=P(sn∣sn−1) ,则将其称为马尔可夫过程。
-
特性:在已知系统当前状态的条件下,它未来的演变不依赖于过去的演变。
- 也就是说,一个马尔可夫过程可以表示为:系统在状态转移过程中,第 t+1 次结果只受第 t 次结果的影响,即只与当前状态有关,而与过去状态(系统的初始状态和此次转移前的所有状态)无关。
-
注意:马尔可夫过程其原始模型是马尔可夫链。
马尔科夫链(Markov Chain)

- 定义:时间、状态都是离散的马尔可夫过程称为马尔可夫链。
- 注意:隐马尔可夫模型是对含有未知参数(隐变量)的马尔科夫链进行建模的生成模型。
二、HMM 的基本概念
1、HMM 背景与定义
提出背景

HMM 的定义
-
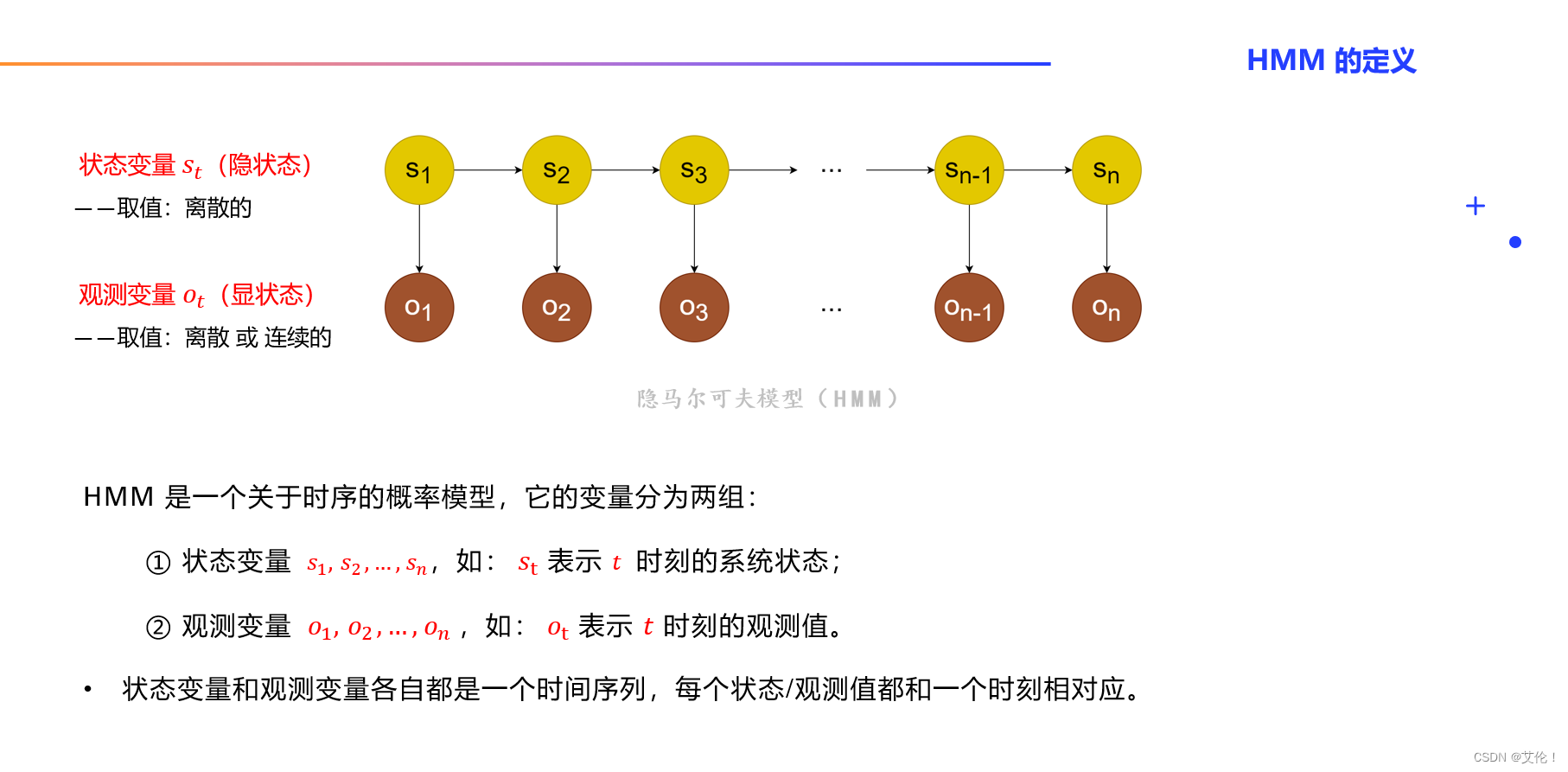
隐马尔可夫模型(Hidden Markov Model, HMM)描述由隐藏的马尔科夫链生成观测序列的过程:
- 一条隐藏的马尔可夫链随机生成了一个不可观测的状态序列(state sequence);
- 然后每个状态又对应生成了一个观测结果,这些观测值按照时序排列后就成了观测序列(observation sequence)。
- 这两个序列(状态序列、观测序列)是一一对应的,每个对应的位置又对应着一个时刻。
-
HMM 是一个关于时序的概率模型,它的变量分为两组:
- ① 状态变量 s 1 , s 2 , . . . , s n {s_1,s_2,...,s_n} s1,s2,...,sn,如: s t s_t st 表示 t t t 时刻的系统状态;
- ② 观测变量 o 1 , o 2 , . . . , o n {o_1,o_2,...,o_n} o1,o2,...,on,如: o t o_t ot 表示 t t t 时刻的观测值。
- 状态变量和观测变量各自都是一个时间序列,每个状态/观测值都和一个时刻相对应。
-
HMM(Hidden Markov Model)各字母的含义:
- 一般假定状态序列是隐藏的,不能被观测到的,因此状态变量是隐变量,这就是 HMM 中的 H(Hidden)的来源。
- 这个隐藏的,不可观测的状态序列是由一个马尔可夫链随机生成的,这是 HMM 中的第一个 M(Markov)的含义。
-
状态变量与观测变量的取值:
- 一般而言,HMM 的状态变量取值是离散的;而观测变量的取值,则可以是离散的,也可以是连续的。
- 不过为了方便讨论,也因为在大多数应用中观测变量也是离散的,因此,我们下面仅讨论状态变量和观测变量都是离散的情况。
2、HMM 的两个基本假设
两个假设:① 齐次马尔可夫假设、② 观测独立性假设

3、确定 HMM 的两个空间和三组参数
两个空间:① 状态空间 Q、② 观测空间 V

三组参数:① 状态初始概率分布 π、② 状态转移矩阵 A、③ 观测概率矩阵 B(又称:发射概率矩阵、混淆矩阵)

三、HMM 三个基本问题 | 导图
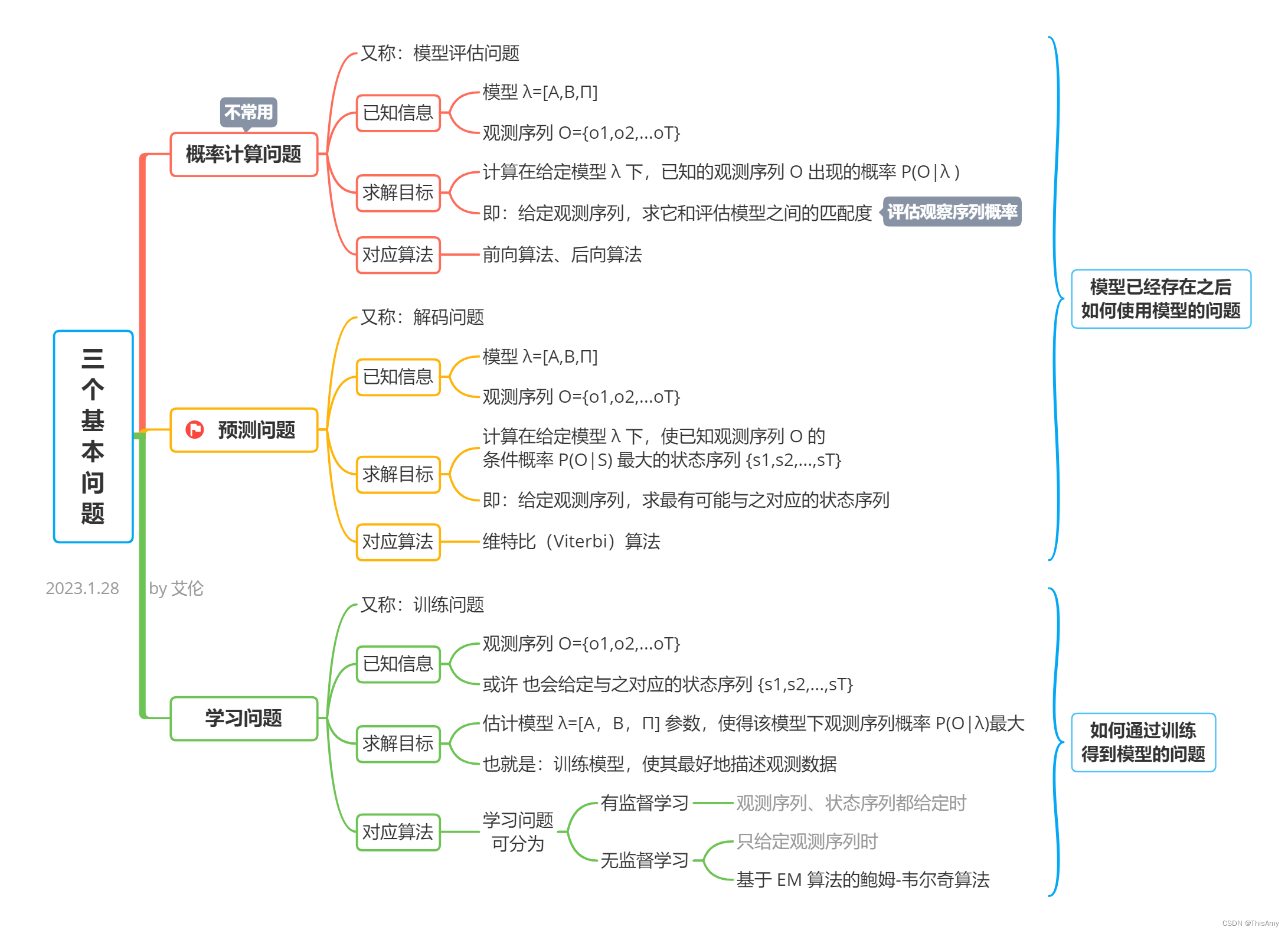
三个基本问题:① 概率计算问题、② 预测问题、③ 学习问题
导图:
四、HMM 相关算法
下面通过一个示例,分别使用前向算法求观测序列的概率、用维特比算法处理预测问题——目的:了解前向算法、维特比算法的思想
1、前向算法
导图:前向算法的流程梳理

示例:使用前向算法求 HMM 观测序列的概率




2、维特比(Viterbi)算法
导图:维特比算法的流程梳理

示例:维特比算法解码隐藏状态序列(预测问题)





五、案例:Viterbi 算法的代码实现
案例分析:

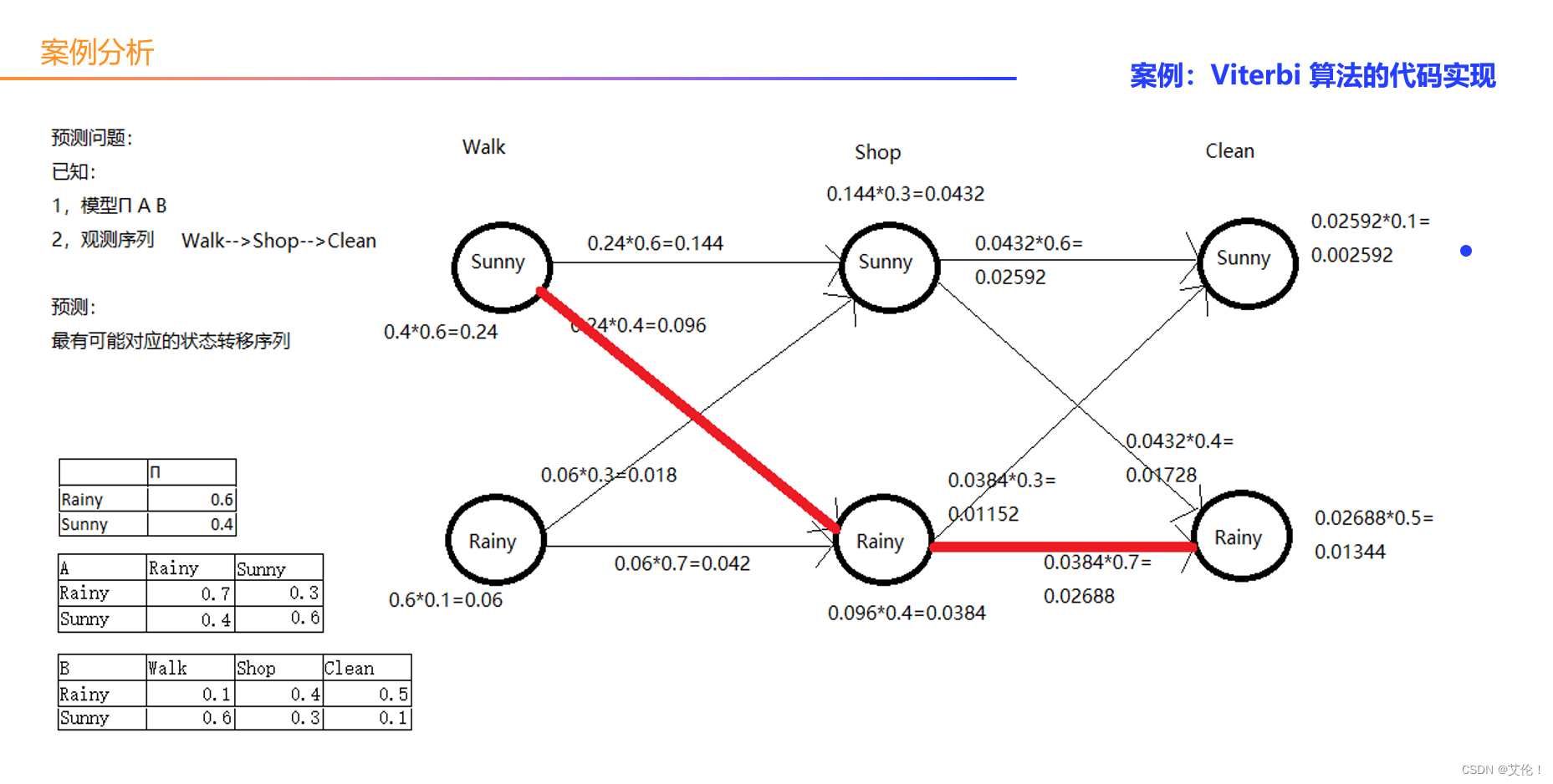
代码实现:( 工具:PyCharm,基于:python3)
"""
维特比(Viterbi)算法处理预测问题
⭐ 学习时间:2023.1.27
"""
def viterbi(obs, states, start_p, trans_p, emit_p):
"""
:param obs:观测序列
:param states:隐状态
:param start_p:初始概率(隐状态)
:param trans_p:转移概率(隐状态)
:param emit_p: 发射概率 (隐状态表现为显状态的概率)
:return:
"""
V = [{}] # 路径概率表 V[时间][隐状态] = 概率
path = {} # 一个中间变量,代表当前状态是哪个隐状态
# ------ 初始化初始状态 (t == 0) ------
for y in states:
V[0][y] = start_p[y] * emit_p[y][obs[0]]
path[y] = [y]
print(V[0])
print(path)
# ------ 对 t > 0 跑一遍维特比算法 ------
for t in range(1, len(obs)):
V.append({})
newpath = {}
for y in states:
# 概率 隐状态 = 前状态是y0的概率 * y0转移到y的概率 * y表现为当前状态的概率。注:下面包含了一个列表生成式
(prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0)
for y0 in states])
V[t][y] = prob # 记录最大概率
newpath[y] = path[state] + [y] # 记录路径
print(V[t])
path = newpath # 不需要保留旧路径
print(path)
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
return prob, path[state]
if __name__ == '__main__':
states = ('Rainy', 'Sunny') # 隐状态
observations = ('walk', 'shop', 'clean') # 观测序列
start_probability = {'Rainy': 0.6, 'Sunny': 0.4} # 状态初始概率分布 π
# 状态转移矩阵 A
transition_probability = {
'Rainy': {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny': {'Rainy': 0.4, 'Sunny': 0.6},
}
# 观测概率矩阵 B(又称:发射概率矩阵、混淆矩阵)
emission_probability = {
'Rainy': {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
'Sunny': {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}
result = viterbi(observations,
states,
start_probability,
transition_probability,
emission_probability)
print(result)
运行结果:
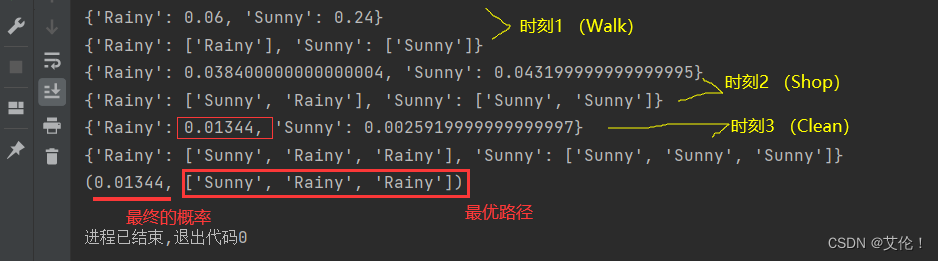
补充:下面是上述代码中涉及的部分 python 知识点梳理
- 在 viterbi 函数中,
(prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])包含了 python 的列表生成式- 含义:
# 概率 隐状态 = 前状态是y0的概率 * y0转移到y的概率 * y表现为当前状态的概率。 (prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states]) """ 代码解析:(结合完整代码进行理解) ① 列表生成式: [(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states] —— 循环获取 states 中的每个状态,计算概率,并分别以 (概率,前状态) 元组的形式呈现,然后用列表依次装着这些元组; ② max(...) 对列表中的元组取最大值,元组是逐位比较大小的: —— 将第一个元组的第一项与第二元组的第一项进行比较,若它们不相等(即第一个大于或小于第二个)那么这就是比较的结果。否则考虑第二项,然后是第三项,依此类推。 ③ 将最终得到的元组 如 (0.01344, 'Rainy') 中的元素值分别对应赋值给 prob、state ,即:prob=0.01344、state='Rainy'。 """ - 示例:列表生成式
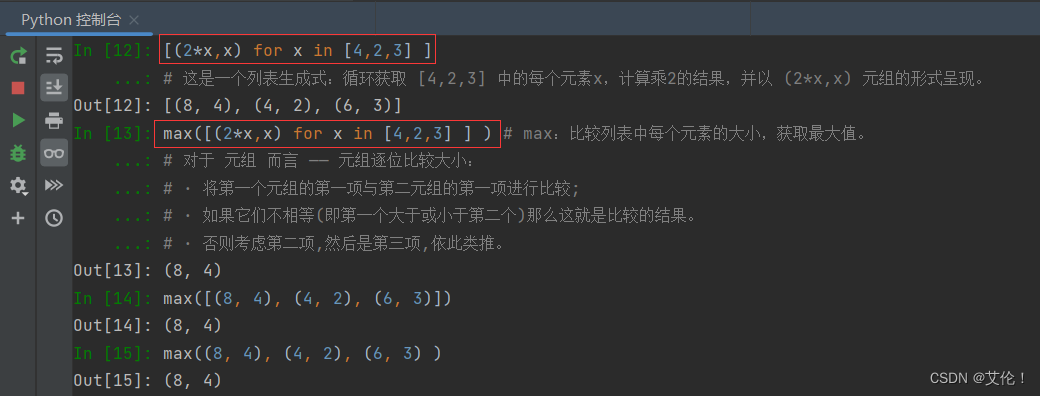
- 含义:
—— 说明:本文写于 2023.1.27~1.29,文中内容基于 python3,使用工具 PyCharm 编写的代码










![[MRCTF2020]PixelShooter1题解](https://img-blog.csdnimg.cn/img_convert/939e6917d299dd952ad519b7ea375bfe.jpeg)