目录
# 学习要求
前置知识
三维几何变换总的式子:
平移变换
比例变换
旋转变换:绕x轴旋转
反射变换
错切变换
三维复合变换
坐标系变换
正交投影矩阵
三视图
斜投影定义
透视投影
透视变换坐标系
## 代码
透视投影分类
# 学习要求
- 熟练掌握三维几何变换矩阵
- 掌握正交投影
- 掌握斜投影
- 熟练掌握透视投影
前置知识
三维变换同样引入了齐次坐标技术,在四维空间(x,y,z,w)内进行讨论。
定义了规范化齐次坐标以后,三维图形几何变换就可以表示为物体顶点集合的规范化齐次坐标矩阵与某一变换矩阵相乘的形式。(似曾相识呢)
用规范化齐次坐标表示的三维图形几何变换矩阵是一个4×4方阵,简称为三维几何变换矩阵。

基本上往下都是围绕三个坐标轴来展开计算了。
三维几何变换总的式子:
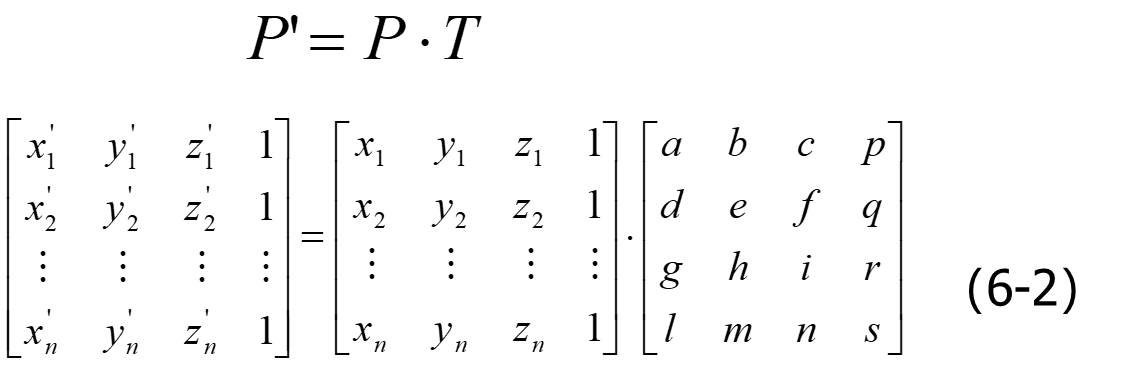
平移变换
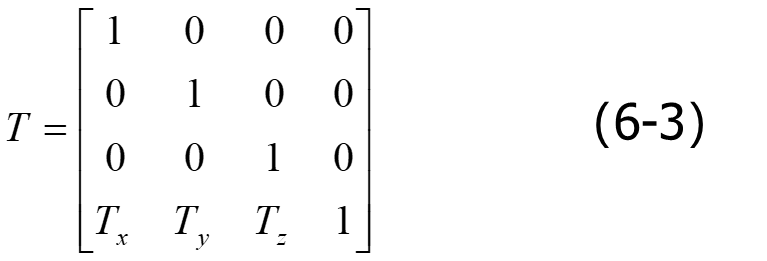
比例变换

旋转变换:绕x轴旋转


反射变换


好吧,没想到还有关于平面的反射。
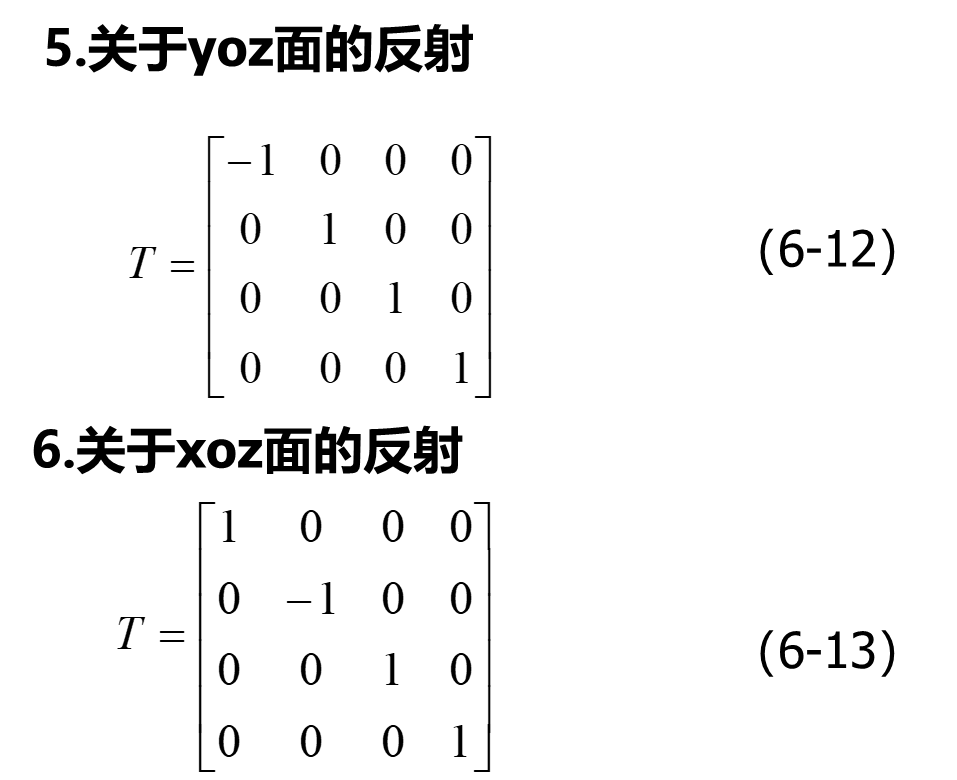
错切变换

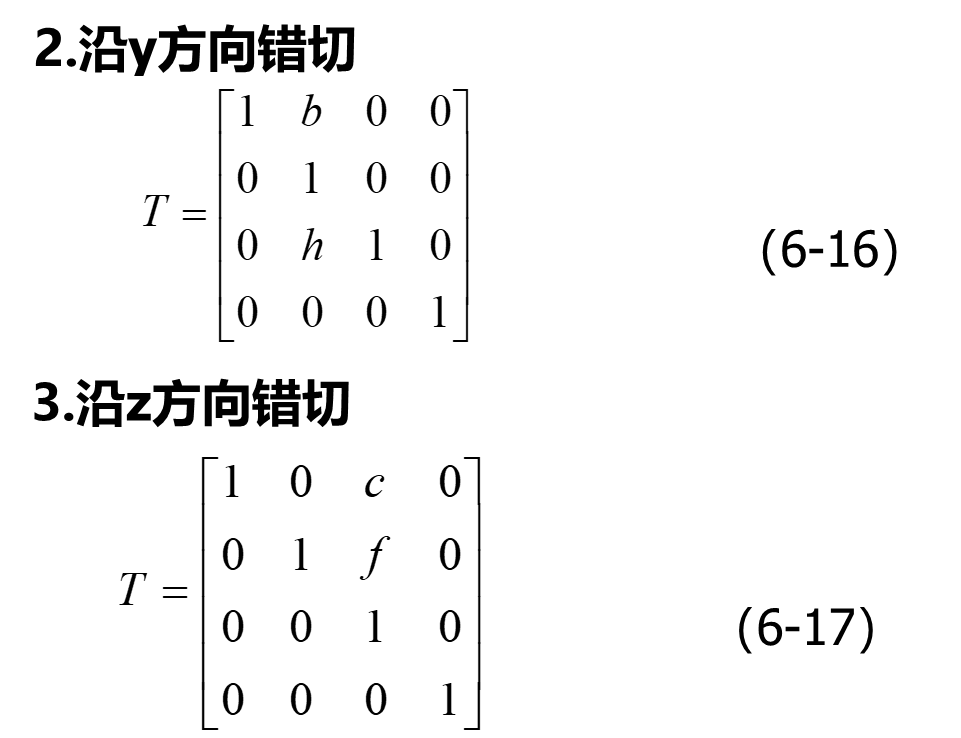
三维复合变换
总的式子
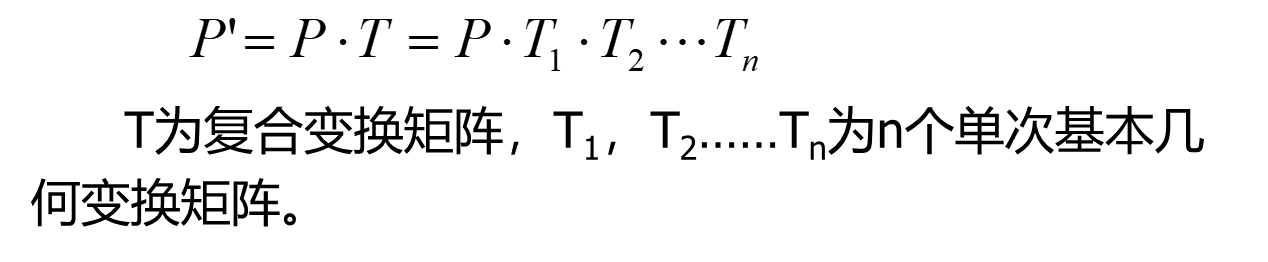
T的原式在上面。
在三维基本几何变换中,比例变换和旋转变换是与参考点相关的。
相对于任一参考点Q(x,y,z)的比例变换和旋转变换应表达为复合变换形式。
变换方法是(似曾相识)
- 首先将参考点平移到坐标原点,相对于坐标原点作比例变换或旋转变换,
- 然后再进行反平移将参考点平移回原位置。
相对于任意方向的变换方法是
- 首先对任意方向做旋转变换,使变换方向与某个坐标轴重合,
- 然后对该坐标轴进行三维基本几何变换,
- 最后做反向旋转变换,将任意方向还原到原来的方向。
三维几何变换中需要进行两次旋转变换,才能使任意方向与某个坐标轴重合。
- 一般做法是先将任意方向旋转到某个坐标平面内,然后再旋转到与该坐标平面内的某个坐标轴重合。


看清楚嗷,是谁绕谁旋转。






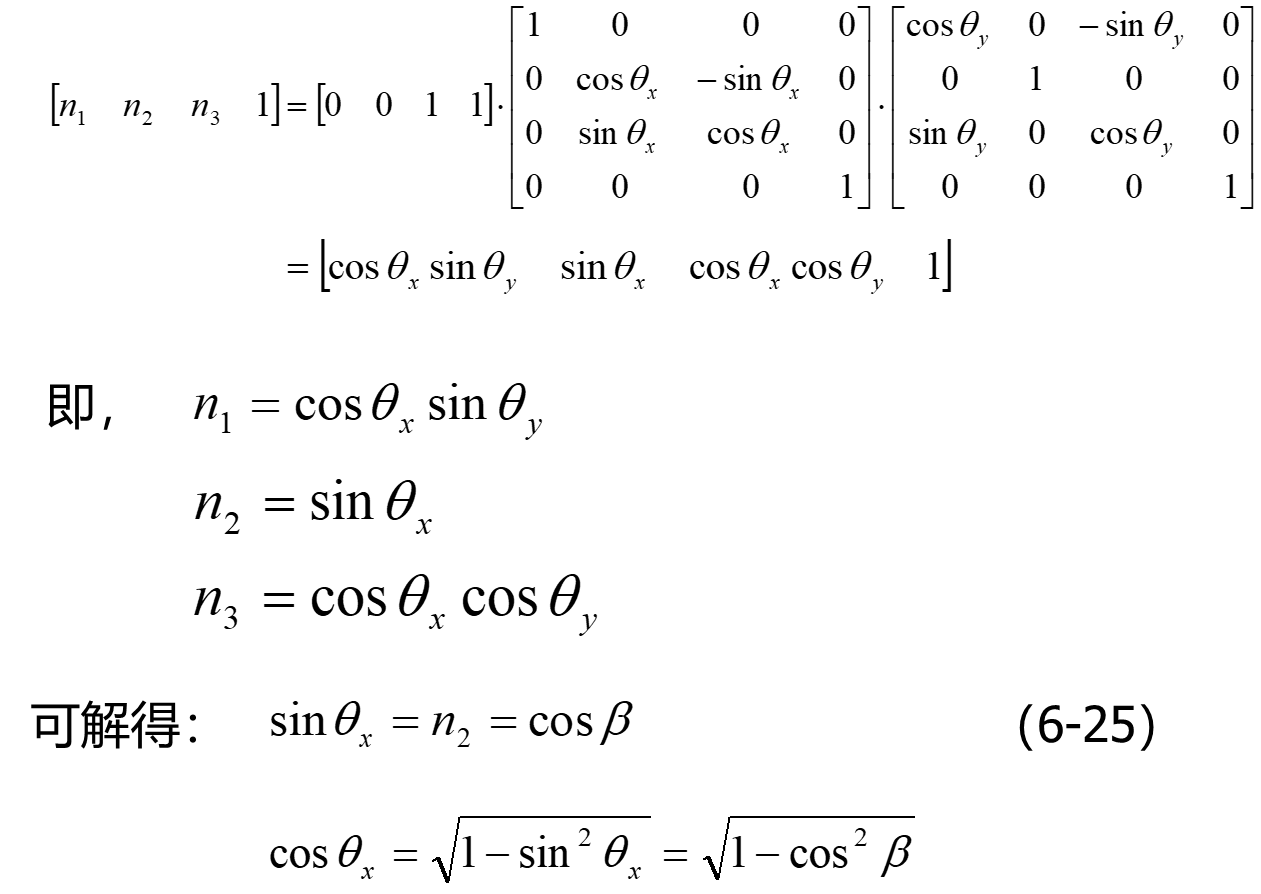

坐标系变换
在进行三维观察时,需要将物体的描述从世界坐标系变换到观察坐标系,然后通过旋转视点可以观察物体的全貌。
同一种变换既可以看作是点变换也可以看作是坐标系变换。点变换是顶点位置发生改变,但坐标系位置不发生改变。坐标系变换是建立新坐标系描述旧坐标系内的顶点,坐标系位置发生改变,但顶点位置不发生改变。


正交投影矩阵

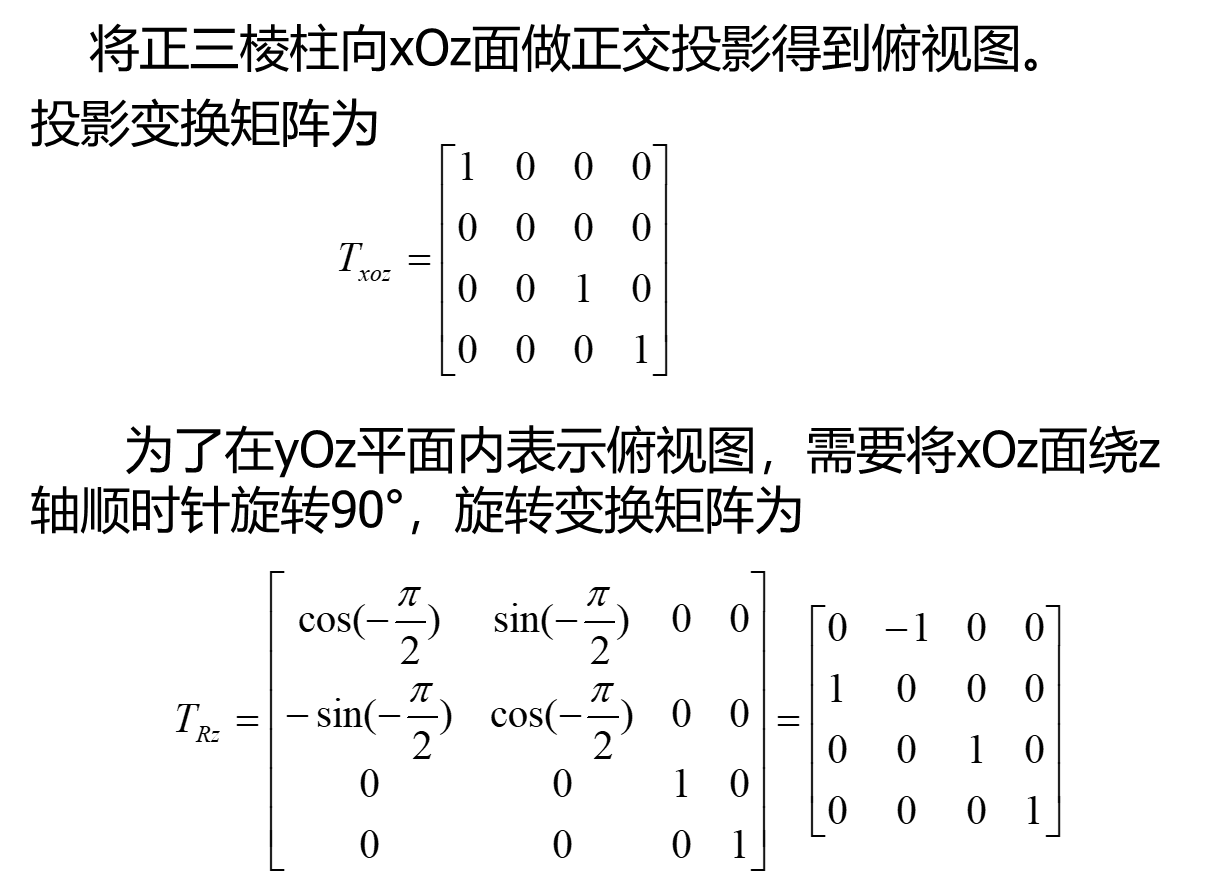
三视图
一个物体有6个视图:从物体的前面向后面投射所得的视图称主视图,从物体的上面向下面投射所得的视图称俯视图,从物体的左面向右面投射所得的视图称侧视图,还有其它三个视图不是很常用。
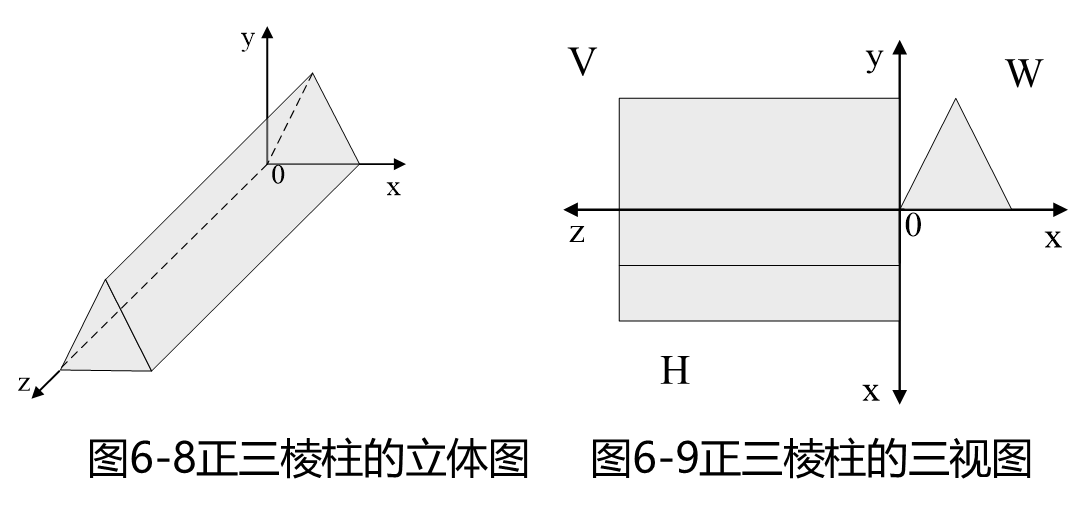
主视图

俯视图

侧视图


使用上述三视图变换矩阵绘制的三视图虽然位于都同一平面内,但却彼此相连。这对于使用不同的视区单独绘制主视图、俯视图和侧视图,不会产生影响。
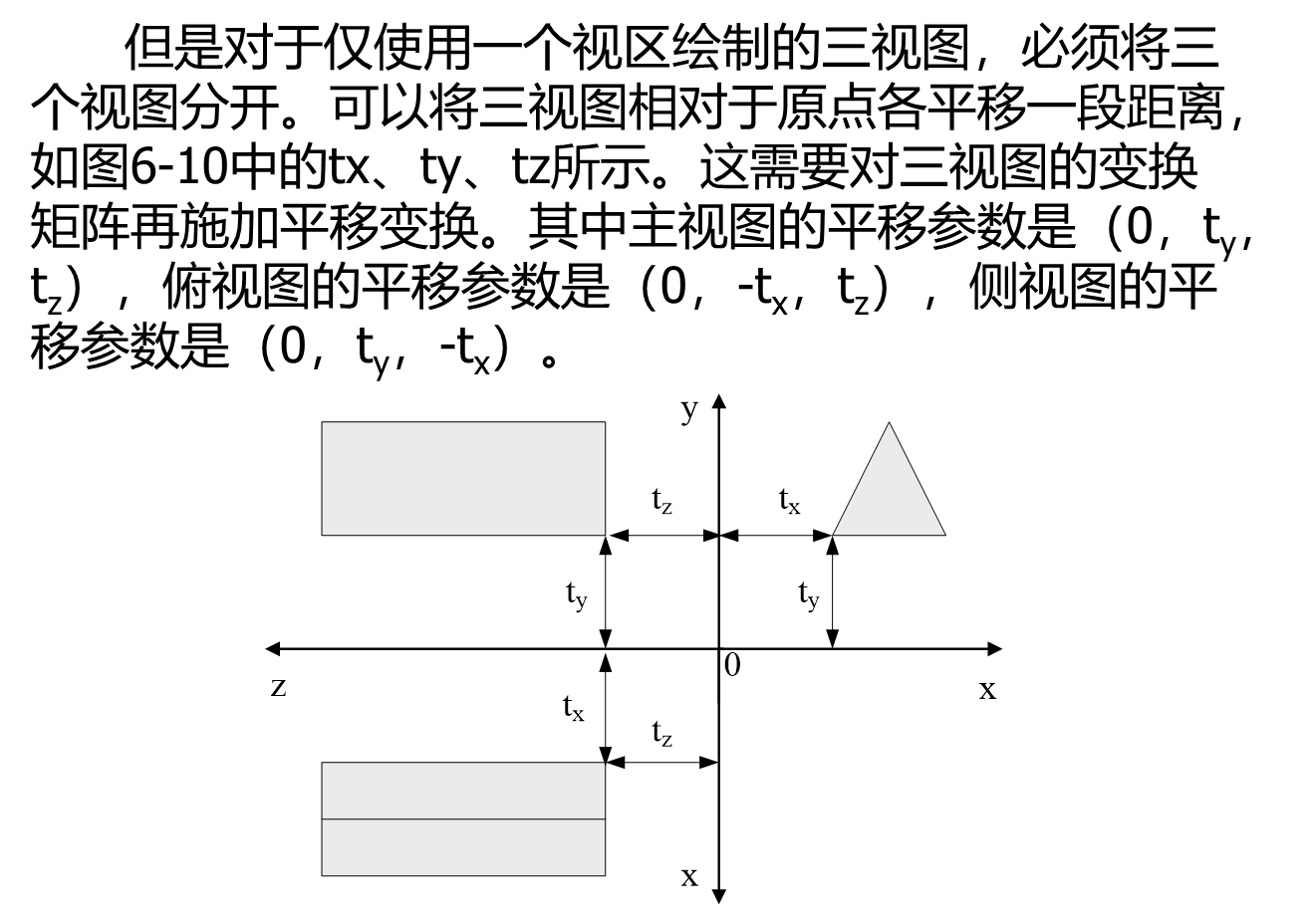


斜投影定义
将三维物体向投影面内作平行投影,但投影方向不垂直于投影面得到的投影称为斜投影。
与正交投影相比,斜投影具有较好的立体感。
斜投影也具有部分类似正交投影的可测量性,平行于投影面的物体表面的长度和角度投影后保持不变。


透视投影
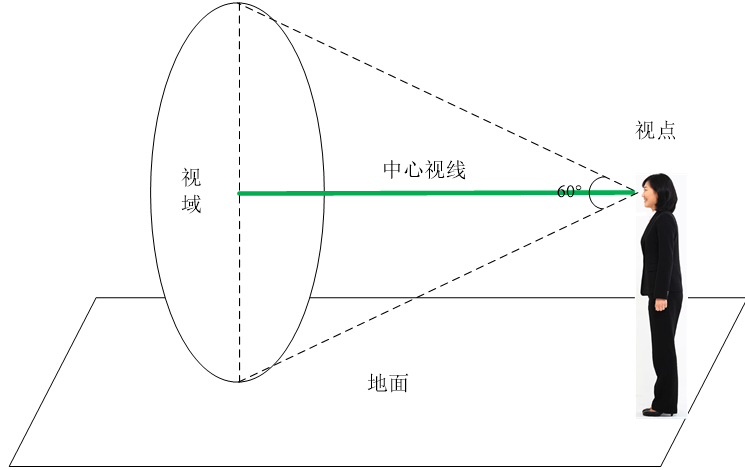
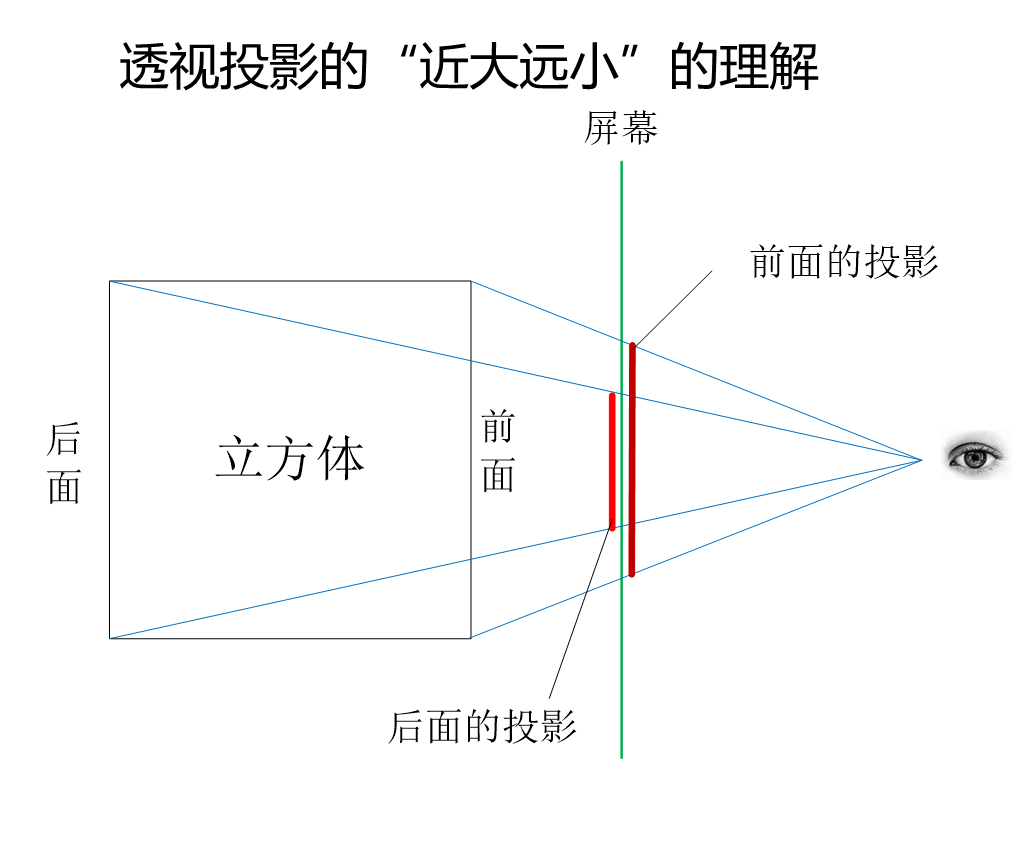
与平行投影相比,透视投影的特点是所有投影线都从空间一点(称为视点或投影中心)投射,
离视点近的物体投影大,离视点远的物体投影小,小到极点消失,称为灭点(vanishing point)。
一般将屏幕放在观察者和物体之间。投影线与屏幕的交点就是物体上一点的透视投影。
视点代表人眼或照相机、摄像机的位置,是观察坐标系的原点。视心是屏幕坐标系的原点。

透视变换坐标系











## 代码
void CTestView::InitParameter()
{
//初始化三角函数
k[1]=sin(PI*Theta/180);
k[2]=sin(PI*Phi/180);
k[3]=cos(PI*Theta/180);
k[4]=cos(PI*Phi/180);
k[5]=k[2]*k[3];
k[6]=k[2]*k[1];
k[7]=k[4]*k[3];
k[8]=k[4]*k[1];
//世界坐标系的视点球坐标
ViewPoint.x=R*k[6];
ViewPoint.y=R*k[4];
ViewPoint.z=R*k[5];
}

编程实现将物体的坐标描述从世界坐标系转换到
观察坐标系,函数WorldToView() :
void CTestView::WorldToView(CP3 WorldP)
{
CP3 ViewP;
ViewP.x=k[3]* WorldP.x-k[1]* WorldP.z;
ViewP.y=-k[8]* WorldP.x+k[2]* WorldP.y-k[7]* WorldP.z;
ViewP.z=-k[6]* WorldP.x-k[4]* WorldP.y-k[5]* WorldP.z+R;
}
WorldP为观察坐标系三维点,ViewP为观察坐标系的三维点。本段代码完成了将世界坐标系中一点的坐标表示转换到观察坐标系中表示。




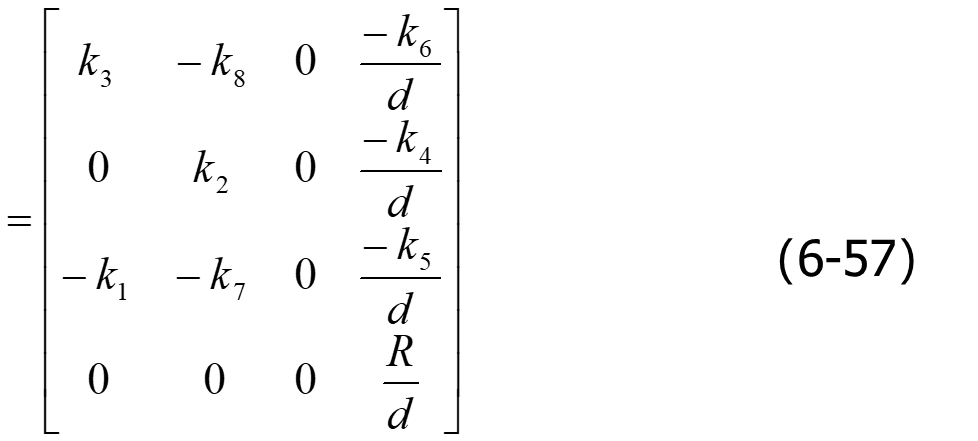
CP2 CTestView::PerProject(CP3 ViewP)
{
CP2 ScreenP;// ScreenP屏幕坐标系二维点
ScreenP.x=d*ViewP.x/ViewP.z;
ScreenP.y=Round(d*ViewP.y/ViewP.z);
return ScreenP;
}
本段代码将观察坐标系中的三维点ViewP透视投影
转换为屏幕坐标系中的二维点ScreenP。
透视投影分类
透视投影中,与屏幕平行的平行线投影后仍保持平行。
不与屏幕平行的平行线投影后汇聚为灭点,灭点是无限远点在屏幕上的投影。
每一组平行线都有其不同的灭点。坐标轴上灭点称为主灭点。
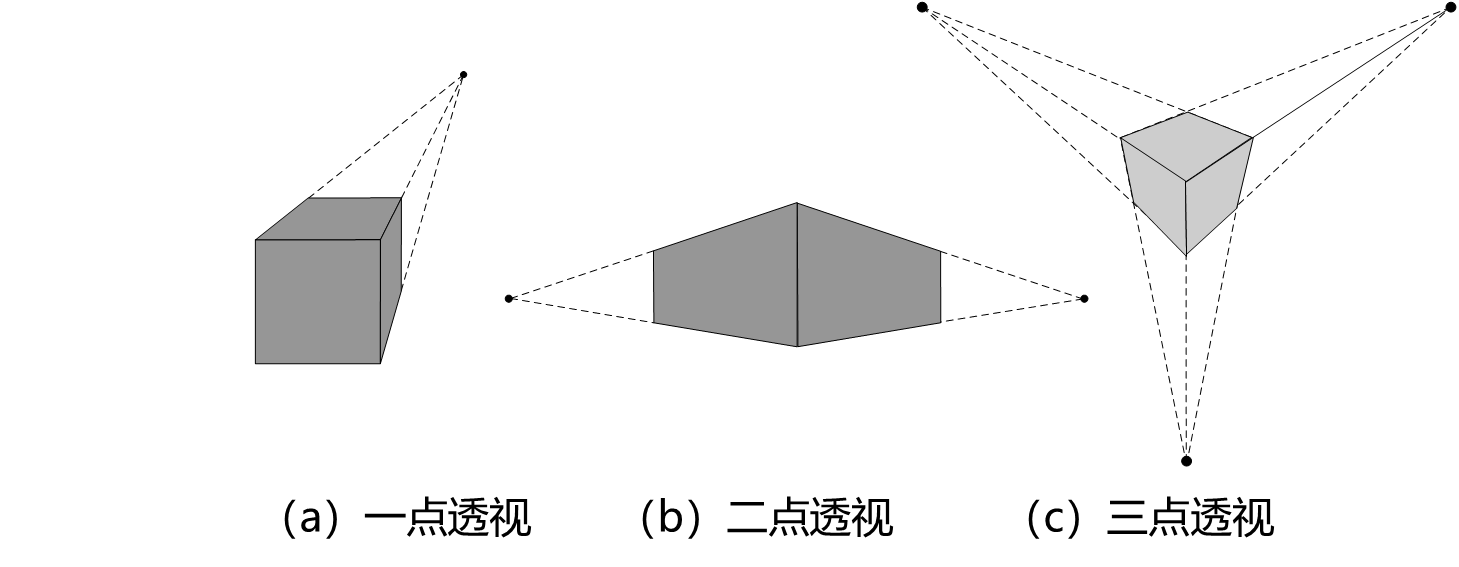
透视投影中主灭点数目是由屏幕切割坐标轴的数量来决定,并据此将透视投影分类为一点、二点和三点透视。
一点透视有一个主灭点,即屏幕仅与一个坐标轴正交,与另外两个坐标轴平行;
二点透视有两个主灭点,即屏幕仅与两个坐标轴相交,与另一个坐标轴平行;
三点透视有三个主灭点,即屏幕与三个坐标轴都相交


物体是三维坐标系,屏幕是二维坐标系。投影就是将三维转换为二维,也就是处理掉z坐标。
观察坐标系的三维坐标转换为屏幕坐标系的二维坐标的方法有以下几种:




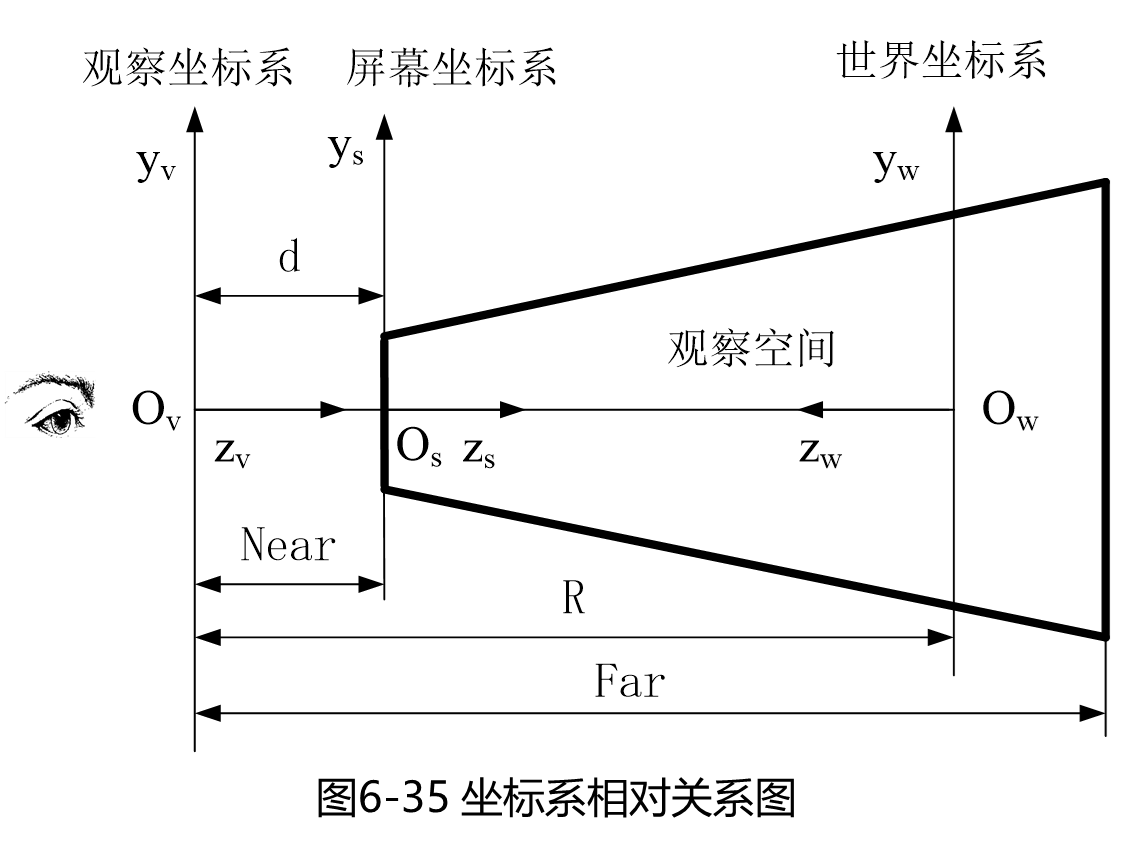
式中,Near和Far是常数,且Near就是视距d。透视变换的一个重要性质是把直线映射为直线,平面映射为平面。


![[MRCTF2020]PixelShooter1题解](https://img-blog.csdnimg.cn/img_convert/939e6917d299dd952ad519b7ea375bfe.jpeg)