NetworkX官方基础教程:图的生成与相关操作
- 1. Graph生成和graph操作
- 2. 分析图
- 3. 画图
- 参考资料
本文作为对图结构和复杂网络的快速上手,内容包括基于NetworkX进行图的生成与相关操作,Graph的分析以及绘制Graphs。
NetworkX官方基础教程
1. Graph生成和graph操作
可以指定使用一个nbunch报告所有节点的子集的边和度。nbunch是以下任何一种:None(表示所有节点)、节点或本身不是图中节点的节点的一个可迭代容器。
除了逐节点或逐边构造图之外,它们还可以通过以下方法生成:
-
应用经典的graph操作,例如:
- subgraph(G, nbunch) : 返回在nbunch中的节点上导出的子图
- union(G, H[, rename]) :组合图G和图H
- disjoint_union(G, H) :组合图G和图H
- cartesian_product(G, H) :返回图G和图H的笛卡儿积
- compose(G, H) :通过将节点和边组合成一个单一的图来组合图G和图H
- complement(G) :返回图G的补图
- create_empty_copy(G[, with_data]) :返回图G的一个副本,其中移除了所有的边
- to_undirected(graph) :返回图graph的无向视图
- to_directed(graph) :返回图graph的有向视图
-
使用对典型的小尺度图的调用,例如:
- petersen_graph([create_using]) :返回 Petersen 图。
- tutte_graph([create_using]) : 返回 Tutte 图。
- sedgewick_maze_graph([create_using]) :用一个循环返回一个小maze图。
- tetrahedral_graph([create_using]) :返回3-正则柏拉图四面体图
-
为经典图使用一个(构造性的)生成器,例如:
- complete_graph(n[, create_using]) : 返回具有 n 个节点的完整图
K_n - complete_bipartite_graph(n1, n2[, create_using]) : 返回完全二分图
K_{n_1,n_2}。 - barbell_graph(m1, m2[, create_using]) : 返回杠铃图: 两个完整的图由一个路径连接。
- lollipop_graph(m, n[, create_using]) : 返回棒棒糖图; K_m连接到P_n。
- complete_graph(n[, create_using]) : 返回具有 n 个节点的完整图
例如:
import networkx as nx
from networkx.generators.classic import lollipop_graph
K_5 = nx.complete_graph(5)
K_3_5 = nx.complete_bipartite_graph(3, 5)
barbell = nx.barbell_graph(10, 10)
lollipop = nx.lollipop_graph(10, 20)
- 使用随机图生成器, 例如
- erdos_renyi_graph(n, p[, seed, directed]) : 返回一个 G n , P G_{n,P} Gn,P随机图,也称为Erdős-Rényi图或二项图。
- watts_strogatz_graph(n, k, p[, seed]) :返回 Watts-Strogatz 小世界图。
- barabasi_albert_graph(n, m[, seed, …]) : 使用 Barabási-Albert 优先附件返回一个随机图
- random_lobster(n, p1, p2[, seed]) : 返回一个随机龙虾图。
例如:
er = nx.erdos_renyi_graph(100, 0.15)
ws = nx.watts_strogatz_graph(30, 3, 0.1)
ba = nx.barabasi_albert_graph(100, 5)
red = nx.random_lobster(100, 0.9, 0.9)
- 使用通用图形格式读取存储在文件中的图形
NetworkX 支持许多流行的格式,例如边列表、邻接列表、 GML、 GraphML、 LEDA 等。
nx.write_gml(red, "path.to.file")
mygraph = nx.read_gml("path.to.file")
2. 分析图
图G的结构可以用各种图论函数来分析,例如:
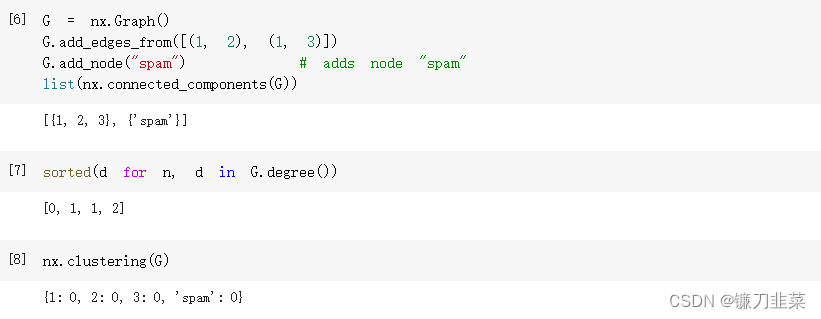
一些具有大输出的函数遍历(节点,值)2-元组。如果需要,可以很容易地将它们存储在 dict 结构中。

3. 画图
NetworkX 主要不是一个图形绘制软件包,而是基于Matplotlib的基本绘制,以及一个使用开源 Graphviz 软件包的界面。这些都是 networkx.uring模块的一部分,如果可能的话将导入它们。
首先导入 Matplotlib 的 plot 接口(pylab 也可以工作):
import matplotlib.pyplot as plt
为了测试导入 nx_ pylab 是否成功,使用:
当绘制到交互式显示时。请注意,可能需要发出Matplotlib
plt.show()
如果在交互模式下不使用matplotlib,则使用。
options = {
'node_color': 'black',
'node_size': 100,
'width': 3,
}
subax1 = plt.subplot(221)
nx.draw_random(G, **options)
subax2 = plt.subplot(222)
nx.draw_circular(G, **options)
subax3 = plt.subplot(223)
nx.draw_spectral(G, **options)
subax4 = plt.subplot(224)
nx.draw_shell(G, nlist=[range(5,10), range(5)], **options)
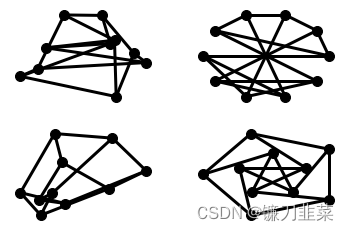
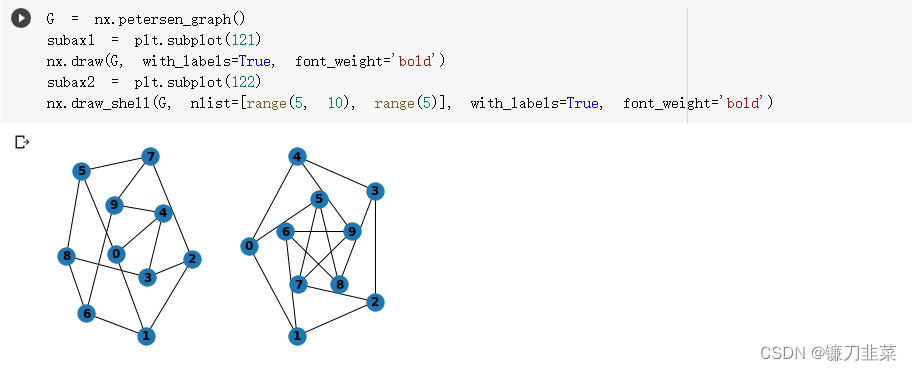
可以通过draw_networkx()找到其他选项,通过布局模块找到布局。 可以将多个shells与draw_shell() 一起使用。
G = nx.dodecahedral_graph()
shells = [[2, 3, 4, 5, 6], [8, 1, 0, 19, 18, 17, 16, 15, 14, 7], [9, 10, 11, 12, 13]]
nx.draw_shell(G, nlist=shells, **options)
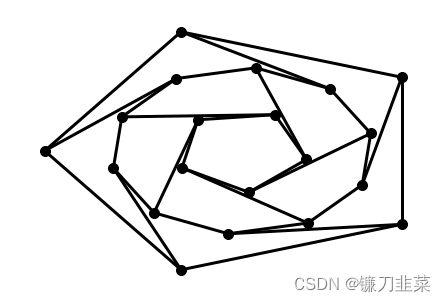
若要将绘图保存到文件中,请使用:
nx.draw(G)
plt.savefig("path.png")
此函数写入本地目录中的文件 path.png。 如果 Graphviz 和 PyGraphviz 或 pydot 可用,还可以使用 networkx.drawing.nx_agraph.graphviz_layout 或 networkx.drawing.nx_pydot.graphviz_layout 来获取节点位置,或以dot格式编写图以进行进一步处理。
from networkx.drawing.nx_pydot import write_dot
pos = nx.nx_agraph.graphviz_layout(G)
nx.draw(G, pos=pos)
write_dot(G, 'file.dot')
参考资料
[1] NetworkX Tutorial
[2] https://networkx.org/documentation/stable/reference/introduction.html








![[MRCTF2020]PixelShooter1题解](https://img-blog.csdnimg.cn/img_convert/939e6917d299dd952ad519b7ea375bfe.jpeg)