一、前言
要素的属性及位置是 GIS数据的固有信息。此信息将用于创建视觉上可 进行分析的地图。统计分析有助于从 GIS 数据中提取只靠查看地图无法直接 获得的额外信息,例如各属性值如何分配,数据中是否存在空间趋势或者要素 是否能够形成空间模式。因此,对数据进行探索性空间数据分析能更深入了解 数据,认识研究对象,从而有利于更好地对数据进行空间建模与分析,做出更好的决策。
二、探索性空间数据分析方法
19 世纪60 年代的 Tukey 面向数据分析的主题,提出了探索性数据分析 (EDA,Exploratory Data Analysis)的新思路,解决了传统统计分析中数据不能满 足正态假设,基于均值、方差的模型在实际数据分析中缺乏稳定性的问题,并且 满足了对海量数据进行分析的要求。EDA 的特点是对数据来源的总体不作假 设,并且假设检验也经常被排除在外。这一技术使用统计图表、图形和统计概 况的方法对数据的特征进行分析和描述,技术核心是“让数据说话”,在探索的 基础上对数据进行更为复杂的建模分析(王远飞,何洪林,2007)。在EDA的基 础上衍生出的是探索性空间数据分析(ESDA,Exploratory Spatial Data Analysis),是EDA在空间数据分析领域的推广。 在进行区域经济空间分析与建模之前,应该使用 ESDA 工具浏览数据。此 工具能使我们更深入地了解数据的分布、寻找离群值、进行全局趋势分析以及检测空间的自相关和方向变异等任务,并为空间分析与建模选择最合适的方法 和参数。例如,在进行回归分析之前,应该事先检查数据的分布,是否有异常 值,是否具有空间趋势,是否符合正态分布等等。ESDA 环境允许用户用图形 的方法研究数据集,从而能更好地理解所要研究的数据集。每个 ESDA工具都 对该数据给出一个不同的视图并在单独的窗口中显示出来。这些不同的视图 包括直方图、Voronoi 地图、正态 QQ 图、趋势分析、半变异/协方差函数云等。
(一)单数据集方法
(1)直方图
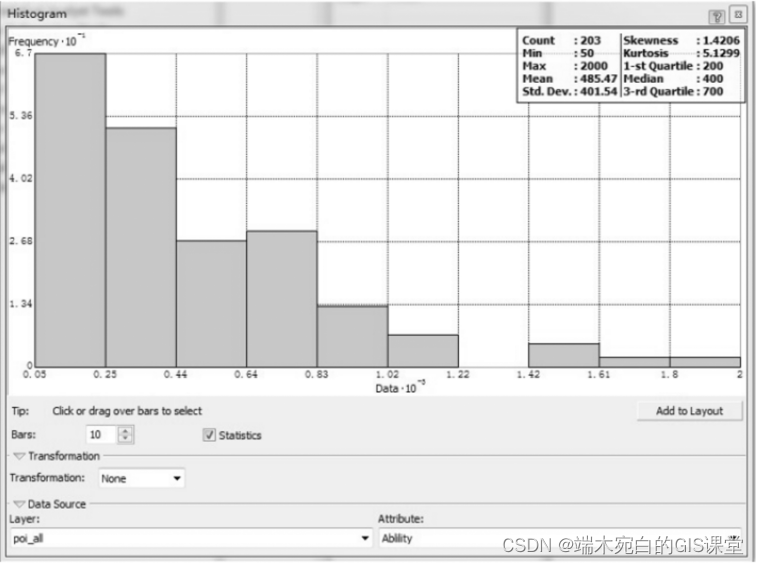
直方图可以用于观察数据集的总体分布并用于汇总相关的统计数据,比如 最大最小值、平均值、标准差、中位数等。如下图所示,可以看出,该属性并不呈 现出典型的正态分布,并且在右上角的图例中可以看到一系列常规的统计指 标,用于参考。
(2) Voronoi图
Voronoi 图,也称泰森多边形,考虑每个多边形内有一个样点,多变形内任 一点到该点的距离都小于其他多边形到该点的距离,从而生成多边形。通过 Voronoi 地图可以直观地观测数据集的空间可变性和稳定性,图中每个点对应 的Voronoi 多边形的面积的倒数可以作为一个评价点局部密度的指标,判断点 集的分布属于哪一种形式(随机分布或者集聚、规则分布)。还可以根据其中 一个多边形与相邻多边形的差异情况来识别研究对象中的异常值。

(3)正态QQ图
该统计量用于评估所研究的数据集是否表现为正态分布。简单来说,即是 使用研究的对象数据集与正态分布的标准数据集对比得出差异,用于观测数据 集的相关特征。如下图所示,数据集与正态分布线相对接近,具有一定的正态分布特征。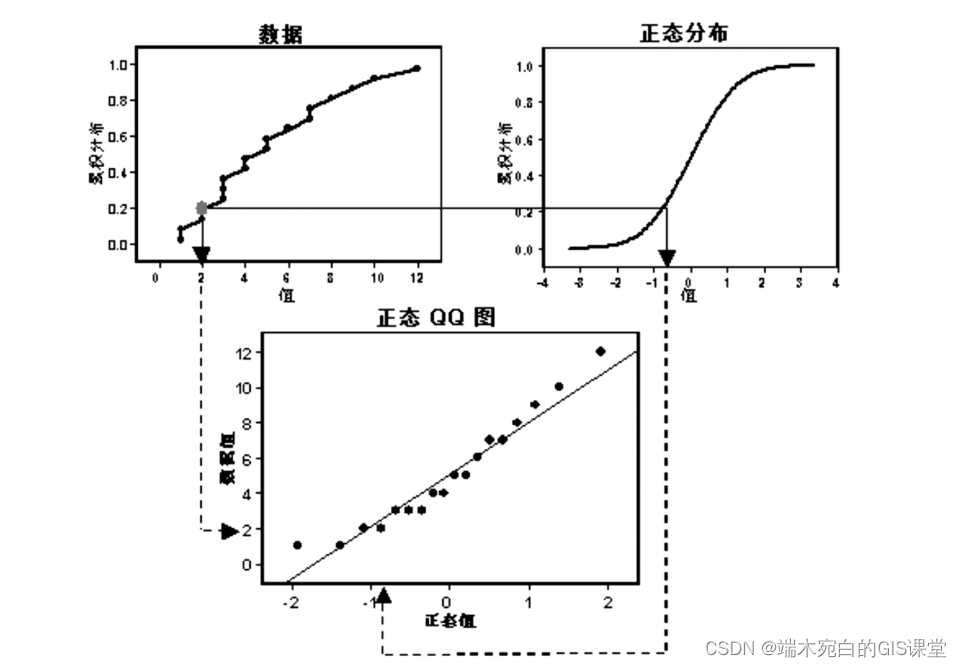
(4)趋势分析
用于查看和检查数据集中的空间趋势。样点的位置可以在X、Y 平面上来 表示,对于感兴趣的属性值,则可通过垂直方向上的 Z轴来表示,构成三维视图 。在进行趋势分析时,将Z 轴数据值分别投影到X、Z平面和 Y、Z平面作散点图,这也可以被看作是三维数据的侧视图,然后用多项式来拟 合投影平面上的散点图。如果经过投影后的曲线是平直的,表明没有趋势;如 果多项式有确定的形式,如是呈上升趋势的曲线模式,则表明数据中存在全局 趋势。通常 X 轴代表东西方向,Y 轴代表南北方向,如果方向呈水平,则无趋 势。反之,则存在趋势。图中可见南北方向,东西方向均存在趋势。
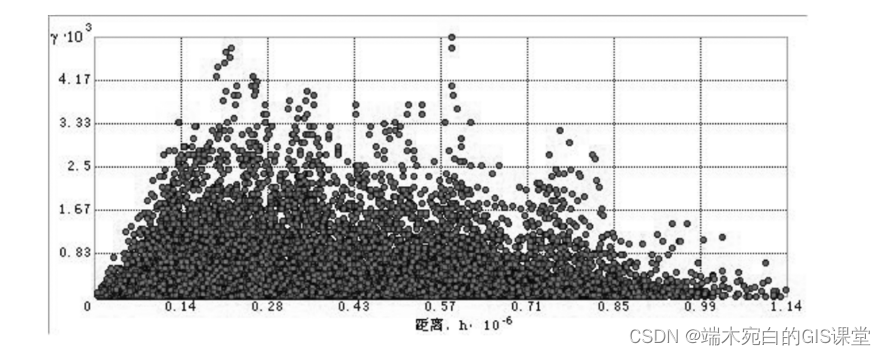
(5) 半变异/协方差函数云
半变异/协方差函数表示的是数据集中所有样点对的理论半变异值和协方 差,把它们用两点间距离的函数来表示,并以此函数作图,称半变异/协方差函数云图,图表的横坐标表示任两点的空间距离,纵标表示该两点的 半变异函数值。引入半变异/协方差函数云图的目的是探索和量化空间相关性,也叫做空间自相关。空间自相关量化的假设条件是距离相近的事物比距离 远的事物具有更大的相似性,那些距离较远的样点对将具有更大的相异性和较 高的方差,因而 x值越小,y值应该越小。
(二)双数据集方法
以上介绍的几种方法,每次可以用于分析一个数据集的探索性空间属性, 接下来的两种方法可以对两个数据集之间的关系进行初步的探索。
(1)常规 QQ 图 常规 QQ 图用于评估两个数据集之间分布的相似程度,与前面的正态 QQQ 图的绘制类似,不同之处在于,正态 QQ 图是利用目标数据集与正态分布相对 比得出,而常规 QQ 图的对比数据集是另一目标数据集,如果两个数据集具有 相同的分布,那么分布曲线将与 45 度对角线重合。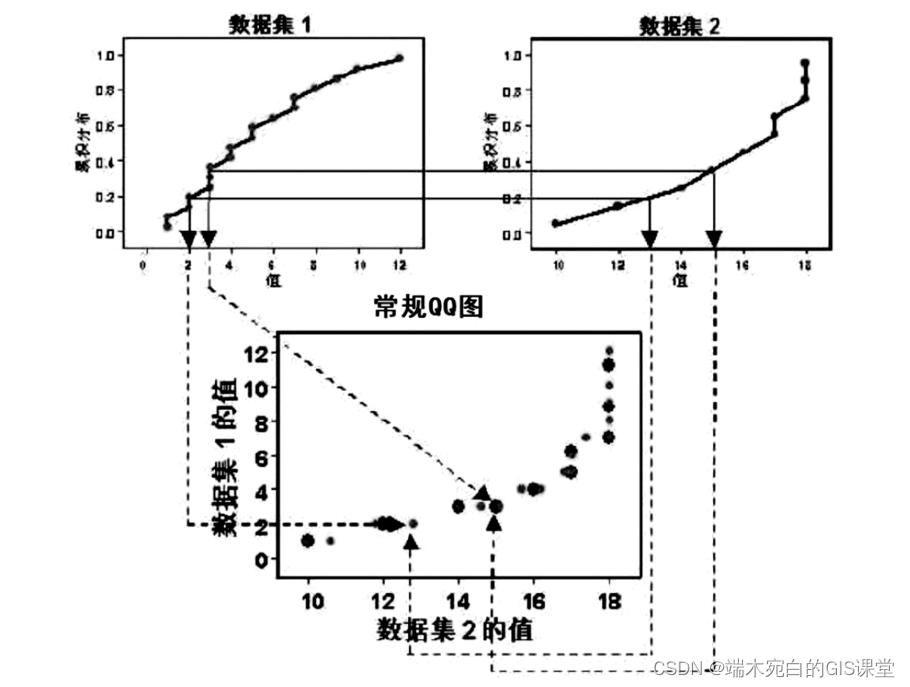
(2) 交叉协方差云
交叉协方差云显示了两个数据集之间所有位置对的经验交叉协方差,并且将其作为两位置间距离的函数对其进行绘图。交叉协方差云可以用来检查两 个数据集之间空间相关的局部特征,并且能够用于在两个数据集之间的相关中 查找空间平移,交叉协方差云图如图所示。使用交叉协方差云工具检查协 方差表面是否对称以及交叉协方差值在各个方向上是否类似。如果发现在隔 离的位置或研究地点的受限区域内存在异常的交叉协方差值,则需要采取一些 操作,如去除数据趋势或者在对数据进行插值之前将数据分割为不同的图层。