由于顺序表（数组）的插入、删除操作需要移动大量的元素，影响了运行效率，因此引入了线性表的链式存储——单链表。单链表通过一组任意的存储单元来存储线性表中的数据元素，不需要使用地址连续的存储单元，因此它不要求在逻辑上相邻的两个元素在物理位置上也相邻，所以单链表是非随机存取结构，不能直接找到表中某个特定的结点。查找某个特定的结点时，需要从第一个结点开始遍历，依次查找。

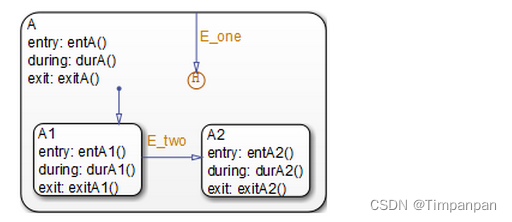
单链表的基本构成

其中：data表示数据域，用于存放该结点的数据信息；next表示指针域，用于存放相邻下一结点的地址。

单链表中结点类型的描述如下：
struct LNode {
	int data;
	LNode* next;
};

单链表的基本操作

单链表的查找-按值进行查找

查找值x在单链表L中的结点指针（指针即地址）。

算法思想：从单链表的第一个结点开始，依次比较表中各个结点的数据域的值，若某结点数据域的值等于num，则返回该结点的指针；若整个单链表中没有这样的结点，则返回空。

按值查找结点值的算法如下：
LNode *LocateElem(LNode *L, int num) {
	LNode *p = L->next;
	while (p != NULL && p->data != num) {
		p = p->next;
	}
	return p;
}

单链表的查找-按位置进行查找

查找单链表L中第 i（i>0）个位置的结点指针。

算法思想：从单链表的第一个结点开始，顺着指针域逐个往下搜索，直到找到第 i 个结点为止，否则返回最后一个结点的指针域NULL。

按位查找结点值的算法如下：
LNode *GetElem(LNode *L, int i) {
	LNode *p = L->next;
	if (p == NULL) {
		return NULL;
	}
	int j = 1;
	while (p != NULL && j < i) {
		p = p->next;
		j++;
	}
	return p;
}

单链表的建立-头插法

所谓头插法建立单链表就是将新结点插入到当前链表的表头，即头结点之后。如图所示：

算法思想：首先初始化一个单链表，其头结点为空，然后循环插入新结点*p：将p的next指向头结点的下一个结点，然后将头结点的next指向p。

主要代码：
LNode *p = new LNode; //申请新结点p
p->data = x; //给新结点赋值，x是已知值
p->next = L->next; //将原头结点的next指针域值赋值给新结点next指针域
L->next = p; //将头结点连接到新结点

头插法建立单链表的算法如下：
LNode *HeadInsert() {
	LNode *L = new LNode;  //创建头结点
	L->next = NULL;  //初始时使头结点指向空
	int x;
	while (cin >> x) {
		LNode *p = new LNode;
		p->data = x;
		p->next = L->next;
		L->next = p;
	}
	return L;
}

需要指出的是，头插法建立的单链表中结点的次序和输入数据的顺序不一致，是相反的。若希望两者的顺序是一致的，则可采用尾插法建立单链表。

单链表的建立-尾插法

所谓尾插法建立单链表，就是将新结点插入到当前链表的表尾。如下图所示：

算法思想：首先初始化一个单链表，然后声明一个尾指针r，让r始终指向当前链表的尾结点，向单链表的尾部插入新的结点*p，将尾指针r的next域指向新结点，再修改尾指针r指向新结点，也就是当前链表的尾结点。最后别忘记插入所有结点之后，将尾结点的指针域置空。

主要代码：
LNode *p = new LNode; //申请新结点p
p->data = x; //给新结点赋值，x是已知值
r->next = p; //在原尾指针所指结点后插入新结点p
r = p; //插入新结点p后，更新尾指针的位置

尾插法建立单链表的算法如下：
LNode *TailInsert() {
	LNode *L = new LNode;
	L->next = NULL;
	int x;
	LNode *r = L;
	while (cin >> x) {
		LNode *p = new LNode;
		p->data = x;
		r->next = p;
		r = p;
	}
	r->next = NULL;
	return L;
}

单链表的插入

情况1：已知相邻结点中的一个（并且是插入后结点的前驱结点X）

插入步骤：
1.申请新结点p
2.给新结点p赋值
3.将原X结点的next域值赋值给新结点p的next域
4.将X结点连接到p，即将p赋值给X结点的next域

主要代码：
LNode *p = new LNode; //申请新结点p
p->data = x; //给新结点赋值，x是已知值
p->next = X->next; //将原X结点的next域值赋值给新结点p的next域
X->next = p; //X结点连接到p，即将p赋值给X结点的next域

情况2：已知两个相邻结点（前驱结点X，后继结点Y）

插入步骤：
1.申请新结点p
2.给新结点p赋值
3.将X结点连接到p，即将p赋值给X结点的next域
4.将p结点连接到Y，即将Y赋值给p结点的next域

主要代码：
LNode *p = new LNode; //申请新结点p
p->data = x; //给新结点赋值，x是已知值
X->next = p; //将X结点连接到p，即将p赋值给X结点的next域
p->next = Y; //将p结点连接到Y，即将Y赋值给p结点的next域

单链表的删除

将单链表的第 i 个结点删除。

算法思想：先检查删除位置的合法性，然后从头开始遍历，找到表中的第 i-1 个结点，即被删除结点的前驱结点p，被删除结点为q，修改p的指针域，将其指向q的下一个结点，最后再释放结点q的存储空间。

删除步骤：
1.将p结点指向原q结点的后驱，即将q结点的next域值赋值给p结点的next域
2.删除q结点，即调用free函数

主要代码：
从头开始遍历，找到表中的第 i-1 个结点（代码过程省略）
q->next = p->next; //将q结点的next域值赋值给p结点的next域
free(q); //删除q结点

后续更新《一章了解栈和队列》，各位看官，关注不迷路！！！