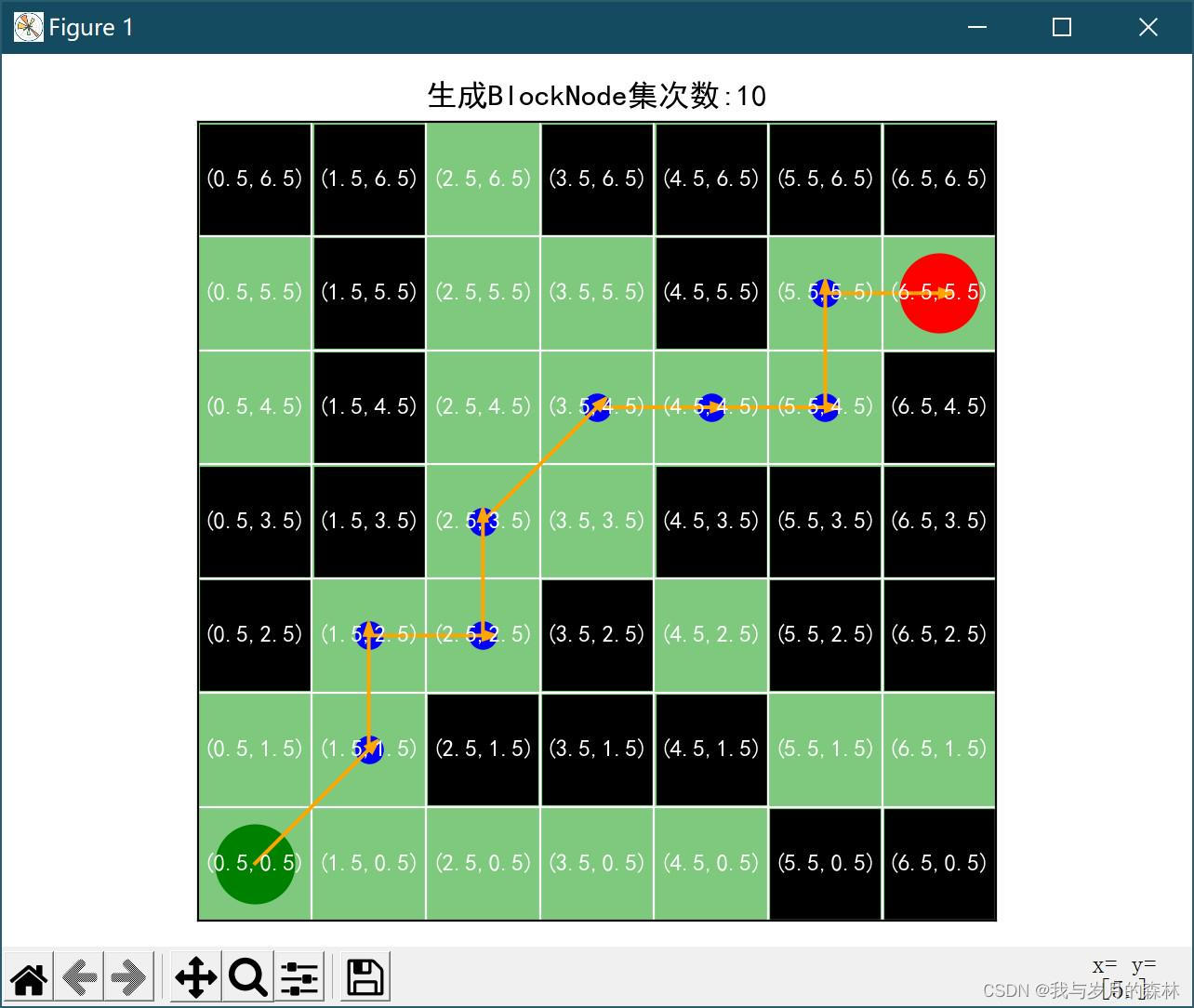
最近公共祖先（Lowest Common Ancestor，LCA）
指两个点的公共祖先中，离根最远/深度最深的

性质：
1. L C A ( { u } ) = u LCA\left(\left\{u\right\}\right) = u LCA({u})=u
2.若$u$是$v$的祖先，当且仅当$LCA\left(u,v\right)=u$
3.如果$u$不是$v$的祖先，$v$不是$u$的祖先，则$u,v$分别处于$LCA\left(u,v\right)$的两棵不同的子树中
4.两个点的LCA必定出现在两点间的最短路上
5.设$d\left(u,v\right)$为$u,v$之间的距离，$h\left(u\right)$为$u$到根的距离，则$d\left(u,v\right)=h\left(u\right)+h\left(v\right)-2h\left(LCA\left(u,v\right)\right)$

洛谷P3379

朴素

一步步往上跳

倍增

${\mathrm{fa}}_{x,i}$表示$x$的$2^i$个祖先，用dfs预处理
查询$x,y$的LCA时，先跳到同一个深度
然后按2的幂次从大到小跳，比如$5=101b$先跳$2^2$,再跳$2^0$
不过这么跳可能会跳过了，所以我们跳到LCA的子节点

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;

const int N = 500005;
const int M = 21;
vector<int> edge[N];

int logn[N] = { -1, 0 };//log2 n

int fa[N][M];//fa[i][j]表示i的2^j祖先
int depth[N];//深度

void dfs(int now, int father) {
	fa[now][0] = father;
	depth[now] = depth[father] + 1;
	for (int i = 1; i <= logn[depth[now]]; ++i){
		fa[now][i] = fa[fa[now][i - 1]][i - 1];
	}
	for (int i = 0; i < edge[now].size(); ++i) {
		if (edge[now][i] != father) {
			dfs(edge[now][i], now);
		}
	}
}

int lca(int x, int y) {
	if (depth[x] < depth[y])swap(x, y);
	//跳同一个深度
	while (depth[x] > depth[y]) {
		x = fa[x][logn[depth[x] - depth[y]]];
	}
	if (x == y)return x;
	//跳到LCA的子节点
	for (int i = logn[depth[x]]; i >= 0; --i) {
		if (fa[x][i] != fa[y][i]) {
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}


int main() {
	int n, m, s, x, y;
	scanf("%d%d%d", &n, &m, &s);
	for (int i = 1; i < n; ++i) {
		scanf("%d%d", &x, &y);
		//双向边，以为不知道哪个在上面
		edge[x].push_back(y);
		edge[y].push_back(x);
	}
	for (int i = 2; i <= n; ++i)logn[i] = logn[i >> 1] + 1;
	dfs(s, 0);
	while (m--) {
		scanf("%d%d", &x, &y);
		printf("%d\n", lca(x, y));
	}
	return 0;
}

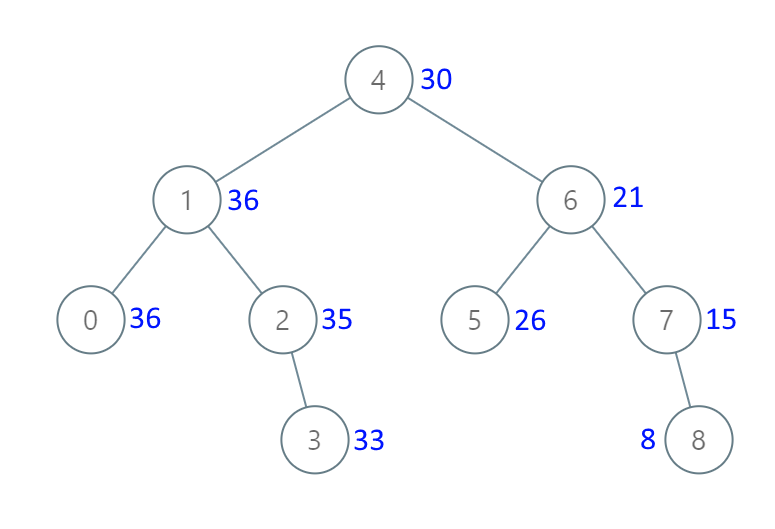
欧拉序-RMQ

欧拉序：其实就是dfs遍历的顺序（要记录出入）
设$E[i]$为欧拉序中第$i$个节点
$pos[i]$为节点$i$在欧拉序中第一次出现的索引

不妨假设$pos\left(u\right)<pos\left(v\right)$,则
p o s ( L C A ( u , v ) ) = min ⁡ { p o s ( k ) ∣ k ∈ E [ p o s ( u ) ⋯ p o s ( v ) ] } pos\left(LCA\left(u,v\right)\right) = \min\left\{pos\left(k\right)|k\in E\left[pos\left(u\right)\cdots pos\left(v\right)\right]\right\} pos(LCA(u,v))=min{pos(k)∣k∈E[pos(u)⋯pos(v)]}

举个例子

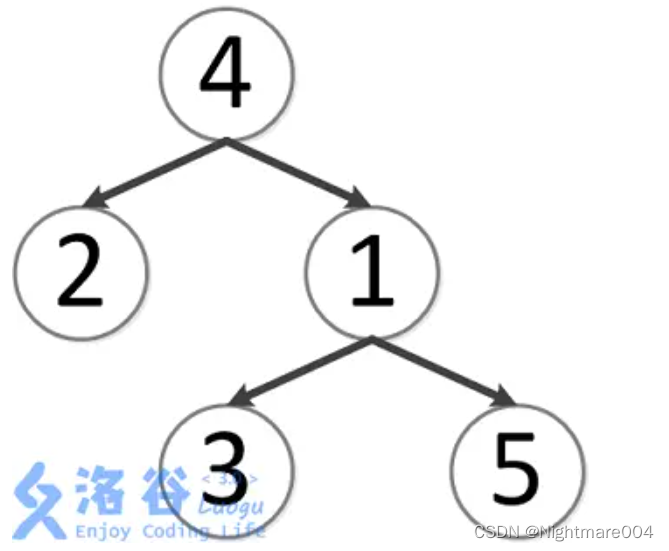
node	1	2	3	4	5
pos	4	2	5	1	7

idx	1	2	3	4	5	6	7	8	9
euler	4	2	4	1	3	1	5	1	4
pos	1	2	1	4	5	4	7	4	1

加粗表示第一次出现
比如$2,5$,欧拉序索引为$2,7$，欧拉序中$2,3,\cdots ,7$中$pos$最小的是4

所以现在问题就是区间最小值，可以用st表

#include<cstdio>
#include<vector>
#include<algorithm>

using namespace std;

const int N = 500005;
const int M = 21;

vector<int> edge[N];

int logn[N << 1] = { -1, 0 };
int dfsn[N << 1], tot;//欧拉序
int pos[N];//节点i在欧拉序中第一次出现的位置
int st[N << 1][M];

void dfs(int now) {
	dfsn[++tot] = now;
	pos[now] = tot;
	for (int i = 0; i < edge[now].size(); ++i) {
		if (!pos[edge[now][i]]) {
			dfs(edge[now][i]);
			dfsn[++tot] = now;
		}
	}
}

void init_st() {
	for (int i = 1; i <= tot; ++i) {
		st[i][0] = dfsn[i];
	}
	
	for (int j = 1; j <= logn[tot]; ++j) {
		for (int i = 1; i + (1 << j) - 1 <= tot; ++i) {
			if (pos[st[i][j - 1]] < pos[st[i + (1 << (j - 1))][j - 1]]) {
				st[i][j] = st[i][j - 1];
			}
			else {
				st[i][j] = st[i + (1 << (j - 1))][j - 1];
			}
		}
	}
}

int main() {
	int n, m, s, x, y;
	scanf("%d%d%d", &n, &m, &s);

	for (int i = 1; i < n; ++i) {
		scanf("%d%d", &x, &y);
		edge[x].push_back(y);
		edge[y].push_back(x);
	}

	dfs(s);
	for (int i = 2; i <= tot; ++i)logn[i] = logn[i >> 1] + 1;
	init_st();
	while (m--) {
		scanf("%d%d", &x, &y);
		x = pos[x];
		y = pos[y];
		if (x > y)swap(x, y);
		int s = logn[y - x + 1];
		if (pos[st[x][s]] < pos[st[y - (1 << s) + 1][s]]) {
			printf("%d\n", st[x][s]);
		}
		else {
			printf("%d\n", st[y - (1 << s) + 1][s]);
		}
	}
	return 0;
}

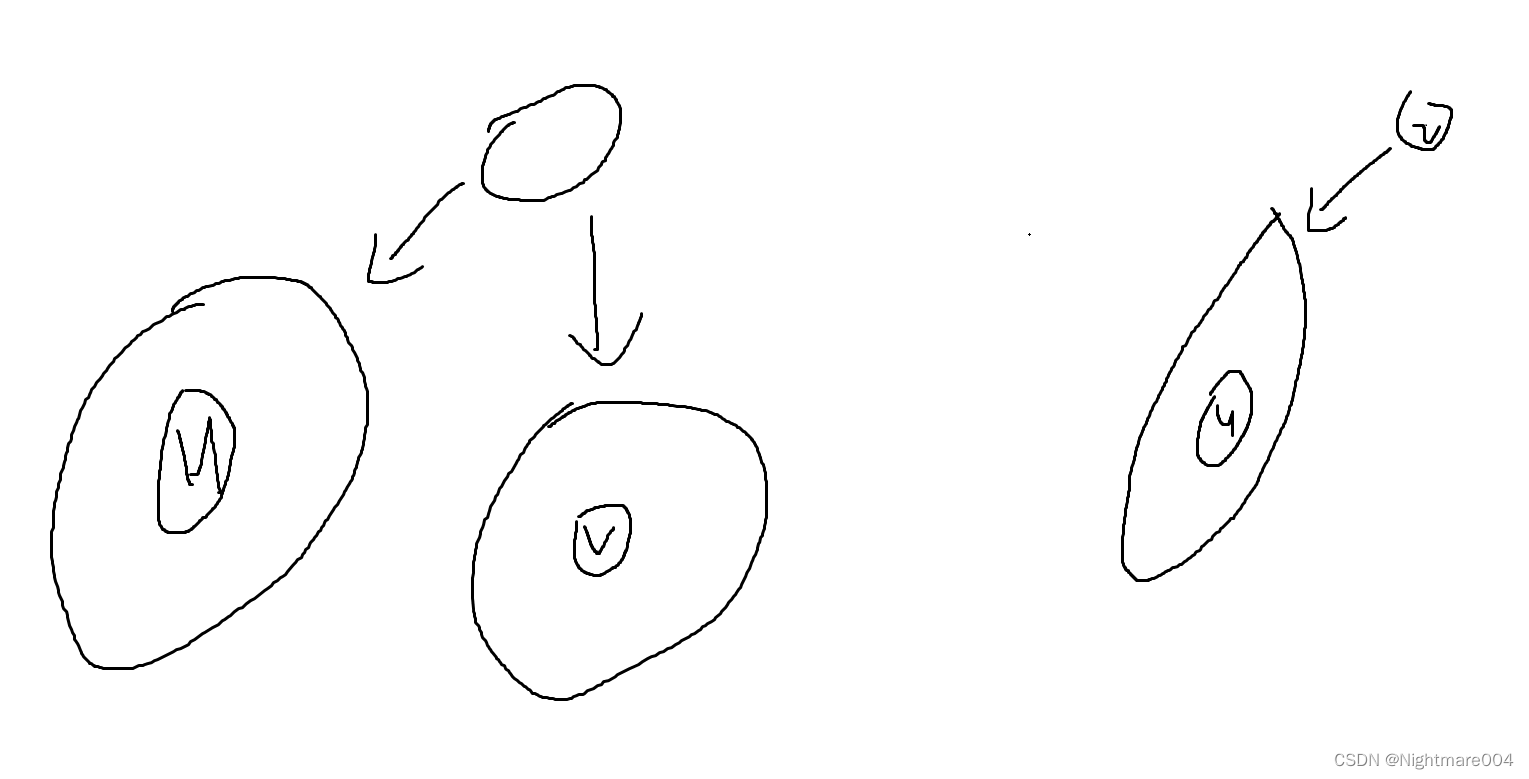
Tarjan

tarjan算法是一种离线的算法，使用并查集记录节点的祖先

dfs，当访问完v时，如果有查询是$(u,v)$,则他们的LCA为并查集中$u$的祖先
如下图

#include<cstdio>
#include<vector>
using namespace std;

const int N = 500005;
const int M = 500005;

vector<int> edge[N];
vector<pair<int, int> > query[M];//query[u] = (v,n) 表示第n个查询为(u,v)
int ans[M];//查询答案

bool visit[N];//访问
int parent[N];//并查集


int Find(int x) {
	int p = x;
	while (p != parent[p]) {
		p = parent[p];
	}

	while (x != p) {
		int y = parent[x];
		parent[x] = p;
		x = y;
	}
	return p;
}

void tarjan(int now) {
	parent[now] = now;
	visit[now] = true;
	for (int i = 0; i < edge[now].size(); ++i) {
		if (!visit[edge[now][i]]) {
			tarjan(edge[now][i]);
			
			parent[edge[now][i]] = now;
		}
	}

	for (int i = 0; i < query[now].size(); ++i) {
		int v = query[now][i].first;
		if (visit[v]) {
			ans[query[now][i].second >> 1] = Find(v);
		}
	}
}

int main() {
	int n, m, s, x, y;
	scanf("%d%d%d", &n, &m, &s);
	for (int i = 1; i < n; ++i) {
		scanf("%d%d", &x, &y);
		edge[x].push_back(y);
		edge[y].push_back(x);
	}

	for (int i = 0; i < m; ++i) {
		scanf("%d%d", &x, &y);
		query[x].push_back(make_pair(y, i << 1));
		query[y].push_back(make_pair(x, i << 1 | 1));
	}
	tarjan(s);
	for (int i = 0; i < m; ++i) {
		printf("%d\n", ans[i]);
	}
	return 0;
}

参考：
https://en.wikipedia.org/wiki/Lowest_common_ancestor