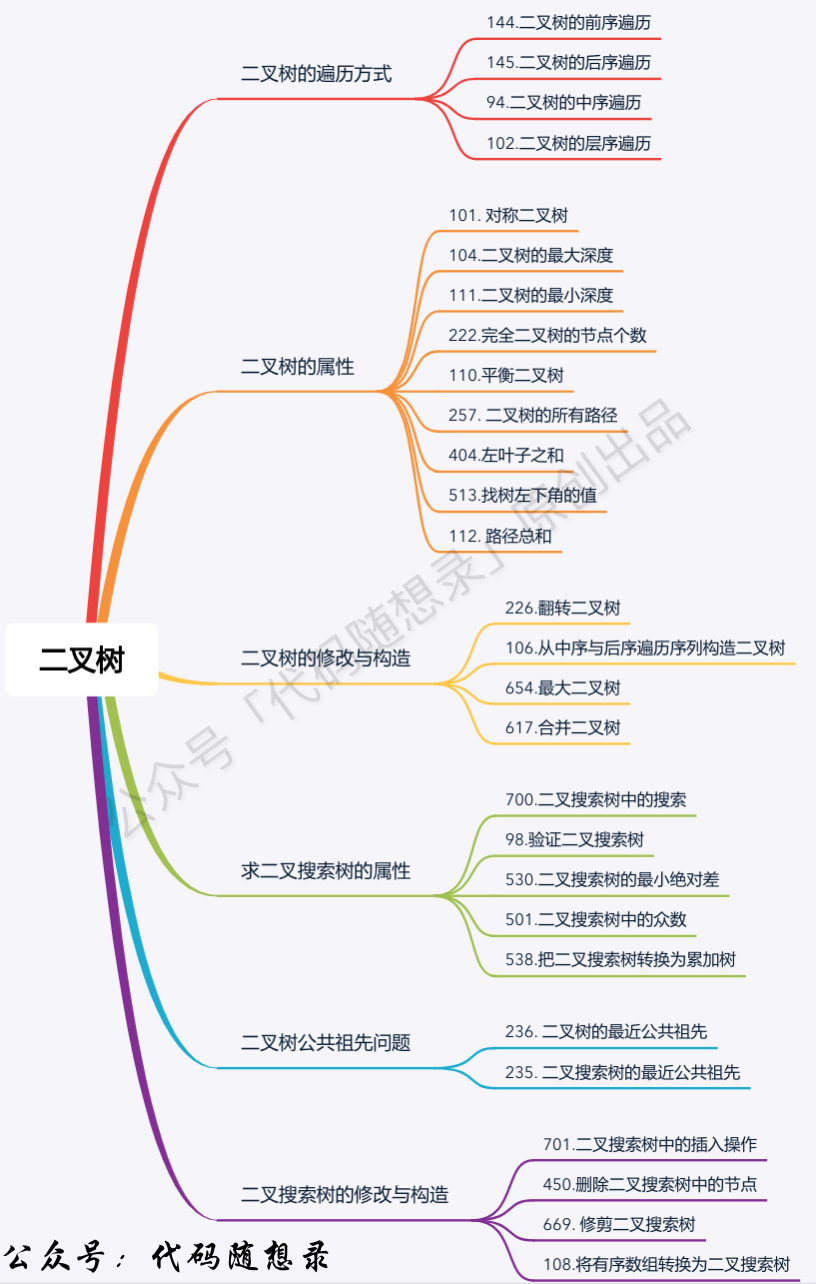
文章目录
- 零、二叉树理论
- 二叉树的种类
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 平衡二叉搜索树
- 二叉树的存储方式
- 二叉树的遍历方式
- 二叉树的定义
- 总结
- 一、二叉树的遍历
- [144. 二叉树的前序遍历 ](https://leetcode.cn/problems/binary-tree-preorder-traversal/)
- 题解
- 递归实现
- 迭代实现
- [94. 二叉树的中序遍历](https://leetcode.cn/problems/binary-tree-inorder-traversal/)
- 题解
- 递归解法
- 迭代解法
- [145. 二叉树的后序遍历](https://leetcode.cn/problems/binary-tree-postorder-traversal/description/)
- 题解
- 题解1:递归法
- 题解2:迭代法
- [102. 二叉树的层序遍历 ](https://leetcode.cn/problems/binary-tree-level-order-traversal/)
- 题解
- [429. N 叉树的层序遍历](https://leetcode.cn/problems/n-ary-tree-level-order-traversal/)
- 题解
- [589. N 叉树的前序遍历](https://leetcode.cn/problems/n-ary-tree-preorder-traversal/)
- 题解
- 递归法
- 迭代法
- [590. N 叉树的后序遍历 ](https://leetcode.cn/problems/n-ary-tree-postorder-traversal/)
- 题解
- 递归法
- 迭代法
- 二、二叉树的属性
- [101. 对称二叉树](https://leetcode.cn/problems/symmetric-tree/)
- 题解
- 递归法
- 迭代法-队列
- 迭代法-栈
- [100. 相同的树 ](https://leetcode.cn/problems/same-tree/description/)
- 题解
- [572. 另一棵树的子树 ](https://leetcode.cn/problems/subtree-of-another-tree/)
- 题解
- [104. 二叉树的最大深度 ](https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/)
- 题解
- 后序遍历递归
- 前序遍历递归
- 迭代法
- [559. N 叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/description/)
- 题解
- 递归法
- 迭代法
- [111. 二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/)
- 题解
- 递归法
- 迭代法
- [222. 完全二叉树的节点个数 ](https://leetcode.cn/problems/count-complete-tree-nodes/)
- 题解
- 1. 普通二叉树解法
- 递归法
- 迭代法
- 2. 完全二叉树解法
- [110. 平衡二叉树 ](https://leetcode.cn/problems/balanced-binary-tree/description/)
- 题解
- [257. 二叉树的所有路径 ](https://leetcode.cn/problems/binary-tree-paths/)
- 题解
- 递归法
- 迭代法
- [404. 左叶子之和 ](https://leetcode.cn/problems/sum-of-left-leaves/)
- 题解
- 递归法
- 迭代法
- [513. 找树左下角的值 ](https://leetcode.cn/problems/find-bottom-left-tree-value/)
- 题解
- 递归
- 迭代
- [112. 路径总和 ](https://leetcode.cn/problems/path-sum/description/)
- 题解
- 递归法
- 迭代法
- [113. 路径总和 II ](https://leetcode.cn/problems/path-sum-ii/)
- 题解
- 三、二叉树的修改与改造
- [226. 翻转二叉树 ](https://leetcode.cn/problems/invert-binary-tree/)
- 题解
- 1.深度优先遍历-递归
- 2.深度优先遍历-迭代
- 3.广度优先遍历
- [105. 从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
- 题解
- 优化前:每轮需要找根节点位置
- 优化后:哈希表记录根节点位置
- [106. 从中序与后序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/)
- 题解
- [654. 最大二叉树 ](https://leetcode.cn/problems/maximum-binary-tree/description/)
- 题解
- [617. 合并二叉树 ](https://leetcode.cn/problems/merge-two-binary-trees/)
- 题解
- 递归
- 迭代
- 四、二叉搜索树的属性
- [700. 二叉搜索树中的搜索 ](https://leetcode.cn/problems/search-in-a-binary-search-tree/)
- 题解
- [98. 验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree/)
- 题解1:中序遍历有序
- 题解2:递归-不适用额外数组,递归中进行判断
- [530. 二叉搜索树的最小绝对差](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/)
- 题解
- 解法1:先转为有序数组
- 解法2:直接在中序递归遍历中处理
- 解法3:迭代法
- [501. 二叉搜索树中的众数 ](https://leetcode.cn/problems/find-mode-in-binary-search-tree/)
- 题解
- 解法1:普通二叉树解法
- 解法2:中序遍历有序-处理有序数列
- 五、二叉树公共祖先问题
- [236. 二叉树的最近公共祖先 ](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
- 题解
- [235. 二叉搜索树的最近公共祖先 ](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/)
- 题解
- 六、二叉搜索树的修改与改造
- [701. 二叉搜索树中的插入操作](https://leetcode.cn/problems/insert-into-a-binary-search-tree/)
- 题解
- [450. 删除二叉搜索树中的节点 ](https://leetcode.cn/problems/delete-node-in-a-bst/)
- 题解
- [669. 修剪二叉搜索树](https://leetcode.cn/problems/trim-a-binary-search-tree/)
- 题解
- [108. 将有序数组转换为二叉搜索树 ](https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/)
- 题解
- [538. 把二叉搜索树转换为累加树 ](https://leetcode.cn/problems/convert-bst-to-greater-tree/)
- 题解
零、二叉树理论
二叉树的种类
在我们解题过程中二叉树有两种主要的形式:满二叉树和完全二叉树。
满二叉树
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
如图所示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QBInXkoR-1675071115879)(assets/20200806185805576.png)]
这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
完全二叉树
什么是完全二叉树?
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
我来举一个典型的例子如题:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JTo19T9J-1675071115880)(assets/20200920221638903.png)]
相信不少同学最后一个二叉树是不是完全二叉树都中招了。
之前我们刚刚讲过优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
下面这两棵树都是搜索树 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BVlGDIkA-1675071115881)(assets/20200806190304693.png)]
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DVHoD0bJ-1675071115881)(assets/20200806190511967.png)]
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。
所以大家使用自己熟悉的编程语言写算法,一定要知道常用的容器底层都是如何实现的,最基本的就是map、set等等,否则自己写的代码,自己对其性能分析都分析不清楚!
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在各个地址的节点串联一起。
链式存储如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uSFxTNaN-1675071115882)(assets/2020092019554618.png)]
链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JfZt0z37-1675071115883)(assets/20200920200429452.png)]
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
但是用链式表示的二叉树,更有利于我们理解,所以一般我们都是用链式存储二叉树。
所以大家要了解,用数组依然可以表示二叉树。
二叉树的遍历方式
关于二叉树的遍历方式,要知道二叉树遍历的基本方式都有哪些。
一些同学用做了很多二叉树的题目了,可能知道前中后序遍历,可能知道层序遍历,但是却没有框架。
我这里把二叉树的几种遍历方式列出来,大家就可以一一串起来了。
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式,后面在介绍图论的时候 还会介绍到。
那么从深度优先遍历和广度优先遍历进一步拓展,才有如下遍历方式:
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
在深度优先遍历中:有三个顺序,前中后序遍历, 有同学总分不清这三个顺序,经常搞混,我这里教大家一个技巧。
这里前中后,其实指的就是中间节点的遍历顺序,只要大家记住 前中后序指的就是中间节点的位置就可以了。
看如下中间节点的顺序,就可以发现,中间节点的顺序就是所谓的遍历方式
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
大家可以对着如下图,看看自己理解的前后中序有没有问题。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZTeQ51ki-1675071115883)(assets/20200806191109896.png)]
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
之前我们讲栈与队列的时候,就说过栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
这里其实我们又了解了栈与队列的一个应用场景了。
具体的实现我们后面都会讲的,这里大家先要清楚这些理论基础。
二叉树的定义
刚刚我们说过了二叉树有两种存储方式顺序存储,和链式存储,顺序存储就是用数组来存,这个定义没啥可说的,我们来看看链式存储的二叉树节点的定义方式。
C++代码如下:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
大家会发现二叉树的定义 和链表是差不多的,相对于链表 ,二叉树的节点里多了一个指针, 有两个指针,指向左右孩子。
这里要提醒大家要注意二叉树节点定义的书写方式。
在现场面试的时候 面试官可能要求手写代码,所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。
因为我们在刷leetcode的时候,节点的定义默认都定义好了,真到面试的时候,需要自己写节点定义的时候,有时候会一脸懵逼!
总结
二叉树是一种基础数据结构,在算法面试中都是常客,也是众多数据结构的基石。
本篇我们介绍了二叉树的种类、存储方式、遍历方式以及定义,比较全面的介绍了二叉树各个方面的重点,帮助大家扫一遍基础。
说到二叉树,就不得不说递归,很多同学对递归都是又熟悉又陌生,递归的代码一般很简短,但每次都是一看就会,一写就废。
一、二叉树的遍历
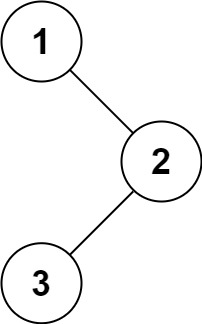
144. 二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
**进阶:**递归算法很简单,你可以通过迭代算法完成吗?
题解
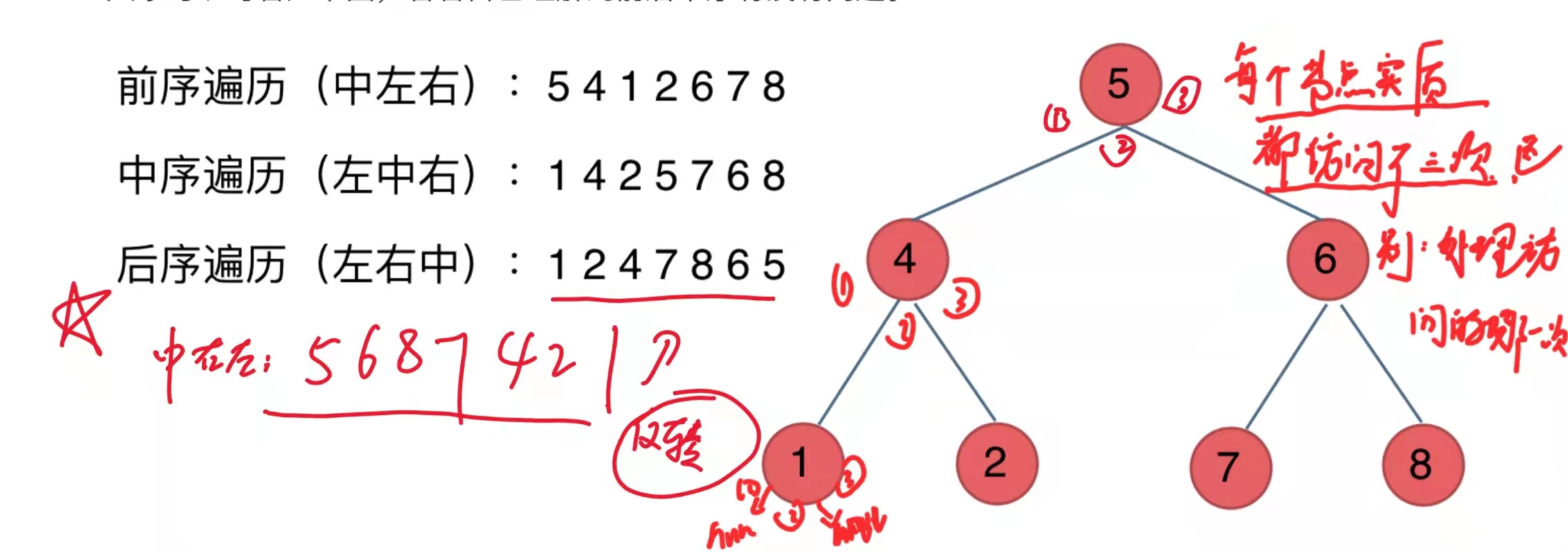
递归实现
-
处理子节点时,要循环遍历将每个子节点深度递归
-
其实,每个节点在递归调用时,都被访问了三次,三种遍历,区别只是再哪一次访问时进行处理
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if(root == nullptr) return ans;
dfs(root);
return ans;
}
private:
vector<int> ans;
void dfs(TreeNode* root) {
if(root == nullptr) return;
ans.push_back(root->val);
dfs(root->left); dfs(root->right);
}
};
迭代实现
- 使用栈,先序遍历,访问与处理同步
- 对子节点压入栈时,要注意顺序,后进先出,故,要从右往左压
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if(root == nullptr) return ans;
// 使用栈,压入节点,第一次访问节点时弹出栈处理
stack<TreeNode*> st;
// 1.先将根节点入栈
st.push(root);
while(!st.empty()) {
// 2.每次压入左右节点前,先弹出栈顶元素进行处理
TreeNode* cur = st.top(); st.pop(); ans.push_back(cur->val);
// 3.压入节点的子树,注意顺序颠倒,并注意边界,栈中元素不能为空
if(cur->right) st.push(cur->right);
if(cur->left) st.push(cur->left);
}
return ans;
}
private:
vector<int> ans;
};
94. 二叉树的中序遍历
- 给定一个二叉树的根节点
root,返回 它的 中序 遍历 。
题解
递归解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
if(root == nullptr) return ans;
dfs(root);
return ans;
}
private:
vector<int> ans;
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root -> left);
ans.push_back(root->val);
dfs(root->right);
}
};
迭代解法
-
用栈模拟递归深入遍历
-
1.由于访问的的顺序和处理的顺序不一致,需要使用指针指向要处理的节点
-
2.先访问:用指针,指向左分支中每个要访问的节点,先不处理,而是放入栈中,一直深到最左位置
- 初始stack为null,先不能加cur,与后面判断逻辑冲突
- 故要让循环能开始,需要再给定一个开始条件cur!=null;
-
3.再处理;指针指向要处理的节点,即栈顶元素
- 因为左边都访问完了,回到头节点的第二次访问时机进行处理
-
4.指针指向处理节点的右节点,以此节点为根节点,继续下一轮的访问处理,
-
维持左中右遍历顺序
/* ... / \ cur / \ null right / \ ... */
-
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
if(root == nullptr) return ans;
// 1.使用栈模拟压入节点,处理节点,指针指向访问的节点
stack<TreeNode*> st;
TreeNode* curPt = root;
// 2.先压栈访问到最深处,为保持代码一致,根节点在循环内入栈
while(curPt != nullptr || !st.empty()) {
// 2.1 先入栈,更新访问指针
while(curPt != nullptr) {
st.push(curPt);
curPt = curPt->left; // 一直找左边最深处
}
// 2.2 处理找到的最左节点
curPt = st.top(); st.pop();ans.push_back(curPt->val);
// 2.3 处理完后,寻找右节点,维持左中右顺序
curPt = curPt->right;
}
return ans;
}
private:
vector<int> ans;
};
145. 二叉树的后序遍历
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
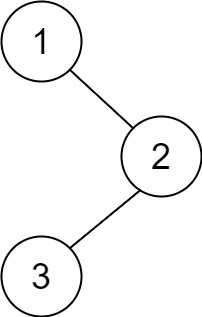
输入:root = [1,null,2,3]
输出:[3,2,1]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
- 树中节点的数目在范围
[0, 100]内 -100 <= Node.val <= 100
**进阶:**递归算法很简单,你可以通过迭代算法完成吗?
题解
题解1:递归法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
if(root == nullptr) return ans;
dfs(root);
return ans;
}
private:
vector<int> ans;
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root->left); dfs(root->right);ans.push_back(root->val);
}
};
题解2:迭代法
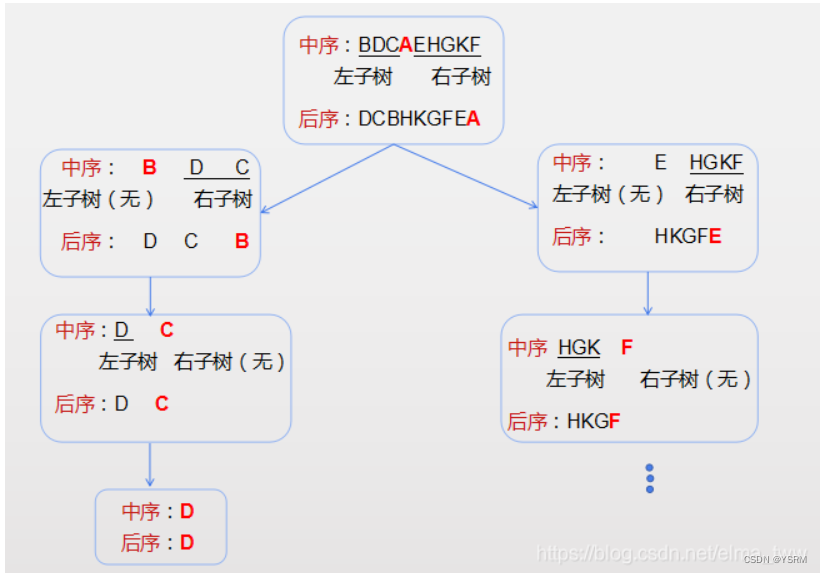
- 先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了,如下图:

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
if(root == nullptr) return ans;
stack<TreeNode*> st;
st.push(root);
while(!st.empty()) {
TreeNode* cur = st.top(); st.pop(); ans.push_back(cur->val);
// 注意顺序,先改成头右左,再反转就是左右头,后续遍历
if(cur->left) st.push(cur->left);
if(cur->right) st.push(cur->right);
}
reverse(ans.begin(), ans.end());
return ans;
}
private:
vector<int> ans;
};
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
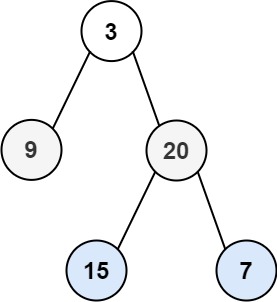
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
题解
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
if(root == NULL) return ans;
// 1.使用队列,先将根节点入队
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
// 2.入左右子树前,先将队列中的一层元素取出
int size = que.size();
vector<int> arr;
while(size-- > 0) {
TreeNode* cur = que.front(); que.pop();
arr.push_back(cur->val);
// 3.弹出后,将头节点的子节点压入队列
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
ans.push_back(arr);
}
return ans;
}
};
429. N 叉树的层序遍历
-
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
-
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:

题解
- 对于层序遍历,可以使用FIFO的队列来处理
- 因为每一层一共处理,因此,队列中储存的元素,要多维护一个变量,即层数,因此储存二元组
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
queue<Node*> que;
vector<vector<int>> ans;
if(root == NULL) return ans;
que.push(root);
while(!que.empty()) {
int size = que.size();
vector<int> arr;
while(size-- > 0) {
Node* cur = que.front(); que.pop();
arr.push_back(cur->val);
for(Node* child : cur->children) {
que.push(child);
}
}
ans.push_back(arr);
}
return ans;
}
};
589. N 叉树的前序遍历
给定一个 n 叉树的根节点 root ,返回 其节点值的 前序遍历 。
n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
示例 1:
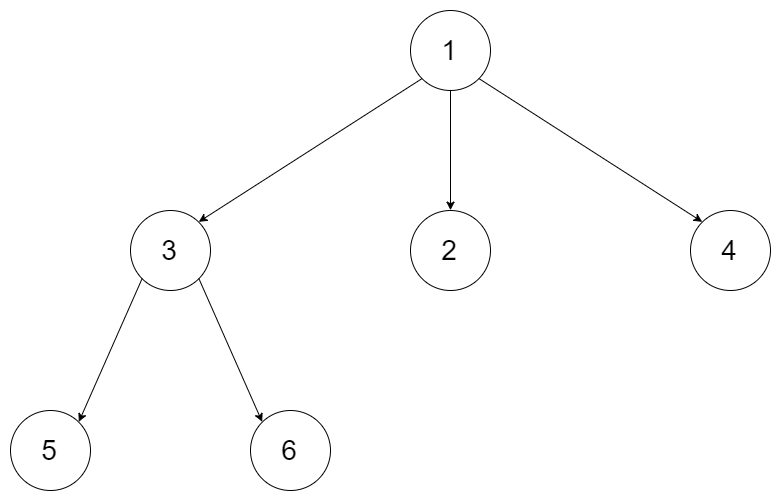
输入:root = [1,null,3,2,4,null,5,6]
输出:[1,3,5,6,2,4]
示例 2:
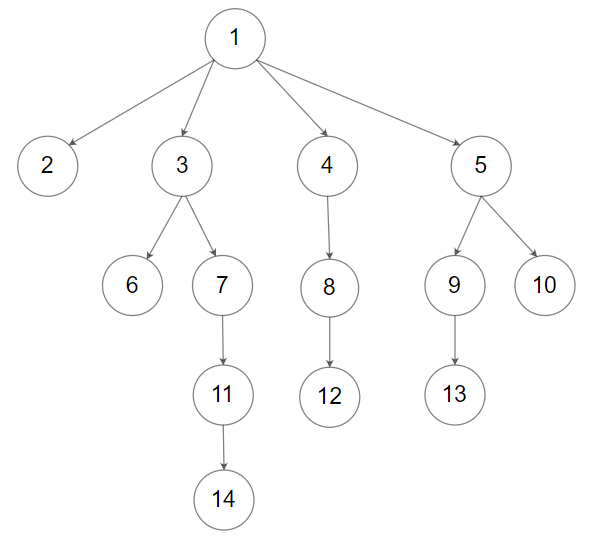
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出:[1,2,3,6,7,11,14,4,8,12,5,9,13,10]
提示:
- 节点总数在范围
[0, 104]内 0 <= Node.val <= 104- n 叉树的高度小于或等于
1000
**进阶:**递归法很简单,你可以使用迭代法完成此题吗?
题解
递归法
class Solution {
public:
vector<int> ans;
vector<int> preorder(Node* root) {
if(root == NULL) return ans;
dfs(root);
return ans;
}
void dfs(Node* root) {
if(root == NULL) return;
ans.push_back(root->val);
for(Node* child : root->children) {
dfs(child);
}
}
};
迭代法
class Solution {
public:
vector<int> ans;
vector<int> preorder(Node* root) {
if(root == NULL) return ans;
stack<Node*> st;
st.push(root);
while(!st.empty()) {
Node* cur = st.top(); st.pop(); ans.push_back(cur->val);
for(int i = cur->children.size() - 1; i >= 0; i--) {
if(cur->children[i] != NULL) st.push(cur->children[i]);
}
}
return ans;
}
};
590. N 叉树的后序遍历
给定一个 n 叉树的根节点 root ,返回 其节点值的 后序遍历 。
n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
示例 1:
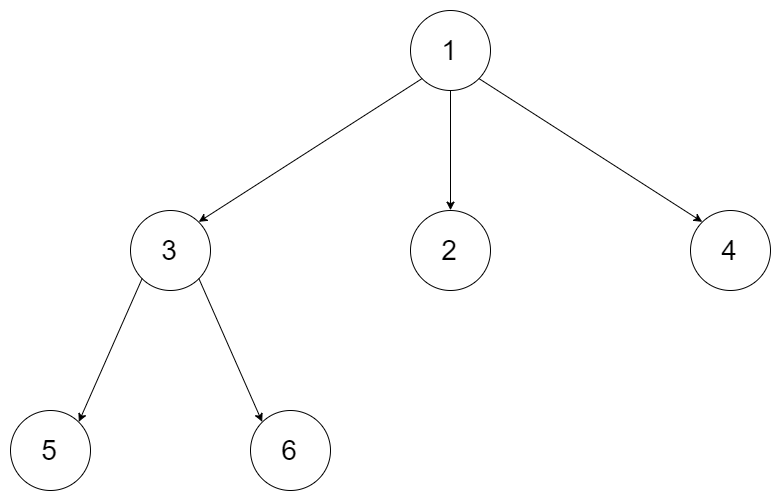
输入:root = [1,null,3,2,4,null,5,6]
输出:[5,6,3,2,4,1]
示例 2:
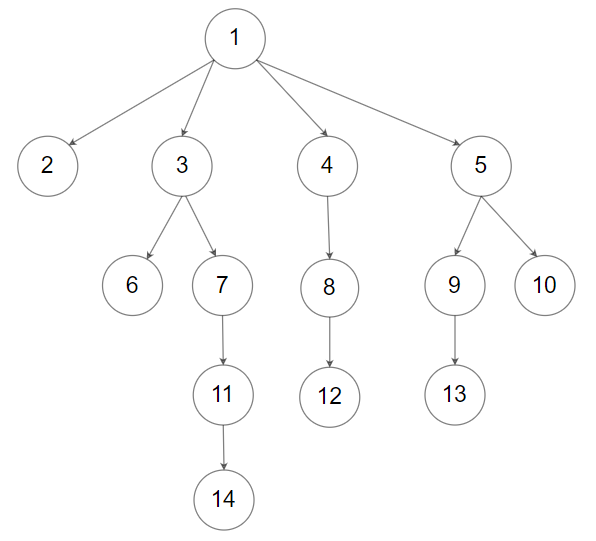
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出:[2,6,14,11,7,3,12,8,4,13,9,10,5,1]
提示:
- 节点总数在范围
[0, 104]内 0 <= Node.val <= 104- n 叉树的高度小于或等于
1000
**进阶:**递归法很简单,你可以使用迭代法完成此题吗?
题解
递归法
class Solution {
public:
vector<int> ans;
vector<int> postorder(Node* root) {
if(root == NULL) return ans;
dfs(root);
return ans;
}
void dfs(Node* root) {
if(root == NULL) return;
for(Node* child : root->children) dfs(child);
ans.push_back(root->val);
}
};
迭代法
class Solution {
public:
vector<int> ans;
vector<int> postorder(Node* root) {
if(root == NULL) return ans;
stack<Node*> st;
st.push(root);
while(!st.empty()) {
Node* cur = st.top(); st.pop(); ans.push_back(cur->val);
for(auto child : cur->children) {
if(child) st.push(child);
}
}
reverse(ans.begin(), ans.end());
return ans;
}
};
二、二叉树的属性
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
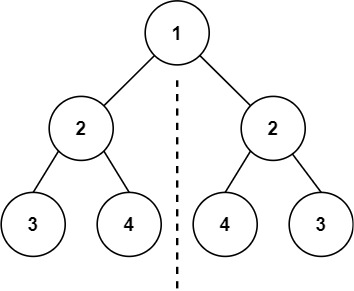
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
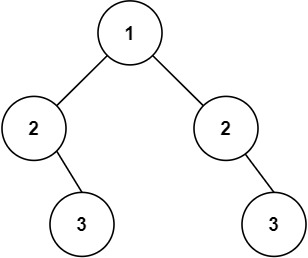
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
**进阶:**你可以运用递归和迭代两种方法解决这个问题吗?
题解
正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。
递归法
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == NULL) return true;
return compare(root->left, root->right);
}
bool compare(TreeNode* left, TreeNode* right) {
if(left != NULL && right == NULL) return false;
else if(left == NULL && right != NULL) return false;
else if(left == NULL && right == NULL) return true;
else if(left->val != right->val) return false;
else return compare(left->left, right->right)
&& compare(left->right, right->left);
}
};
- 简易代码
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == NULL) return true;
return compare(root->left, root->right);
}
bool compare(TreeNode* left, TreeNode* right) {
if(!left && !right) return true; // 都为NULL,cpp的false即为null,true极为!=NULL
else if(!left || !right || left->val != right->val) return false;
else return compare(left->left, right->right)
&& compare(left->right, right->left);
}
};
迭代法-队列
实质是两两比较,用队列或栈都可以,关键是入队的顺序的设定
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == NULL) return true;
queue<TreeNode*> que; // 或者用stack也一样
// 主要判断左右子树,需要将左右子树放入队列中
que.push(root->left); que.push(root->right);
while(!que.empty()) {
TreeNode* left = que.front(); que.pop();
TreeNode* right = que.front(); que.pop();
if(!left && !right) continue; // 不要返回,要继续判断
if(!left || !right || left->val != right->val) return false;
que.push(left->left); que.push(right->right);
que.push(left->right); que.push(right->left);
}
return true;
}
};
迭代法-栈
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
stack<TreeNode*> st; // 这里改成了栈
st.push(root->left);
st.push(root->right);
while (!st.empty()) {
TreeNode* leftNode = st.top(); st.pop();//其实为右,但都可以,只要左右就行
TreeNode* rightNode = st.top(); st.pop();
if (!leftNode && !rightNode) {
continue;
}
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
st.push(leftNode->left);
st.push(rightNode->right);
st.push(leftNode->right);
st.push(rightNode->left);
}
return true;
}
};
100. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
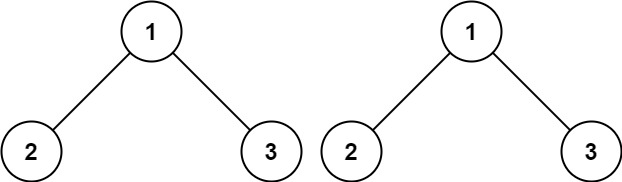
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
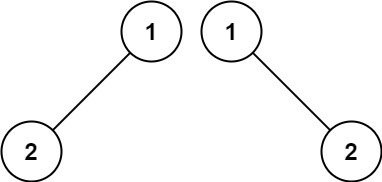
输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
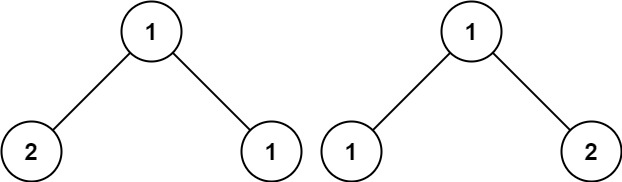
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
- 两棵树上的节点数目都在范围
[0, 100]内 -104 <= Node.val <= 104
题解
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(!p && !q) return true;
else if(!p || !q || p->val != q->val) return false;
else return isSameTree(p->left, q->left) &&
isSameTree(p->right, q->right);
}
};
572. 另一棵树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
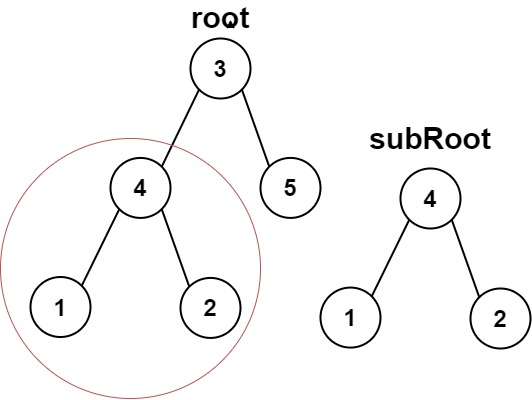
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
示例 2:
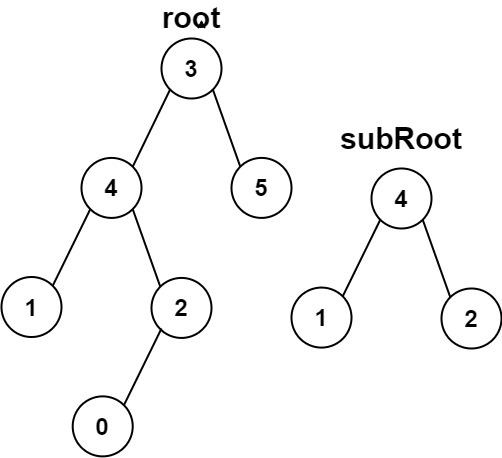
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出:false
提示:
root树上的节点数量范围是[1, 2000]subRoot树上的节点数量范围是[1, 1000]-104 <= root.val <= 104-104 <= subRoot.val <= 104
题解
本题需要两个递归:
-
1.递归判断两个树是否相等:
- 如果
root所在树和subRoot所在树完全相同,则直接返回true。
- 如果
-
2.递归截取root的子树:
- 否则,就分别判断
root的左子树和右子树是否和subRoot所在树完全相同。
- 否则,就分别判断
class Solution {
public:
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
// 1.递归1:截取root的子树-先检查根,再递归左右子树进行截取
if(!root) return false; // root树先遍历完,一定没有匹配上
// 2.递归2:递归判断root截取的子树是否与subRoot相同-一直要递归到最深处才能判断
return check(root, subRoot)
|| isSubtree(root->left, subRoot)
|| isSubtree(root->right, subRoot); // 只要找到一个子树即可
}
bool check(TreeNode* left, TreeNode* right) {
// 1.递归终止条件处理
if(!left && !right) return true;
// 2.当前逻辑处理
else if(!left || !right || left->val != right->val) return false;
// 3.下轮递归参数设置
else return check(left->left, right->left)
&& check(left->right, right->right);
}
};
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
题解
后序遍历递归
本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,使用后序求的是高度。
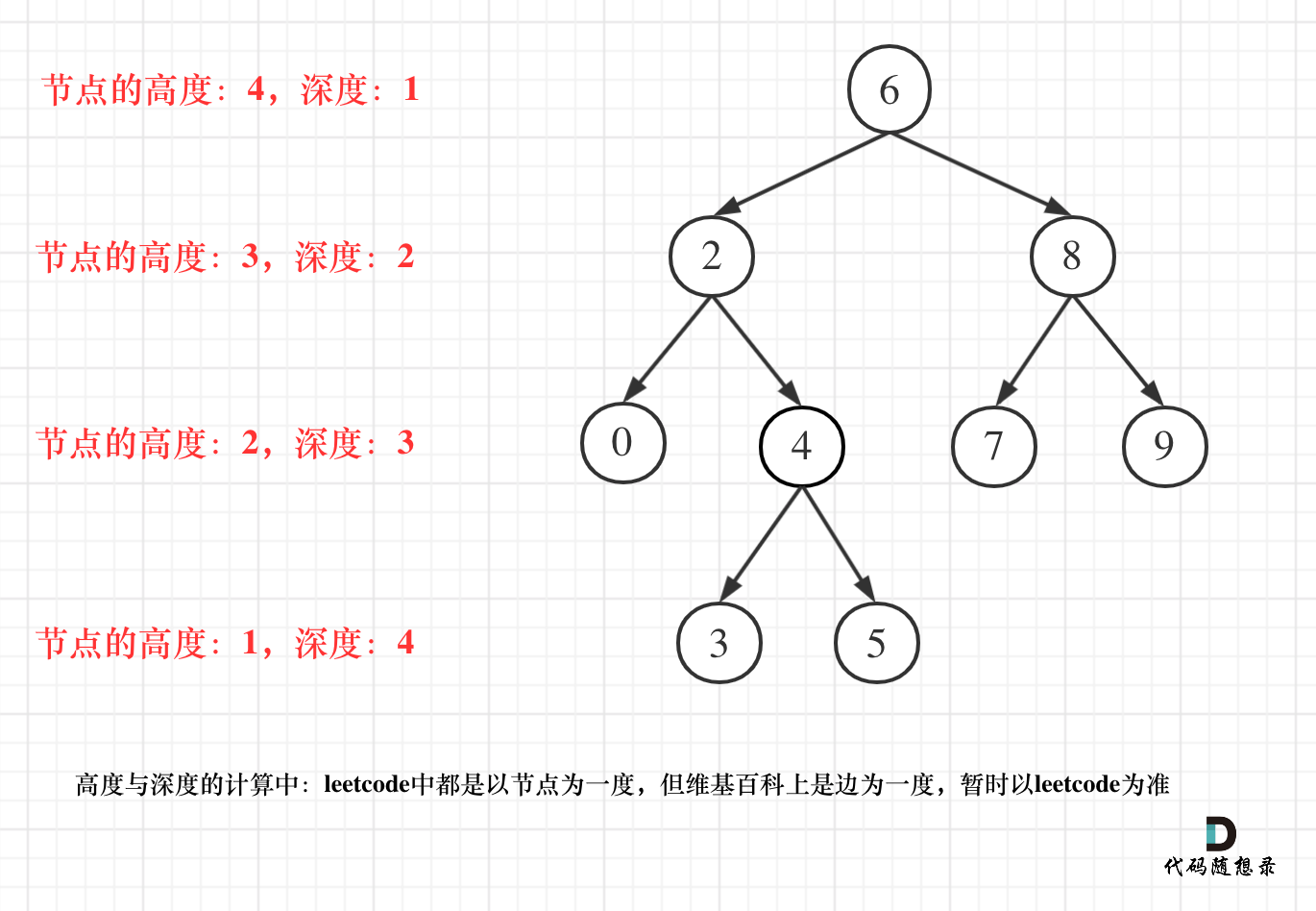
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)
而根节点的高度就是二叉树的最大深度,所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
1.确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
代码如下:
int getdepth(treenode* node)
**2.确定终止条件:**如果为空节点的话,就返回0,表示高度为0。
代码如下:
if (node == NULL) return 0;
**3.确定单层递归的逻辑:**先求它的左子树的深度,再求右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
代码如下:
int leftdepth = getdepth(node->left); // 左
int rightdepth = getdepth(node->right); // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;
整体代码如下:
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == NULL) return 0;
return getDepth(root);
}
// 1.确定递归函数的参数和返回值:根节点,返回根节点下的深度
int getDepth(TreeNode* root) {
// 2. 处理边界条件
if(root == NULL) return 0;
// 3.处理单层递归的逻辑
return 1 + max(getDepth(root->left), getDepth(root->right));
}
};
前序遍历递归
充分表现出求深度回溯的过程
class solution {
public:
int result;
void getdepth(treenode* node, int depth) {
result = depth > result ? depth : result; // 中
if (node->left == NULL && node->right == NULL) return ;
if (node->left) { // 左
depth++; // 深度+1
getdepth(node->left, depth);
depth--; // 回溯,深度-1
}
if (node->right) { // 右
depth++; // 深度+1
getdepth(node->right, depth);
depth--; // 回溯,深度-1
}
return ;
}
int maxdepth(treenode* root) {
result = 0;
if (root == NULL) return result;
getdepth(root, 1);
return result;
}
};
- 简化版:path设定为局部变量,按值传递,递归返回后,自动删除,无需手动删除回溯
class Solution {
public:
int result;
void getDepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // 中
if (node->left == NULL && node->right == NULL) return ;
if (node->left) { // 左
getDepth(node->left, depth + 1); // 参数depth没有变化,只是传入值改变
}
if (node->right) { // 右
getDepth(node->right, depth + 1);
}
return ;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == 0) return result;
getDepth(root, 1);
return result;
}
};
迭代法
使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
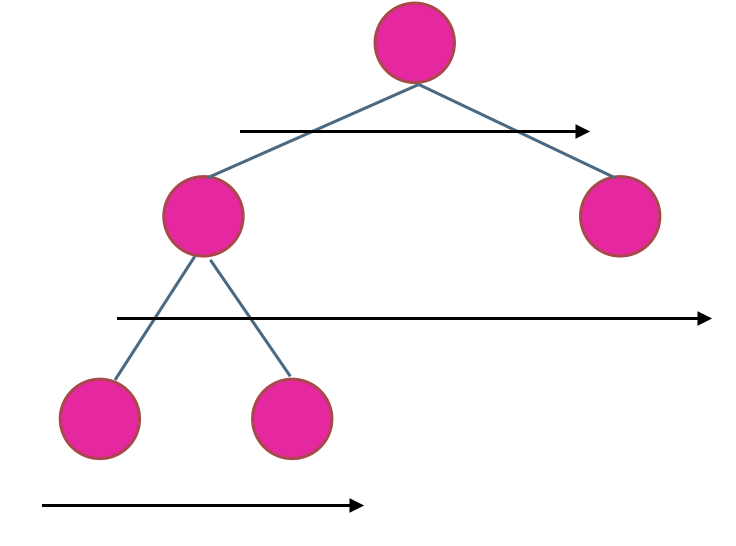
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == NULL) return 0;
// 1.用一个状态遍历维护深度
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
depth++; // 每遍历一层,记录层数-就是深度值
while(size-- > 0) {
TreeNode* cur = que.front(); que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return depth;
}
};
559. N 叉树的最大深度
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
示例 1:
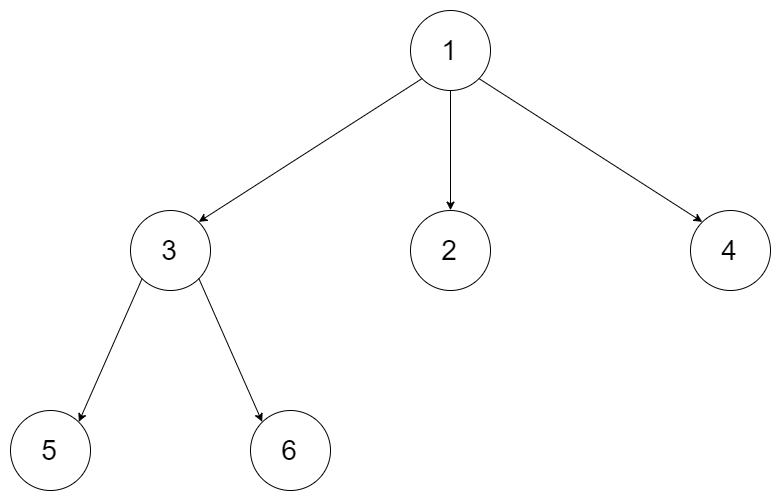
输入:root = [1,null,3,2,4,null,5,6]
输出:3
示例 2:
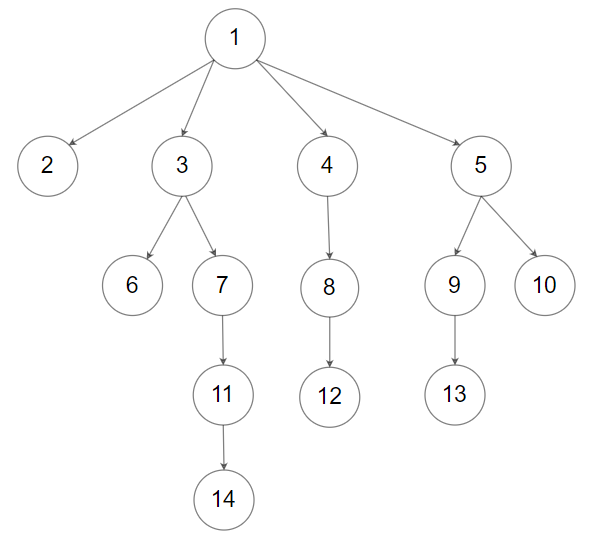
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出:5
提示:
- 树的深度不会超过
1000。 - 树的节点数目位于
[0, 104]之间。
题解
递归法
class Solution {
public:
int maxDepth(Node* root) {
if(root == NULL) return 0;
return getDepth(root);
}
int getDepth(Node* root) {
if(root == NULL) return 0;
int maxdp = 0;
for(Node* child : root->children)
maxdp = max(maxdp, getDepth(child));
return maxdp + 1;
}
};
迭代法
class Solution {
public:
int maxDepth(Node* root) {
if(root == NULL) return 0;
int depth = 0;
queue<Node*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
depth++;
while(size-- > 0) {
Node* cur = que.front(); que.pop();
for(Node* child : cur->children) {
if(child) que.push(child);
}
}
}
return depth;
}
};
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
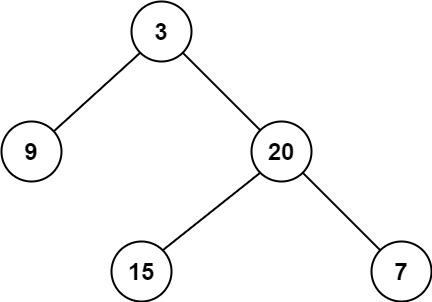
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
题解
注意:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。
递归法
class Solution {
public:
int minDepth(TreeNode* root) {
return getDepth(root);
}
int getDepth(TreeNode* root) {
if(root == NULL) return 0;
// 到叶子节点的最短路径,要找到叶子节点
if(root->left == NULL && root->right != NULL) {
return 1 + getDepth(root->right);
}
if(root->right == NULL && root->left != NULL) {
return 1 + getDepth(root->left);
}
return 1 + min(getDepth(root->left), getDepth(root->right));
}
};
迭代法
需要注意的是,只有当左右孩子都为空的时候,才说明遍历到最低点了。如果其中一个孩子不为空则不是最低点
class Solution {
public:
int minDepth(TreeNode* root) {
if(root == NULL) return 0;
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
depth++;
while(size-- > 0) {
TreeNode* node = que.front(); que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
// 当左右孩子都为空的时候,说明是最低点的一层了,返回结果
if(!node->left && !node->right) return depth;
}
}
return depth;
}
};
222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
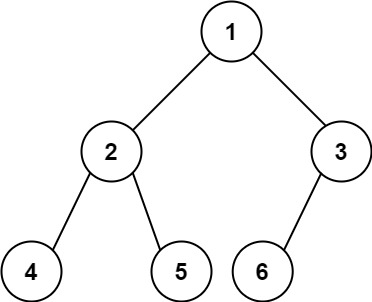
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
- 树中节点的数目范围是
[0, 5 * 104] 0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
**进阶:**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
题解
1. 普通二叉树解法
首先按照普通二叉树的逻辑来求。
这道题目的递归法和求二叉树的深度写法类似, 而迭代法,二叉树:层序遍历登场! (opens new window)遍历模板稍稍修改一下,记录遍历的节点数量就可以了。
递归遍历的顺序依然是后序(左右中)。
递归法
class Solution {
public:
int countNodes(TreeNode* root) {
return getNodes(root);
}
int getNodes(TreeNode* root) {
if(root == NULL) return 0;
return getNodes(root->left) + getNodes(root->right) + 1;
}
};
迭代法
class Solution {
public:
int countNodes(TreeNode* root) {
if(root == NULL) return 0;
queue<TreeNode*> que;
que.push(root);
int count = 0;
while(!que.empty()) {
int size = que.size();
count += size; // 统计每层的节点数量,也可以在后面找到每个节点后加
while(size-- > 0) {
TreeNode* node = que.front(); que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return count;
}
};
2. 完全二叉树解法
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
判断其子树是不是满二叉树,如果是则利用公式计算这个子树(满二叉树)的节点数量,如果不是则继续递归
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 1, rightDepth = 1; //深度初始为根节点1
while (left) { // 求左子树深度
left = left->left;
leftDepth++;
}
while (right) { // 求右子树深度
right = right->right;
rightDepth++;
}
// 1.如果左右子树深度一样,就是满二叉树,节点为2^depth-1
if (leftDepth == rightDepth) {
return (2 << (leftDepth-1) - 1; // 注意(2<<1) 相当于2^2,所应要少移动一位
}
// 2.如果深度不一样,说明不满,分别找左右子树的满二叉树的值
return countNodes(root->left)) + countNodes(root->right) + 1;
}
};
- 时间复杂度:O(log n × log n)
- 空间复杂度:O(log n)
110. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
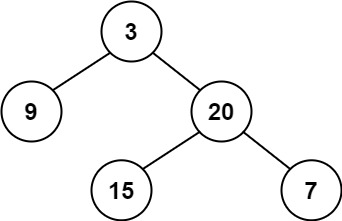
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
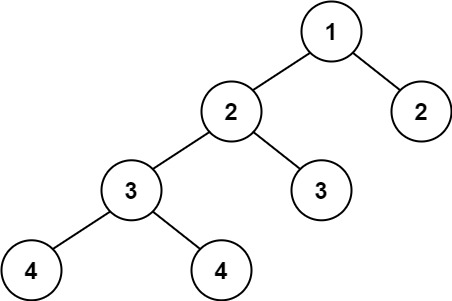
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
题解
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图:
-
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
-
既然要求比较高度,必然是要后序遍历
class Solution {
public:
bool isBalanced(TreeNode* root) {
if(root == NULL) return true;
return getHeight(root) == -1 ? false : true;
}
// 1.递归参数,返回值:返回平衡二叉树根节点的高度,并以-1标志已经不是平衡
int getHeight(TreeNode* root) {
// 2.终止条件:为null时,遍历到了最深处,返回0
if(root == NULL) return 0;
// 3. 本层逻辑,统计左右子树高度,判断并更新根节点高度
int lH = getHeight(root->left), rH = getHeight(root->right);
if(lH == -1) return -1;
if(rH == -1) return -1;
return abs(lH - rH) > 1 ? -1 : 1 + max(lH, rH);
}
};
257. 二叉树的所有路径
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
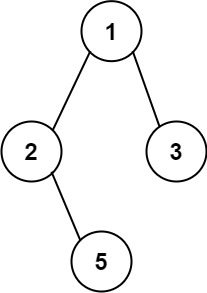
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]
提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
题解
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
递归法
class Solution {
public:
vector<string> ans;
vector<int> path;
vector<string> binaryTreePaths(TreeNode* root) {
if(root == NULL) return ans;
getPath(root);
return ans;
}
// 1. 递归参数:节点和结果容器
void getPath(TreeNode* root) {
// 2.递归终止:找到叶子节点,因此,要先将叶子节点加入path中
path.push_back(root->val);
if(!root->left && !root->right) { // 到叶子节点,找到一条路径
string str;
for(int i = 0; i < path.size() - 1; i++) {
str += to_string(path[i]); str += "->";
}
str += to_string(path[path.size() - 1]);
ans.push_back(str);
return; // 递归终止,切记不要忘,否则递归无法结束
}
// 3.本层逻辑,排除空节点,分别找左右分支-记得递归与回溯是一对
if(root->left) {
getPath(root->left);
path.pop_back();
}
if(root->right) {
getPath(root->right);
path.pop_back();
}
}
};
迭代法
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
stack<TreeNode*> treeSt;// 保存树的遍历节点
stack<string> pathSt; // 保存遍历路径的节点
vector<string> result; // 保存最终路径集合
if (root == NULL) return result;
treeSt.push(root);
pathSt.push(to_string(root->val));
while (!treeSt.empty()) {
TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
string path = pathSt.top();pathSt.pop(); // 取出该节点对应的路径
if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
result.push_back(path);
}
if (node->right) { // 右
treeSt.push(node->right);
pathSt.push(path + "->" + to_string(node->right->val));
}
if (node->left) { // 左
treeSt.push(node->left);
pathSt.push(path + "->" + to_string(node->left->val));
}
}
return result;
}
};
404. 左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
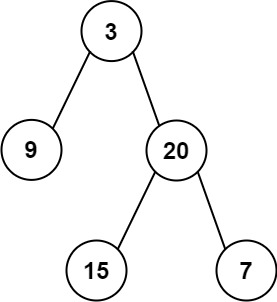
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0
提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
题解
解题思路是:先判断是否为左叶子节点,再进行累加
判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子
递归法
递归的遍历顺序为后序遍历(左右中),是因为要通过递归函数的返回值来累加求取左叶子数值之和
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if(root == NULL) return 0;
return dfs(root);
}
// 1.确定递归函数参数和返回值
int dfs(TreeNode* root) {
// 2.递归终止条件,节点为null,一条路走完了,且一定没有左叶子
if(root == NULL) return 0;
// 3.本层逻辑,寻找左右节点的左叶子节点数量
// 先找左叶子节点,处理完左边的左叶子节点后,再处理右边,找右边的左叶子节点
int leftSum = dfs(root->left);
// 本层逻辑还要找到左叶子节点,如果找到左叶子,返回左叶子节点值
if(root->left && !root->left->left && !root->left->right)
leftSum = root->left->val;
int rightSum = dfs(root->right);
return leftSum + rightSum;
}
};
迭代法
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return 0;
st.push(root);
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
if (node->left && !node->left->left && !node->left->right) {
result += node->left->val;
}
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
}
return result;
}
};
513. 找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
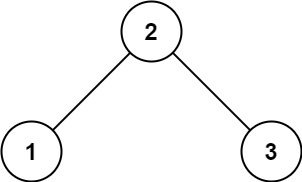
输入: root = [2,1,3]
输出: 1
示例 2:
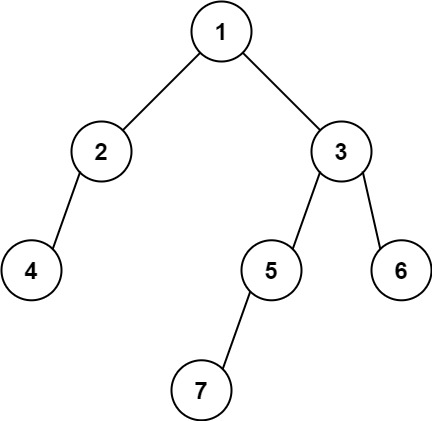
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
提示:
- 二叉树的节点个数的范围是
[1,104] -231 <= Node.val <= 231 - 1
题解
递归
如果使用递归法,如何判断是最后一行呢,其实就是深度最大的叶子节点一定是最后一行
如何找最左边的呢?可以使用前序遍历(当然中序,后序都可以,因为本题没有 中间节点的处理逻辑,只要左优先就行),保证优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
class Solution {
public:
int ans, maxDepth = INT_MIN;
int findBottomLeftValue(TreeNode* root) {
dfs(root, 1);
return ans;
}
// 1.参数与返回值:根节点与深度,只需遍历找到最深,更新答案
void dfs(TreeNode* root, int depth) {
// 2.递归终止
if(root == NULL) return;
// 3.本层逻辑-先判断更新答案,再深度递归左右子树
if(depth > maxDepth) { // 深度相同也不更新,保证每次找每层的最左边
maxDepth = depth;
ans = root->val;
}
dfs(root->left, depth + 1);
dfs(root->right, depth + 1);
}
};
- 事实上,只有遇到叶子节点时,深度才可能最大,因此,只需在叶子节点时更新即可
class Solution {
public:
int ans, maxDepth = INT_MIN;
int findBottomLeftValue(TreeNode* root) {
dfs(root, 1);
return ans;
}
// 1.参数与返回值:根节点与深度,只需遍历找到最深,更新答案
void dfs(TreeNode* root, int depth) {
// 2.递归终止
if(root == NULL) return;
// 3.本层逻辑-先判断更新答案,再深度递归左右子树
if(!root->left && !root->right) {
if(depth > maxDepth) {
maxDepth = depth;
ans = root->val;
}
}
dfs(root->left, depth + 1);
dfs(root->right, depth + 1);
}
};
迭代
本题使用层序遍历再合适不过了,比递归要好理解得多!
只需要记录最后一行第一个节点的数值就可以了。
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
int ans;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
for(int i = 0; i < size; i++) {
TreeNode* cur = que.front(); que.pop();
// 不太方便判断当前层为最后一层,每层都更新答案
if(i == 0) ans = cur->val;
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return ans;
}
};
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
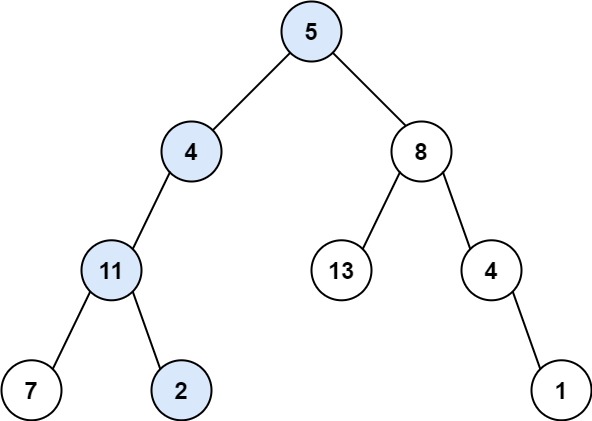
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kcNxhv0i-1675071115895)(https://assets.leetcode.com/uploads/2021/01/18/pathsum2.jpg)]
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
题解
递归法
- 因为要找一条路径,一旦找到了就返回,故递归函数需要有返回值
- 子树的结果要回溯到父节点,只要有一个分支是true,就向父节点返回true
- 需要找到叶子节点即可判断,因此,空节点不遍历处理,直接返回false
- 相对于累加,相减更便捷
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == NULL) return false;
return check(root, targetSum - root->val); // 相对于累加,相减更便捷
}
// 1.递归参数:根节点与count计数,返回bool
bool check(TreeNode* root, int count) {
// 2.递归终止:找到叶子节点,而不是空节点,少一层递归
if(!root->left && !root->right && count == 0) return true;
if(!root->left && !root->right) return false;
// 3.本层逻辑:先递归找左右子树,回溯结果
if(root->left) {
// 一旦找到,就返回
if(check(root->left, count - root->left->val)) return true;
}
if(root->right) {
if(check(root->right, count - root->right->val)) return true;
}
// 左右子树都不返回true,就向父节点返回false
return false;
}
};
迭代法
class solution {
public:
bool haspathsum(TreeNode* root, int sum) {
if (root == null) return false;
// 此时栈里要放的是pair<节点指针,路径数值>
stack<pair<TreeNode*, int>> st;
st.push(pair<TreeNode*, int>(root, root->val));
while (!st.empty()) {
pair<TreeNode*, int> node = st.top();
st.pop();
// 如果该节点是叶子节点了,同时该节点的路径数值等于sum,那么就返回true
if (!node.first->left && !node.first->right && sum == node.second)
return true;
// 右节点,压进去一个节点的时候,将该节点的路径数值也记录下来
if (node.first->right) {
st.push(pair<TreeNode*, int>
(node.first->right, node.second + node.first->right->val));
}
// 左节点,压进去一个节点的时候,将该节点的路径数值也记录下来
if (node.first->left) {
st.push(pair<TreeNode*, int>
(node.first->left, node.second + node.first->left->val));
}
}
return false;
}
};
113. 路径总和 II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
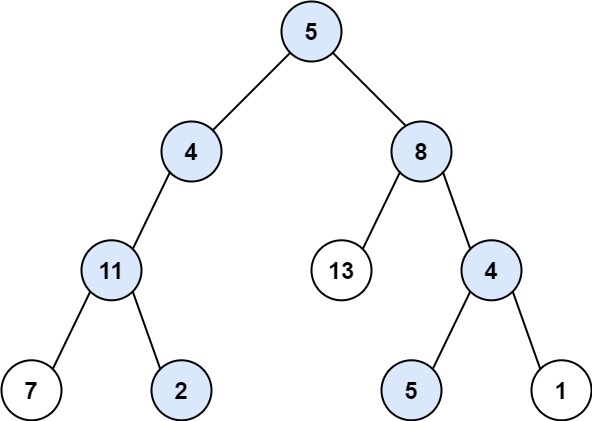
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
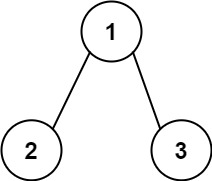
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
题解
路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值!
不放空节点,是为了回溯方便
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if(root == NULL) return ans;
dfs(root, targetSum - root->val);
return ans;
}
// 1.路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值!
void dfs(TreeNode* root, int count) {
// 2.递归终止,找到叶子节点,记录路径
path.push_back(root->val);
if(!root->left && !root->right && count == 0) {
ans.push_back(path);
return;
}
// 3.本层逻辑
if(root->left) { // 不放空节点,是为了回溯方便
dfs(root->left, count - root->left->val);
path.pop_back(); // 递归与回溯是一对
}
if(root->right) {
dfs(root->right, count -root->right->val);
path.pop_back();
}
return;
}
};
三、二叉树的修改与改造
226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
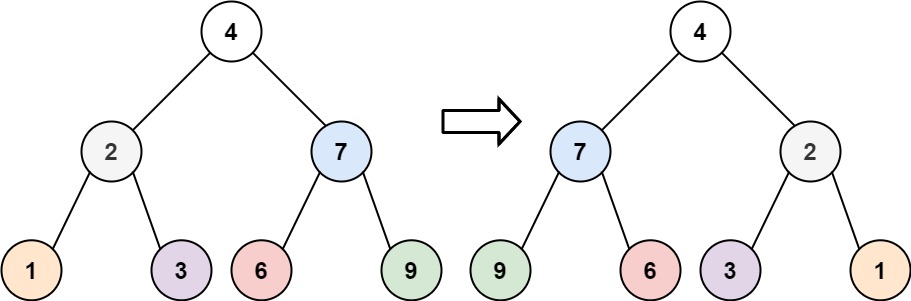
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
题解
遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。
注意只要把每一个节点的左右孩子翻转一下,就可以达到整体翻转的效果
这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历会把某些节点的左右孩子翻转了两次!建议拿纸画一画,就理解了
那么层序遍历可以不可以呢?依然可以的!只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的!
1.深度优先遍历-递归
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == NULL) return NULL;
dfs(root);
return root;
}
// 前序遍历进行翻转
void dfs(TreeNode* root) {
if(root == NULL) return;
// 前序中处理头节点-翻转两个子树
swap(root->left, root->right);
dfs(root->left); dfs(root->right);
}
};
2.深度优先遍历-迭代
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == NULL) return NULL;
stack<TreeNode*> st;
st.push(root);
while(!st.empty()) {
TreeNode* cur = st.top(); st.pop();
swap(cur->left, cur->right);
if(cur->right) st.push(cur->right);
if(cur->left) st.push(cur->left);
}
return root;
}
};
3.广度优先遍历
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == NULL) return NULL;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
while(size-- > 0) {
TreeNode* cur = que.front(); que.pop();
swap(cur->left, cur->right);
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return root;
}
};
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和inorder,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
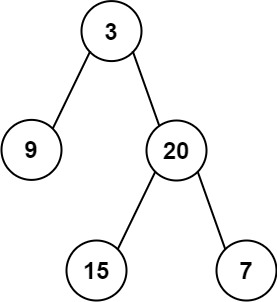
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
题解
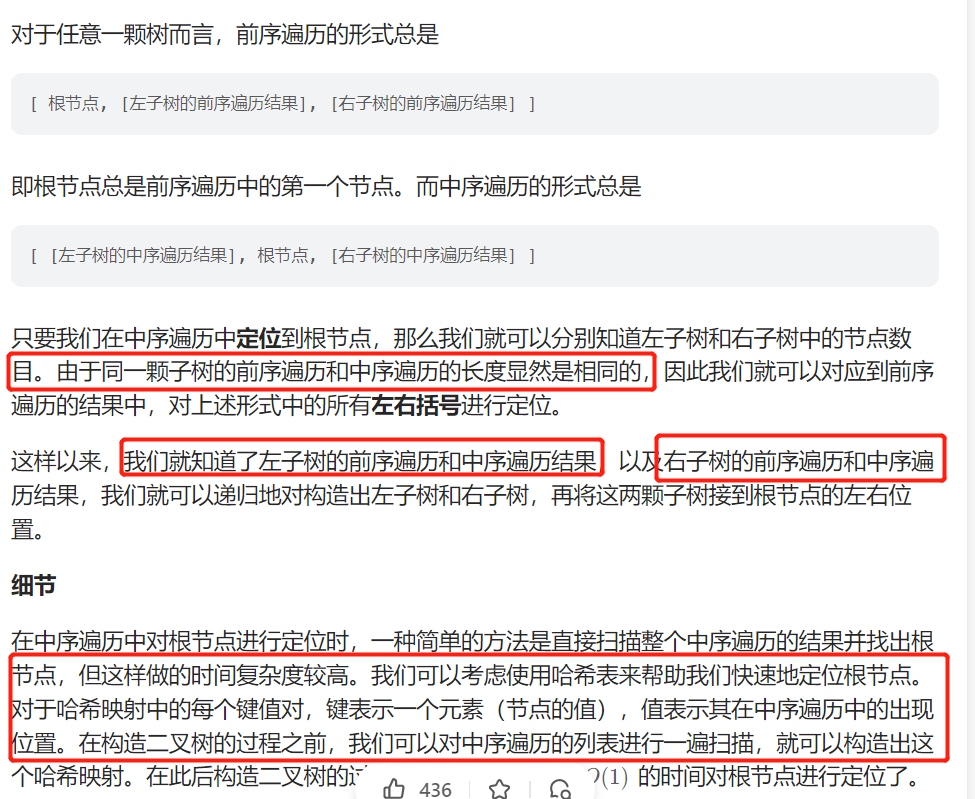
- 前序遍历提供每个根节点的信息,中序遍历提供给定每个根节点的左右子节点信息
- 中序根据根节点,进行左右子树划分
- 左右子树的前序遍历和中序遍历数目一定相同,这样可以分别递归处理左右子树
递归三部曲,
-
递归参数与返回值:左右子树的前序遍历边界和中序遍历的边界(左闭右闭),返回值为根节点
-
终止条件:边界越界,当左右相等时,没有越界
-
逻辑单元是:
- 每层确定一个根节点-由前序遍历的左边界确定(根)
- 确定下层的子节点,
- 根据当前根节点,找到在中序遍历的位置
- 通过中序遍历的位置,划分为左右子树,可以计算左子树数量
- 根据左子树数量,推出左子树的前序遍历边界和后续遍历边界
优化前:每轮需要找根节点位置
class Solution {
int[] preorder, inorder;
public TreeNode buildTree(int[] preorder, int[] inorder) {
this.preorder = preorder;
this.inorder = inorder;
return recur(0, preorder.length - 1, 0, inorder.length - 1);
}
private TreeNode recur(int preL, int preR, int inL, int inR) {
// 终止条件-相等不终止,说明区间有值,要新建根节点
if(preL > preR) return null;
// 逻辑单元
TreeNode root = new TreeNode(preorder[preL]);// 创建节点
// 确定左右子问题-从中序表中找左右子节点个数
int mid = inL; // mid是root在inorder中的位置
while(inorder[mid] != root.val) mid ++;
// inL~mid-1 左子树中序下标,mid + 1~inR 右子树中序下标
int size_left = mid - inL; // 左子树数量
root.left = recur(preL + 1, preL + size_left,inL, mid - 1);
root.right = recur(preL + size_left + 1, preR, mid + 1, inR);
return root;
}
}
优化后:哈希表记录根节点位置
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
this->preorder = preorder;
this->inorder = inorder;
// 1. 先记录中序表中每个值的位置
for(int i = 0; i < preorder.size(); i++) {
map[inorder[i]] = i;
}
// 2. 递归寻找左右子树根节点
return dfs(0, preorder.size() - 1, 0, inorder.size() - 1);
}
TreeNode* dfs(int pre_left, int pre_right, int in_left, int in_right) {
if(pre_left > pre_right) return nullptr;
TreeNode* root = new TreeNode(preorder[pre_left]);
int mid = map[preorder[pre_left]];
int pre_size_left = mid - in_left;
// 构造节点,要将节点连接起来
root->left =
dfs(pre_left + 1, pre_left + pre_size_left, in_left, mid - 1);
root->right =
dfs(pre_left + pre_size_left + 1, pre_right, mid + 1, in_right);
// deleate root;
return root;
}
private:
unordered_map<int, int> map;
vector<int> preorder;
vector<int> inorder;
};
106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
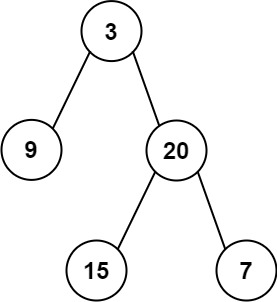
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
-
1 <= inorder.length <= 3000 -
postorder.length == inorder.length -
-3000 <= inorder[i], postorder[i] <= 3000 -
inorder和postorder都由 不同 的值组成 -
postorder中每一个值都在inorder中 -
inorder保证是树的中序遍历 -
postorder保证是树的后序遍历
题解
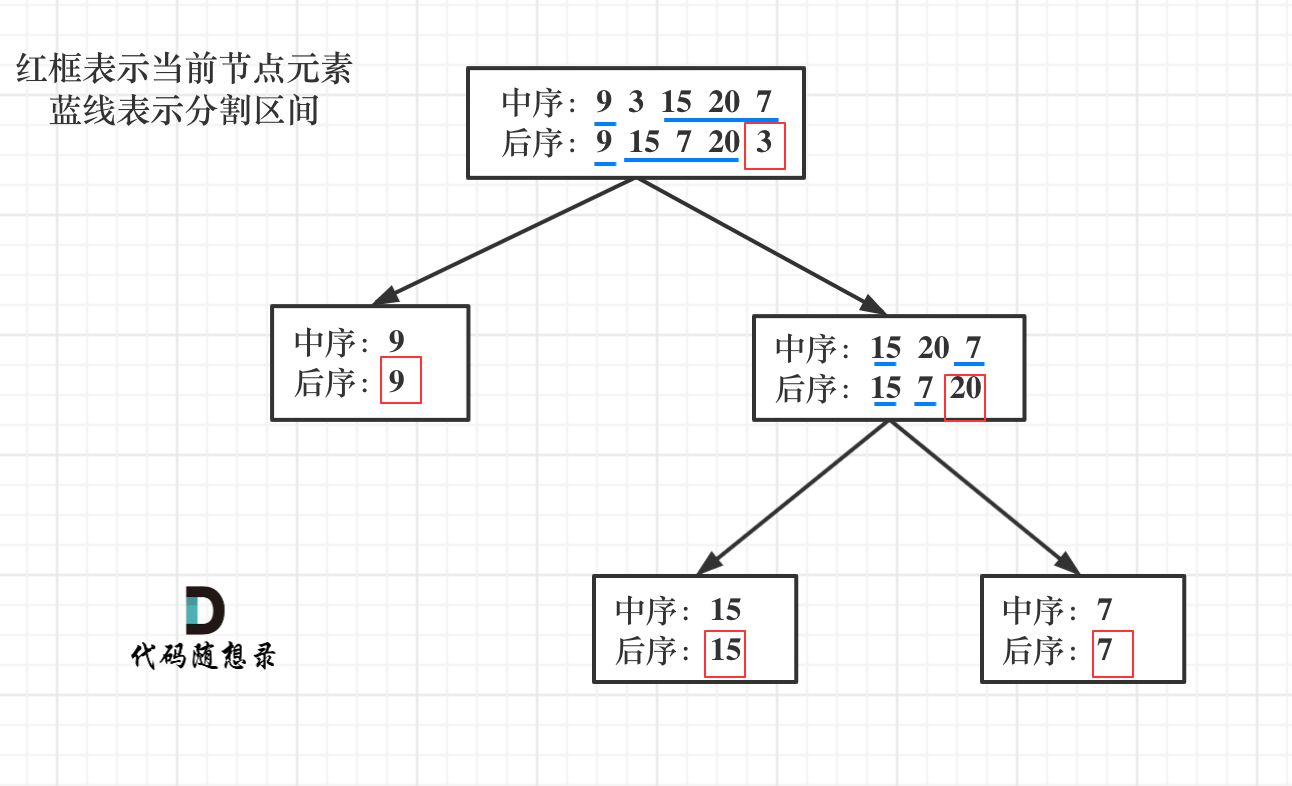
我们可以发现后序遍历的数组最后一个元素代表的即为根节点。
- 知道这个性质后,我们可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标,
- 然后根据其将中序遍历的数组分成左右两部分,左边部分即左子树,右边部分为右子树,
- 针对每个部分可以用同样的方法继续递归下去构造。
流程如图:
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
this->inorder = inorder; this->postorder = postorder;
for(int i = 0; i < inorder.size(); i++) map[inorder[i]] = i;
return dfs(0, inorder.size() -1, 0, postorder.size() - 1);
}
TreeNode* dfs(int in_left, int in_right, int pos_left, int pos_right){
if(in_left > in_right) return nullptr;
TreeNode* root = new TreeNode(postorder[pos_right]);
int mid = map[root->val];
int left_size = mid - in_left;
// 注意边界pos_left + left_size - 1
root->left =
dfs(in_left, mid - 1, pos_left, pos_left + left_size - 1);
root->right =
dfs(mid + 1, in_right, pos_left + left_size, pos_right -1);
return root;
}
private:
unordered_map<int,int> map;
vector<int> inorder;
vector<int> postorder;
};
654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 *最大二叉树* 。
示例 1:
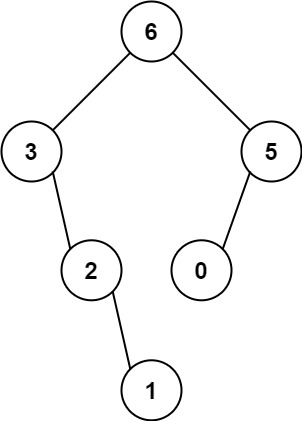
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
示例 2:
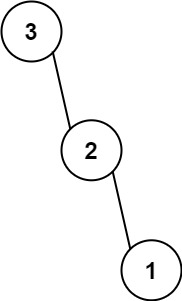
输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000nums中的所有整数 互不相同
题解
构造树一般采用的是前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
class Solution {
public:
vector<int> nums;
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
this->nums = nums;
return dfs(0, nums.size() - 1);
}
// 1. 确定传递参数和返回值
TreeNode* dfs(int left, int right) {
// 2. 终止条件:边界越界
if(left > right) return nullptr;
// 3. 本层逻辑:找到最大值和位置,构建根节点,递归调用左右子树
int maxIndex = left;
for(int i = left + 1; i <= right; i++) {
if(nums[i] > nums[maxIndex]) maxIndex = i;
}
TreeNode* root = new TreeNode(nums[maxIndex]);
root->left = dfs(left, maxIndex - 1);
root->right = dfs(maxIndex + 1, right);
return root;
}
};
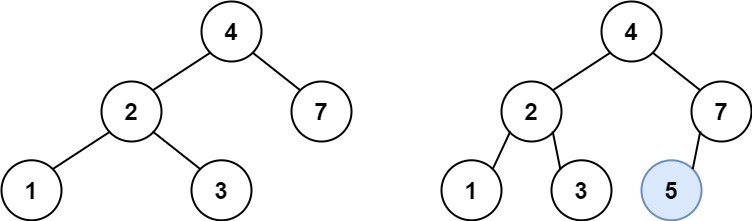
617. 合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
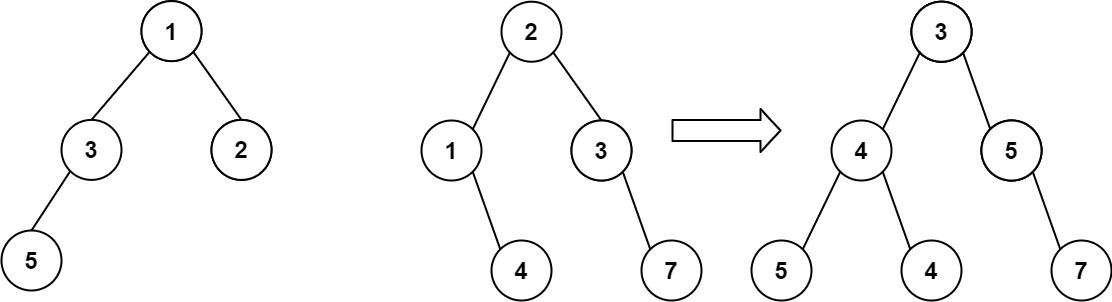
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
提示:
- 两棵树中的节点数目在范围
[0, 2000]内 -104 <= Node.val <= 104
题解
递归
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(!root1) return root2;
if(!root2) return root1;
return dfs(root1, root2);
}
// 1. 返回类型和参数:合并的两个根节点,返回合并的新节点
TreeNode* dfs(TreeNode* t1, TreeNode* t2) {
// 2.边界,遇到空节点
if(!t1) return t2;
if(!t2) return t1;
// 3.本层逻辑:两个根都不为空,合并成新节点,再继续递归下去
TreeNode* root = new TreeNode(t1->val + t2->val);
root->left = dfs(t1->left, t2->left);
root->right = dfs(t1->right, t2->right);
return root;
}
};
迭代
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2;
if (t2 == NULL) return t1;
queue<TreeNode*> que;
que.push(t1);
que.push(t2);
while(!que.empty()) {
TreeNode* node1 = que.front(); que.pop();
TreeNode* node2 = que.front(); que.pop();
// 此时两个节点一定不为空,val相加
node1->val += node2->val;
// 如果两棵树左节点都不为空,加入队列
if (node1->left != NULL && node2->left != NULL) {
que.push(node1->left);
que.push(node2->left);
}
// 如果两棵树右节点都不为空,加入队列
if (node1->right != NULL && node2->right != NULL) {
que.push(node1->right);
que.push(node2->right);
}
// 当t1的左节点 为空 t2左节点不为空,就赋值过去
if (node1->left == NULL && node2->left != NULL) {
node1->left = node2->left;
}
// 当t1的右节点 为空 t2右节点不为空,就赋值过去
if (node1->right == NULL && node2->right != NULL) {
node1->right = node2->right;
}
}
return t1;
}
};
四、二叉搜索树的属性
700. 二叉搜索树中的搜索
\700. 二叉搜索树中的搜索
简单
355
相关企业
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
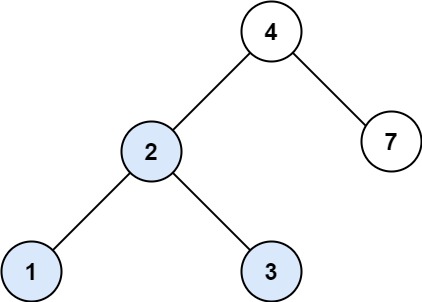
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
示例 2:
输入:root = [4,2,7,1,3], val = 5
输出:[]
提示:
- 数中节点数在
[1, 5000]范围内 1 <= Node.val <= 107root是二叉搜索树1 <= val <= 107
题解
- 二叉搜索树,节点有序,因此遍历时,可以选择左右分支,提高效率
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if(root == nullptr) return nullptr;
if(root->val == val) return root;
else if(root->val < val) return searchBST(root->right, val);
else return searchBST(root->left, val);
}
};
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
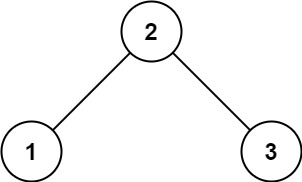
输入:root = [2,1,3]
输出:true
示例 2:
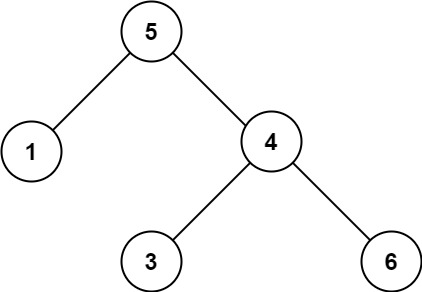
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 104]内 -231 <= Node.val <= 231 - 1
题解1:中序遍历有序
这道题目比较容易陷入两个陷阱:
陷阱1
-
不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了。
-
局部满足,整体可能不满足
写出了类似这样的代码:
if (root->val > root->left->val && root->val < root->right->val) {
return true;
} else {
return false;
}
我们要比较的是 左子树所有节点小于中间节点,右子树所有节点大于中间节点。所以以上代码的判断逻辑是错误的。
例如: [10,5,15,null,null,6,20] 这个case:
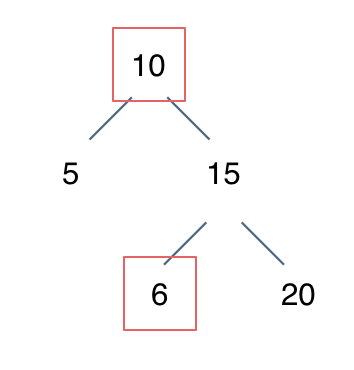
节点10大于左节点5,小于右节点15,但右子树里出现了一个6 这就不符合了!
陷阱2
样例中最小节点 可能是int的最小值,如果这样使用最小的int来比较也是不行的。
此时可以初始化比较元素为longlong的最小值。
class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // 将二叉搜索树转换为有序数组
traversal(root->right);
}
public:
bool isValidBST(TreeNode* root) {
vec.clear(); // 不加这句在leetcode上也可以过,但最好加上
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// 注意要小于等于,搜索树里不能有相同元素
if (vec[i] <= vec[i - 1]) return false;
}
return true;
}
};
题解2:递归-不适用额外数组,递归中进行判断
注意两个陷阱
-
1.不能单纯的比较左节点小于中间节点,右节点大于中间节点就完事了。
-
2.样例中最小节点 可能是int的最小值,如果这样使用最小的int来比较也是不行的。
-
解决1:开Long空间,找比int更小的数来比较
-
如果测试数据中有 longlong的最小值,怎么办?
不可能在初始化一个更小的值了吧。 建议避免 初始化最小值,如下方法取到最左面节点的数值来比较。
-
-
解决2:创建节点比较,最小的int值不去比较(最小的值一定在中序遍历第一个位置),直接跳过,赋值就行
-
class Solution {
TreeNode max;
public boolean isValidBST(TreeNode root) {
if(root == null) return false;
return dfs(root);
}
private boolean dfs(TreeNode root) {
if(root == null) return true;
boolean left = dfs(root.left);
// 二叉树最小数可能是边界,但max为null
if(max != null && root.val <= max.val) return false;
max = root; // 每次更新max,保证单调性
boolean right = dfs(root.right);
return left && right;
}
}
class Solution {
public:
TreeNode* pre;
bool isValidBST(TreeNode* root) {
if(!root) return true;
bool left = isValidBST(root->left);
if(pre && pre->val >= root->val) return false;
pre = root;
bool right = isValidBST(root->right);
return left && right;
}
};
530. 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:
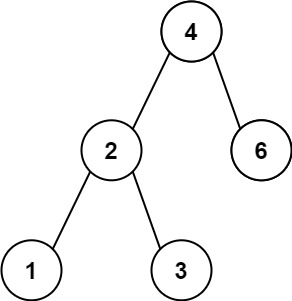
输入:root = [4,2,6,1,3]
输出:1
示例 2:
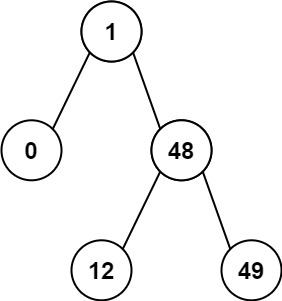
输入:root = [1,0,48,null,null,12,49]
输出:1
提示:
- 树中节点的数目范围是
[2, 104] 0 <= Node.val <= 105
**注意:**本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同
题解
题目中要求在二叉搜索树上任意两节点的差的绝对值的最小值。
注意是二叉搜索树,二叉搜索树可是有序的。
遇到在二叉搜索树上求什么最值啊,差值之类的,就把它想成在一个有序数组上求最值,求差值,这样就简单多了。
解法1:先转为有序数组
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> vec;
int getMinimumDifference(TreeNode* root) {
dfs(root);
int ans = INT_MAX;
for(int i = 1; i < vec.size(); i++) {
ans = min(ans, vec[i] - vec[i - 1]);
}
return ans;
}
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root->left);
vec.push_back(root->val);
dfs(root->right);
}
};
解法2:直接在中序递归遍历中处理
需要用一个pre节点记录一下cur节点的前一个节点。
如图:
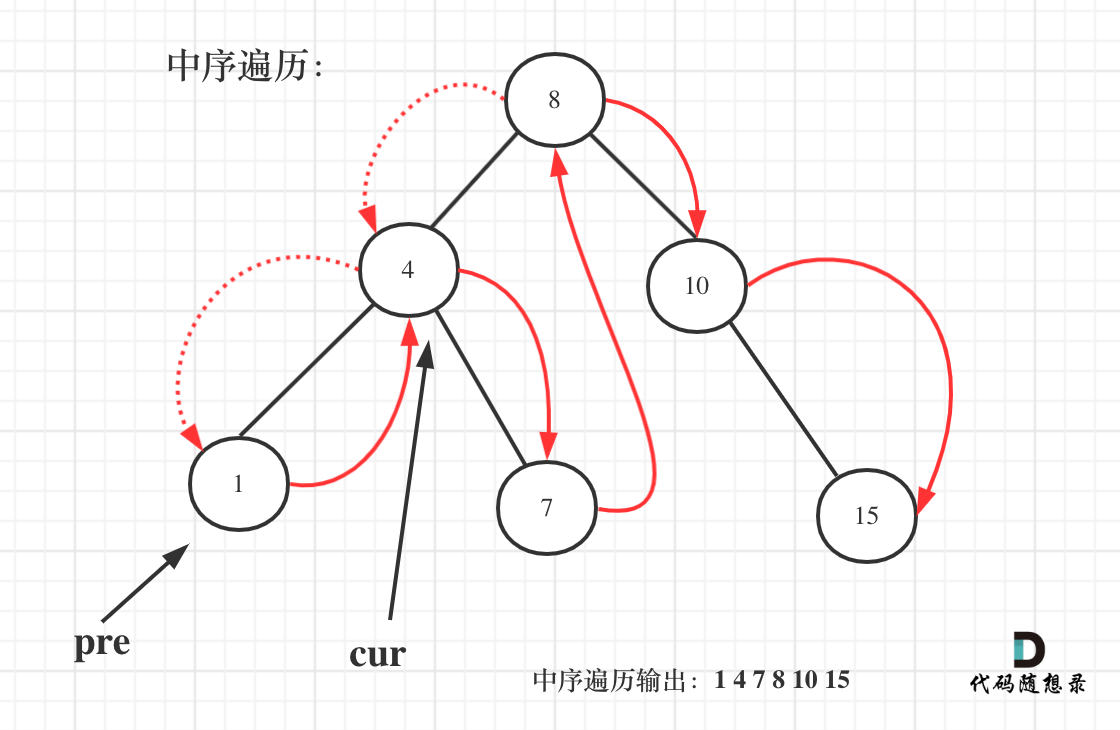
class Solution {
public:
int ans = INT_MAX;
TreeNode* pre = nullptr;
int getMinimumDifference(TreeNode* root) {
dfs(root);
return ans;
}
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root->left);
if(pre) ans = min(ans, root->val - pre->val);
pre = root;
dfs(root->right);
}
};
解法3:迭代法
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL;
int result = INT_MAX;
while (cur != NULL || !st.empty()) {
if (cur != NULL) { // 指针来访问节点,访问到最底层
st.push(cur); // 将访问的节点放进栈
cur = cur->left; // 左
} else {
cur = st.top();
st.pop();
if (pre != NULL) { // 中
result = min(result, cur->val - pre->val);
}
pre = cur;
cur = cur->right; // 右
}
}
return result;
}
};
501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
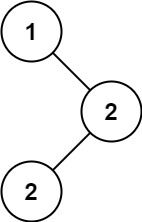
输入:root = [1,null,2,2]
输出:[2]
示例 2:
输入:root = [0]
输出:[0]
提示:
- 树中节点的数目在范围
[1, 104]内 -105 <= Node.val <= 105
**进阶:**你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
题解
解法1:普通二叉树解法
如果不是二叉搜索树,最直观的方法一定是把这个树都遍历了,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
C++中如果使用std::map或者std::multimap可以对key排序,但不能对value排序。
所以要把map转化数组即vector,再进行排序,当然vector里面放的也是pair<int, int>类型的数据,第一个int为元素,第二个int为出现频率。
class Solution {
private:
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历
if (cur == NULL) return ;
map[cur->val]++; // 统计元素频率
searchBST(cur->left, map);
searchBST(cur->right, map);
return ;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second;
}
public:
vector<int> findMode(TreeNode* root) {
unordered_map<int, int> map; // key:元素,value:出现频率
vector<int> result;
if (root == NULL) return result;
searchBST(root, map);
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序
result.push_back(vec[0].first); // 排序后,最前面的就是频率最大
for (int i = 1; i < vec.size(); i++) {
// 取最高的放到result数组中-寻找与最大频率相等的数
if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
else break;
}
return result;
}
};
解法2:中序遍历有序-处理有序数列

然后,我们考虑不存储这个中序遍历序列。 如果我们在递归进行中序遍历的过程中,访问当了某个点的时候直接使用上面的 update 函数,就可以省去中序遍历序列的空间
class Solution {
public:
vector<int> ans;
int pre, cnt, maxCnt;
vector<int> findMode(TreeNode* root) {
if(root == nullptr) return ans;
dfs(root);
return ans;
}
void dfs(TreeNode* root) {
if(root == nullptr) return;
dfs(root->left);
update(root->val); // 更新最大频率并记录数-如果数值会越界,就传节点
dfs(root->right);
}
void update(int cur) {
// 1. 先更新pre和cnt
if(pre == cur) cnt++;
else {
cnt = 1; // 复位,更新pre
pre = cur;
}
// 2. 更新maxCnt和答案,可以每次先加入ans,maxCnt更新后,再清空更新ans
if(cnt == maxCnt) ans.push_back(cur);
if(cnt > maxCnt) {
maxCnt = cnt;
ans.clear();
ans.push_back(cur);
}
}
};
五、二叉树公共祖先问题
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
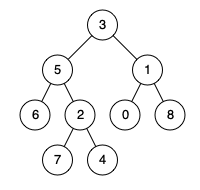
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
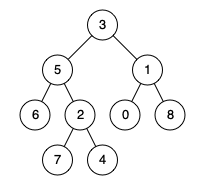
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围
[2, 105]内。 -109 <= Node.val <= 109- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
题解
- 使用递归回溯算法,向上标记法
- P一直向上找父节点,并标记,q向上标记,遇到第一个标记点,即是最近公关祖先
- 实际题中给出的都是子节点,因此,此逻辑需要转换
- 因所有节点不相同,只要在子树中找到p或q,都可以向上标记,可以不必区分到底是p还是q
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == p || root == q || root == NULL) return root;
// 先深度递归,接收子树的状态
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
// 遍历到最深处,一级级向上回溯,第一次左右都不为null的,即都找到的就是答案
// 后续遍历,处理完子树后,向上回溯判断父节点
if(left && right) return root; // 第一次找到的答案
// 左没有,就向上回溯右,题中保证有,找到右了,就一定是右,右也为null,就回溯null
if(!left) return right;
return left;
}
};
- 解法2:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
TreeNode p, q, ans;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
this.p = p;
this.q = q;
recur(root);
return ans;
}
private Pair<Boolean, Boolean> recur(TreeNode root) {
if(root == null) return new Pair<Boolean, Boolean>(false, false);
// 先深度递归,自底向上汇总结果
Pair<Boolean, Boolean> leftRes = recur(root.left);
Pair<Boolean, Boolean> rightRes = recur(root.right);
// 递归到最深处,处理当前逻辑
boolean key = leftRes.getKey() || rightRes.getKey() || root == p;
boolean value = leftRes.getValue() || rightRes.getValue() || root == q;
Pair<Boolean, Boolean> res = new Pair(key, value);
if(key && value && ans == null) ans = root;
return res;
}
}
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
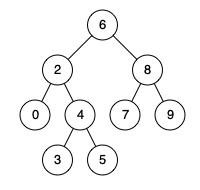
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
题解
因为是有序树,所有 如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。
那么只要从上到下去遍历,遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是q 和 p的公共祖先。因为如果继续往左走,会错过成为q的祖先,继续往右走,会错过成为p的祖先。
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[p, q]区间中,即 节点5,此时可以说明 p 和 q 一定分别存在于 节点 5的左子树,和右子树中。
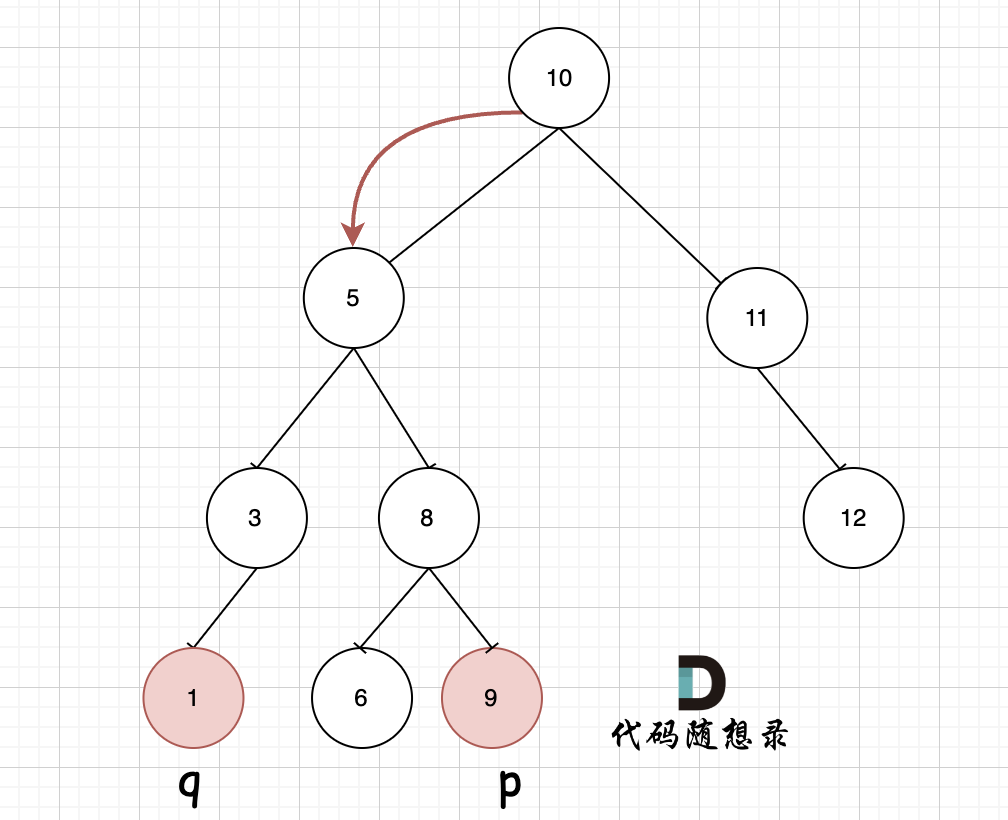
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为q的祖先, 如果从节点5继续向右遍历则错过成为p的祖先。
class Solution {
public:
// 类似二分查找,寻找在[p, q]之间的节点
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root->val > p->val && root->val > q->val) { // 往左找
return lowestCommonAncestor(root->left, p, q);
} else if(root->val < p->val && root->val < q->val) { // 往右找
return lowestCommonAncestor(root->right, p, q);
} else return root; // 直到第一次找到中间节点
}
};
六、二叉搜索树的修改与改造
701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
题解
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root) return new TreeNode(val); // 找到插入位置,新建节点插入
if(val < root->val) { // 往左子树里插入
root->left = insertIntoBST(root->left, val);
} else if(val > root->val) { // 往右子树里插入
root->right = insertIntoBST(root->right, val);
}
// 如果相等,什么都不做,直接返回(保证二叉树中元素均不同)
return root;
}
};
450. 删除二叉搜索树中的节点
\450. 删除二叉搜索树中的节点
中等
1K
相关企业
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
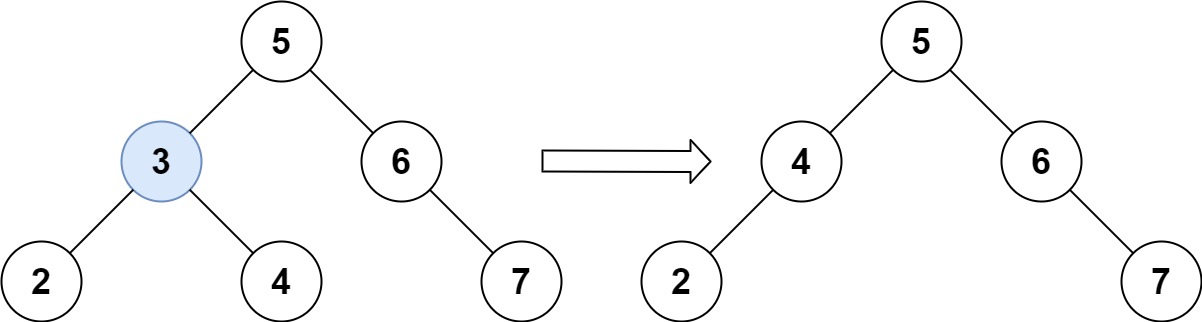
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
题解


- 1.先检索查询到指定节点
- dfs找指定删除节点(前序,中序、后序都可以)
- 2.判断节点的左右子节点
- 如果只有一个子节点,或没有子节点,只需将剩下的子节点替代指定节点即可
- 如果左右子树都有,需要找到中序后继节点或前序节点
- 找到后,将后继节点从二叉树结构中删除
- 然后用后继节点的值代替指定节点的值,完成替换
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
// 1. 终止条件:空节点直接返回
if(!root) return nullptr;
// 2.dfs遍历,先找到要删除的节点
if(root->val == key) { // 找到了,开始处理删除工作
// 1. 先找到后继节点
// 如果左分支为空,将右分支替换成当前节点返回给上级
if(!root->left) return root->right;
if(!root->right) return root->left;
// 如果左右都不为空,找右后继节点,或左前序节点,都是满足顺序的
// 右后继节点->右支树中的最小值,比右分支其他数都小,比左分支都大
TreeNode* successor = root->right;
while(successor->left) successor = successor->left;
// 2. 删除后继节点-可递归删除,免得开map记录父节点
root->right = deleteNode(root->right, successor->val);//要连上
// 3. 用后继节点替换要删除的节点
root->val = successor->val; //root左右指向已经处理好了
return root;
} else if(root->val > key) { // 往左寻找
root->left = deleteNode(root->left, key); // 要连接上
} else { // 往右寻找
root->right = deleteNode(root->right, key);
}
return root;
}
};
669. 修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
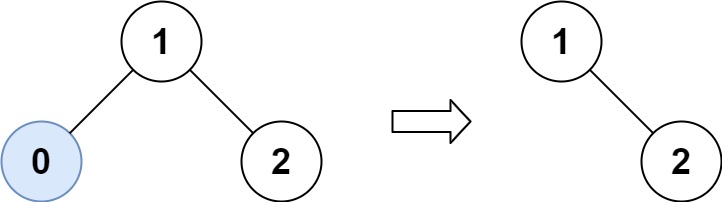
输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]
示例 2:
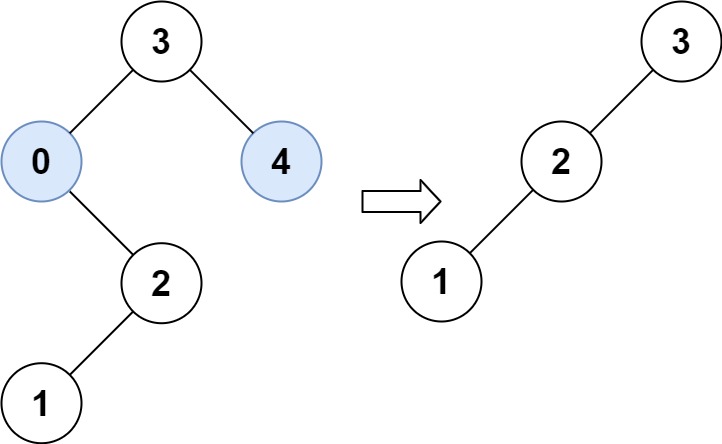
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
题解
-
思路1:可以深度遍历每个节点进行判断,如果不满足,就删除节点,调用450题删除节点的逻辑,这是这样复杂度比较高,且,有大量可以剪枝的处理
-
思路2:直接深度dfs处理节点-进行剪枝处理-直接砍掉一个分支
- 注意节点传递问题:当前逻辑的根节点不合法后,父节点没有记录,先不做连接,返回下层递归结果,下层递归处理找到合法节点后,再返回给上级,当前节点的父节点就连上了孙子节点
- 因此,需要在节点合法的逻辑中,进行节点的连接与返回

class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root) return nullptr;
if(root->val < low) { // 左子树都砍掉,右子树替换当前节点
// 当前逻辑,父节点没记录,先不连接,返回,交给上级去处理
return trimBST(root->right, low, high);//寻找符合区间[low, high]的节点
} else if(root->val > high) {
return trimBST(root->left, low, high);
} else { // 节点满足,可以做父节点,去连接子节点返回的值
root->left = trimBST(root->left, low, high);//接入符合条件的左孩子
root->right = trimBST(root->right, low, high);//接入符合条件的右孩子
return root; // 将合法的节点返回给上级
}
}
};
108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
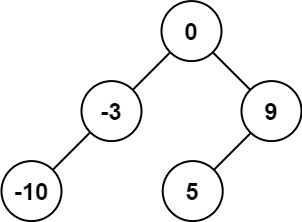
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
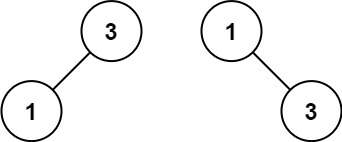
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
题解
本题其实要比二叉树:构造二叉树登场! (opens new window)和 二叉树:构造一棵最大的二叉树 (opens new window)简单一些,因为有序数组构造二叉搜索树,寻找分割点就比较容易了。
分割点就是数组中间位置的节点。
那么为问题来了,如果数组长度为偶数,中间节点有两个,取哪一个?
取哪一个都可以,只不过构成了不同的平衡二叉搜索树。
class Solution {
public:
vector<int> nums;
TreeNode* sortedArrayToBST(vector<int>& nums) {
this->nums = nums;
return dfs(0, nums.size() - 1);
}
TreeNode* dfs(int left, int right) {
if(left > right) return nullptr;
int mid = (left + right) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = dfs(left, mid - 1);
root->right = dfs(mid + 1, right);
return root;
}
};
538. 把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
**注意:**本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
示例 1:
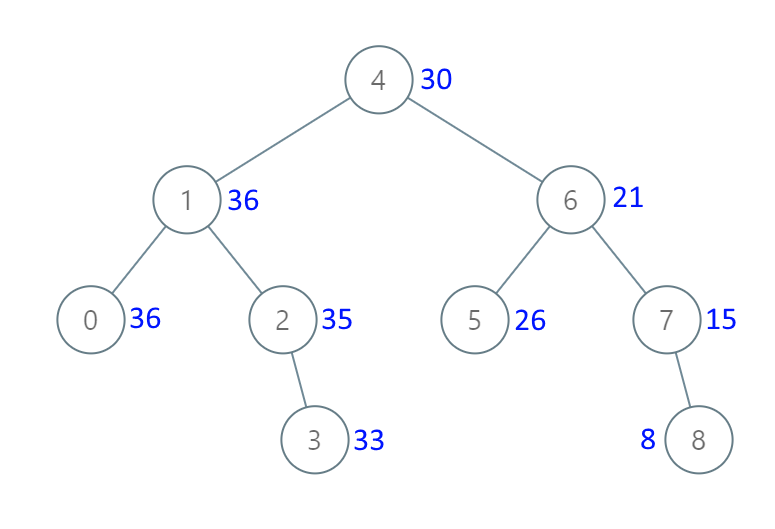
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
题解
其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。
那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加就可以了。
class Solution {
public:
int preSum = 0;
TreeNode* convertBST(TreeNode* root) {
if(!root) return nullptr;
convertBST(root->right); // 右-只需改变节点值,指向无需更改
preSum += root->val;
root->val = preSum;
convertBST(root->left); // 左
return root;
}
};