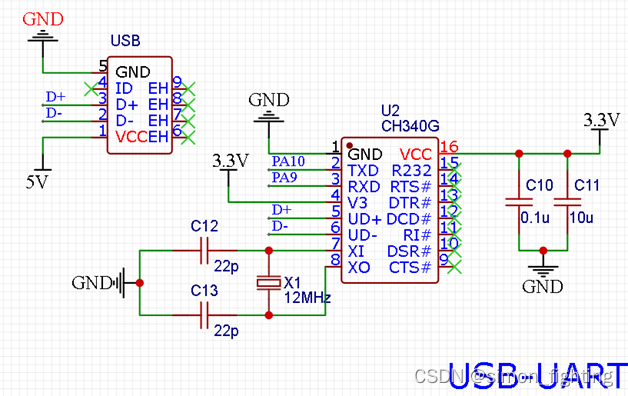
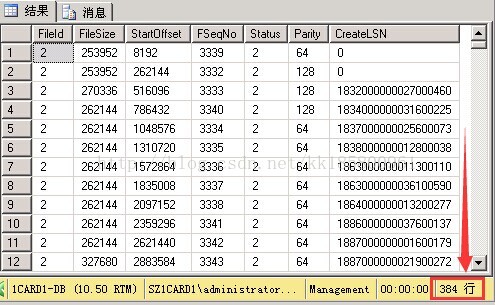
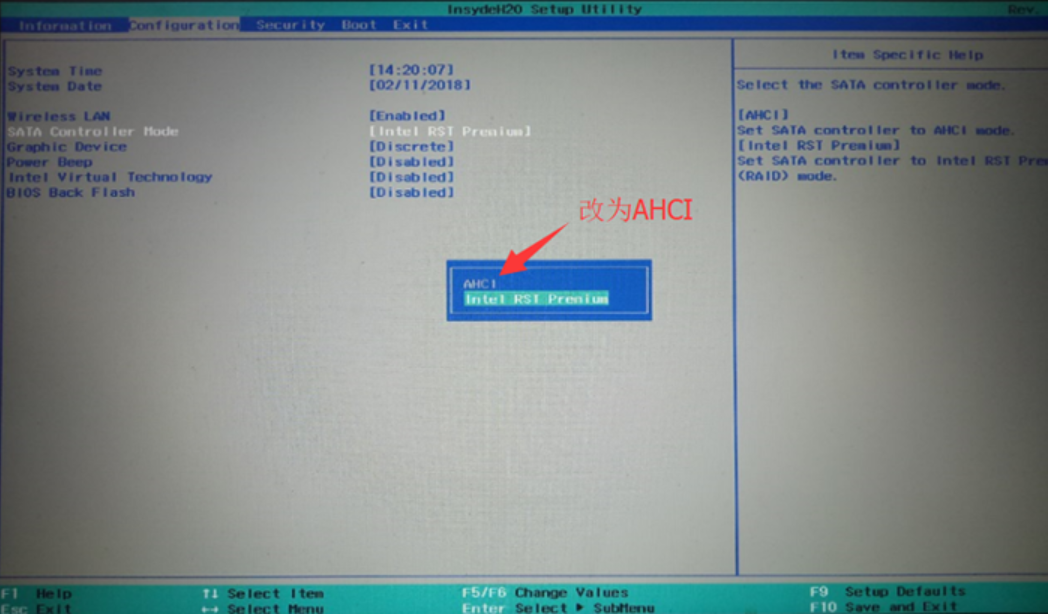
在较大阶跃响应时,很容易产生超调。采用步进式积分分离PID控制,该方法不直接对阶跃信号进行响应,而是使输入指令信号一步一步地逼近所要求的阶跃信号,可使对象运行平稳,适用于高精度伺服系统的位置跟踪。
在步进式PID控制的仿真中,取位置指令为R=20,实际输入指令yd(k)采用0.25的步长变化,逐渐逼近输入指令信号R。仿真结果表明,采用积分分离式PID .控制,响应速度快,但阶跃响应不平稳,需要的控制输入信号大;而采用步进式PID 控制,虽然响应速度慢,但阶跃响应平稳,需要的控制输入信号小,具有很好的工程实用价值。
仿真实例:
被控对象为:
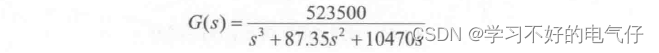
采样时间为1ms,输入指令信号为R=20。采用本控制算法进行阶跃响应。其中 M=1时为积分分离式 PID控制,响应结果,如图1所示;M=2时为步进式积分分离PID控制,响应结果及输入信号的变化如图2和图3。
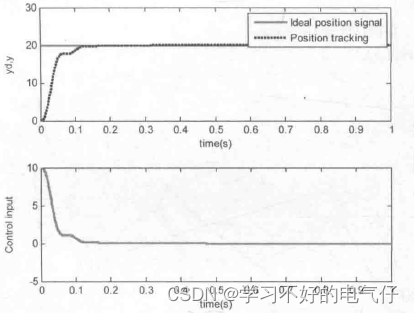
图1 积分分离阶跃响应(M=1)
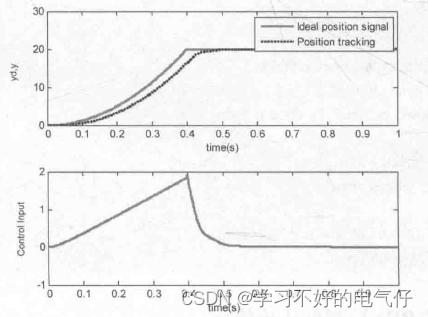
图2 步进式积分分离阶跃响应和控制输入(M=2)
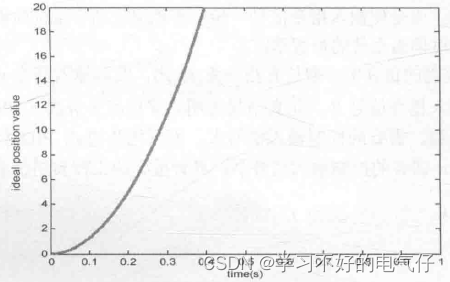
图3 步进式阶跃信号yd(k)的变化
仿真程序:
%PID Control with Gradual approaching input value
clear all;
close all;
ts=0.001;
sys=tf(5.235e005,[1,87.35,1.047e004,0D);dsys=c2d(sys,ts,z);
[num,den]-tfdata(dsys,'v');
u_I=0;u_2=0;u_3=0;u_4=0;u_5=0;y_1=0;y_2=0;y_3=0;
error_1=0;error_2=0;ei=0;
kp=0.50;ki=0.05;
rate=0.25;
ydi=0.0;
for k=1:1:1000
time(k)-k*ts;
R=20; %Step Signal
%Linear model
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_l+num(3)*u_2+num(4)*u_3;
M=2;
if M==1 %Using simple PID
yd(k)=R;
error(k)=yd(k)-y(k);
end
if M==2 %Using Gradual approaching input value
if ydi<R-0.25
ydi=ydi+k*ts*rate;elseif ydi>R+0.25
ydi=ydi-k*ts*rate;
else
ydi=R;
end
yd(k)=ydi;
error(k)=yd(k)-y(k);
end
%PID with I separation
if abs(error(k))<=0.8
ci=eiterror(k)*ts;
else
ei=0;end
u(k)=kp*error(k)+ki*ei;
%--------Return of PID parameters--------------%
yd_1=yd(k);
u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y 1=y(k);
error_2=crror_1:
error_1=error(k);end
figure(1);subplot(211);
plot(time,yd,'r',time,y,'k:', linewidth' ,2);xlabel("'time(s);ylabel('yd,y);
legend(Ideal position signal'.,'Position tracking');subplot(212);
plot(time.u,r,linewidth',2);
xlabel('time(s));ylabel('Control input');figure(2);
plot(time,yd,'r,linewidth',2);
xlabel("'time(s)'):ylabel('ideal position value');