半导体产业链掀起涨价潮,先进封装迎接利好。
这里我们来聊国内先进封装企业——晶方科技。

近期,由于产能供不应求,台积电决定上调先进封装产品价格,还表示订单已经排到2026年。

大哥吃不下了,剩下的订单全都是空间。
与半导体产业大部分公司一样,晶方科技去年业绩承压、今年一季度反转,其中净利润更是同比增长72.37%。

利润大增的秘诀在于遥遥领先行业的利润率,2024年Q1,晶方科技毛利率接近40%,
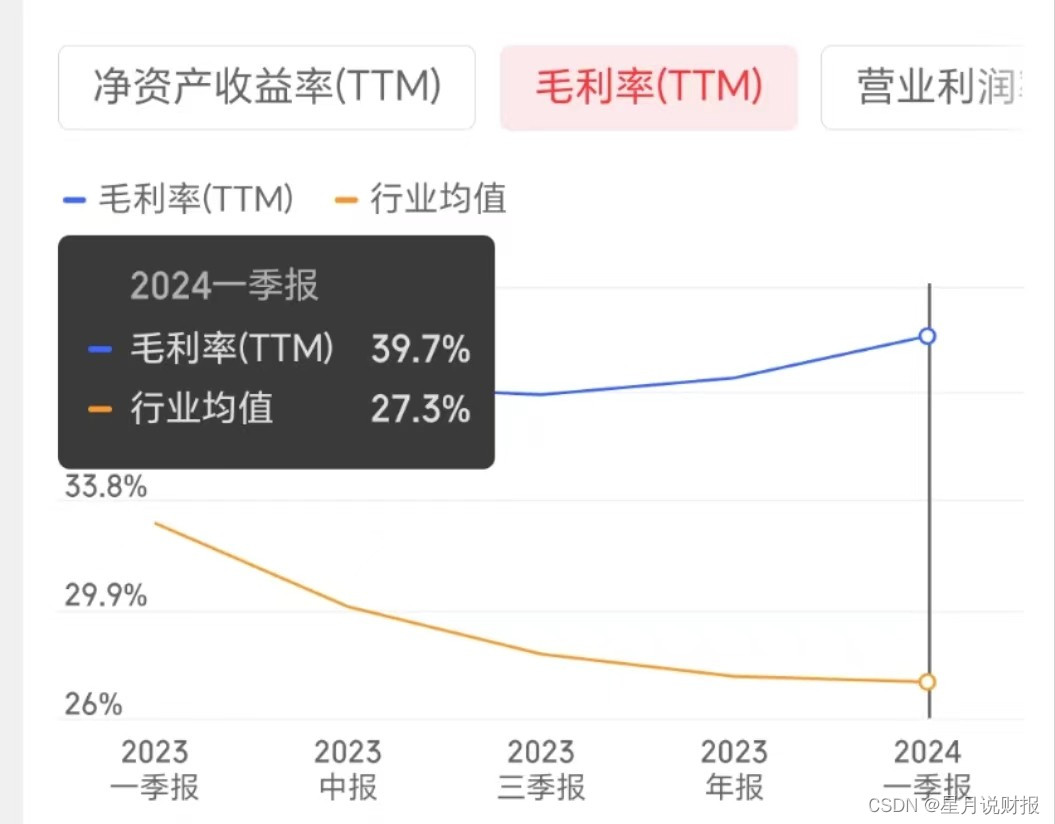
对比行业里长电科技、通富微电、华天科技,毛利率基本维持在10-20%上下波动,可以说领先行业。
一方面是产品差异化竞争优势明显。对比传统封装,先进封装芯片系统内存宽带和性能更高,但相应能耗比和成本也会更高。简单来说就是更贵更强更好。它的技术要求和壁垒都比较高,不是所有人都能分一杯羹,而晶方科技的核心技术TSV(硅通孔技术)是半导体先进封装(最)核心的技术之一,

手握金刚钻,自然不缺瓷器活。
另一方面CIS(图像传感器)芯片封测需求广泛。晶方科技作为全球(最)大的CIS芯片封测厂商,华为、格科微、韦尔股份等都是它重要“金主爸爸”。无论是智能手机摄像头数量提升,

还是智能驾驶带来的车载摄像头增量,都能给CIS芯片市场带来了巨大的增长机遇。
不过值得注意的是,受投资收益影响,公司净现金流1.06亿,较去年同期为8.20亿大幅下降,现金流短期内存在压力;此外,近年来海外营收占比持续增长,超过70%,也存在一定的安全风险。

不过作为阿斯麦的光学器件供应商,未来在光刻机的国产替代战略中,可能也会带来想象空间。