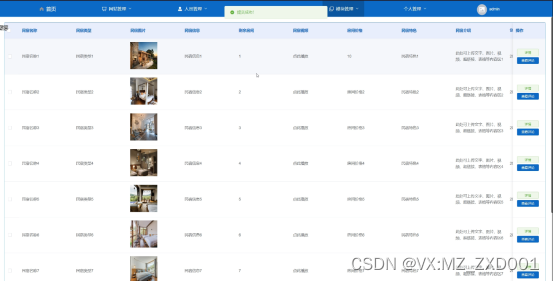
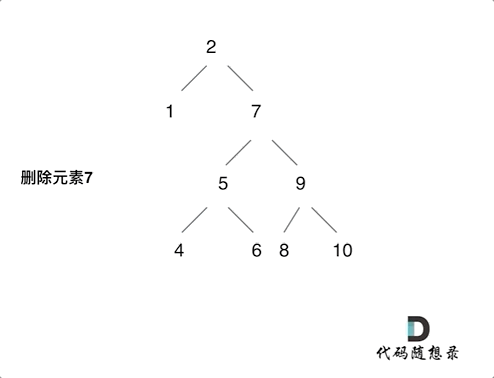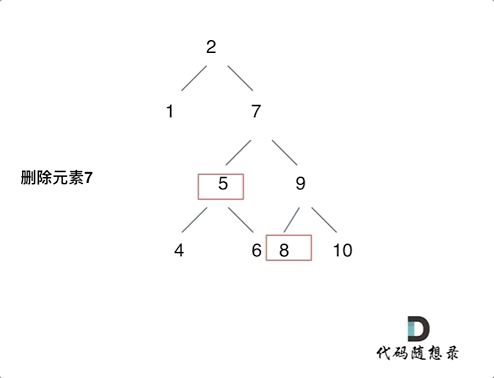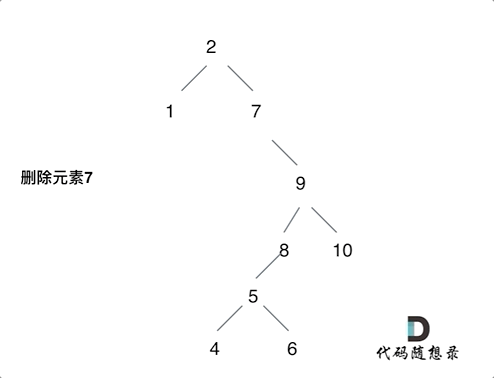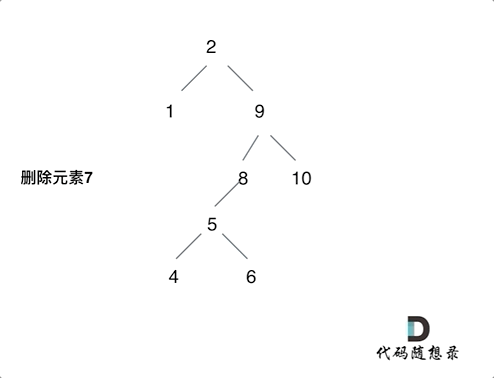
最佳平方逼近
函数逼近是使用一种简单易算的函数来近似表示一个复杂函数。

该问题可转化为求解线性方程组
G n C = F n G_{n}C=F_{n} GnC=Fn
其中,系数 C = ( c 0 , c 1 , ⋯ , c n ) T , F n = ( ( f , φ 0 ) , ( f , φ 1 ) , ⋯ , ( f , φ n ) ) T C=(c_{0},c_{1},\cdots,c_{n})^{\mathrm{T}},F_{n}=((f,\varphi_{0}),(f,\varphi_{1}),\cdots,(f,\varphi_{n}))^{\mathrm{T}} C=(c0,c1,⋯,cn)T,Fn=((f,φ0),(f,φ1),⋯,(f,φn))T
G n G_n Gn是格拉姆矩阵。称该线性方程组为法方程组或正规方程组。
最佳平方逼近的解函数为 φ ∗ = ∑ i = 0 n c i ∗ φ i \varphi^*=\sum_{i=0}^nc_i^*\varphi_i φ∗=∑i=0nci∗φi。
最佳平方逼近函数,继承内积,即 ( φ ∗ , φ ∗ ) = ( φ ∗ , f ) (\varphi^*,\varphi^*)=(\varphi^*,f) (φ∗,φ∗)=(φ∗,f)。
取逼近区间[a,b]为[0,1]时,其平方误差为:
∥
φ
∗
−
f
∥
2
2
=
(
f
,
f
)
−
F
n
T
C
∗
=
∫
0
1
f
2
(
x
)
d
x
−
F
n
T
C
∗
.
\parallel\varphi^*-f\parallel_2^2=(f,f)-F_n^\mathrm{T}C^*=\int_0^1f^2(x) \mathrm{d}x-F_n^\mathrm{T} C^* .
∥φ∗−f∥22=(f,f)−FnTC∗=∫01f2(x)dx−FnTC∗.

正交系
内积空间
V
V
V上的两个元素
f
f
f和
g
g
g,如果有内积
(
f
,
g
)
=
0
(f,g)=0
(f,g)=0,则称
f
f
f和
g
g
g关于内积
(
⋅
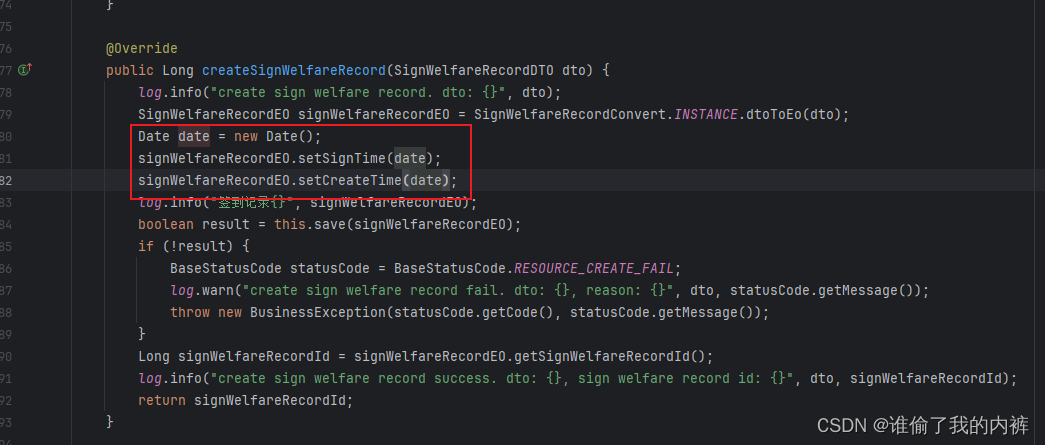
,
⋅
)
(\cdot,\cdot)
(⋅,⋅)正交。若内积空间上的元素系
{
f
i
}
\{f_{i}\}
{fi}满足两两正交
{
(
f
i
,
f
j
)
=
0
(
i
≠
j
)
,
(
f
i
,
f
i
)
=
γ
i
>
0
,
\begin{cases}(f_i,f_j)=0\quad(i\neq j) ,\\(f_i,f_i)=\gamma_i>0 ,\end{cases}
{(fi,fj)=0(i=j),(fi,fi)=γi>0,
则称
{
f
i
}
\{f_{i}\}
{fi}为正交系,若有
(
f
i
,
f
i
)
=
1
(
i
=
0
,
1
,
2
,
3...
)
(f_i,f_i)=1(i=0,1,2,3...)
(fi,fi)=1(i=0,1,2,3...),则称
{
f
i
}
\{f_{i}\}
{fi}为标准正交系。
给定一组正交基,法方程组系数矩阵
G
n
G_n
Gn为对角矩阵,其解向量为:
C
∗
=
(
(
φ
0
,
f
)
(
φ
0
,
φ
0
)
,
(
φ
1
,
f
)
(
φ
1
,
φ
1
)
,
⋯
,
(
φ
n
,
f
)
(
φ
n
,
φ
n
)
)
T
.
C^* = \left(\frac{(\varphi_0,f)}{(\varphi_0,\varphi_0)},\frac{(\varphi_1,f)}{(\varphi_1,\varphi_1)},\cdots,\frac{(\varphi_n,f)}{(\varphi_n,\varphi_n)}\right)^\mathrm{T}.
C∗=((φ0,φ0)(φ0,f),(φ1,φ1)(φ1,f),⋯,(φn,φn)(φn,f))T.
函数
f
(
x
)
f(x)
f(x)的最佳平方逼近函数为
φ
∗
=
(
φ
0
,
f
)
(
φ
0
,
φ
0
)
φ
0
+
(
φ
1
,
f
)
(
φ
1
,
φ
1
)
φ
1
+
⋯
+
(
φ
n
,
f
)
(
φ
n
,
φ
n
)
φ
n
.
\varphi^*=\frac{(\varphi_0,f)}{(\varphi_0,\varphi_0)}\varphi_0+\frac{(\varphi_1,f)}{(\varphi_1,\varphi_1)}\varphi_1+\cdots+\frac{(\varphi_n,f)}{(\varphi_n,\varphi_n)}\varphi_n.
φ∗=(φ0,φ0)(φ0,f)φ0+(φ1,φ1)(φ1,f)φ1+⋯+(φn,φn)(φn,f)φn.
平方误差为
∥
f
−
φ
∗
∥
2
2
=
(
f
,
f
)
−
∑
i
=
0
n
(
f
,
φ
i
)
2
(
φ
i
,
φ
i
)
.
\parallel f-\varphi^*\parallel_2^2=(f,f)-\sum_{i=0}^n\frac{(f,\varphi_i)^2}{(\varphi_i,\varphi_i)}.
∥f−φ∗∥22=(f,f)−i=0∑n(φi,φi)(f,φi)2.