群智优化：探索BP神经网络的最优配置

一、数据集介绍

鸢尾花数据集最初由Edgar Anderson测量得到，而后在著名的统计学家和生物学家R.A Fisher于1936年发表的文章中被引入到统计和机器学习领域数据集特征：
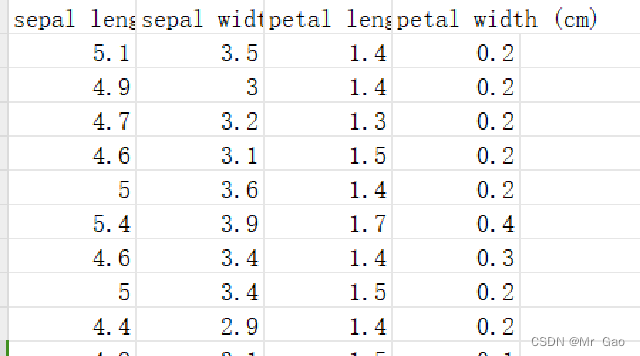
鸢尾花数据集包含了150个样本，每个样本有4个特征，这些特征是从花朵的尺寸测量中得到的，具体包括：
花萼长度（sepal length）：在厘米单位下的花朵萼片的长度。
花萼宽度（sepal width）：花萼片的宽度。
花瓣长度（petal length）：花瓣的长度。
花瓣宽度（petal width）：花瓣的宽度。

二、实验工程

基于粒子群算法的BP神经网络优化

代码如下：

import numpy as np
from pyswarm import pso
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt # 导入matplotlib的库

# 准备鸢尾花数据集
data = load_iris()
X, y = data.data, data.target

# 数据预处理和划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# 定义BP神经网络结构
def create_nn(hidden_layer_sizes, alpha, learning_rate_init):
    return MLPClassifier(hidden_layer_sizes=hidden_layer_sizes, activation='relu',
                         alpha=alpha, learning_rate_init=learning_rate_init, max_iter=1000, random_state=42)


# 定义PSO适应度函数
params_list=[]
accuracy_list=[]
def nn_accuracy(params):
    params_list.append(params)
    hidden_layer_sizes = (int(params[0]),)  # 隐藏层神经元数量，将参数转换为整数
    
    alpha = params[1]  # 正则化参数 alpha
    learning_rate_init = params[2]  # 初始学习率

    # 创建BP神经网络模型
    model = create_nn(hidden_layer_sizes, alpha, learning_rate_init)

    # 使用训练集来训练模型
    model.fit(X_train, y_train)

    # 使用模型对测试集进行预测
    y_pred = model.predict(X_test)

    # 计算模型的分类准确率
    accuracy = accuracy_score(y_test, y_pred)
    accuracy_list.append(accuracy)
    return -accuracy  # 使用负精度作为适应度函数，因为PSO最小化目标函数


# 使用PSO来最大化精度
lb = [1, 0.001, 0.001]  # 参数下界，包括隐藏层神经元数量、正则化参数 alpha、初始学习率
ub = [100, 1.0, 1.0]  # 参数上界

# 使用PSO算法来寻找最佳参数组合，以最大化分类准确率

xopt, fopt = pso(nn_accuracy, lb, ub, swarmsize=10, maxiter=50)

print(xopt, fopt)
# 训练最终的BP神经网络模型，使用PSO找到的最优参数
best_hidden_layer_sizes = (int(xopt[0]),)
best_alpha = xopt[1]
best_learning_rate_init = xopt[2]

best_model = create_nn(best_hidden_layer_sizes, best_alpha, best_learning_rate_init)
best_model.fit(X_train, y_train)



hidden_layer_sizes_list=[]
alpha_list=[]
learning_rate_init_list=[]

for para in params_list:
    hidden_layer_sizes_list.append(int(para[0]))
    alpha_list.append(para[1])
    learning_rate_init_list.append(para[2])
# 评估性能，计算最终模型的分类准确率
y_pred = best_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)



plt.scatter(hidden_layer_sizes_list, accuracy_list, c="red", marker='o', label='hidden_layer_size')#画label 0的散点图

plt.xlabel('hidden_layer_size')# 设置X轴的标签为K-means
plt.ylabel(accuracy)
# plt.legend(loc=2)# 设置图标在左上角
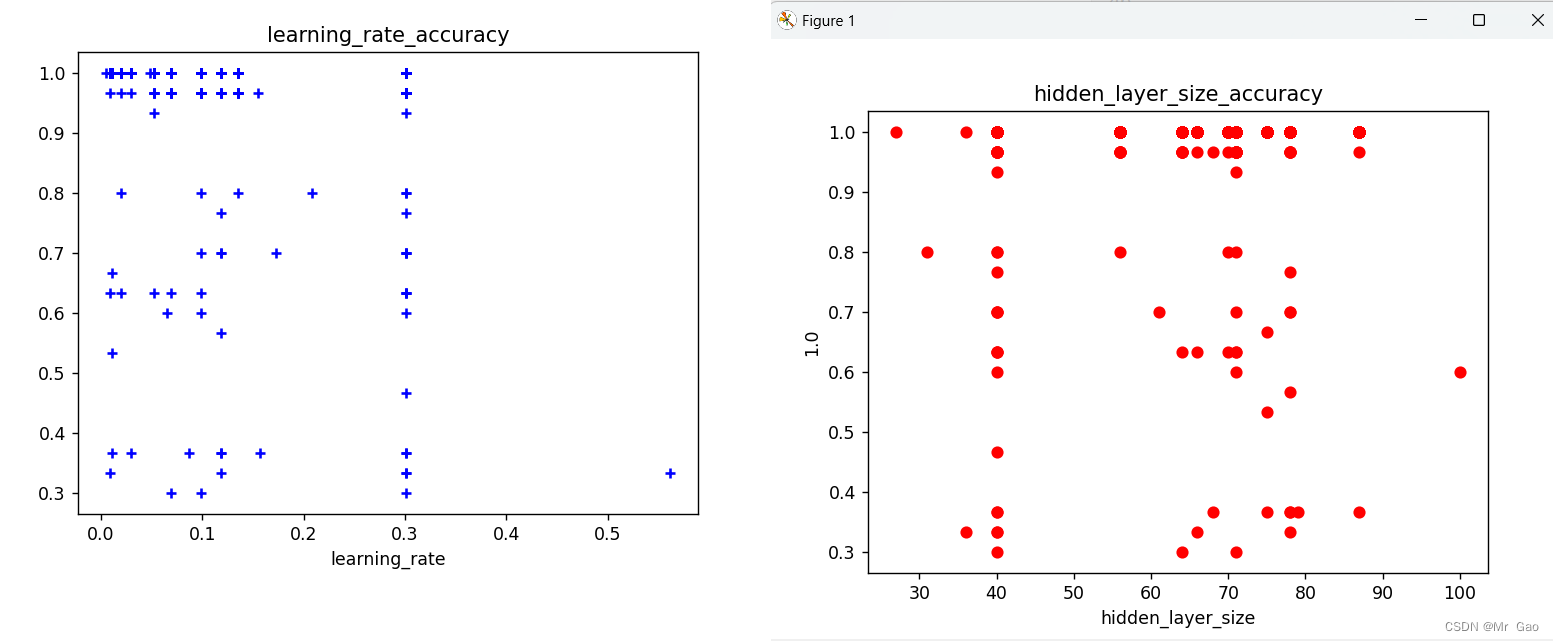
plt.title("hidden_layer_size_accuracy")
plt.show()


plt.scatter(learning_rate_init_list, accuracy_list, c="blue", marker='+', label='learning_rate')#画label 2的散点图
plt.xlabel('learning_rate')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("learning_rate_accuracy")
plt.show()
plt.scatter(alpha_list, accuracy_list, c="green", marker='*', label='alpha')#画label 1的散点图
plt.xlabel('alpha')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("alpha_accuracy")
plt.show()

plt.scatter(range(0,len(accuracy_list)), accuracy_list, c="green", marker='*')#画label 1的散点图
plt.xlabel('iter_num')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("iter_num_accuracy")
plt.show()

print("最终模型的分类准确率:", accuracy)

运行结果：

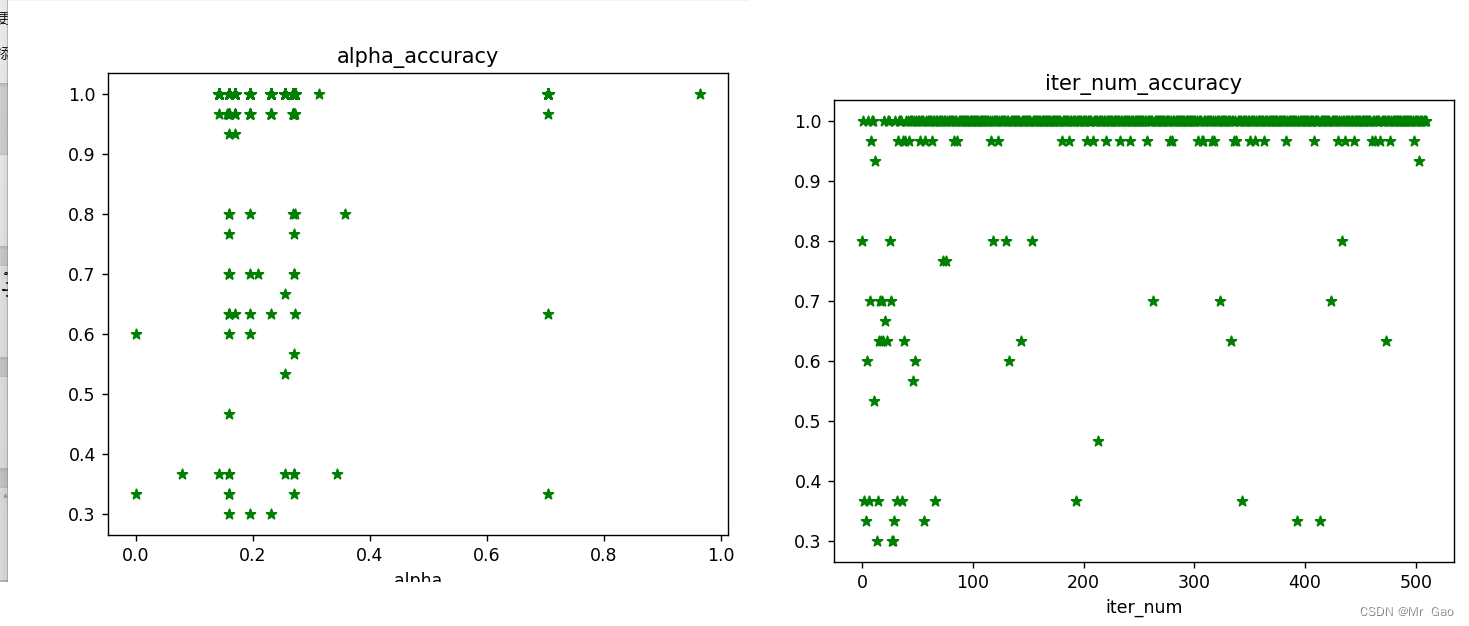
基于遗传算法的BP神经网络优化

代码如下：

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt # 导入matplotlib的库

# 鸢尾花数据集加载
iris = load_iris()
X, y = iris.data, iris.target

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 遗传算法参数
POPULATION_SIZE = 10
GENERATIONS = 50#迭代次数
MUTATION_RATE = 0.1#变异率

# 初始化种群
def initialize_population(pop_size, layer_sizes):
    return [np.random.randint(1, 10, size=layer_sizes) for _ in range(pop_size)]

# 适应度函数
params_list=[]
accuracy_list=[]
def fitness(network_params):
    params_list.append(network_params)
    print('network_params',network_params)
    clf = MLPClassifier(hidden_layer_sizes=network_params[0], activation='relu',
                         alpha=network_params[1]/1000, learning_rate_init=network_params[1]/1000, max_iter=1000, random_state=42)
    clf.fit(X_train, y_train)
    predictions = clf.predict(X_test)
    accuracy_list.append(accuracy_score(y_test, predictions))
    return accuracy_score(y_test, predictions)

# 选择
def selection(population, fitness_scores):
    return [population[i] for i in np.argsort(fitness_scores)[-POPULATION_SIZE:]]

# 交叉
def crossover(parent1, parent2):
    print(parent1)
    child_size = len(parent1)
    print(child_size)
    crossover_point = np.random.randint(1, child_size - 1)
    child1 = np.concatenate((parent1[:crossover_point], parent2[crossover_point:]))
    child2 = np.concatenate((parent2[:crossover_point], parent1[crossover_point:]))
    return child1, child2

# 变异
def mutate(child, mutation_rate, min_value=1, max_value=10):
    for i in range(len(child)):
        if np.random.rand() < mutation_rate:
            child[i] = np.random.randint(min_value, max_value)
    return child

# 遗传算法主函数
def genetic_algorithm(X_train, y_train, X_test, y_test):
    layer_sizes = (3,)  # 
    population = initialize_population(POPULATION_SIZE, layer_sizes)
    print(population)
    for generation in range(GENERATIONS):
        fitness_scores = [fitness(ind) for ind in population]
        selected_population = selection(population, fitness_scores)
        
        new_population = []
        for i in range(0, POPULATION_SIZE, 2):
            parent1, parent2 = selected_population[i], selected_population[i+1]
            child1, child2 = crossover(parent1, parent2)
            child1 = mutate(child1, MUTATION_RATE)
            child2 = mutate(child2, MUTATION_RATE)
            new_population.extend([child1, child2])
        
        population = new_population
        
        # 打印当前最佳适应度
        best_fitness = max(fitness_scores)
        print(f"Generation {generation}: Best Fitness = {best_fitness}")
    
    # 返回最佳个体
    best_individual = population[np.argmax(fitness_scores)]
    return best_individual

# 运行遗传算法
best_params = genetic_algorithm(X_train, y_train, X_test, y_test)

# 使用最佳参数训练BP神经网络
clf = MLPClassifier(hidden_layer_sizes=tuple(best_params), max_iter=100, random_state=42)
clf.fit(X_train, y_train)



hidden_layer_sizes_list=[]
alpha_list=[]
learning_rate_init_list=[]

for para in params_list:
    hidden_layer_sizes_list.append(int(para[0]))
    alpha_list.append(para[1])
    learning_rate_init_list.append(para[2])



#



plt.scatter(hidden_layer_sizes_list, accuracy_list, c="red", marker='o', label='hidden_layer_size')#画label 0的散点图

plt.xlabel('hidden_layer_size')# 设置X轴的标签为K-means
plt.ylabel('accuracy')
# plt.legend(loc=2)# 设置图标在左上角
plt.title("hidden_layer_size_accuracy")
plt.show()


plt.scatter(learning_rate_init_list, accuracy_list, c="blue", marker='+', label='learning_rate')#画label 2的散点图
plt.xlabel('learning_rate')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("learning_rate_accuracy")
plt.ylabel('accuracy')
plt.show()
plt.scatter(alpha_list, accuracy_list, c="green", marker='*', label='alpha')#画label 1的散点图
plt.xlabel('alpha')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("alpha_accuracy")
plt.ylabel('accuracy')
plt.show()

plt.scatter(range(0,len(accuracy_list)), accuracy_list, c="green", marker='*')#画label 1的散点图
plt.xlabel('iter_num')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("iter_num_accuracy")
plt.ylabel('accuracy')
plt.show()

# 测试神经网络
predictions = clf.predict(X_test)
accuracy = accuracy_score(y_test, predictions)
print(f"Test Accuracy: {accuracy}")

运行结果：

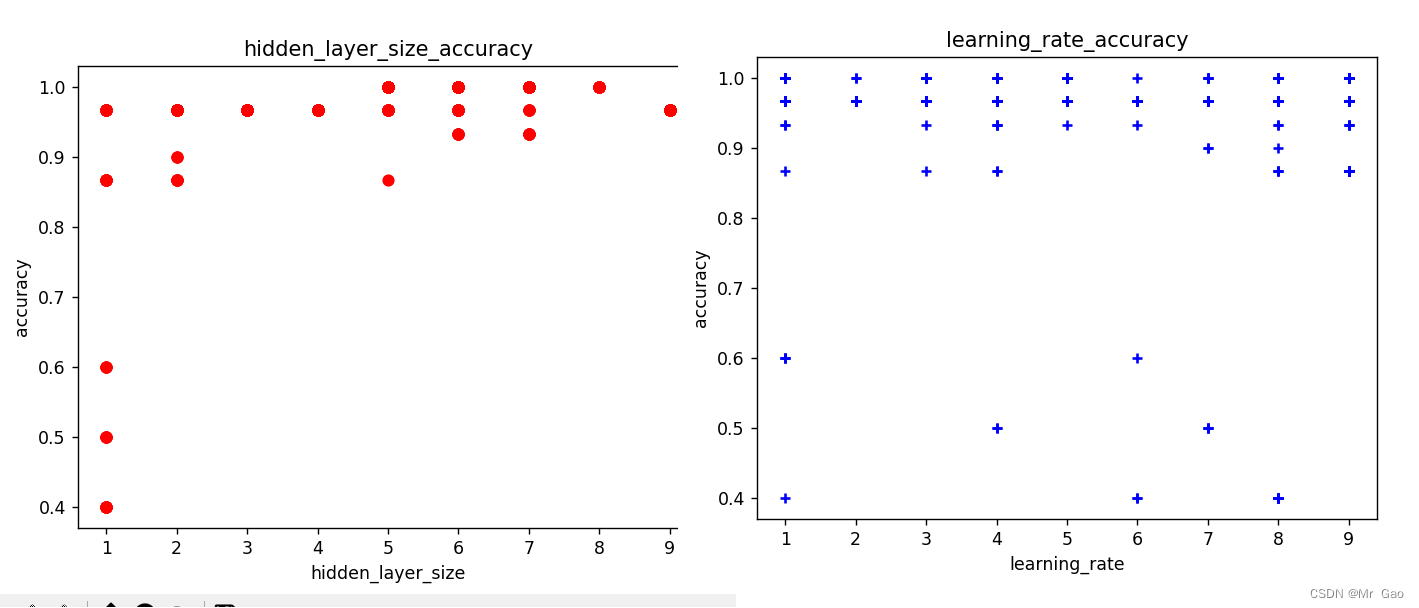
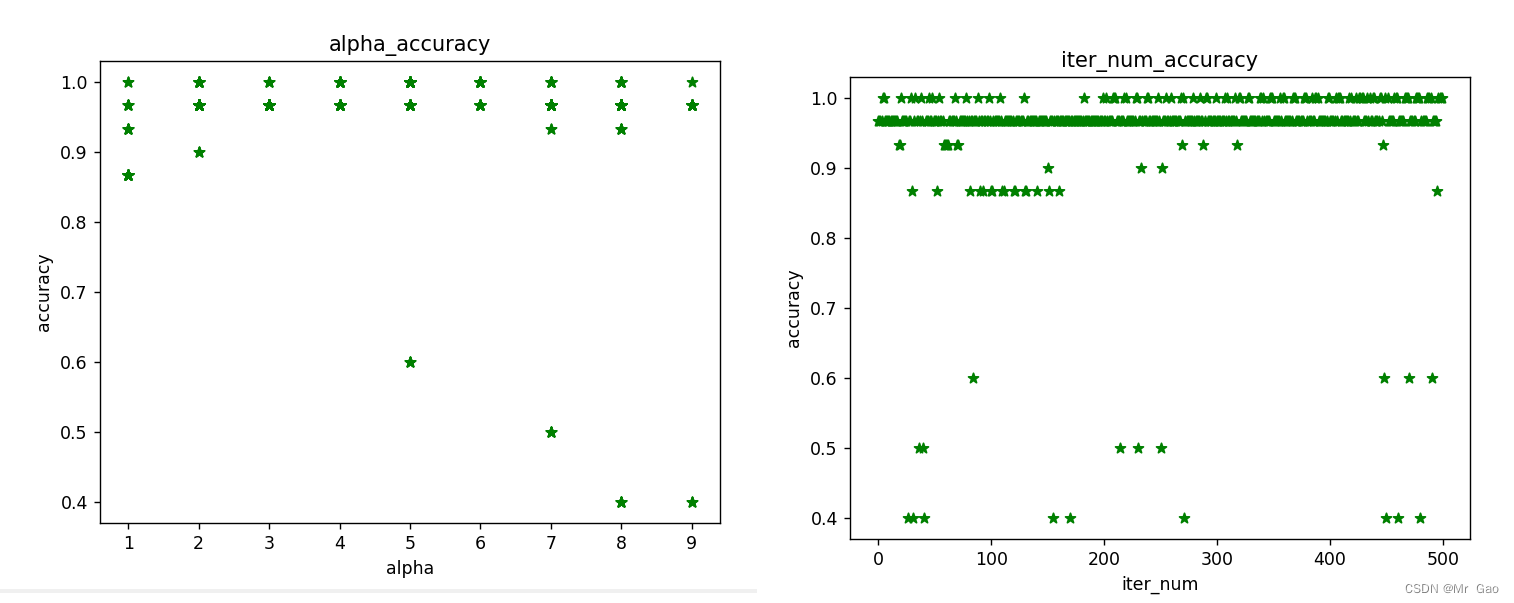
总结

1.优化效果显著：实验结果表明，通过粒子群优化和遗传算法相结合的方法对BP神经网络的隐藏层数量、神经元数量以及其他超参数进行调整后，网络在多个标准数据集上的表现得到了显著提升。

2.算法优势互补：粒子群优化在全局搜索能力上表现突出，而遗传算法在局部搜索上更为精细。两者的结合充分利用了各自的优势，提高了算法的搜索效率和精度。

3.适应度函数的重要性：在本研究中，适应度函数的设计对于算法的性能至关重要。通过精心设计的适应度函数，可以更有效地引导算法搜索到最优解。

4.计算成本与性能的平衡：虽然结合算法提高了优化精度，但同时也增加了计算成本。未来的工作需要在计算效率和优化精度之间找到更好的平衡点。