目录

一、 Recast生成

(一) 概述

1． 简介

(二) 生成过程

1． 体素化

2． 区域

3． 轮廓

4． 生成凸多边形

5． 详细三角形

(三) 配置

1． 可配置参数

2． 数据结构

(四) 项目应用

1． CS体系方案

2． 资源管理

3． 业务逻辑应用

二、 Detour算法

(一) 概述

1． 简介

2． 服务器选型

(二) 定位多边形

1． 概述

2． 包围盒

3． 定位Tile

4． 有效多边形

5． 点在多边形内

6． 求解高度

(三) 射线探测

1． 概述

2． 算法详解

3． 问题与优化

4． 参考分析

(四) 寻路

1． 概述

2． A星选型

3． 优化思考

(五) 路径平滑

1． 概述

2． 算法思路

3． 漏斗详解

4． 算法思考

(六) 详细路径

1． 问题分析

2． 公共边交点

3． 应用流程

Recast生成

概述

简介

基础流程

将代表原始场景的obj模型文件，生成可以描述场景详细信息的点bin文件的过程。

烘焙方式

根据最后数据的管理结构不同，区分为三种类型的烘焙方式。

Tile-Mesh：将整张地图划分为多个tile，以tile作为管理的最小单位。

Solo-Mesh：以整张地图为管理单位，理解为一个大tile。

Obstacles：管理方式同Tile-Mesh。但是其保留了体素数据，支持动态阻挡。

坐标系选择

常规坐标系分为，“左手坐标系”和“右手坐标系”。左右手坐标系之间互为“镜像”关系。Recast采用的是“右手坐标系”。

镜像关系：坐标原点相同，如果任意两轴相同，则第三轴互为相反关系。

左手坐标系：XYZ轴对应左手的拇指，食指，中指。三指互相垂直即可。

右手坐标系：XYZ轴对应右手的拇指，食指，中指。三指互相垂直即可。

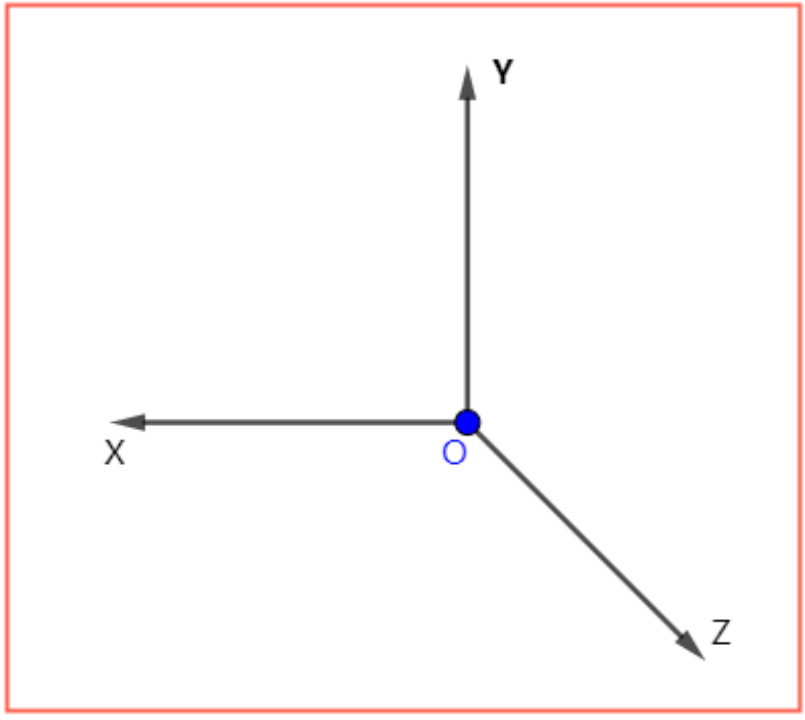
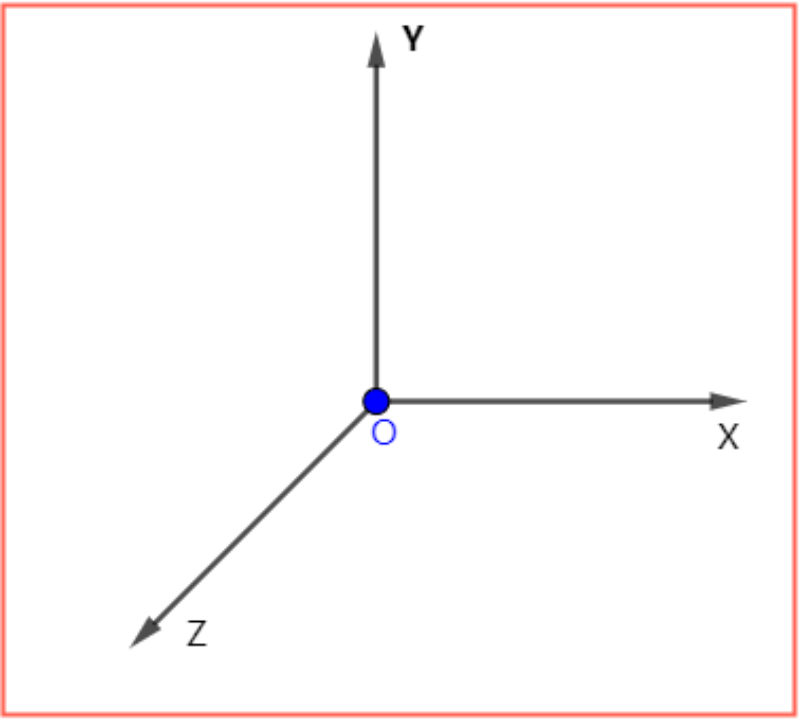
观察上述两图，两类坐标系互为：关于同Y-Z双轴平面下的“镜像”关系。

生成过程

体素化

概念

理解体素，可以直接对照像素的概念，二者的区别就是把维度从二维提升到三维。

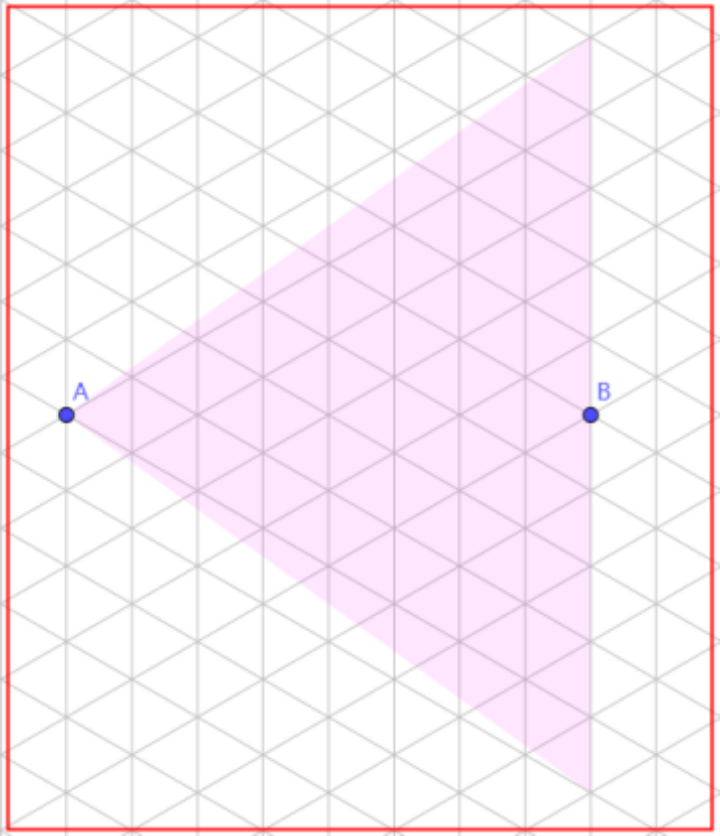
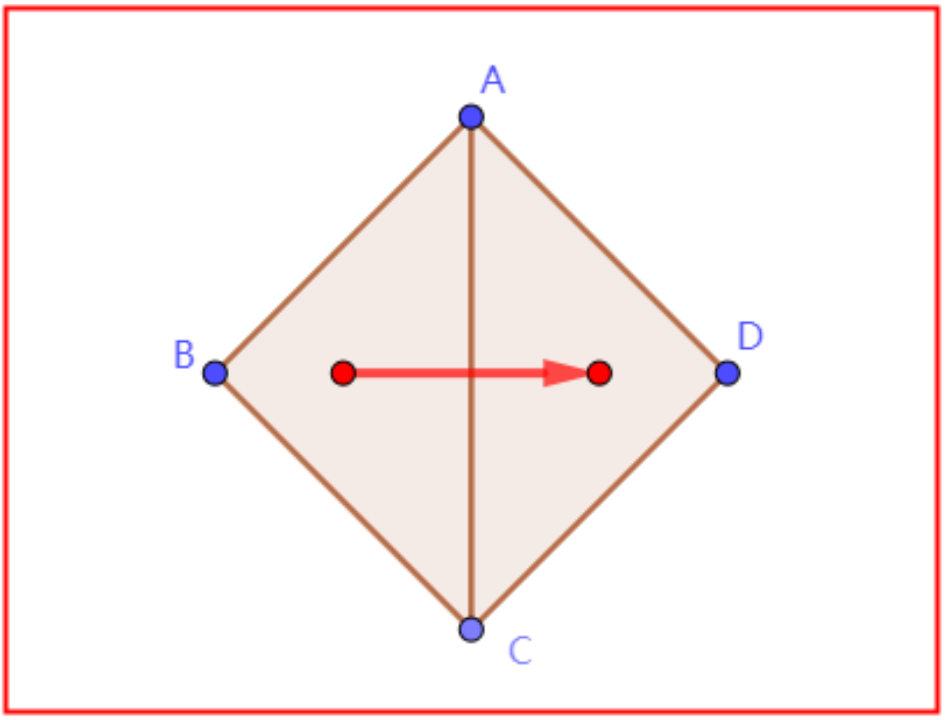
像素：由若干等大方格来描述一个二维平面图。如图，四边形ABCD就可以用该多边形所包含的所有方格的集合来描述。

体素：由若干等大方体来描述一个三维立体物。

需要注意的是，无论是像素还是体素，都是采用的“极限拆分”思想，本质上都是用更小粒度的拆分单元来组合成一个更大粒度的组合集合。这种方法必然存在误差，而拆分单元的粒度决定了误差的大小。

体素化（Voxelization）：表示再形成过程。将基于边界的表现形式（例如：多边形模型，曲面等）转换成为体积的表现形式（例如：体素块）。

体素块

体素块就是上述的“拆分单元”，即用于表示物体空间的最小组成元素。

对整个场景创建一个最小将其包含的“包围盒”。

将“包围盒”进行横、竖、纵向等大切分，形成拆分单元（体素块）。

上述创建的一个包含体素块信息的管理体系，称为“高度场”。

高度场

计算高度区间

所谓的计算高度区间，就是在高度场中，求解出每一个空间实体所相交的体素块的集合。该集合即为描述对应空间实体的体素化数据。这些集合中的体素块，有连续的，也有不连续的。。

当计算完相交信息后，一个体素块根据是否有与之相交的实体，相应的产生两种状态：代表实体物的实心体素块，以及没有实体物的开放体素块。

每一个实心体素块还有一个关键信息，就是其与实体空间相交面。该相交面会与水平面X_Z平面形成一个夹角A。根据夹角A与配置参数“最大可爬坡夹角B”的比较，为实心体素块创建一个标识信息。

判断A与B：

当A大于B的时候，将当前体素块的标识信息置为“不可走”。

当A小于B的时候，将当前体素块的标识信息置为“可走”。

一般来说，我们只关心高度场的实体区域，此时把每一列上连续的实心体素块的整体，称为“高度区间（Span）”。而每一个高度区间最上面的一个体素块的标志位就是当前高度区间“是否可走”的标识。

合并高度区间

每当产生一个新的高度区间new_span，其就有可能与已产生的高度区间old_span在空间上产生冲突，也就是高度区间的交集。一旦产生了交集，就意味着这两块独立高度区间在高度场中是连续的。而高度区间的“合并”，就是将两个有交集的高度区间合并成两者的并集。

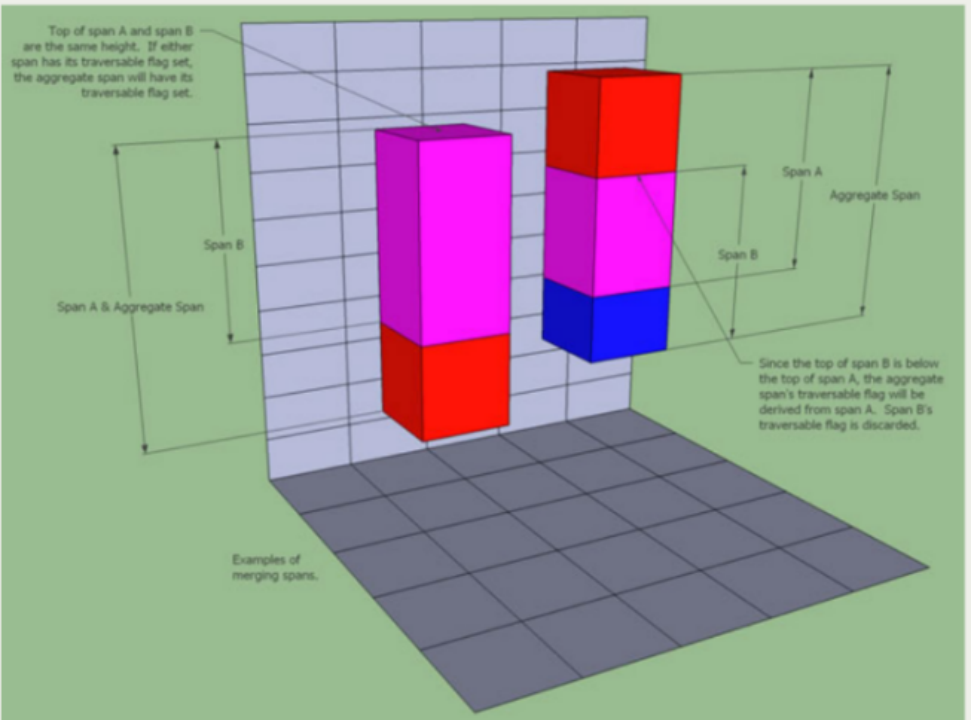
怎么根据合并前的高度区间决定合并后的“是否可走”标志呢？

新旧span的高度不同时，合并标志置为高span的标志。

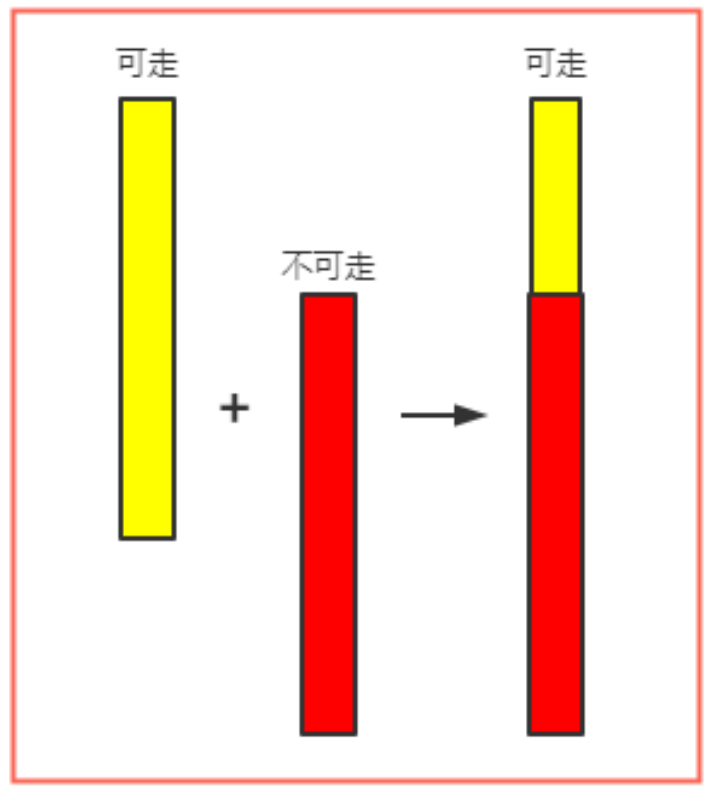
新旧span的高度相同时，二者任意一个可走，合并标志即可走。

分析下图，为什么水平线和斜线交接的地方是“可走”的。其实这个交接位置就是两个体素块合并后的结果。在计算水平线的体素块的时候，交界处是“可走”的，在计算斜线的体素块的时候，交接处是“不可走”的。但是二者重叠合并，通过合并规则设置其为“可走”的。

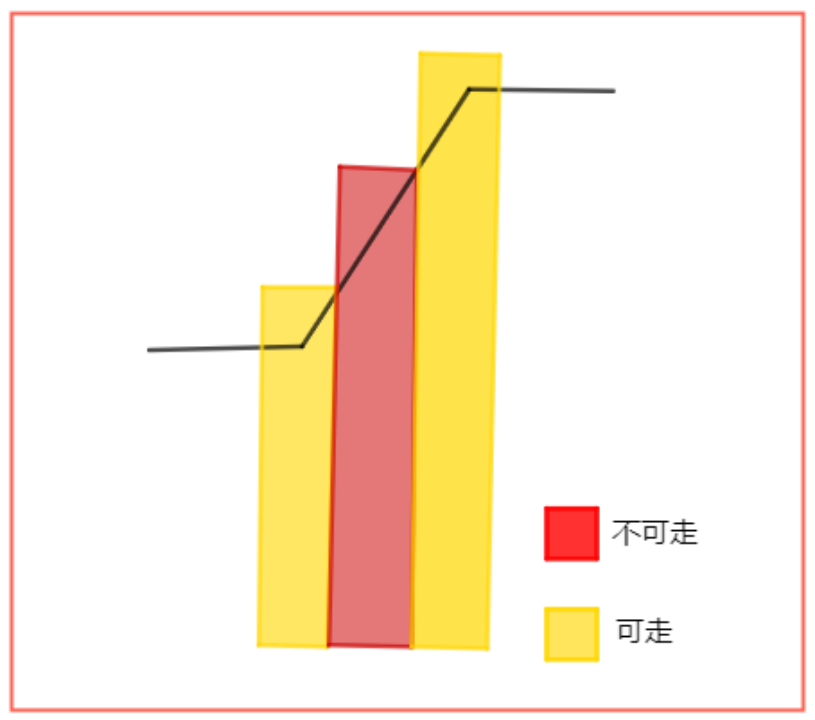
过滤高度区间

高度区间代表实体体素（受阻空间）的跨度。高度区间会有一个标志信息，该信息说明当前跨度的顶面是否是“可行走”的。但是到目前为止，该标志仅仅取决于原obj文件中多边形的斜率。所以，需要根据一些配置参数和逻辑关系来进行该标志位的过滤。

支持三种过滤方式，各方式之间相互独立，且都非必须执行（可选项）。但是，Low_Hanging_Obstacles的效果会覆盖Ledge_Spans，所以如果上述两个选项被同时选择，则后者必须在前者之后执行。

Low_Hanging_Obstacles：不可走变可走

为了在低洼区域形成可走区域。比如，路边，楼梯等，将不可走标记为可走。

具体实现：

迭代每一列，从下往上遍历span，对于同列任意两个相邻的span1（下）和span2（上），当span1可走，并且span2不可走的时候，计算这两个span的上表面高度差Diff，如果Diff小于配置参数“可爬坡高度”，则将span2设置为“可走”。

Walk_Low_Height_Spans：可走变不可走

同列相邻两区间之间距离的校验，保证最小可通过距离。

具体实现：

迭代每一列，从下往上遍历span，如果当前span不可走，直接跳过。

否则，计算当前span_B的上表面和其上相邻的span_A的下表面之间的高度差Diff。span_A不存在的话，高度差Diff设为无穷大。

如果“高度差Diff”小于“配置可走高度”，则将当前span的标识位置为“不可走”。

Ledge_Spans：可走变不可走

峭壁区间检查，这种过滤器会首先查找当前span的所有“有效邻居区间”。需要注意的是：如果当前span已经不可走，则直接跳过了。

具体实现：

当前迭代区间为span1，遍历四个方向的轴邻居列，从下往上迭代轴邻居列的高度区间span2。

假设span1的上面还与其有同列相邻的span4，span2上面有与其同列相邻的span3。如果span3或span4不存在，则认为其高度为无穷大。

计算max(span1, span2)和min(span3, span4)的差值Diff，如果Diff大于“配置可走高度”，则认为span2是一个“有效邻居区间”。可以证明，每一个轴邻居列上最多只会存在一个“有效邻居区间”。

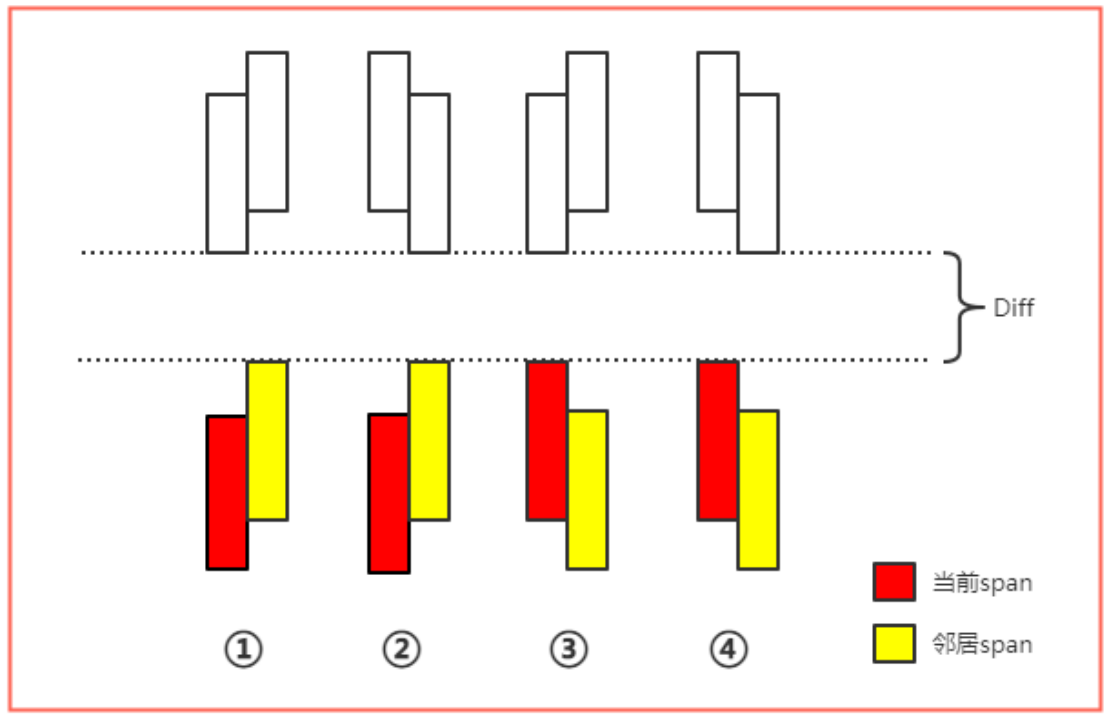
可以很明显的看出，“有效邻居区间”限定了两种情况。如图所示，当Diff大于“配置可走高度”的时候，①②说明“可爬坡”且“不碰头”，③④说明“可下坡”且“不碰头”。

找到所有“有效邻居区间”后，过滤器会继续过滤“峭壁区间”。

具体实现：

如果有任意轴邻居列上没有任何“高度区间”，则认为当前span是”峭壁区间“。

如果有任意轴邻居列上没有”有效邻居区间“，则认为当前span是“峭壁区间”。

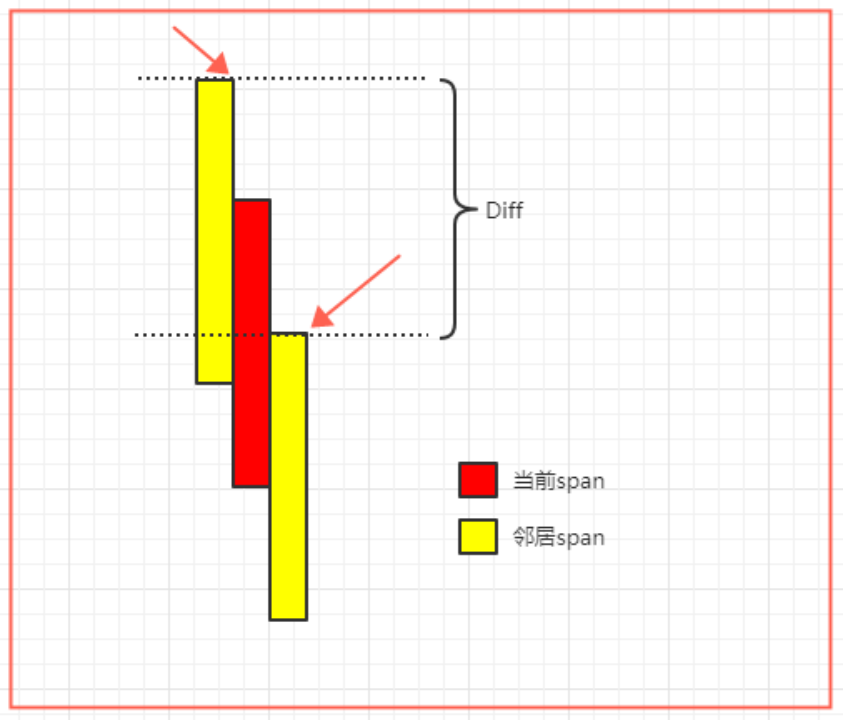
如果有任意轴邻居列上存在“有效邻居区间”span2，span2的上表面低于span的上表面，且span和span2的上表面高度差Diff大于配置参数“可爬坡高度”，则认为当前span是”峭壁区间”。

如果当前span本来可走，且判断为“峭壁区间”，则设置为“不可走”。

在不满足峭壁区间的情况下，才会继续判断“间接峭壁区间”。

过滤间接峭壁区间，具体实现：

前提：在当前span的四个轴邻居上的“有效邻居区间”中。

所有上表面高于span上表面的“有效邻居区间”中，上表面最高的“有效邻居区间”的上表面高度设为a。

所有上表面低于span上表面的“有效邻居区间”中，上表面最低的“有效邻居区间”的上表面高度设为b。

如果a减b大于配置参数“爬坡高度”，则认为当前span处于峭壁上--间接峭壁区间。

如果当前span本来可走，且判断为“间接峭壁区间”，则置为“不可走”。

邻居

当高度场中的体素块是方体的时候，我们认为每一个方体的邻居就是其周围一圈的其他方体，即“九宫格”中以自己为中心的其他八个位置的方体。

根据其相对位置的不同，邻居又分为轴邻居和对角邻居。后续所有的操作几乎只关心轴邻居，原因很简单，对角邻居就是轴邻居的轴邻居。

轴邻居：前后左右偏移的邻居

对角邻居：对角偏移的邻居

剔除边缘

到目前为止，已经根据配置参数“爬坡角度”、“可走高度”、“爬坡高度”进行了一些逻辑上的过滤。此时考虑游戏可移动物Agent在场景边界移动的情况，如果距离边界过近，会出现Agent的一部分在边界之外，如果边界是墙体等可视化阻挡的话，会较低游戏的视觉体验。所以提供配置参数“Agent半径”，然后根据该半径进行“边缘剔除”。

此时的做法是对每一个“可走高度区间”加上一个“逻辑距离”的概念。该距离在逻辑上标识当前高度区间距离某个最近边界的距离，然后以该逻辑距离与配置参数比较，从而将那些距离边界过近的边缘区域剔除。

具体实现：（以每一层的二维矩阵为例，所有区间初始逻辑距离均为逻辑无穷大，设为dist()=max）

特殊情况：所有不可走区间，逻辑距离为0。所有“有效邻居数量”不为4的区间，逻辑距离为0。

先从左下角向右上角遍历，由正左方轴邻居开始，逆时针遍历四个邻居。原因很简单，其他邻居位置还没有被遍历到，也就是在算法执行过程中，还是无效的。

遇到轴邻居，当Dist(轴邻居)+2<dist(自己)的时候，将自己的逻辑距离更新为Dist(轴邻居)+2。

遇到对角邻居，当Dist(对角邻居)+3<dist(自己)的时候，将自己的逻辑距离更新为Dist(对角邻居)+3。

当上述一次遍历完成后，再逆向遍历即可，此时的计算将以正右方轴邻居开始，逆时针遍历四个邻居。由此，完成对每一个高度区间的所有八个邻居的相对关系的计算。

当计算出所有高度区间的逻辑距离后，对比每一个高度区间的逻辑距离diff和配置参数“可走半径”的2倍，也就是可走直径作对比，所有不满足可走直径的高度区间，全置为“不可走”。

（上述计算过程中的2,3这些自然数全是逻辑数值，代表的是几个单元格边长。算法执行之前，也会将参与运算的配置参数，转换成以单元格边长为单位的逻辑数值）

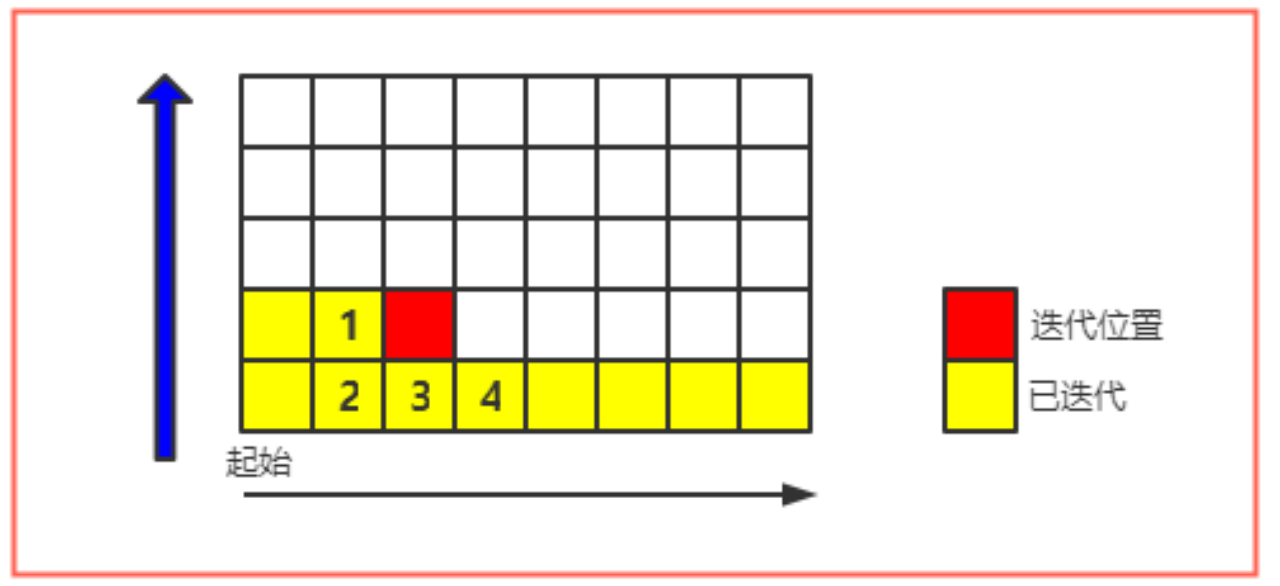
实体区间和开放区间

通过上述阐述，计算完高度区间后的高度场可以分为两种类型。

实心高度场：所有实体高度区间的集合

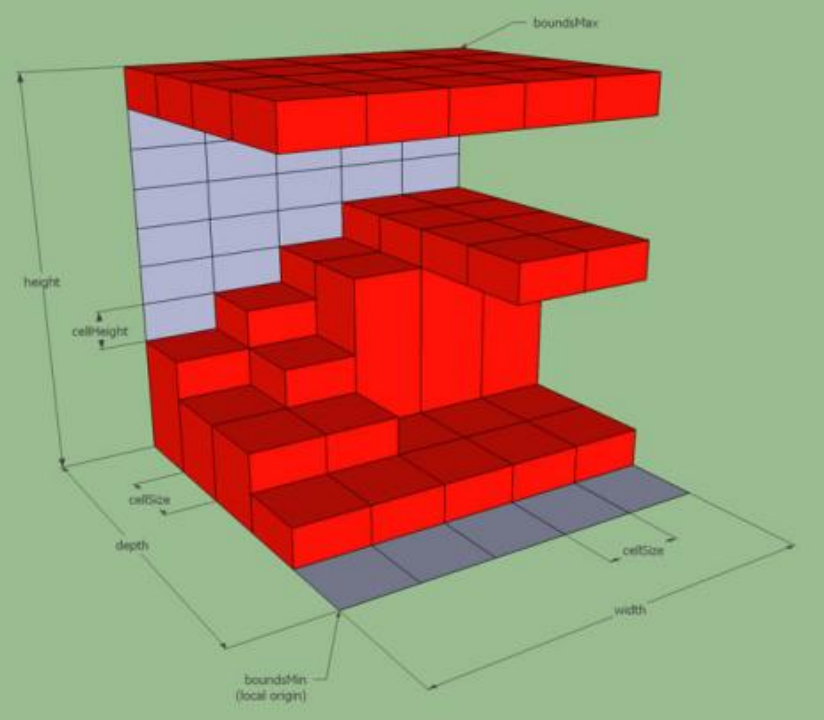
开放高度场：所有实体高度区间的上方非实体空间

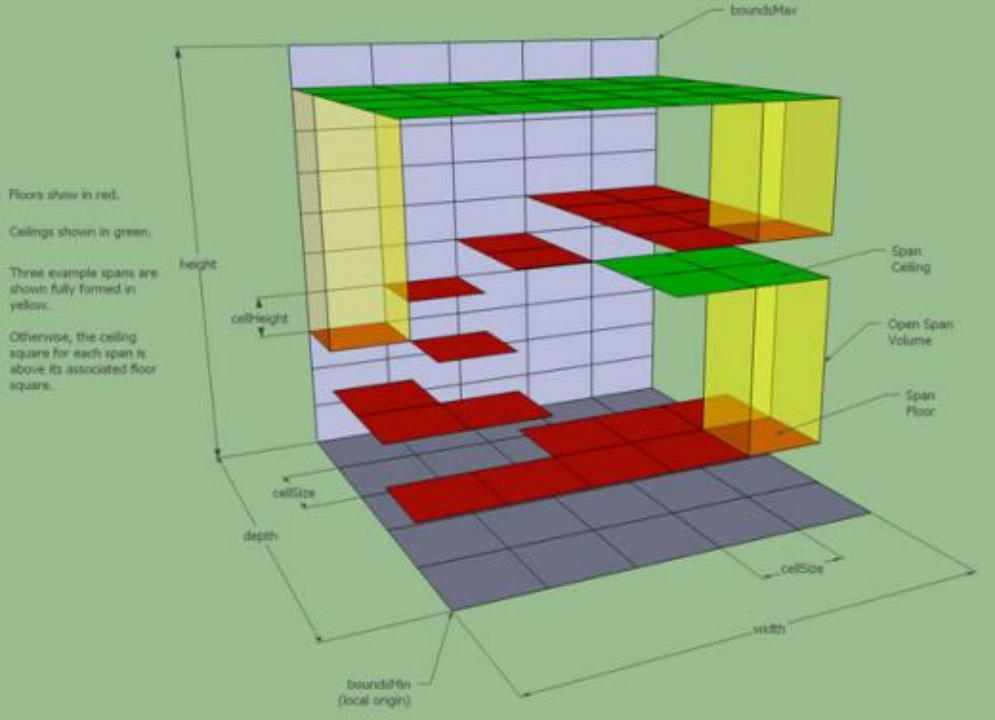
需要注意的是，两种类型并非互补关系。如果当前列中没有任何实体高度区间，则当前列空间不属于任何一种高度场。并且一列中最底下一个实体高度区间的下方也不属于任何一种高度场。

我们关心的其实是开放高度场，也就是实心高度场的上表面和下表面。这与数据结构无关，无论结构如何组织，其逻辑都可以相互转换。

区域

概述

体素化让我们得到了所有描述实物的场景信息，现在是时候将他们关联起来了（体素化过程中也有一步合并区间，但那仅仅是为了解决空间冲突）。

区域（Region）针对的是局部有内在联系的多个相邻列的整体。将独立的列信息之间利用一些规则进行整合，从而实现将整个场景划分成一片一片的区域。

区域生成

三种不同的方式，以及各自的优缺点。

Watershed：分水岭算法，最传统的生成区域的方式，生成效果最好，后续算法不会产生细长多边形。但是由于其算法的复杂性，在性能上是最慢的，一般用于离线处理，适合大地图。

Monotone：单调算法，注重效率，在性能上是最快的。但是，缺点很明显，会导致后续的处理出现大量的细长多边形，效果不好。

Layer：分层算法，折中思想，效果与性能都处于上述两种算法之间，目前选择的使用方式。

区域过滤

由于区域生成算法是依赖于上层场景的，由于游戏场景的无限制性，无论我们如何控制区域生成算法，都必然由于原场景的特异性导致一些奇怪的或者我们不希望出现的区域。例如，石子路面上有大量的石子，有的石子很大，但是其相对于路来说，不值一提，我们不希望这些石子形成自己的区域。

此时就需要“过滤”某些区域，以此来增强对区域生成的控制。

未连接的最小区域：没有连接到任何其他的区域，且自身区域大小小于当前配置参数的区域，将被剔除。

合并的最小区域：区域大小小于这个配置参数的区域，将在任何有条件的情况下，与其他较大的区域进行合并。

过滤区域算法的目的就是帮助减少不必要的小区域的数量，这一步会很大程度的减少后续处理的复杂度。

轮廓

概述

在经过区域生成之后，我们得到了单独高度区间经过处理后的局部逻辑整体。如何区分和管理这些整体，对之后的处理显的尤为迫切。此时区域与区域之间的分界就是非常重要的信息了。而轮廓（Contour）就是描述区域边界的概念。

约定两种边的概念：内部边，边界边。

内部边：区域内部邻居之间的边。例，2和4。

边界边：区域与其他不属于该区域位置的交界。例，1和2，2和3。

轮廓查找算法

我们将寻找一块有效区域的所有边界边的方法，称为“轮廓查找”。

方法概述（以生成顺时针轮廓为例）：

找到区域任意一个边界边A，以当前边界边开始算法。

如果当前是边界边，将当前边界边添加到轮廓中，然后顺时针旋转90度，继续判断旋转后的边。

如果当前是内部边，则进入到共当前边的邻居内，然后逆时针旋转90度，继续判断旋转后的边。

直到回到边界边A为止，结束，此时依次添加进轮廓中的所有边界边全部查找完毕。

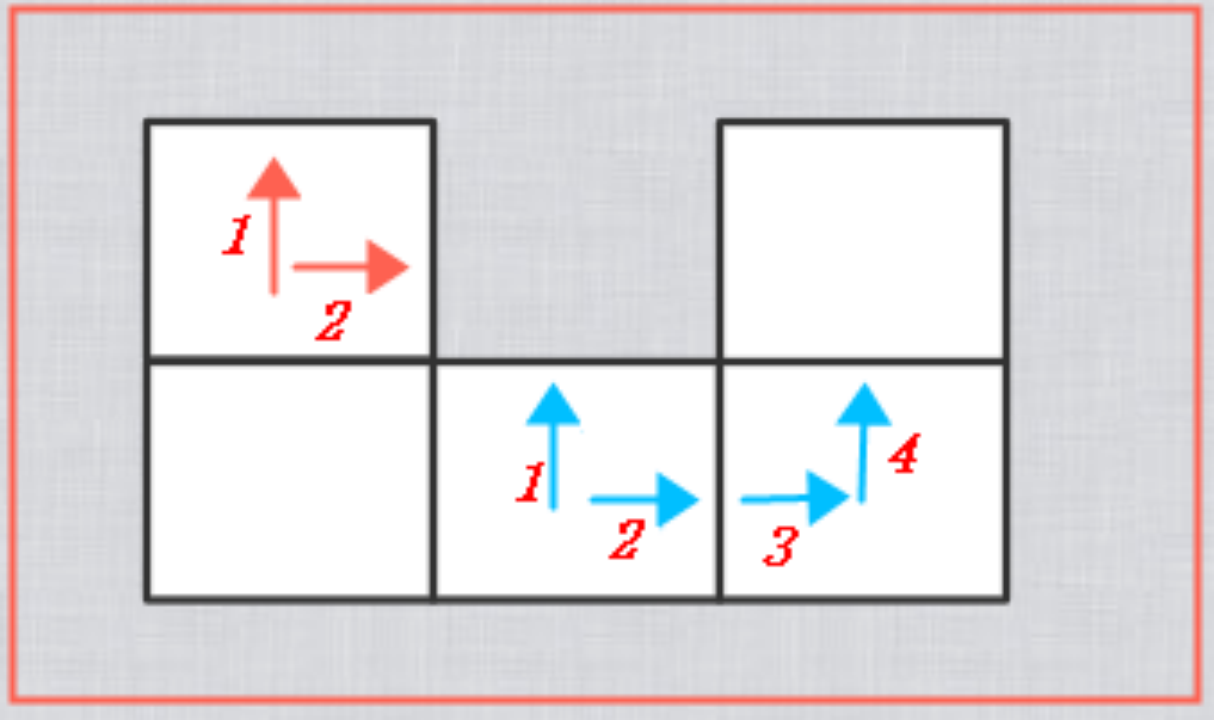
简化轮廓

考虑这样一个问题，我们的体素块的大小粒度对于可视化场景来说，是非常小的（粒度太大，体素化的效果太差）。这就在生成轮廓后导致，很多边界都呈现出一种左右摇摆的锯齿形状。这无形中增加了很多维护信息以及复杂程度，因为我们不希望一条长线段能解决的问题，非得去处理五条短线段的集合。我们希望区域的轮廓是右图尽量规整的情况，而不是左图的锯齿状。

轮廓细分

约定两种轮廓的概念：连接轮廓，边界轮廓。本约定是对“边界边”又进行了更小粒度的划分。

连接轮廓：连接两个有效区域之间的边界边。

边界轮廓：有效区域与空区域之间的相交的边界边。

强制性顶点

约定一种顶点的概念：强制性顶点

强制性顶点：区域连接发生变化的顶点，连接轮廓与边界轮廓相交的顶点。

考虑一种特殊情况，可以很容易证明出，并不是所有的区域都有“强制性顶点”，此时如何进行上述算法呢？很简单，随便找两个相对较远的顶点作为强制性顶点即可。Recast的做法是，连接轮廓与边界轮廓相交的顶点。

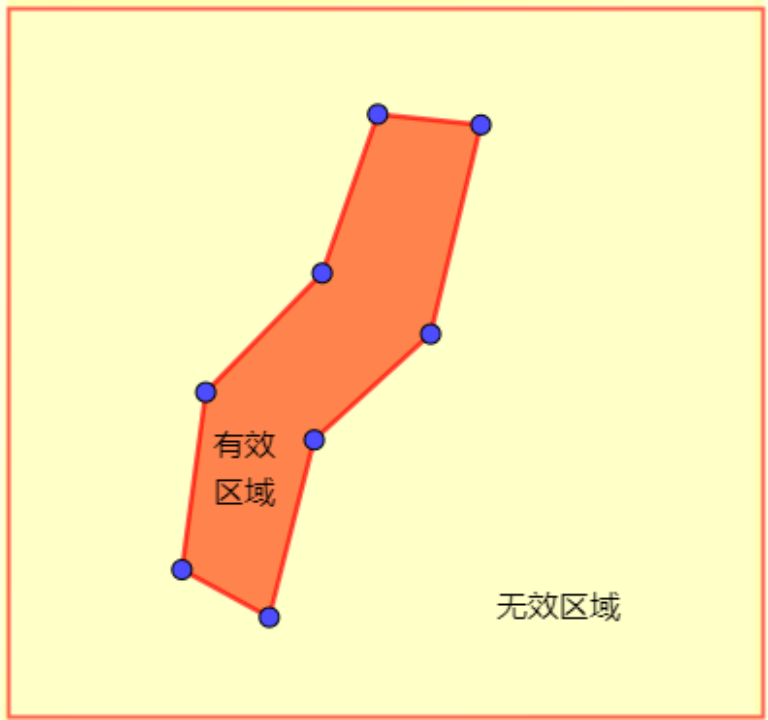
优化轮廓

针对不同的轮廓边进行一定程度的优化。

优化连接轮廓：只留下“强制性顶点”，废弃其他顶点。

方法概述：

对于连接两个有效区域的连接轮廓，找到其两个“强制性顶点”，直接连线，忽略中间的所有“非强制性顶点”。

思路分析：

其实这种思路建立在一个非常有趣的前提下，即在两个有效区域交界的地方，不必过于在意该位置到底该归属于哪一个有效区域。考虑这样一种情况，大海的边界是沙滩，沙滩的边界又是大海，其实在两者交界的那部分区域，属于大海还是属于沙滩的意义根本不大。

那为什么边界轮廓不能用这种方法呢？上述思路成立的前提是两个有效区域，而有效区域和空区域之间，就有必要进行区分了，至少不能让误差过大。

优化边界轮廓：控制“左右摇摆”的幅度，实现允许误差内的“平滑”。

方法概述：

找到“边界轮廓”的两个端点S和E，连接SE做连线L，称为“基准线”。此时不是直接丢弃其他点，而是做“平滑”处理。在其内的其他顶点中找到距离Dist（点到直线距离）基准线最远的点A，判断该距离Dist与参数“允许最大边界误差”的大小关系（是否在误差允许范围内）。

如果点A大于允许误差范围，则认为点A是相对于该基准线的“无效点”。此时，处理无效点，用其相对的基准线的两个端点分别与之相连做出新的基准线，然后重复上述过程。

直到所有点到与其相对的基准线的距离都在允许误差内，结束优化。

思路分析：

思路来源很简单，数学上常用的“曲线平滑算法”的变种。

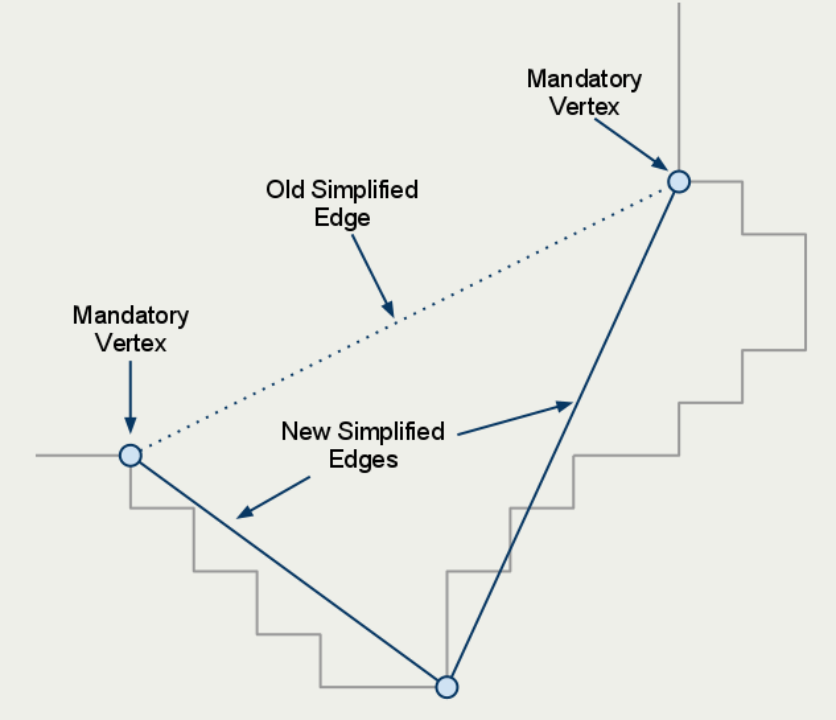
轮廓限制

考虑一种正常情况，优化轮廓的初衷，是为了使用更少的点来描述轮廓的边界，试图使得轮廓更加“规整简单”。但是，越减少轮廓边界的点，就意味着两点之间的轮廓线段越长。这种情况的产生具有“必然性”，其直接导致了后续“轮廓划分三角形”的时候出现“狭长三角形”，从而间接影响了寻路算法。

此时的常规做法是，在简化轮廓的同时，限制其简化的程度，在两者之间取得一种平衡，配置参数“最大轮廓边长”限制了允许的最大两点之间的距离。

方法概述：

在进行轮廓优化的时候，出现了超过“限制最大轮廓边长”的时候，会用“二分法”不断添加中点，形成新的短边。直到所有边的长度都满足限制。

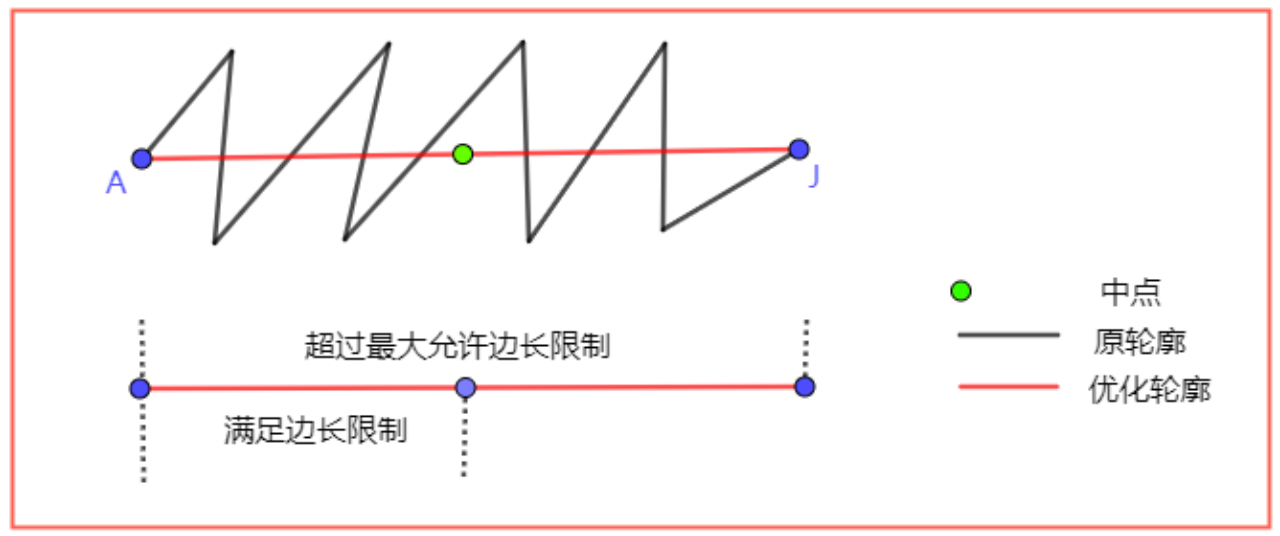
生成凸多边形

概述

有了轮廓的数据之后，就有了一片区域的边，那么此时就需要对区域进行更加详细的定位，例如寻路是要具体寻到某一个点，并且区域内部任意两点并不是一定直线联通的，所以要将区域划分成更加细化的可以描述整个区域面的信息的数据。此时采用的是将区域划分成一些凸多边形的集合，这些凸多边形的并集就是整个区域。

为什么必须使用凸多边形呢？是因为凸多边形在几何上就限定了其形状的规范性，至少其能保证，其内部任意两点之间是直线联通的，这对于后续算法有很重要的意义。

三角划分

有很多经典的“三角剖分”算法，比如比较经典的“翻边算法”、“逐点插入算法”、“分割合并算法”——这些都是基于离散点的Delaunay三角剖分算法。而现在的需求其实是对多边形进行三角划分，此处只讨论使用的针对“凹多边形”的三角划分算法（凸多边形同样适用，并且更简单）。

针对凹多边形的三角划分，算法概述：

每次迭代凹多边形，将其分成两部分，一个三角形和剩余的部分。然后迭代“剩余的部分”，继续划分，直到没有三角形可以划分位置。

算法的核心点是如何对每次的“剩余多边形”划分出一个三角形。

采用的方法很简单，基于“任意不共线三点构成三角形”的理论，每次寻找多边形相邻的两条边，如果其不共直线，那么连接这两条边的三个端点，就可以形成一个三角形。

但是需要注意的是，这样形成的三角形可能会是多边形外部的，注意区分剔除即可。

构建“分割边”

以任意端点开始，沿着一个方向依次去找两个边，如果两个边不共线，则连接两边不重合的点，形成一条连线，称为“分割边”。对每一个点进行该过程，会形成很多分割边，剔除那些在多边形外部的分割边，剩余的就是有效分割边。

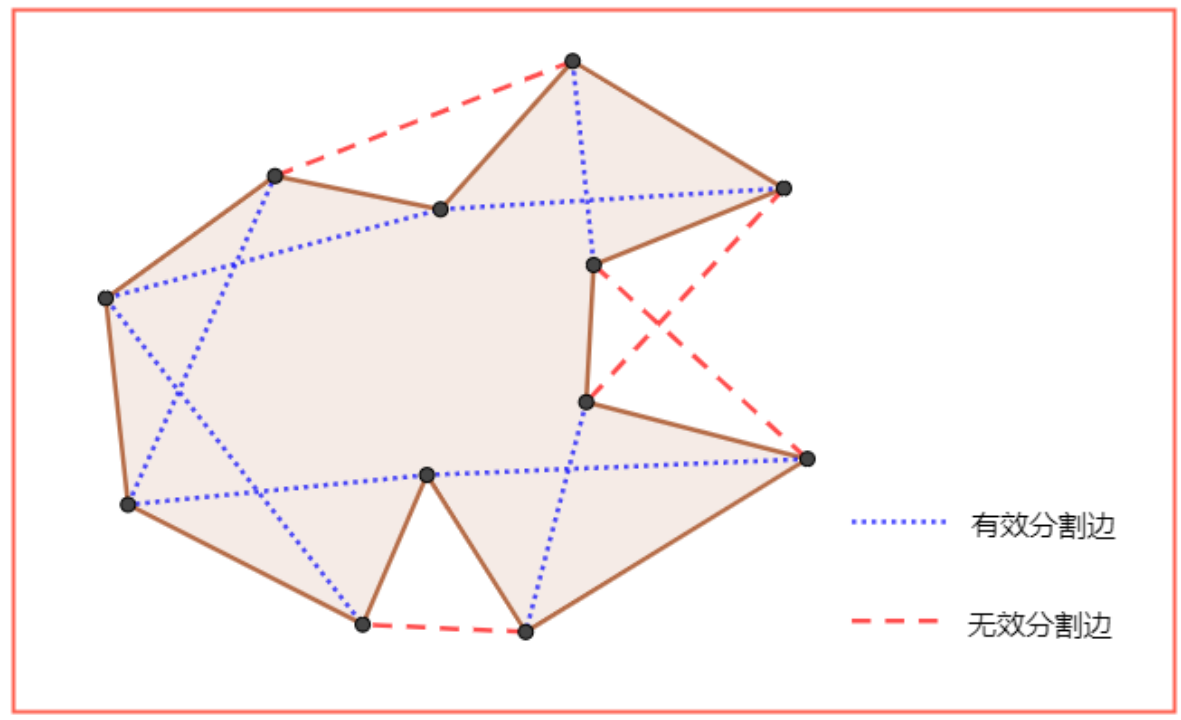
划分三角形

在上述所有有效分割边中，找出一条最短的分割边，然后将该分割边与“形成该分割边的其他两条多变形边”形成一个三角形。此时就将凹多边形划分出了一个三角形。剩余多边形继续重新划分“分割边”，重复该过程即可。使用最短分割边的原因是，在概率上试图每次分出去一个尽可能小的三角形，以此增加最终分割的三角形的数量，进而增强分割后的信息量。

合并

在完成三角划分之后，就将一个多边形转换成了一些独立三角形的集合。此时在对这些三角形进行“合并”。合并是有条件的，合并后的多边形需要是凸多边形，配置参数“单多边形最大顶点数”控制合并后每个多边形能有多少顶点。

其实需求可以直接拆分成两部分，合并哪两个多边形（这里没有使用“三角形”，是因为本质上是多边形的合并，因为合并两个三角形之后，就形成了一个多边形）和如何区分合并后的多边形是凸多边形。

选择

针对第一个问题，选择所有可合并相邻多边形中”公共边“最长的两个多边形进行合并。所谓的“可合并”是因为，在第二步校验之后，有些不能合并的会被排除掉。至于为什么选择最长边，还是“伪贪心”思想，试图从概率上使每次合并的多边形更大，从而减少合并后多边形的数量，数量越少，后续的Detour算法越简单。

凸多边形校验

针对第二个问题，本质上，就是保证合并后的多边形所有内角不超过180度。此处采用的是”内角判断“。乐观的条件是，至少合并之前的多边形都是凸多边形。因为刚开始都是三角形，之后每次合并，都保证之前的合并是凸的。

校验两个凸多边形合并之后是否是凸多边形，思路概述（以上图为例）：

合并多边形BFE和多边形BCE，两者的公共边是BE，前提条件是，∠BCE和∠BFE都是小于180度的。问题是证明∠FBC和∠CEF在什么情况下会小于180度，在什么情况下会大于180度。

采用的方式是，连接CF作为参考线。CF产生的条件，从公共边两端点中选择一点B，点B在两个多边形中分别有两条边，选择不是公共边的那一条，即图中的BC和BF作为“校验边”，此时连接两条校验边的另外一个端点C和F，形成参考线。

形成参考线后，只需要保证公共边两端点分属在参考线的两侧，即证明以刚才选择点B所形成的内角∠CBF是一个小于180度的角。

然后再以公共边另外一个端点E重复上述过程，证明∠CEF是否满足条件。

反证法，理解上述方法的合理性（以下图为例）：

很明显两个多边形合并之后不是一个凸多边形，公共边是BC。用点B先来校验内角∠EBF。

当形成参考线后，发现公共边两点在参考线同侧。同时，点B，E，F三点可以形成一个三角形，三角形的内角一定小于180度，所以在三角形EBF中，∠EBF是小于180度的。

三角形EBF中的内角∠EBF恰好是合并多边形的一个外角。外角小于180度，对应的内角则大于180度了。

其实很好理解，用公共边一个端点和参考线一定可以形成一个三角形，只需要判断这个三角形的当前内角是合并多边形的内角还是外角就可以了。而当公共边的两端点在参考线两侧的时候，恰好对应的是内角。至于以公共边的两端点来进行这个校验，是因为我们保证了，合并之前的多边形都是凸多边形，意味着所有不参与合并的角本来就是满足条件的，不需要检查了，而参与合并的角，就是公共边两端点的角。

一定要理解：上述算法的所有思路，都是建立在合并之前的两个多边形都是凸多边形的基础上。

详细三角形

概述

经过上述过程，此时的场景信息已经被转化成了描述这些场景表面的“凸多边形”的集合——“Mesh导航面”。其实到这一步，整个Recast算法的任务已经完成了，导航面已经生成了，在Mesh之上就可以进行后续的所有基于业务的Detour算法了。比如寻路算法，射线算法等。

但是，回到“体素块”的定义。之前提到，在3D空间中，无论拆分单元的粒度有多小，都不可能完全拟合原实物空间，总是存在误差。而经过多步针对“体素块”的操作后，这些误差可能被放大，导致了Mesh导航面其实只是“原场景”的一个“大概表面”。比如楼梯。

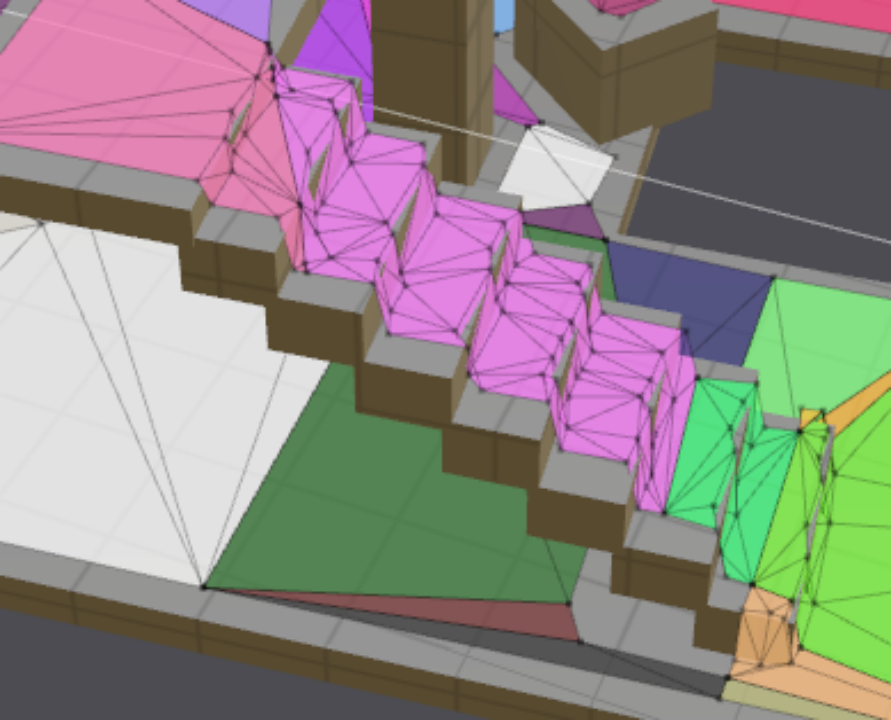
此时就需要，在Mesh多边形的基础上，去对比“原场景表面”，然后对Mesh多边形进行再加工——添加高度细节，使其最大限度的贴合原场景表面，减少误差。

注意，添加高度信息只是为Mesh多边形增加了新的额外的信息，无论如何操作，不改变原Mesh多边形的数据，两者在设计上解耦。因为高度细节只是让我们有更好的数据表示“原场景”的表面，但是仅仅是“更好”而已，体素化永远不可能完全拟合“原场景”的实体表面。但是在技术上，需要斟酌性能和内存方面的影响，过于优化从整体考虑，并不一定是必要的。

添加高度细节

这一步的优化分为两部分：先“优化边”，再“优化面”。

边

采样多边形边，根据配置参数“采样等分距离”在多边形边上进行“等分点”裁剪，获得“采样点”。

获得这些“采样点”在原场景面上“正竖直方向”对应的“原场景点”。

计算这些“原场景点”到多边形边的距离，找到最大距离Diff的“原场景点”。如果Diff大于配置参数“最大采样数据误差”，则认为多边形边偏离当前“采样点”对应的“原场景点”已经超过了允许误差，此时将这个“原场景点”添加到多边形边的“详细边点”中，并用原多边形的两个端点分别与之连接，形成新的多边形边。

以新的多边形边重复上述过程，直到所有“采样点”的“原场景点”都在允许误差范围内。

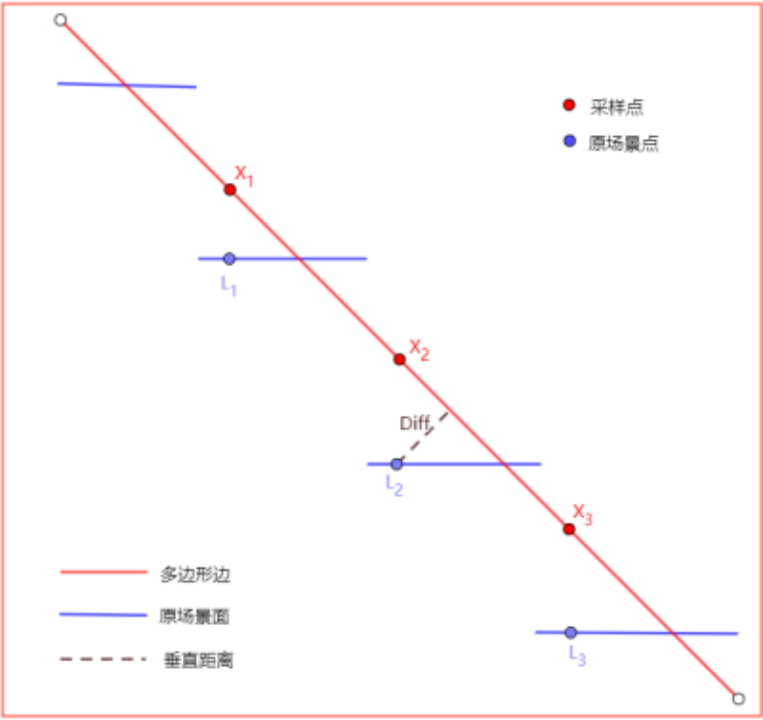
算法的本质与“简化轮廓”一致，都是试图寻找“离散点”的“平滑线”。需要注意的是，对于多边形边的等分粒度越小，误差允许范围越小，则优化后的多边形边就更贴合原场景，但是效率就越低。.

在得到更准确的多边形边后，对多边形再次进行“三角划分”算法。分割成三角形后，后续的“优化多边形面”是针对其内部的三角形进行的。

面

整体思路与“优化边”一致，只是从关注对象从边上升到了面。

先求出最小能包围“多边形”的AABB采样面，对采样面进行“二维矩阵”等大裁剪，生成“采样点”。

获取“采样点”的在原场景面上“正竖直方向”对应的“原场景点”。

计算原场景点到多边形中三角面的距离，找到距离最大的点，判断该距离与“最大采样数据误差”的大小关系。如果该距离大于“最大采样数据误差”，则认为多变形面偏移实际场景面过大，此时将该点添加到多边形详细点中，再进行三角化，形成新的三角面集合。然后重复上述过程。

至此，所有的体素化过程已经全部完成。其实，Recast注重的是导航面多边形之间的关系，这也为后续的Detour算法提供了重要的前提保证。

配置

可配置参数

数据结构

实体高度场

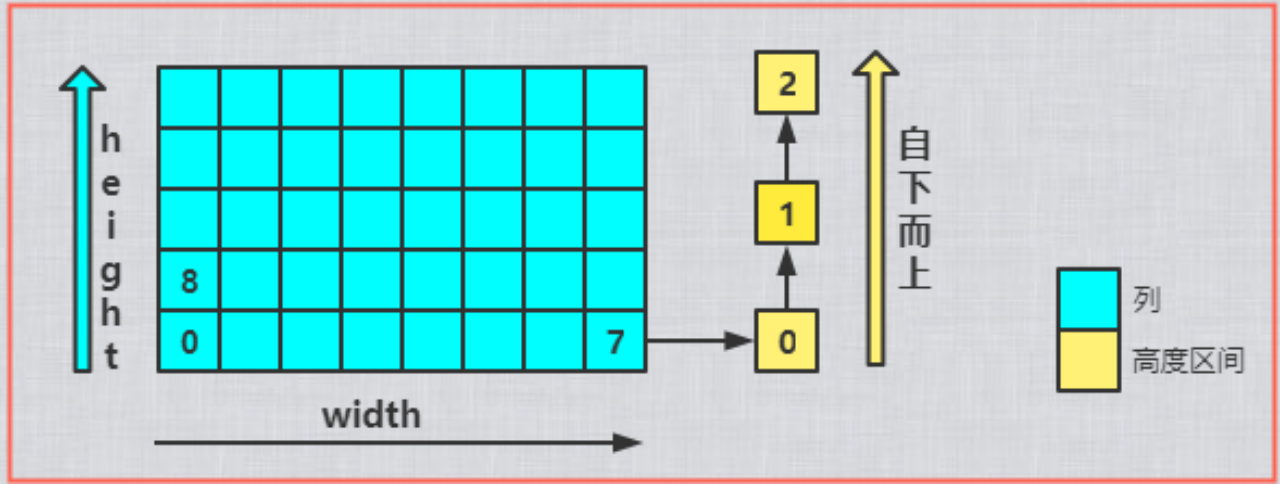
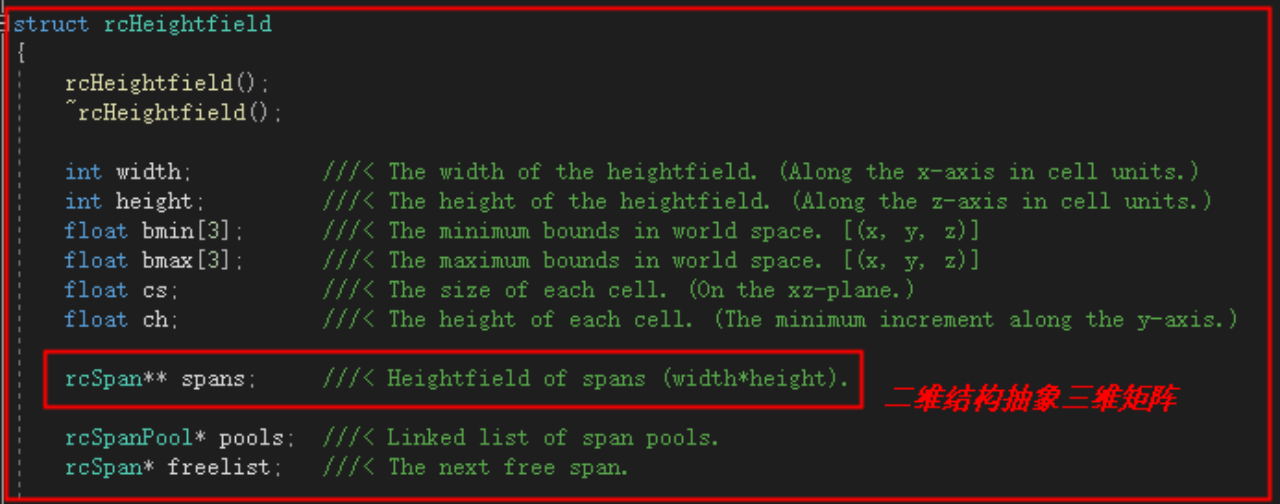
注意到Span中有一个area字段，该字段在体素化的这一步，作为上文提到的“是否可走”的特殊标识。

开放高度场

上文提到，无论是用实体高度场还是开放高度场，只是数据结构的不同，在逻辑上没有任何差别，Recast采用了开放高度场的数据结构进行体素化之后的所有算法。换句话说，再进行体素化构建实体高度场后，进行了一步实体高度场到开放高度场的转换。

注意，开放高度场是在整个体素化过程结束之后才转换的，此时已经经过了高度区间的合并和过滤，换句话说，其实此时实体高度区间的下表面已经没有任何意义了。至于为什么选择开放高度场，更多的考虑可能是Recast关心的是场景中的“无实体障碍可通过空间”，而不关心“实体空间”。但是需要理解，本质上，使用哪一个高度场并没有什么区别。

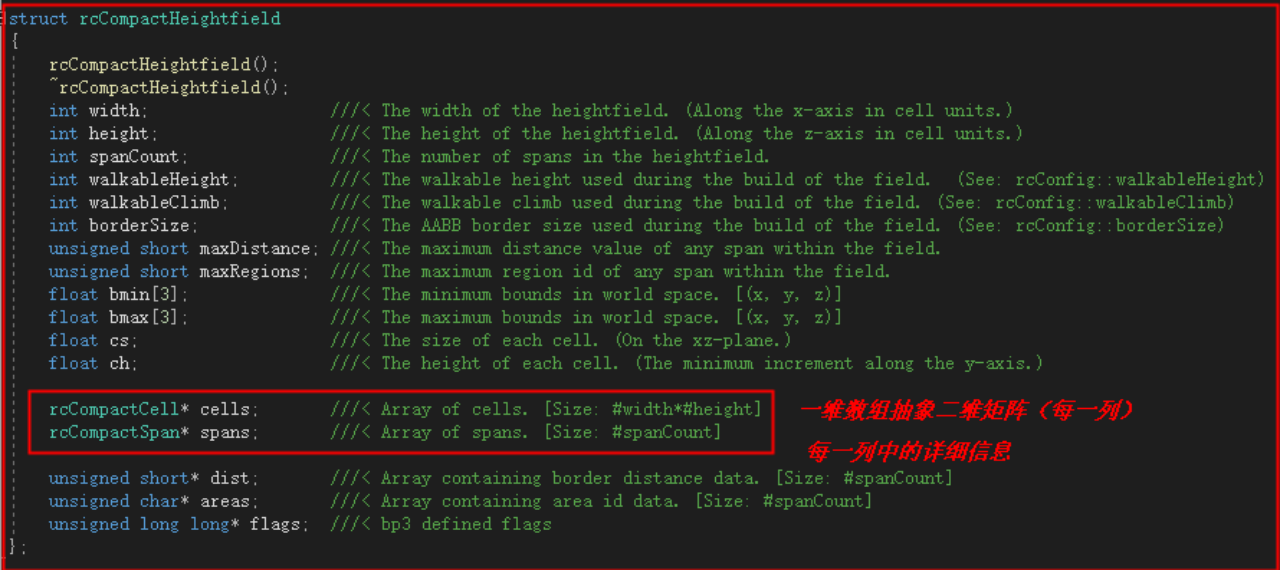
其中areas字段，就是实体高度场中对应高度区间是否可走的标识，其用一个一维数组直接标识了三维矩阵，其数组大小就是整个三维矩阵中所有Span的数量，索引序列依然是一列一列的依次排列。

Mesh—Tile

Recast将场景进行Tile划分后，会形成二维投影矩阵（实际是三维矩阵，高度维度由其他逻辑实现），矩阵的每一个元素都是一个Tile，注意tile本身并不是一个面，而是一个包含内部所有多边形的AABB包围盒（这是因为Tile内部的多边形并不共面）。Tile中维护了其在矩阵中的X和Y的位置，以及XY定位列中的序列。

项目应用

CS体系方案

在项目迭代、业务需求、技术支持等条件下，BP3从场景2D升级到3D，最终选择了一套Client-Server迭代的方案。

场景生成

前后端采用同一份场景obj文件烘焙出的同一份体素化数据，所有烘焙参数一致，体素化数据单独形成bin文件。然后再静态对bin文件加工，由recast后续算法生成Mesh多边形数据，再次形成并保留bin文件。服务器直接解析Mesh多边形的bin文件即可得到可用的场景导航数据。单独形成的体素化数据，则支持“动态阻挡”改变时对单个Tile的动态生成。

寻路相关算法

项目在寻路相关算法采用的是前后端独立的做法。前端负责“玩家”的移动以及其寻路，而后端负责依赖后端驱动的寻路，例如AI等。由于前端可以获取到更多的关于场景的详细数据，如场景点准确高度，所以前端的寻路相对简单。而后端在很多限制条件的前提下，采用了定制的寻路方案，下文详解。

资源管理

此处，只介绍BP3项目中，服务器对于场景资源的管理。约定，BP3中每一张地图的总数据称为“资源场景”，同一“资源场景”下的所有附属子集称为“逻辑场景”。例如，副本，位面。

所有场景数据的总路径如下：server\mmo.build\mmo.core\src\main\resources\map。

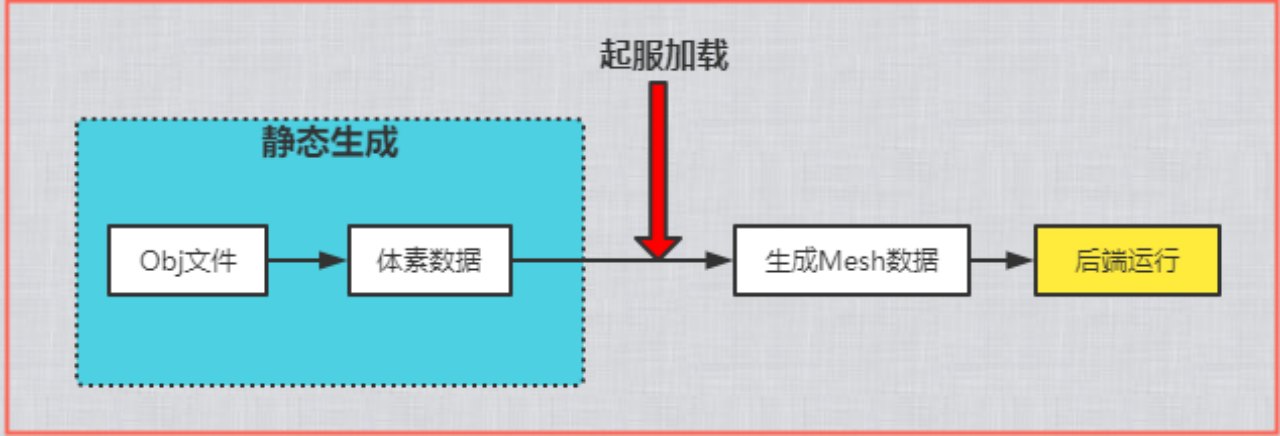
BP3中对于服务器端来说，并没有使用静态生成的体素数据，然后再去build出导航Mesh数据，而是让Mesh数据也静态生成，然后直接使用最终的Mesh数据，这将省去整个从体素化到Mesh数据的算法时间。但是，同时服务器也保留了体素数据，因为“动态阻挡”的实现还需要该数据。所以资源管理中其实有两份关于导航的数据，体素化后的体素数据，和静态直接生成的Mesh导航数据。

业务逻辑应用

包围盒

Recast支持三种类型的包围盒，分别是“圆柱体”，“AABB包围盒”，“OBB”包围盒。

圆柱体

AABB

OBB

静态区域划分

Recast支持一个“自定义区域划分”（Convex Volume）的功能。其可以自定义标识某些地方同属于一块区域，且可以被单独区分出来。例如，我们可以划分出一块区域，标识为“水”，那么在Mesh数据生成后，这部分导航面均会被唯一标识为“水”。

“自定义区域划分”是静态的，一旦划分出来，且设置了标识信息，其是不支持程序运行过程中改变的，也就是生成之后，就确定了。这为某些功能的实现提供了直接支持，设计中那些位置确定不变的静态场景物都可以考虑“自定义区域划分”的做法。比如，空气墙，静态障碍物。

具体做法概述：

在场景中构建“包围盒”，为包围盒设置标识信息，例如“水”。然后后续生成算法，会求解场景体素块与包围盒的交集，然后把这些交集体素块设置为自定义区域标识，这些标识会一直跟随到最后生成Mesh导航面。

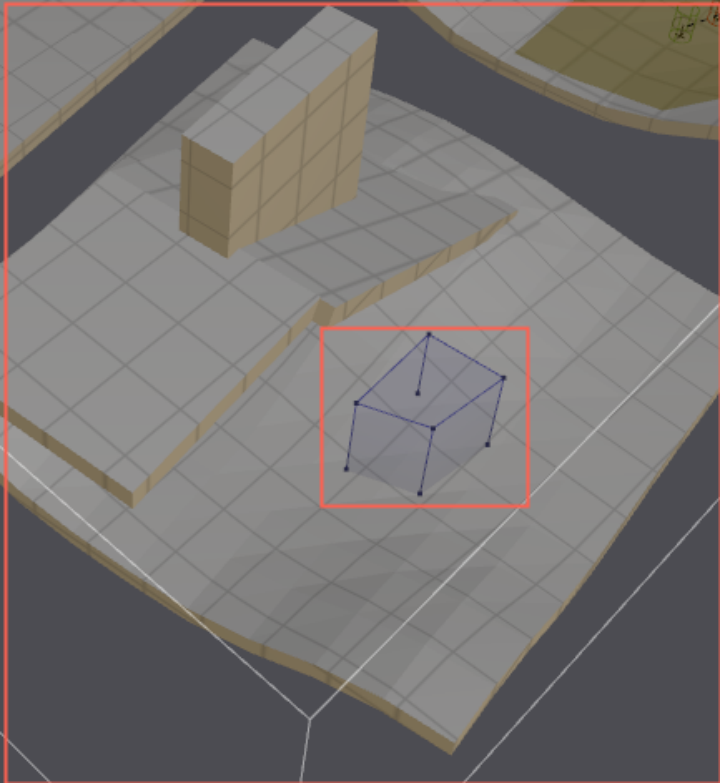
需要注意的是，这一步自定义划分区域标识，是在体素化之前完成的，其也不会改变原Obj文件，只是Recast单独维护了一份儿自定义区域的数据，在体素化的时候，会把自定义划分的区域标识给体素块，这也是为什么用一个包围盒圈起来空气墙，其实是求的包围盒和原实体场景相交的部分，将相交部分的体素块设置其区域标识。

空气墙

所谓的“空气墙”，那些位置不会改变但是状态会变化的障碍物。空气墙就像一个阀门，有开启和关闭的状态，同时也可以控制哪些场景物可以通过，哪些不能通过，等等。

“空气墙”需求的核心是，其并不能直接设置成阻挡，因为其有开启的状态。此时采用的方法是“静态区域划分”，利用包围盒圈出哪些地方是空气墙，将“空气墙”单独作为一片区域，并且该部分跟其他正常区域一样生成导航面，用过滤器控制属于“空气墙”的地方是否可以寻路等，以此实现所谓的开关。

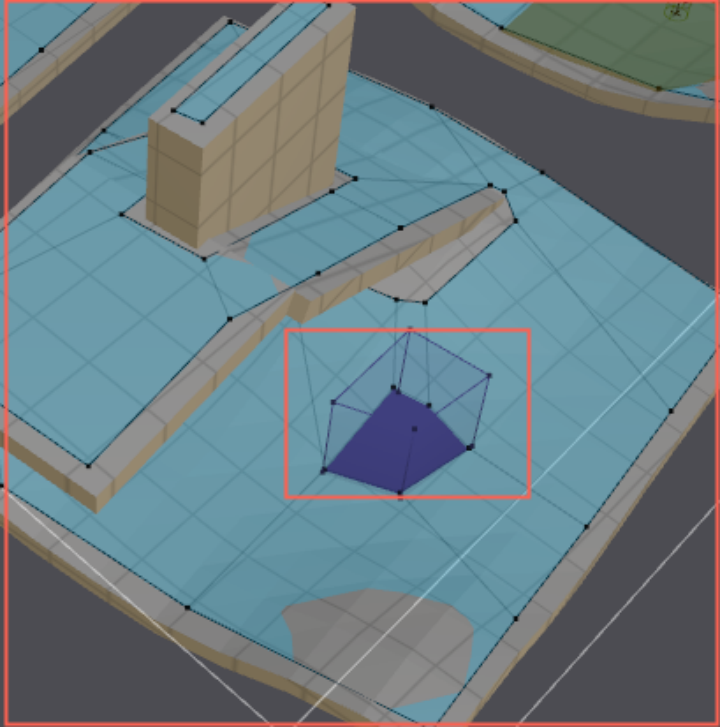
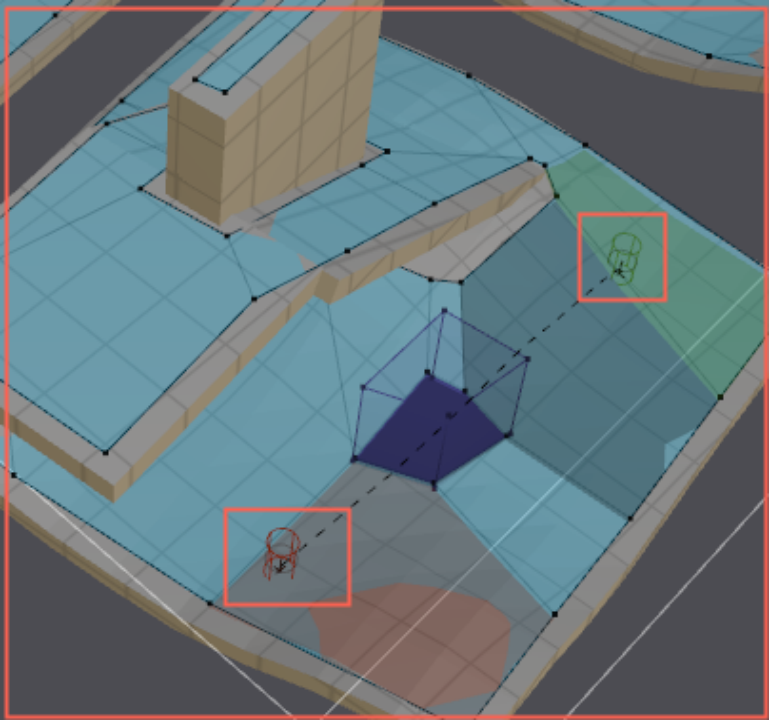
BP3使用了一个八字节自定义标识来标识空气墙。用定制的过滤器实现空气墙的具体业务逻辑，比如控制开关，控制势力值等。

第一位标识玩家是否可过：0是不可过，1是可过

第二位标识NPC是否可过：0是不可过，1是可过

第三到十位标识空气墙索引：空气墙Id = 场景id * 100 + 空气墙索引。

第11到32位是保留字段：预留参数位置，现无用。

第33到64位标识势力值：33位是势力值1,34位是2，依次类推。

逻辑区域

BP3的逻辑区域目前分为：“水域”，“安全区”，“BOSS区”，“禁骑马区”，“禁疾跑区”，“步行区”。所有逻辑区域的处理方案并不是一致的，“水域”比较特殊，同一资源场景下的所有资源共用一份儿数据。除了“水域”之外的其余逻辑区域，都是每个逻辑场景单独一份儿，因为他们之间可能有交叉重叠的部分。

注意，逻辑区域的本质和空气墙一样，属于自定义区域，且是静态的。

方法概述：

将当前场景以俯视的角度划分成X乘Y个格子。很明显，格子的大小决定了格子的多少。为每一个格子赋予数据，标识所谓的逻辑区域。

BP3采用八字节数据标识每一个格子，在3D场景中，逻辑区域的核心是，必须可以标识同一个格子中出现的多层高度不同的导航面的情况。

BP3采用了保守做法，最多只保留同一2D投影下的4层高度数据，依次用两个字节的数据标识。每两个字节十六位，高十四位是当前层的场景高度，后两位是当前位置是否属于该逻辑区域。

动态阻挡

所谓的“动态阻挡”，就是游戏运行过程中，出现变化的阻挡（障碍物）。考虑到BP3中会有类似的需求，所以无论是Mesh生成，还是寻路，都由此原因做出了很多必要的前提准备。例如，Mesh烘焙方式选择了支持动态阻挡的方式，寻路层面更是对此做了定制化的过滤器。

“动态阻挡”需求的核心点是，当在程序运行中出现动态改变的时候，如何去更新当前的Mesh数据。例如，盾兵（BP3中盾兵使用了动态阻挡）从A移动到了B，原来A是不可通过的，但是移动之后A可以移动了，但是B不能移动了。这就是为什么Obstacles烘焙方式，将一整张地图划分成了很多个Tile的原因，这样可以每次只关心出现变化的Tile，而不关心没有动态阻挡的Tile。

Detour算法

概述

简介

Detour算法就是场景中基于Recast生成的Mesh导航面而运行的一系列算法，并且Detour算法有很多典型的处理思路可以满足大部分游戏业务需求。一定要提前说明的是，虽然Recast实现了3D场景的体素化，以及相应的生成了描述3D多层可行走面的导航网格。但是，Detour中的多数算法本质是2D投影运算，其用多边形的连接关系实现了逻辑上的“3D”。这就直接导致Detour算法很多时候是有限制的，如果不能了解其原理和算法方法，可能在特定的情况会出现一些意想不到的“错误”。

服务器选型

BP3服务器对于Detour算法的应用主要是“AI”和“战斗”两个业务场景。主要涉及到的算法有：点的定位算法、A星寻路算法、路径平滑算法、射线探测算法等，其中还有很多小的细节算法涉及到大量的数学空间几何知识。

值的单独一提的是，BP3的寻路算法是定制的。其流程为：定位业务起终点位置、射线探测过滤不需要寻路的情况、基础寻路求解多边形路径、平滑算法优化路径、计算详细点实现3D路径。

定位多边形

概述

为业务层提供的所有底层算法的接口参数都是位置坐标，所以Detour算法中首先要实现的就是将坐标点定位到Mesh导航面内。下述是BP3基于业务定制的定位多边形算法，其与Detour算法会有需求上的不同之处，但是原理一致。

方法概述：

定位点在哪个多边形内，本质上是建立一定的搜索范围，查找所有在该搜索范围内的多边形。

计算点与多边形的空间位置关系，最终找到点在哪一个多边形内。

包围盒

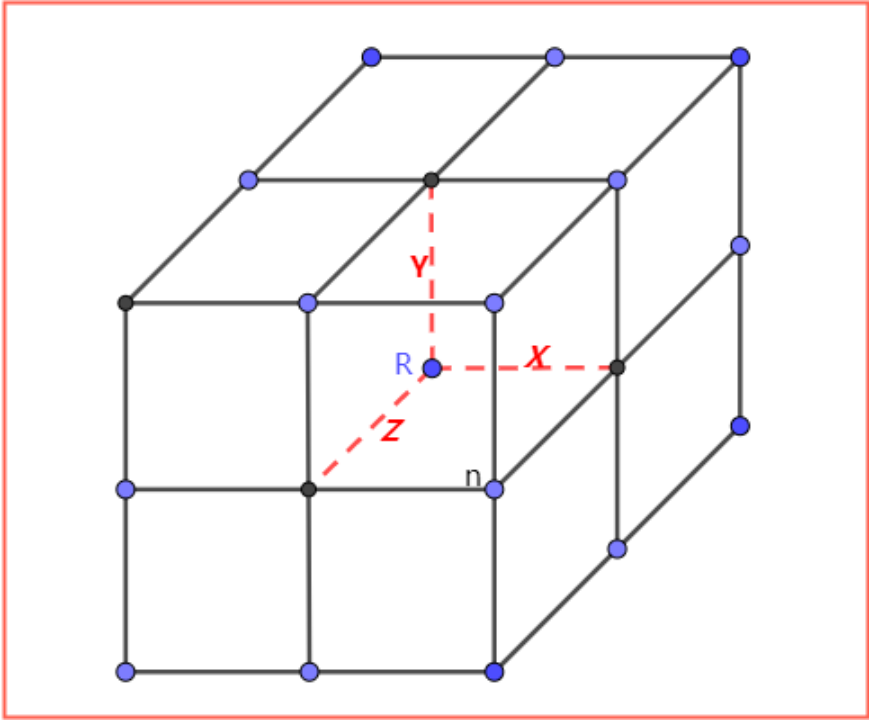
对于“构建搜索范围”这一步，采用的是以“坐标点”为中心构建一个AABB包围盒。相当于从“坐标点”出发，沿着“上下前后左右”六个方向搜索一定的空间。

该包围盒可以由业务层指定，设置三个参数，为各方向的搜索距离。

定位Tile

构建完搜索范围后，会查找哪些Tile处于该搜索范围内。

方法概述：

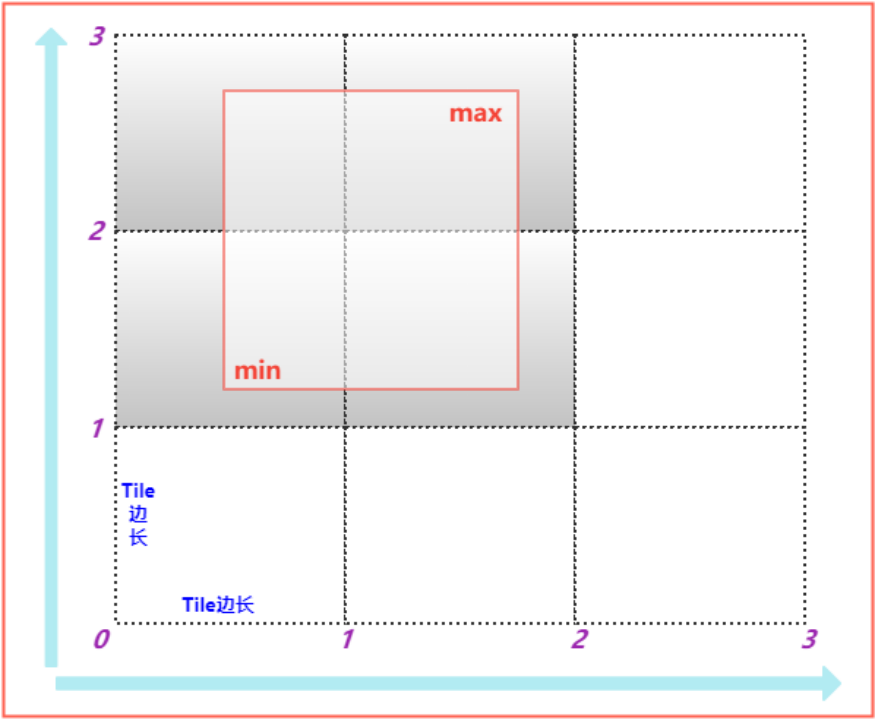
Mesh导航数据，会将场景划分成指定大小的Tile格子，并且维护每个Tile的逻辑编号。该逻辑编号的逻辑就是一个二维矩阵中元素的位置，此时，二维矩阵索引（逻辑编号）和坐标之间存在一个映射关系（Tile边长）。

“搜索范围”是AABB包围盒，所以很容易得到其空间最小位置点和最大位置点。

利用最小位置点min和Tile边长的比值直接定位min在哪一个Tile内，设Tile编号为（X_min，Y_min）。

利用最大位置点max和Tile边长的比值直接定位max在哪一个Tile内，设Tile编号为（X_max，Y_max）。

所有编号满足（X >= X_min）且(X <= X_max)且（Y >= Y_min）且(Y <= Y_max)的都在范围内。

上述介绍只是站在二维视角，实际搜索算法还需要加上高度范围的确认。

很简单，Mesh数据中对Tile的描述，Tile数据本身就是一个AABB包围盒（其内部多边形高度的最小值和最大值决定了AABB的高度），只需要校验刚才二维查找确认的所有Tile中那些高度在搜索空间范围内的即可。

有效多边形

筛选出搜索范围内的Tile后，需要定位这些Tile中哪些多边形处于搜索范围内。方法很简单，就是判断Tile内多边形的包围盒是否于搜索范围包围盒有交集。注意，无论是定位Tile还是定位多边形，都是求交集，而不是完全包含关系。

相交包围盒

这一步就完全转换成了求两个AABB包围盒是否有交集。而AABB包围盒的一个重要特性就是其有严格对称的空间临界点（最小点和最大点）。只需要证明一个包围盒的某个临界点在另一个包围盒临界点之内，就能证明两者相交。

很容易证明一件事，空间意义上即使多边形不处在搜索范围内，其包围盒也可能被计算在范围内。但是，对于算法来说，只是可能多了几个搜索的多边形而已。

BV树

定位有效多边形有一个非常有意思的情况，Tile很大，Tile内多边形很多的时候，应该怎么处理？还记得Recast的三种烘焙方式吗？如果是Solo Mesh的方式，整个场景只有一个Tile，那么在查找多边形的时候，难道要把所有的多边形搜索一遍吗？对于服务器来说，显然其性能和效率是不能接受的。

此时Recast做出的优化思路是，对每一个Tile内的多边形建立BV Tree的管理关系（其实本质上还是对Tile进行再次划分，从而实现快速定位），从而在查找多边形的时候更快的定位到可能处于搜索范围的有效多边形。需要注意这一步的意义是优化Tile内的多边形很多，遍历效率很低的情况。

BP3采用的多Tile划分的烘焙方式，且Tile大小有限，内部多边形数量有限且少量，因此，没有采用BV Tree的优化。其实基于自身方式的特点，优化意义也不大。

点在多边形内

经历上述的几个步骤后，此时已经粗略的找到了一定搜索范围内的多边形。此时，需要进行算法的核心，校验给定的“坐标点”具体处于哪一个多边形内。下面介绍两种具体的实现方式，Detour两种方法思路都给出了，但是其只实现了第一种。

两种方法，都是二维算法，均是在平面投影下计算的。

穿入穿出法

这种方法建立在一个数学结论下，大致概括为：“闭合多边形内的任意一点，沿着任意方向做射线，该射线相交于多边形边的条数必为奇数”。同理，如果点在多边形外边，那么射线相交于多边形边的条数必为偶数，因为“有进入必有穿出”，成对的。Detour中默认此方法实现。

方法概述：

首先要做的就是，对“坐标点”构建“射线”，Detour选择的就是水平线（任意射线都可以，越简单越好！）。

然后以此射线和多边形的每一条边计算相交关系，通过相交了几次，确认点与多边形的位置关系。

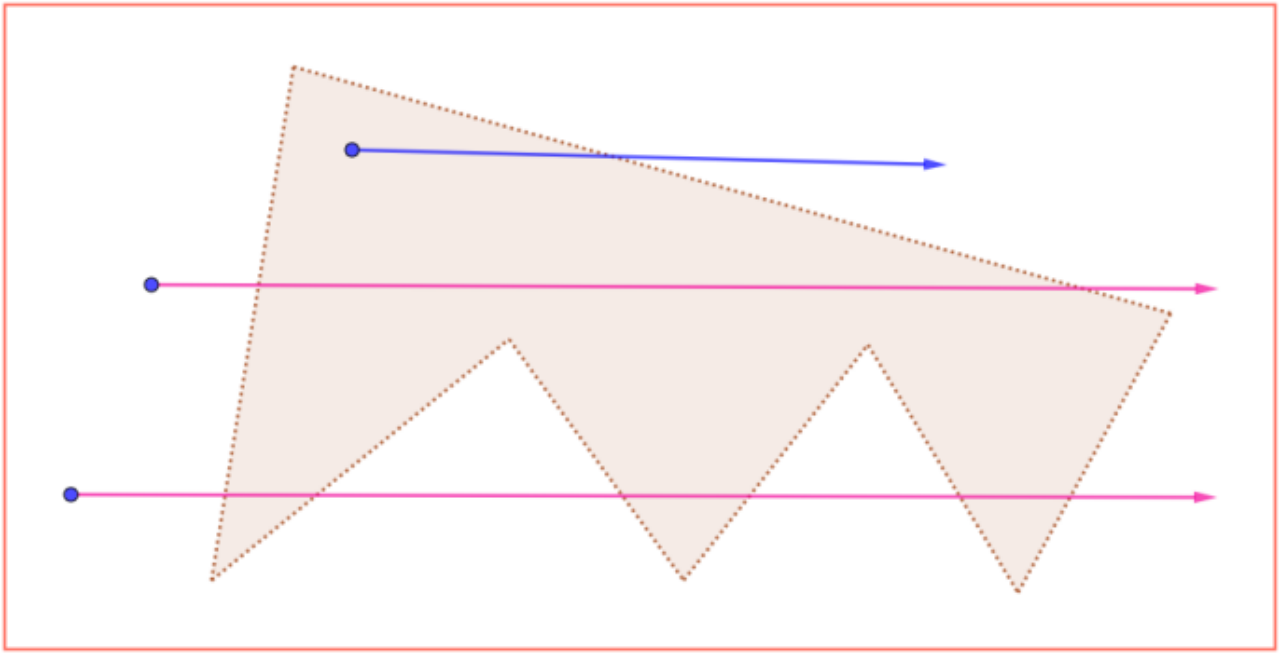
叉乘法

该方法是另外一种思路，同样建立在数学结论下，大概描述为：“一条直线可以将一个面分为左右两侧。而沿着顺时针或逆时针对多边形的每一条边进行左右划分，多边形恰好是所有边同侧区域的交集”。

方法概述：

沿着一个指定方法遍历多边形的每一条边，以逆时针为例。

将每一条边在上述方向下构建成有向向量a，起点A指向终点B。

以“边起点A”为起点，“坐标点Q”为终点构建一个有向向量b。

对每一条边的向量a和构建的向量b做叉乘，判断二者的位置关系，通过判断是否所有位置关系一致，来确认点是否在多边形的内部。

求解高度

上述已经计算到了“坐标点”在哪些多边形内，但其是二维投影下的计算。此时需要验证点是否在3D平面上。Detour并没有直接判断点与3D中平面的关系，而是直接求解在3D空间中，该点在对应多边形面内在竖直方向上的投影点。注意，此时的投影是沿空间绝对竖直方向的三维投影。因为之前已经判断了二维投影下点是否在多边形内，所以此时的这个三维投影点一定是存在的。

由于多层的情况，所以可能会出现与多个多边形的多个投影点，常规做法都是选取偏移距离最近的点，并将坐标点的高度修正为该投影点。所谓的偏移距离，就是“当前实际坐标点”与“三维投影点”的高度差。

那如何求解这个三维投影点呢？还记得Recast生成步骤中的最后一步吗？回忆一下，最后一步是生成详细三角形，目的是增加多边形内的详细高度信息（因为一个多边形所描述的原实际场景中可能并不共面），此时便派上了用场。

遍历多边形内的所有详细三角形，问题被转化为“求解点在三角形内的投影点”。

求解3D中点在三角形内竖直方向的投影点，方法概述：

数学定理，平面向量的基本定理，空间中任一向量可以由其他任意两个不共线向量唯一表示。a=λ1·b+λ2·c。其中b和c是两个不共线向量，两个系数只存在唯一解。

数学定理，三点共线的情况，当1中三个向量的终点共线时，有λ1+λ2=1。

算法思路基于上述两个数学定理，以三角形任一顶点A为起点，”求解点“为终点，构建”目标向量“。该向量可以由顶点A出发的两个边向量唯一表示。

此时的问题被转化成了，求解用两条边向量表示一个目标向量的两个系数。

这里有一个细节问题，既然向量可以由其余任意两个不共面的向量表示，那表示目标向量不是任意两个边向量就可以吗，为什么必须是顶点A出发的两个边向量呢？

这一步其实是有其实际意义的。因为”求解点“只会在其中一个详细三角形存在”投影点“。选择相同顶点可以进行一步过滤，当两个系数中出现负数，或者两个系数之和大于1的时候，证明点在三角形外。选择相同顶点避免了”线段“和”向量“之间的空间是否可以平移的差异性。

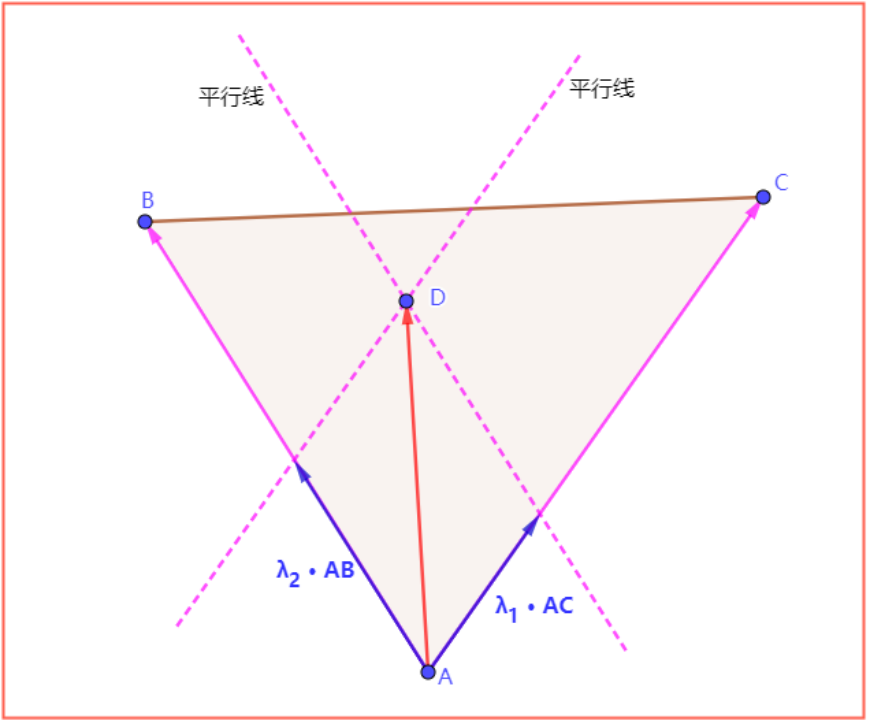
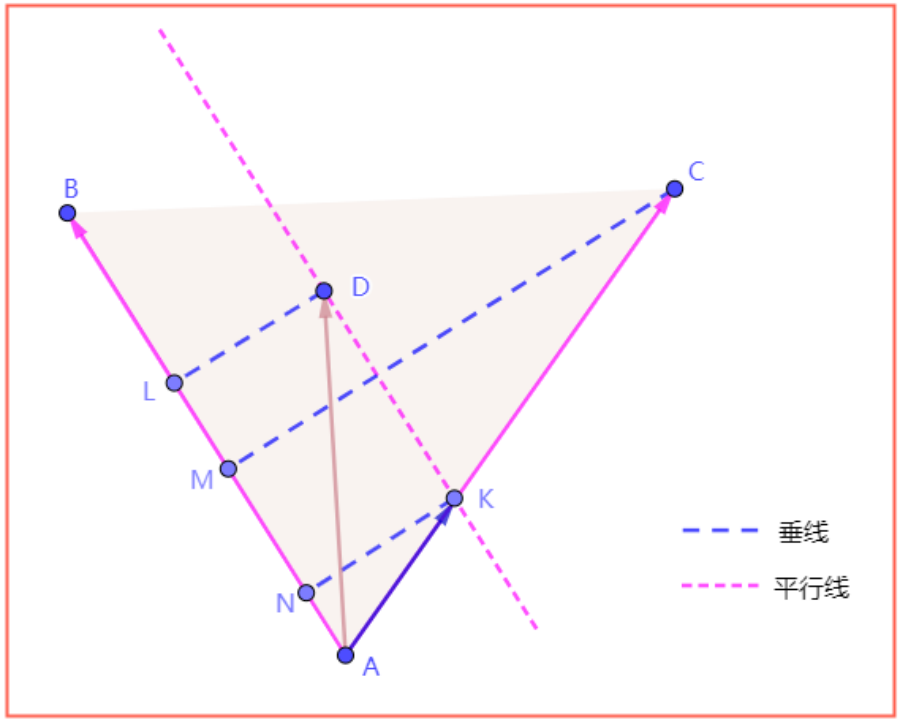
用两条边向量表示目标向量的两个参数求解，方法概述（以求解λ1为例）：

求解AK占AC的比例关系，由垂直关系转换为，求解NK占MC的比例关系。

求解NK占MC的比例关系，有平行关系转换为，求解DL占MC的比例关系。

而DL是AD在AB上的垂线，MC是AC在AB上的垂线，两个共端点线段在同一线段的垂线关系可以直接映射为彼此向量叉乘的比值。DL占MC的比例关系，可以转换成，向量AD×AB比上向量AC×AB（这里只是简单的介绍一下计算思路，实际计算涉及正负关系和标量矢量替换，下文有详解）。

射线探测

概述

算法目的

游戏中有这样一种需求，“两点之间是否可以在导航面内直接直线相连”，这种需求的解决方式，就是构建一条射线，求解沿射线方向，所经过的Mesh多边形。射线探测（Ray Cast）就是用来解决这个问题的。

”射线算法“目的概述（以下图为例）：

该图为俯视图，所有信息均为三维空间在底面上的二维投影。

算法的目的是检测起始点S到终止点N之间是否可以直线通过，并且求出射线SN所经过的多边形（下述称“路径多边形”），进而得到射线SN与路径多边形的相交边（相交边分为：“进入边”和“穿出边”），并且求出与每一条相交边的交点坐标（由于某些需求使用，该交点需要得到其三维信息）。如果点S到点N之间不存在直线通过，则需要求解出第一个不可通过的相交点。

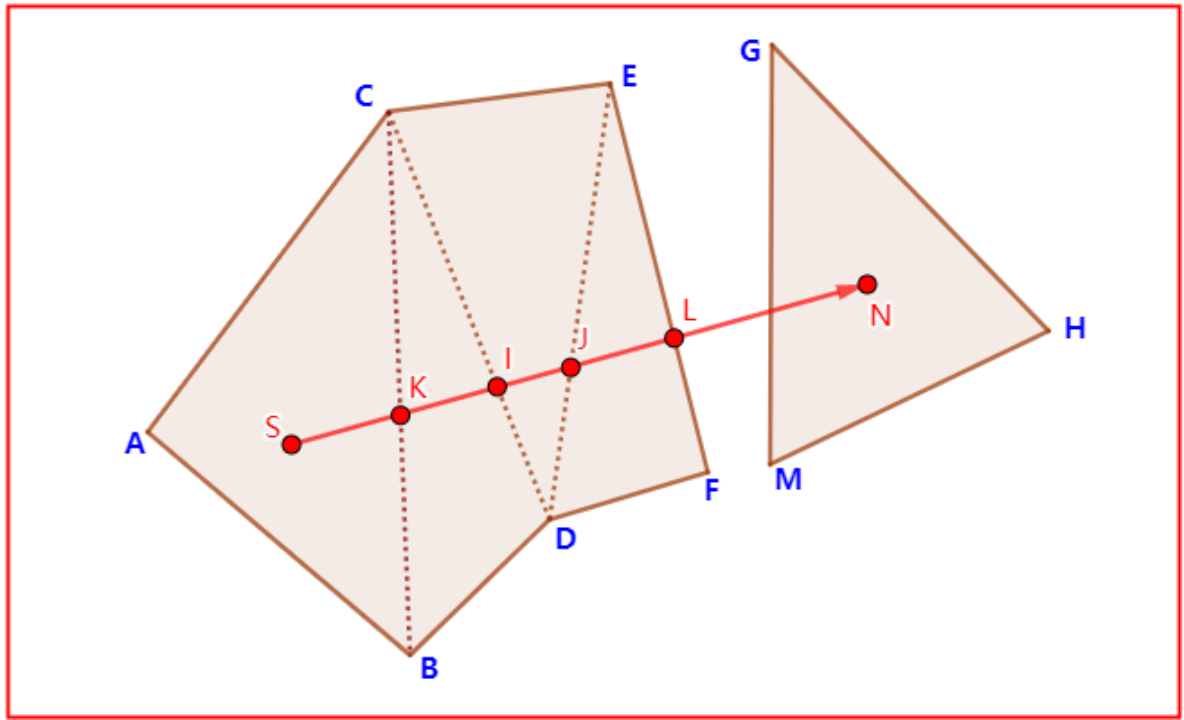
例如，三角形ABC、BCD、CDE、DEF均为路径多边形，边BC、CD、DE、EF均为相交边，且EF为边界边（非连通，没有邻居），点K、I、J、L为相交点，且L为射线探测的终止点。其中对于射线SN和三角形BCD，BC为“进入边”，CD为“穿出边”。

算法流程

该流程为Detour算法实现，BP3的实现原理和核心步骤与其一致，但是针对业务需求做了很多定制化处理，下文详解。注意，射线算法是纯2D的。

算法详解

射线算法的核心是，求解“射线”和“多边形”的“进入穿出”关系，也就是射线从哪一条边进入多边形（进入边），又从哪一条边穿出来（穿出边）。

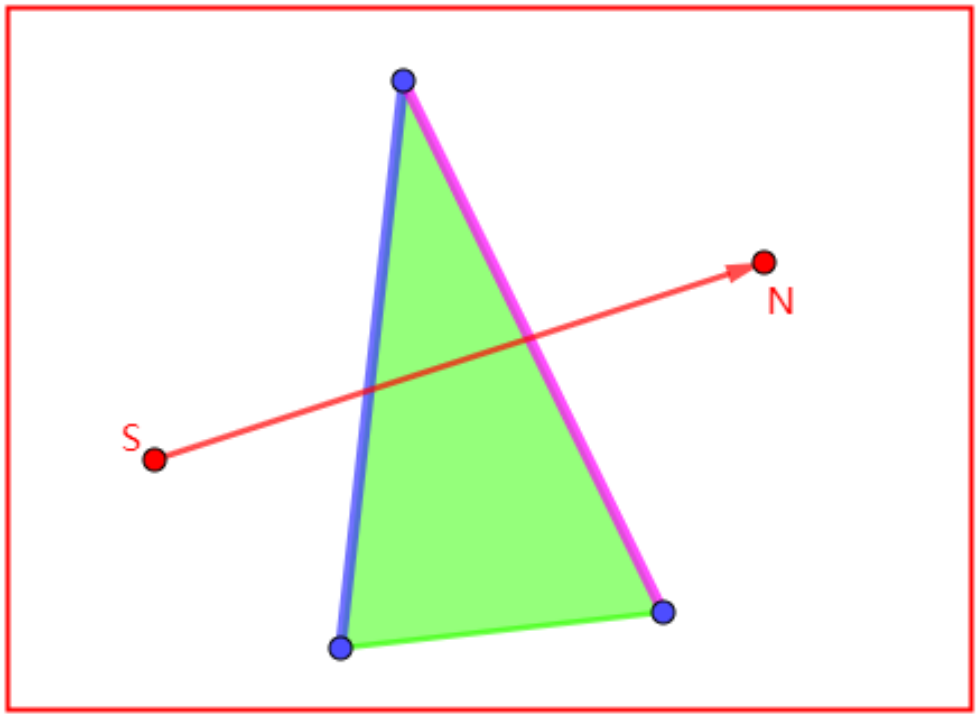
线段相交

很明显，算法的本质是，计算“射线”和“多边形边”的关系。而此时采用的方法是“直接求解两线段的交点情况，如果存在的话”。

求解两线段的交点情况，方法概述（以下图为例）：

求解SN和BC的交点K的信息，可以转化为求解SK占SN的比例关系，记为t。

SK占SN的比例关系，可以转化为，SS1占NN1的比例关系，因为△KSS1和△SNN1互为“相似关系”。

SC1是BC平移到同起点位置的向量，两者“等大同向”。

之前提到个这个问题，“两个共端点线段在同一线段的垂线关系可以直接映射为彼此向量叉乘的比值”。

所以SS1占NN1的比值，可以直接由其向量叉乘之比求解。

BS×BC = |BS|·|BC|·sinβ = |BC||SS1|。

SN×SC1 = |SN|·|SC1|·sinα = |SC1||NN1| = |BC||NN1|。

注意，上述两个计算过程是向量叉乘矢量运算，实际计算结果有正负之分，表达式只进行了标量运算。

可以确定的是，两线段有交点的时候，按照上述方法求解出的比值关系t的最终范围会在闭区间[0,1]内。但是需要注意的是，这一步是充分条件，并不是必要条件。也就是t的范围在[0,1]内的时候，两线段不一定有交点，下文详解。

线段不相交

上述是“两线段交点情况”的求解，那么自然需要一个新的问题，两个线段没有交点会出现什么情况呢？注意，平面内不平行的两条直线必有交点，所以线段除非平行，否则其延长线上必然存在交点。

交点在“起终点连线”的正向延长线上，此时，t值大于1恒成立。

交点在“起终点连线”的反向延长线上，此时，t值为负数恒成立。

交点在“起终点连线上”，但是线段不相交，t值也会在[0,1]内。

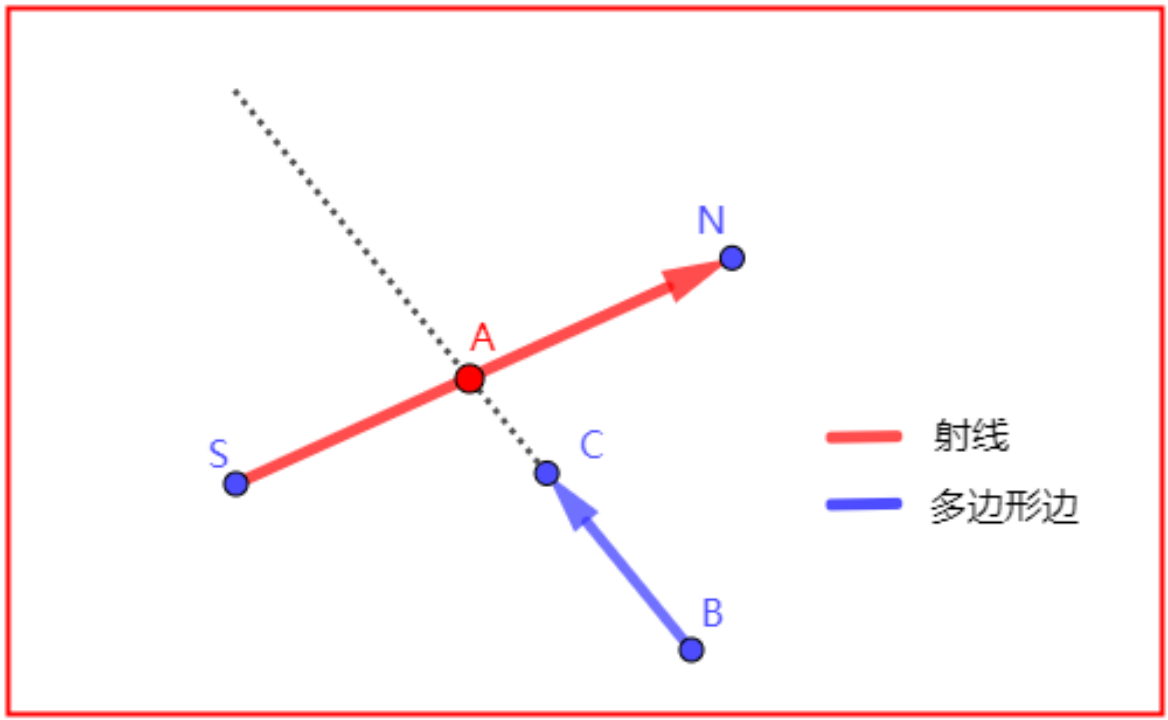
进入穿出关系

如果一条射线能够穿过一个凸多边形，则一定会有一条“进入边”和“穿出边”，寻找这两条边，就需要知道这两条边存在什么样的特征。当沿着固定顺时针或者逆时针方向对“多边形边”构建向量时，这两条边的向量和射线向量的空间位置关系是固定的。

逆时针时，“射线向量”必在“进入边”左侧（向量叉乘）。

逆时针时，“射线向量”必在“穿出边”右侧（向量叉乘）。

简单理解：

当所有边沿逆时针或者顺时针方向构建向量时，多边形内部恰好是所有边向量同侧区域的交集。

以逆时针为例，多边形内部区域一定在所有边向量的左侧。而多边形外部一定在所有边向量的右侧。

“进入边”恰好就是从“多边形外部”进到“多边形内部”，那“射线向量”一定是从“进入边”右侧到其左侧。

“穿出边”恰好就是从“多边形内部”出到“多边形外部”，那“射线向量”一定是从“穿出边”左侧到其右侧。

并且，当一条向量A从向量B的左侧穿向其右侧的时候，A一定在B的右侧。

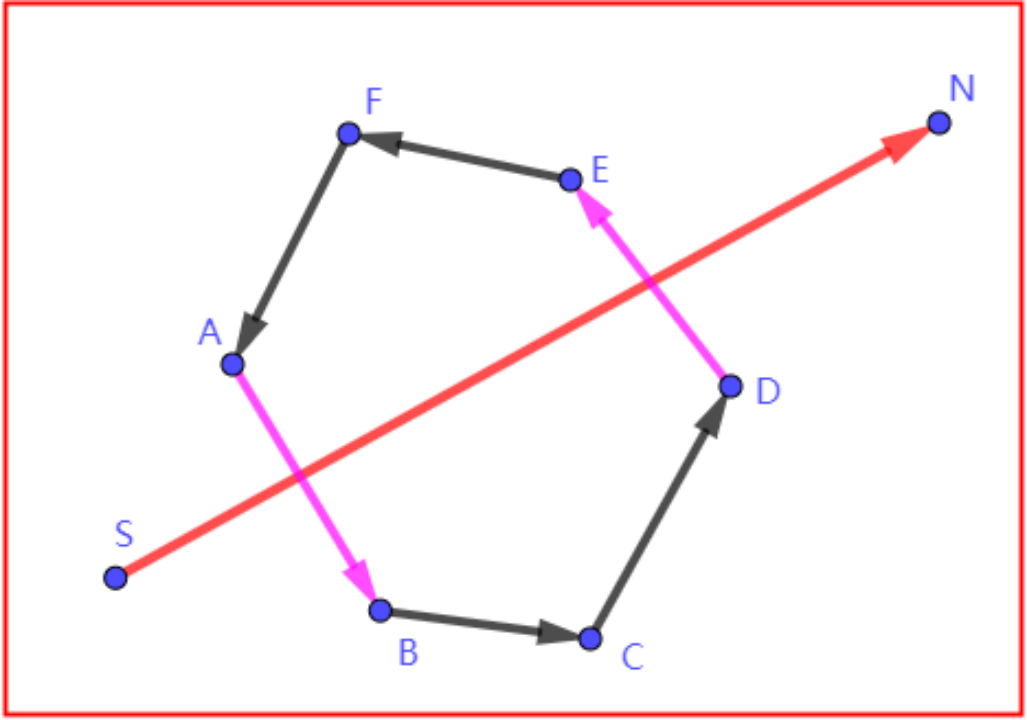
此时知道，当边向量方向固定的时候，“射线向量”一定在“进入边”的某一侧，这个位置关系是固定的。但是，这又是一条充分条件，而不是必要条件。也就是具有这种空间位置关系的边向量，不一定是“进入边”，当然了，其一定不是“穿出边”。

进入穿出边

此时总结一下上述结论，多边形边构建向量以逆时针（Detour算法）为例。

上述总结：

首先，计算出比例关系t，t不在[0,1]范围内的时候，边线段与射线线段没有交点。

其次，t在[0,1]范围的时候，边线段与射线线段不一定有交点。

最后，射线向量在边向量右侧时，该边一定不是“进入边”，可能是“穿出边”。

仔细分析上述结论，此时只剩一个问题了，怎么确认那些在[0,1]内的t值哪一个才是真正有交点的，哪些是没有交点不需要关心的。

所有可能是“进入边”的边中，t值最大的就是“进入边”。

所有可能是“穿出边”的边中，t值最小的就是“穿出边”。

简单理解，以下图为例（逆时针，观察“穿出边”）：

由于是逆时针，DE是“穿出边”，边CD和EF都在“射线向量”的左侧，一定不是“进入边”，t值在[0,1]内。

CD是“穿出边DE”前面的边（逆时针），与IJ的交点在其正向延长线上。

EF是“传出边DE”后面的边（逆时针），与IJ的交点在其反向延长线上。

恰好，逆时针的时候，“穿出边DE”的“前边CD”正向延长和“后边EF”反向延长都在（DE与IJ交点）的右侧。

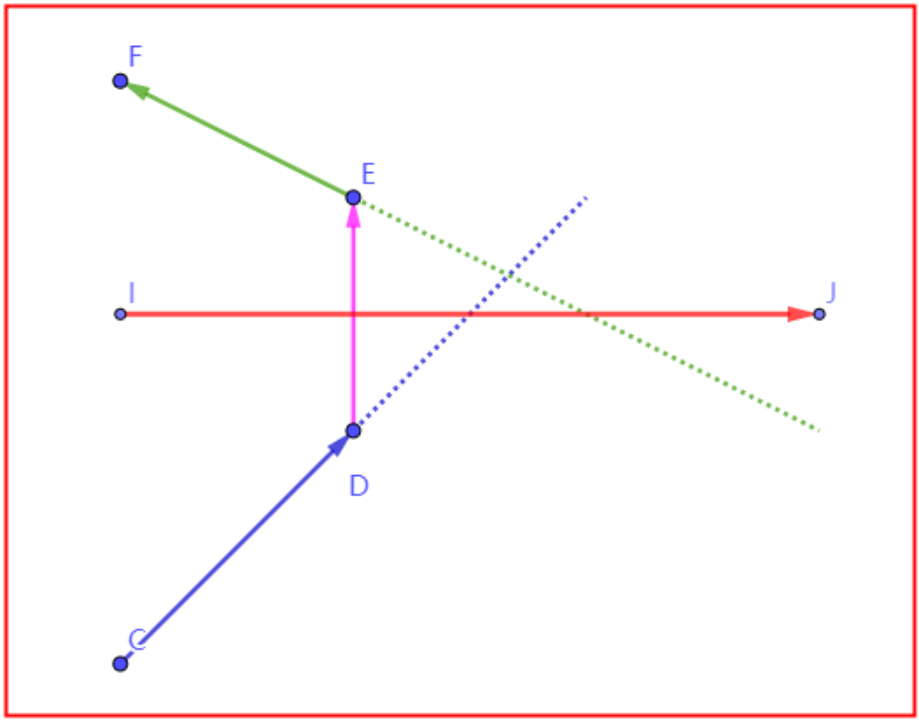
这两条结论的有一个非常大的前提，“起终点连线”必须与多边形有交点才成立。也就是说，必须有“进入穿出边”。射线算法本身自然满足了这一条件，因为射线算法过程中能够参与到计算的多边形都是有交点的多边形。

问题与优化

重复计算

回顾算法流程，算法不断的往前搜索需要与射线计算交点关系的多边形。而往前迭代的连接逻辑就是：找到射线与当前多边形形成的“穿出边”，那么与当前多边形以“穿出边”构成邻居关系的多边形就是，下一个要迭代的多边形。

这就证明了：下一个搜索多边形的“穿入边”就是上一个搜索多边形的“穿出边”。且是同一个交点，那么相应的t值就是一致的，这就是重复计算。

如果算法中是分开两次分别计算的这个t值。还会引起一个问题，t值本身就是一个比值关系，最后会被转化成小数，但是这个小数绝大多数情况下都是近似值，因为分数多数都是不能整除的。那么分开两次计算，很有可能造成两次结果有细微的不一致。

多层投影

我们一直在强调，Detour算法中大部分运算都是2D投影运算。射线算法也不例外，上述介绍的射线算法实现细节是纯2D运算，尽管所有的点都是3D的。

问题概述（以下图为例）：

注意，三个多边形均是实际存在的Mesh数据，不要理解成投影。S是射线起点，N是射线终点。

计算射线和多边形ABCD的穿出边是CD，多边形关于CD的邻居是CDEF。

射线SN与CDEF的计算结果是没有“穿出边”（2D运算），此时算法会结束。

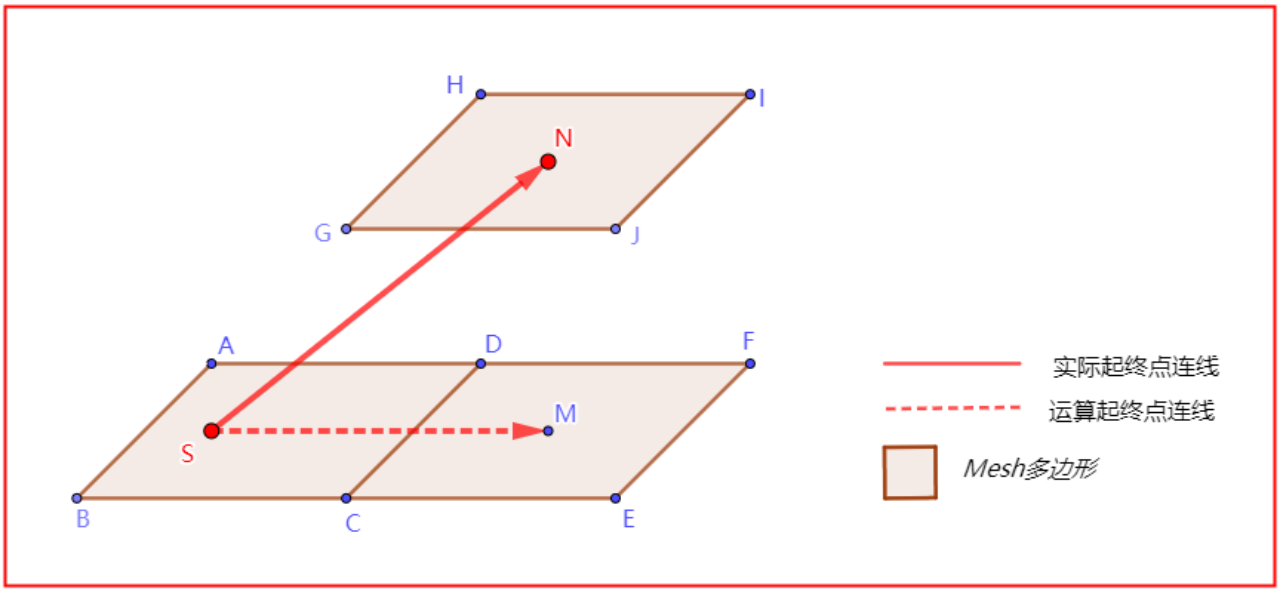
上述问题是，3D空间中的多层投影问题的2D运算带来的，该问题在实际应用场景中非常典型。解决思路很简单，判断实际终点的“多边形a”和射线算法结束的“多边形b”是否是同一个即可。

参考分析

数据结构

射线相关的只有两个核心的结果数据，分别是：射线算法的计算结果，起始点连线向量与多边形的进入穿出关系的计算结果。

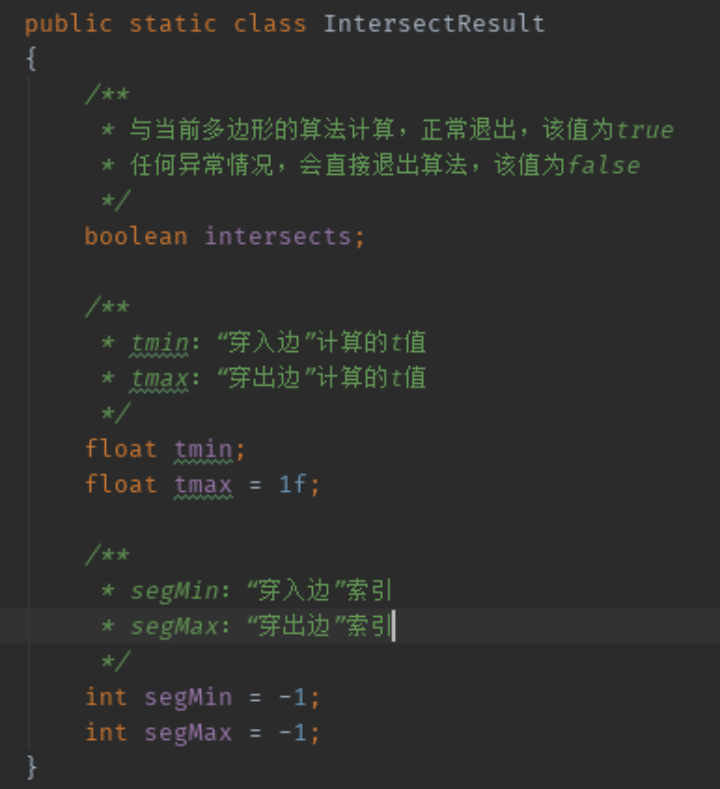
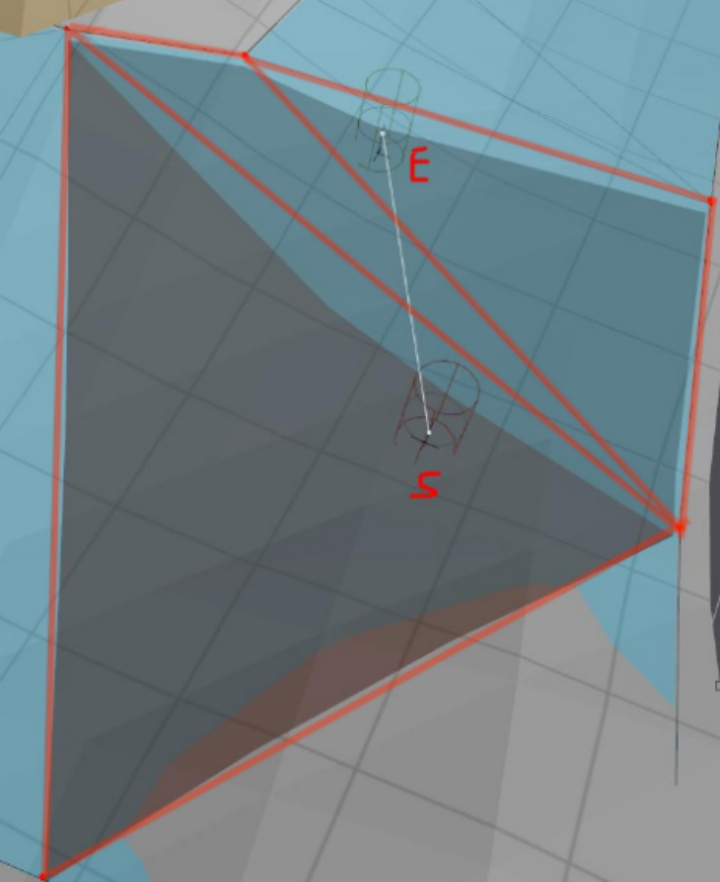
实例验证

此处只是以开源Detour的源码做一个简单的实例进行上述分析的验证，BP3项目中对射线算法进行了很多优化和基于业务的定制化修改。（由于相机视角不是正俯视视角，所以下述比例关系和视觉效果可能有偏差，属正常情况）。

寻路

概述

寻路是Detour算法的核心，也是整个Recast_Detour思想的出发点，所有的工作都是为了这一步，Detour作者更是花费了大量的时间和精力对致力于优化寻路的路径以及算法的效率。此处只是针对目前主流的启发式搜索算法（A-Star算法）提出一些优化思路，穿插简要介绍BP3中对于寻路的一些应用。

A星选型

选点

路径搜索算法是基于数学图论进行的，即无向带权图，本质是点集和两点连线距离。而Mesh导航面是“多边形数据”，如何选点来计算“多边形距离”对最终路径有直接影响，也正是因为这层映射关系，导致A星算法在游戏中不存在百分之百的最优路径，经过不断的优化，我们可以尽力的得到一条近似解。

多边形质点

这种情况是直接选择多边形中心（质心）作为“当前多边形的抽象点”，计算两个相邻多边形距离的时候，直接计算多边形中心的距离。这种方式，整体上直接将Mesh导航面转换成了“多边形中心”的无向带权图。

如下图所示，这种情况在实际应用中是效果最差的。

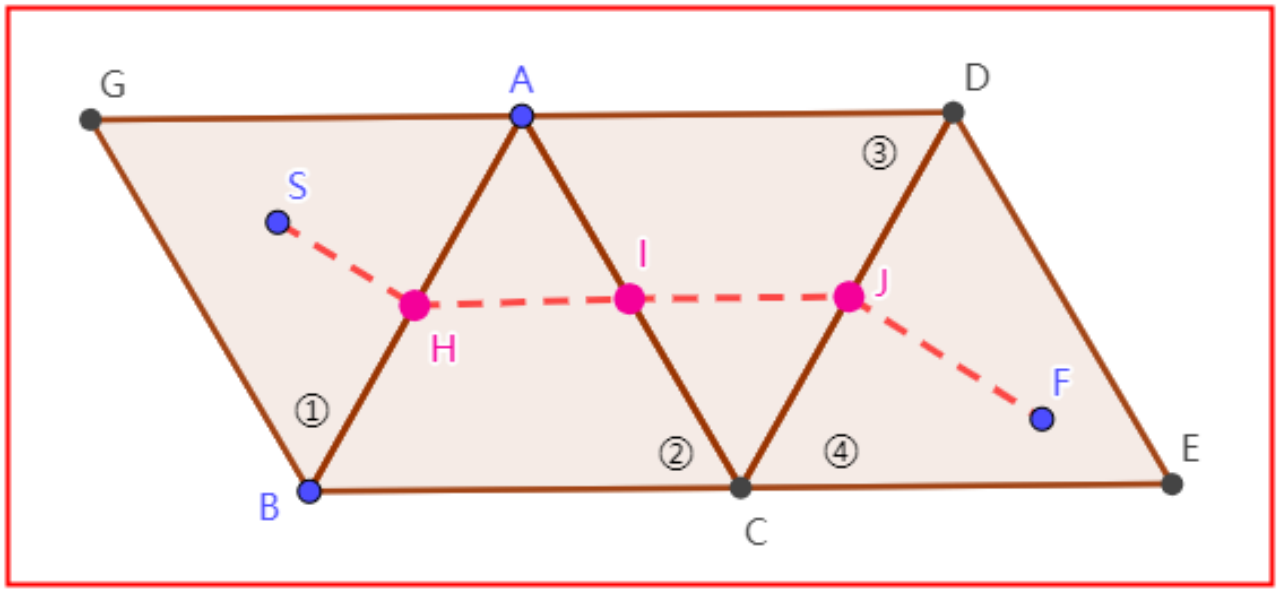
临边中点

这种选择以“公共边中点”作为从一个多边形进入另一个多边形的“抽象点”。如下图所示，从①中的S点开始，①②的公共边是AB，点H为AB的中点。以SH的距离作为从S进入到②的距离，同理，以HI作为从②进入到③的距离。

这种选择比选择质点效果要好，因为“在计算下一次距离的时候兼顾了上一次的距离”。从AB边进入②再进入③，和从BC边进入②再进入③的距离是不一样的，因此其在整体上有较好的表现。

但是，这种选择有一个致命的缺点，一旦出现“狭长多边形（最长边与最短边比值较大）”时，其寻路会很“怪异”。由于BP3选择了这种方式，所以上述介绍Recast生成的时候有很多参数选择都是为了减少“狭长多边形”的情况。

走向终点

这种选择稍微复杂，如下图所示，在计算某一个点到邻居多边形的距离时，其将当前点与终点连线SF，选择SF与公共边的交点（没有交点，以距离终点最近位置的端点来计算）作为抽象点。从S出发，S从①进入到②，选择SF与AB的交点作为其距离计算。这种选择类似一种实时更新方向，使其一直尽可能朝着终点前进。

这种选择，更耗费些性能（其实相差并不多，还记得射线算法中介绍的计算交点的算法吗？），但是其效果最好。这种选择还有一种变形，是以终点到公共边的垂点作为抽象点，但效果一般。

大世界分层

考虑大世界的游戏场景，如果寻路距离过长，A星搜索路径节点数将呈几何倍数增长，这对时间空间都是巨大的挑战，由此诞生了“多层寻路”思想。对大世界场景维护不同粒度的节点（比如Tile和Tile内的多边形就是两种粒度）。寻路时，先在大粒度层级上进行粗略寻路，然后在每一个大粒度内部进行局部寻路。

这种方式需要较多的信息管理，难点是必须维护“大粒度寻路节点”的联通关系，也就是“构建相邻大粒度节点的“双向门””，这个“双向门”不仅要求相邻节点节点间联通，还必须保证同一个节点的不同邻居间必须联通。

如图所示，从长距离S到N直接进行多边形寻路，效率太低。于是，先进行大粒度节点寻路，得到①②④，然后在每一个内进行局部寻路。其中①②和②④分别通过“双向门连接”，且对于②来说，其必须保证连接①④的两个“双向门”是联通的。

双向搜索

这种优化是一种“取巧”方式，其求解路径相较于“最短路径”偏差较大，但是能更快的找到一条可走路径。方法很简单，同时执行两个方向的路径搜索，从起点向终点启发式搜索的同时，从终点向起点启发式搜索，一旦两者互通，则成功。

很容理解这种搜索方式的速度，一棵大搜索树相较于两棵小搜索树，没有一点儿优势。（此处只是用树的概念解释，A星并不是树，但本质也是向前扩散搜索）。

优化思考

连通性

连通性是很有必要的一步，寻路算法在搜索的时候，会一直倾向于找到终点。有时候，起点到终点就是没有一条可达路径，这时候寻路算法自身会一直搜索下去，直到搜索完所有可搜索的区域，这会直接导致搜索节点暴增，且都是无意义的，严重的话甚至造成CPU完全限制在一次没有路径的搜索中。

连通标识

一个有效的方法是，为所有可搜索节点建立联通关系，类似于Recast生成中的区域。当我们生成Mesh数据后，对每一个多边形搜索其可达邻居关系，将其统一编号。例如下图左边区域设置联通标识为1，右侧区域为2。此时，如果从起点在1，终点在2，我们可以直接判断二者不属于同一联通区域内，即不可达。

搜索上限

为连通多边形标号是很有意义的，但是其有一个缺点，当有类似于“空气墙”、“动态阻挡”这些可以变化的数据时，往往会改变其连通性。并且，不像动态阻挡，其可以把影响范围缩短到一个Tile内，连通区域的动态变化往往影响范围较大，维护成本较高。

还有一种简单的常规方法，直接设置寻路搜索算法的最大搜索次数，这是一个“经验值”，过小或过大都有其弊端，需要依附具体业务场景进行设置。

启发式权重

深刻理解启发式搜索中的“启发函数”对于算法应用是很有必要的。

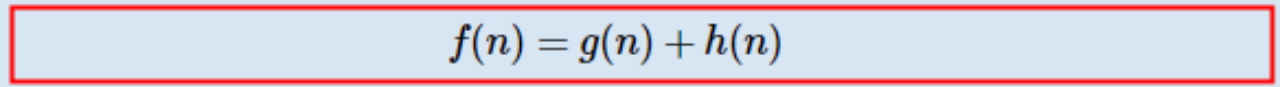
F可以理解为优先级，下一次需要搜索哪一个节点（A星中维护F的数据结构通常是优先级队列）。

G是从起点开始，经过路径迭代到当前搜索节点的距离代价，G是一个“实际值”。

H是从当前搜索节点到达终点的“预估距离”，这就是启发函数，H是一个“理论预计值”。

该式子进行简单的变形，F = a·G + b·H。为每一个计算式添加权重因子。

H就像一种牵引力，b越大，相当于越注重“距离终点距离近的节点”，也就倾向于先搜索距离终点近的点，这就相当于一直在朝着终点搜索。

相反的，b越小，就意味着“启发函数比重越小”，牵引力越小，越倾向于算法退化为”无启发搜索“。

使用对权重因子的控制来实现对路线的控制。当业务需求要求寻路尽可能从“游戏主路”通过，而尽可能不经过“水域”，尽管“水域”是可走的。此时就可以增大“水域”的启发式权重b，这样在逻辑就将“水域”设置成了优先级较低的路线，（当然也可以直接将水域的F值权重增大）。

路径平滑

概述

算法目的

以简单的多边形寻路算法路径为例，最终的路径点集是基于多边形边的，很多时候其路径点会呈现一种“左右摆动”的状态，且会显得很“松弛”，而我们希望最终的路径应该是尽可能直线，减少转向次数的。

算法流程

Detour采用的是“漏斗算法”进行路径平滑的，该算法也是纯2D算法。

算法思路

方向范围

上层寻路算法会找到一条多边形路径，依次经过这些多边形就可以从起点到达终点。这条路径中，相邻多边形之间存在公共边，而想要从一个多边形沿直线进入到另一个多边形就必须经过这条公共边。这就说明，从某个多边形内一点沿直线移动到其邻居多边形内是有方向要求的。

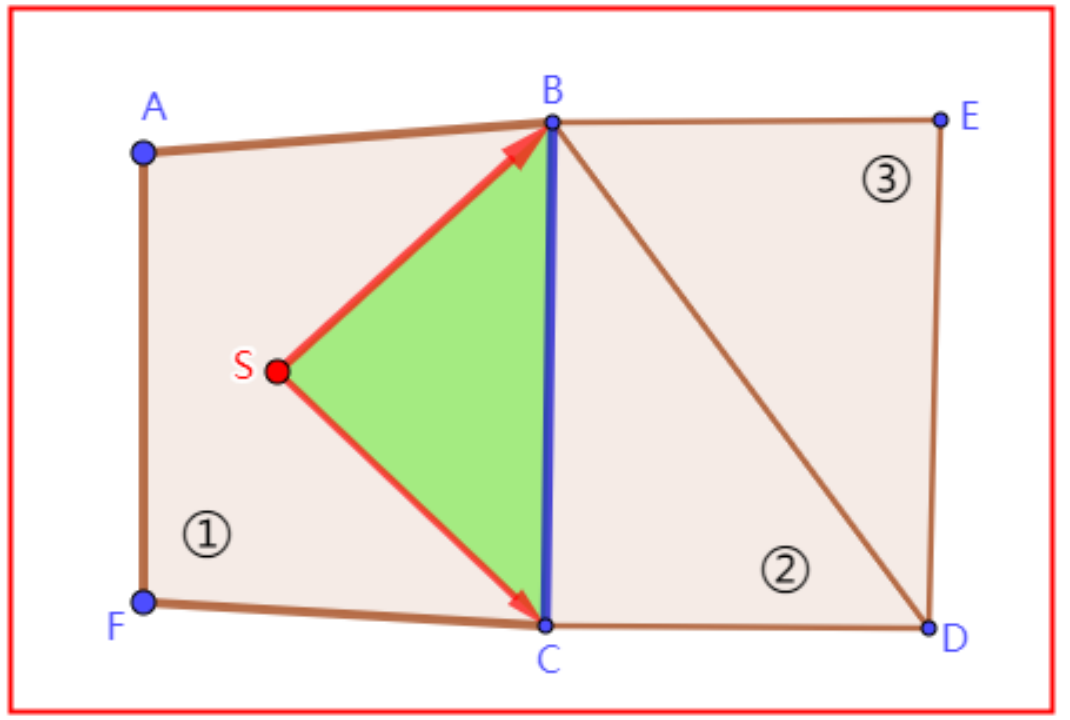
如下图左图所示，S从①进入到②的直线移动方向，只能是射线SB顺时针到射线SC的范围内。同理，如右图所示，从S进入到③的直线移动方向，只能是射线SB顺时针到射线SD的范围内。

范围交集

如下图所示，从S出发沿直线进入到②，“方向范围”是SB顺时针到SC。从S出发沿直线进入到③，“方向范围”是SF顺时针到SE。此时很容易得到，如果我们想从S沿直线经过②到达③的“方向范围”是什么呢？就是两个“方向范围”的交集，因为需要同时满足进入②和③的方向，这很容易理解。

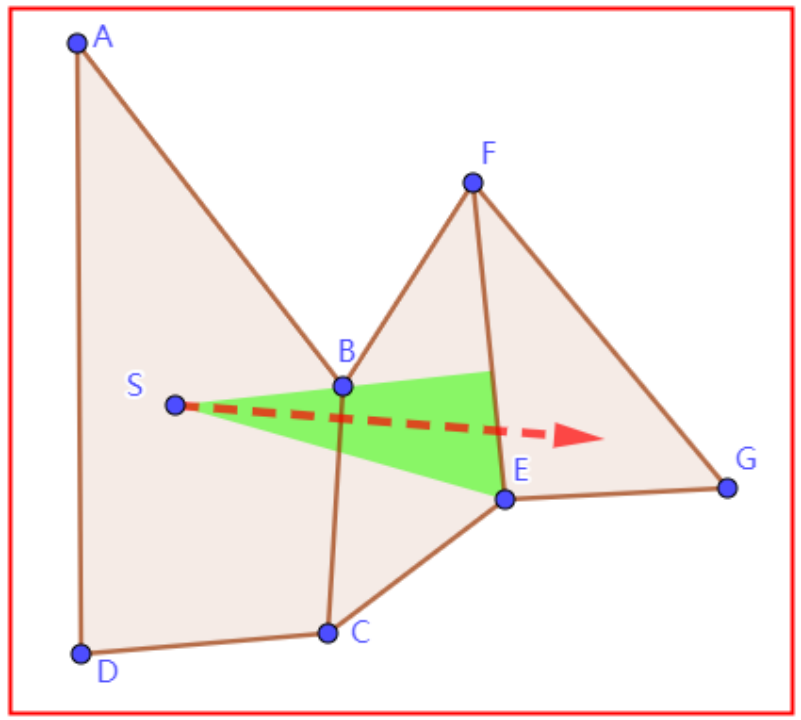
拐弯

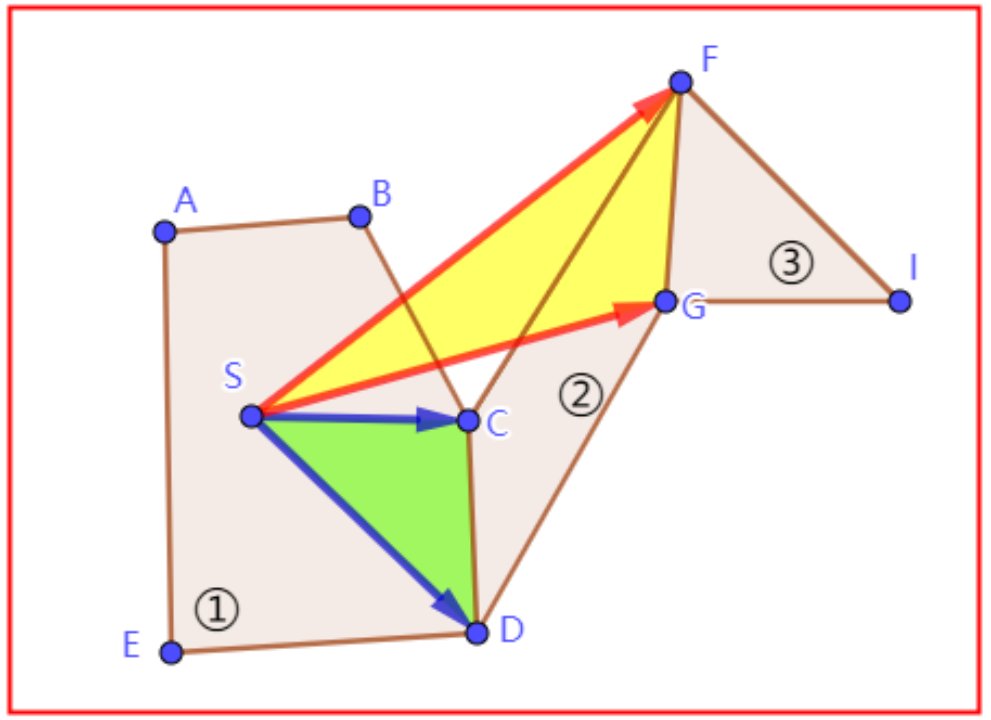
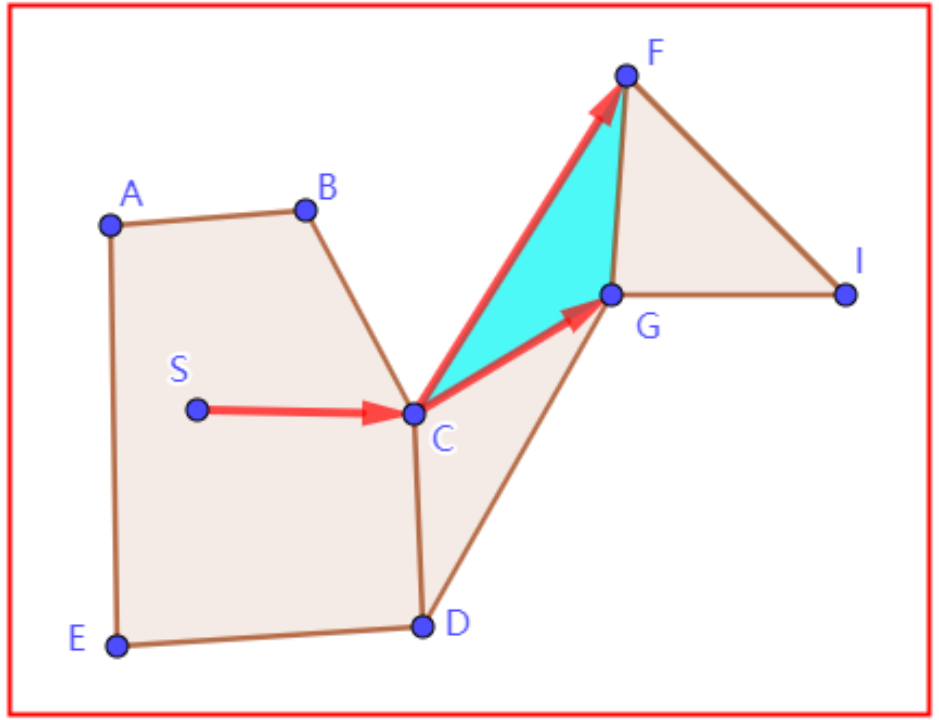
上述介绍了“方向范围”有交集的情况，那必然存在没有交集的情况。如下左图所示，从①到②的“方向范围”，和从①到③的“方向范围”没有交集。这直接说明，从S点没有任何一条直线路径可以经过②再到达③。那么此时，只能是先沿直线走到②，再考虑从②开始，之后的直线路径情况，这就是“拐弯”。出现拐弯情况的点，在“漏斗算法”中被称为“拐角点”，如图中的点C。

注意，出现拐弯时，以拐角点作为新的起点，考虑之后的“方向范围”情况。

漏斗详解

上述“算法思路”中，详细介绍了“沿直线进入下一个多边形对于方向的限制”，而通过不断的迭代，方向范围的交集会越来越小，或者出现拐角点。这也是算法名称的由来，“漏斗算法”、“拐角点算法”、“拉绳算法”。很显然，算法的核心是计算“点沿直线进入不同多边形，其对应方向范围的交集”。

公共边

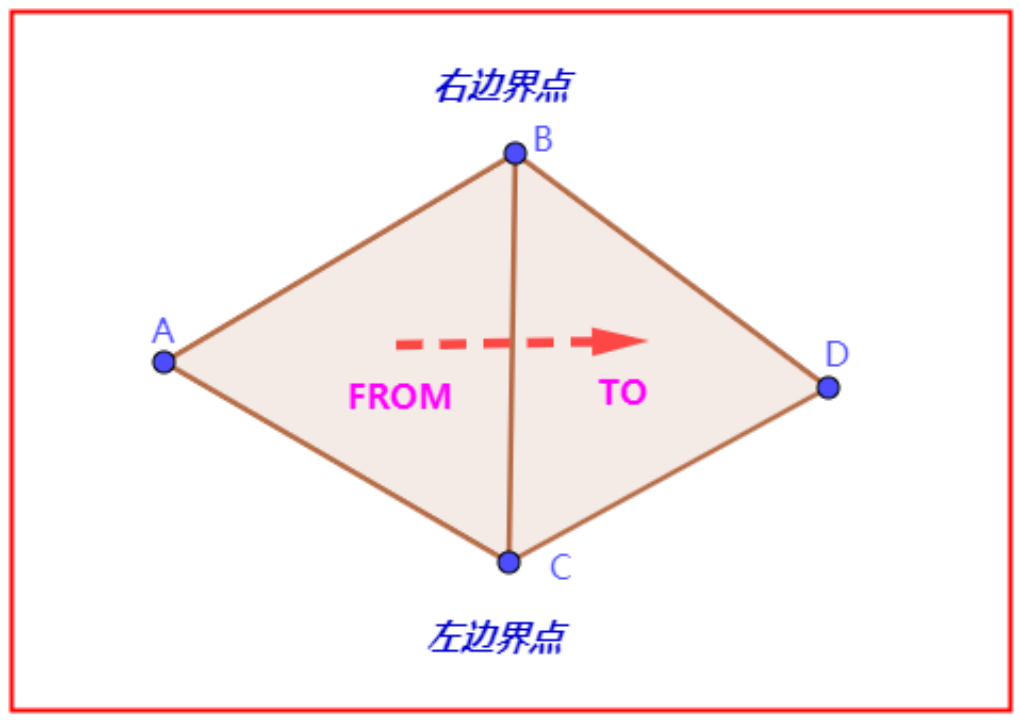
约定，从一个多边形a经过公共边到另一个多边形b，称a为“FROM多边形”，称b为“TO多边形”。其公共边在“FROM多边形”沿逆时针方向从点C指向点B，称点C为“左边界点”，点B为为“右边界点”。

此约定以Detour算法为准，没有任何逻辑意义，只是为了说明算法。

交集关系

漏斗算法的核心就是去找“新边界”和“旧边界”的交集。新边界就是迭代到当前多边形与其下一个多边形公共边形成的边界，算法起始从起点开始寻找其邻居多边形。当形成拐角点后，以拐角点作为新的起点，重复这个过程，直到迭代结束。

计算包含关系，就是对两个边界进行空间位置的判断，向量叉乘即可。图中，红色实线为旧边界，蓝色虚线为新边界。约定，逆时针由左边界到右边界。

包含关系

新边界都在旧边界内，或者旧边界在新边界内，以小范围为交集。

部分相交

一条新边界在旧边界内，一条在旧边界外，求交集。

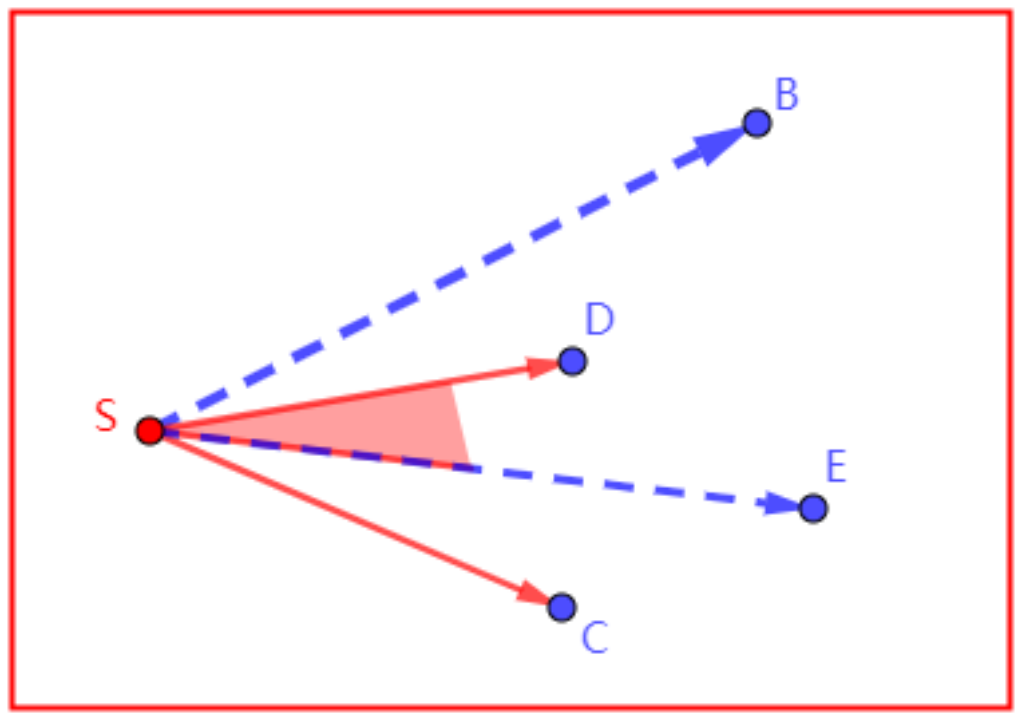
不相交

新左边界SE在旧右边界SD外，或者新右边界SB在旧左边界SC外，无交集。

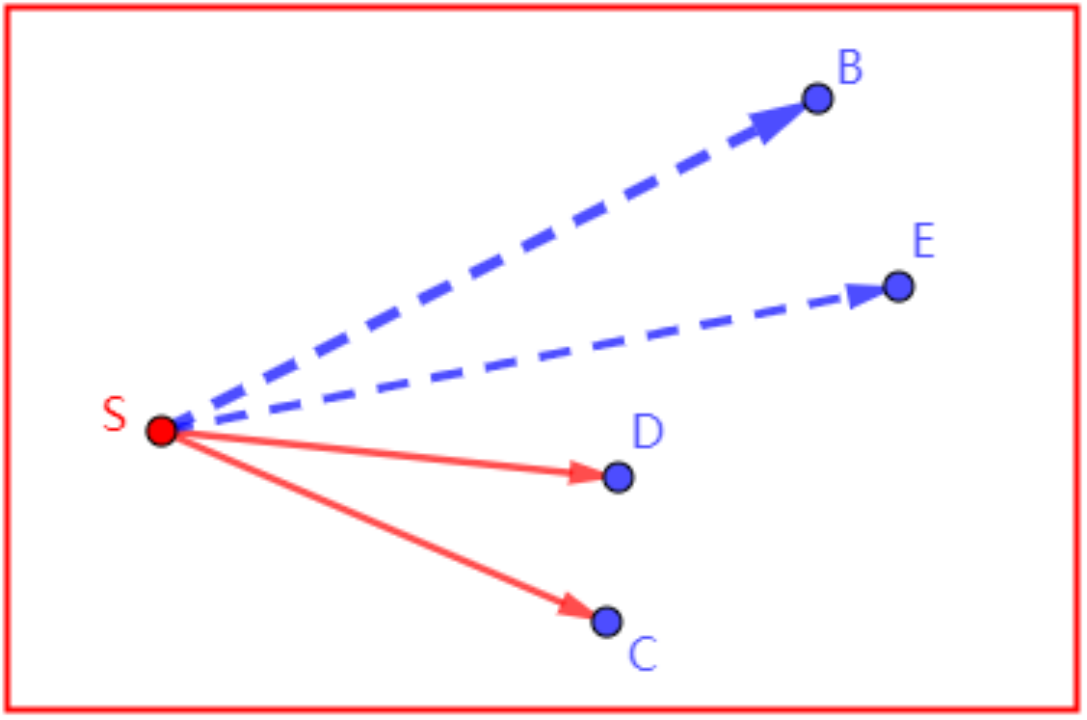
算法思考

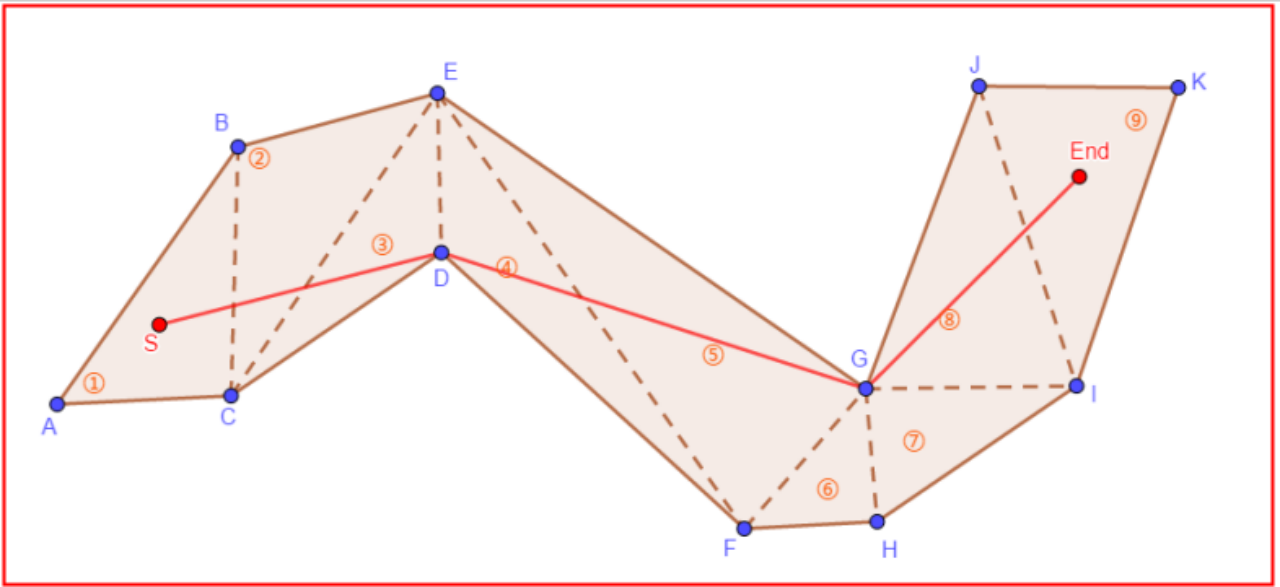
了解“漏斗算法”后，一定要理解，漏斗算法是完全基于上层寻路算法的查找路径的，它自身没有任何逻辑处理不在上层寻路路径中的多边形（当然了，可以基于此做出定制化修改）。

观察上图，标号①到⑨是上层寻路路径，红色实线表示“漏斗算法”平滑后的路径。可以发现，即使紫色标识的多边形CDF是可通过的，由于其不在上层寻路路径中，SG本可以直线通过，却被限制在了SD到DG的一次转向中。

问题的本质，并不是“漏斗算法”的问题。当遇到此问题的时候，应该考虑上层寻路算法的问题，一个好的寻路算法在寻路的时候就应该尽可能将CDF加入到路径中。但是，正如寻路算法的介绍，我们只能尽可能的避免这种情况，导航网格的寻路，就是多边形到点集的抽象，不存在百分之百的正确。

详细路径

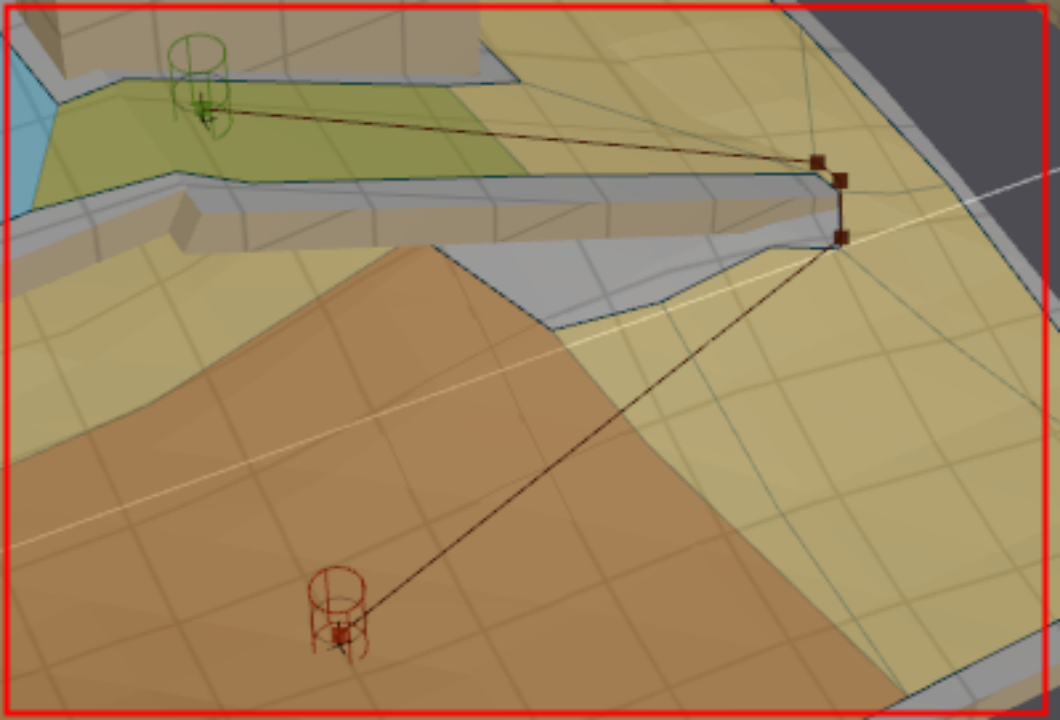
到现在为止，我们一直在强调，Detour中的算法本质都是2D算法。那么我们在“有高度，有多层”的3D场景中，肯定会有不适应的情况，如下图所示，两点之间在2D中可能直线相连，但是在3D中，极可能出现“空中飞跃”、“穿墙遁地”等不合理情况。

问题分析

分析问题的原因，是因为在2D投影下，我们只需要关心是否可以从当前多边形走向下一个邻居多边形，而不需要关心具体怎么走，因为二者共面。而在3D中，两个多边形在空间中是会有夹角的，此时二者会不共面，那就必须找到两个面的交线，从一个多边形进入到邻居，必须经过这个交线（就是公共边），只有这样，才能保证始终在3D场景的Mesh导航面表面行走。

公共边交点

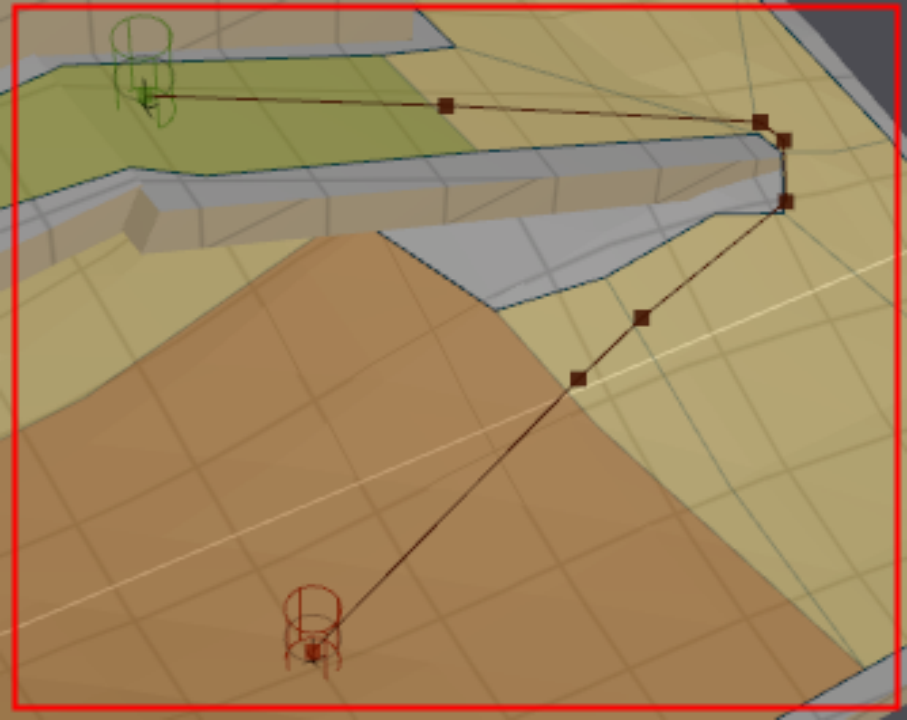
找到了问题的本质，那解决问题的思路也就有了。既然在3D中，从一个多边形进入到另一个多边形需要经过公共边（3D），那么就求解2D投影下的直线路径和路径多边形中所有公共边的交点，需要求解出的是实际3D交点。

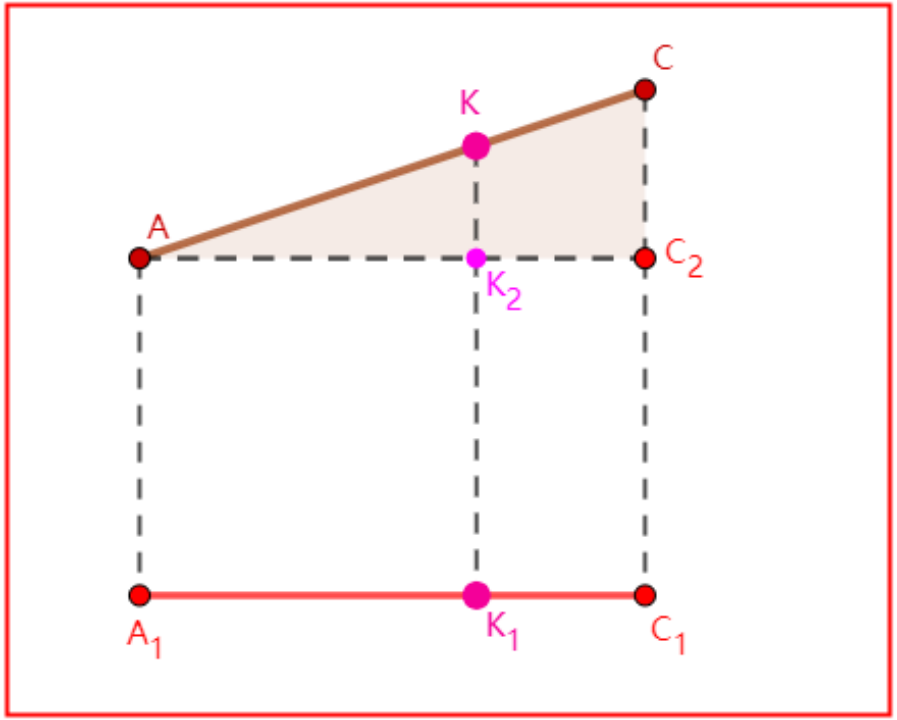
求解交点的3D信息，方法概述（以下图为例）：

首先2D投影的交点不多较少，回顾射线算法中详细介绍的两线段交点的求解。

使用同样的算法可以求解出EK占EF的比例关系。当EF已知的时候，点K的2D坐标就可以得到。（注意理解，此时其实K的高度还拿不到，因为我们要求解的是K在AC上的位置，而不是EF）。

有了K的2D信息，AC已知的情况下，其实就有了K点在AC上的位置关系，比如AK占AC的比例，或者BK占AC的关系。而AC都是有高度信息的，利用该比例关系K在AC上的实际位置就可以得到了。

应用流程

BP3中进行路径平滑之后，会得到很多“拐角点”，而相邻拐角点之间在2D投影上直线相连的。对相连拐角点连线之间的多边形路径进行详细路径点求解，得到每一个路径多边形沿直线进入到下一个多边形在其公共边上的3D交点，以此生成详细路径。