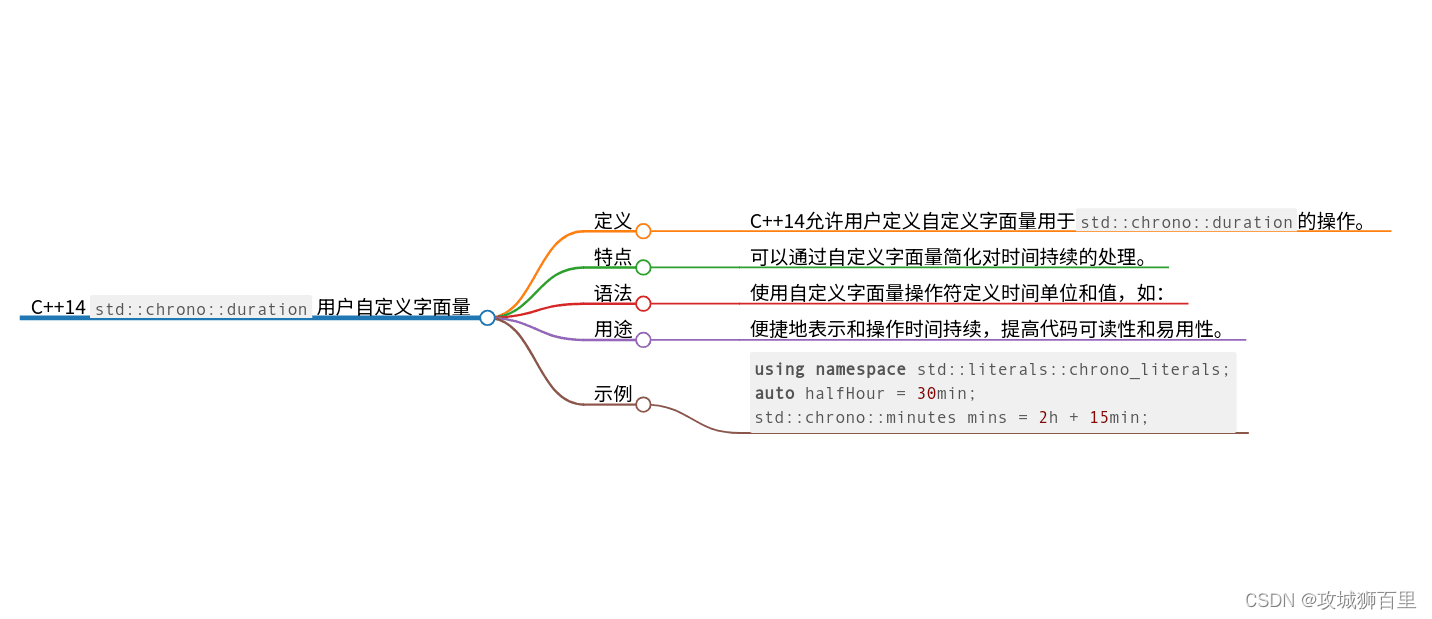
听歌，做题！

1、题目描述

2、逻辑分析

拿到题目一脸懵，有点看不懂啥意思，看了题解才知道啥意思。要实现在常数时间内检索到最小元素的栈，需要使用一个辅助栈来每次存入最小值。

1. 使用Deque作为栈的实现是因为它提供了push、pop和peek等方法，这些方法直接对应栈的基本操作。
2. minStack用于存储当前栈中的最小元素。每次push时，都会比较新元素和minStack的栈顶元素（即当前已知的最小元素），并将较小值push到minStack中。这样，minStack的栈顶元素始终是当前栈中的最小元素。
3. 当执行pop操作时，两个栈都需要同时pop，以确保两个栈的元素是同步的。
4. getMin方法直接返回minStack的栈顶元素，因为该元素始终是当前栈中的最小元素。

3、代码演示

// 使用Deque接口作为栈，因为它提供了push、pop和peek等方法  
    // 主栈，用于存储元素
    Deque<Integer> stack;
    // 辅助栈，用于存储当前栈中的最小元素  
    Deque<Integer> minStack;
    public MinStack() {
         // 使用LinkedList实现Deque接口作为栈
        stack = new LinkedList<Integer>();
        minStack = new LinkedList<Integer>();
        // 初始化minStack时，放入一个Integer的最大值，确保后续push操作时能正确找到新的最小值
        minStack.push(Integer.MAX_VALUE);
    }
    
    public void push(int val) {
        // 在主栈中push元素 
        stack.push(val);
        // 在minStack中push当前元素和minStack栈顶元素中的较小值  
        // 这样minStack的栈顶元素始终是当前栈中的最小元素
        minStack.push(Math.min(val,minStack.peek()));
    }
    
    public void pop() {
        // 从主栈中pop元素
        stack.pop();
        // 同时从minStack中pop元素，因为主栈和minStack的元素是成对push和pop的 
        minStack.pop();
    }
    
    public int top() {
        // 返回主栈的栈顶元素
        return stack.peek();
    }
    
    public int getMin() {
        // 返回minStack的栈顶元素，即当前栈中的最小元素
        return minStack.peek();
    }

4、复杂度分析

• 时间复杂度：对于题目中的所有操作，时间复杂度均为 O(1)。因为栈的插入、删除与读取操作都是O(1)，我们定义的每个操作最多调用栈操作两次。
• 空间复杂度：O(n)，其中 n 为总操作数。最坏情况下，我们会连续插入 n 个元素，此时两个栈占用的空间为 O(n)。