题目来源
-
ABC234G
-
洛谷
Description
给定长度为 n n n 的序列 { a n } \{a_n\} {an}。定义一种将 { a n } \{a_n\} {an} 划分为若干段的方案的价值为每段的最大值减去最小值的差的乘积。求所有划分方案的价值的总和并对 998244353 998244353 998244353 取模。
- 1 ≤ n ≤ 3 × 1 0 5 , 1 ≤ a i ≤ 1 0 9 1\le n\le3\times10^5,1\le a_i\le10^9 1≤n≤3×105,1≤ai≤109。
Solution
由于要求所有划分方案的总和,并且难以存储划分的具体方案,因此我们可以通过动态规划来避免对具体方案进行讨论。
同时,我们可以将求乘积的和转化为将之前求出的和乘上同一个数。
具体而言,若设 f i f_i fi 表示 a 1 ⋯ i a_{1\cdots i} a1⋯i 的划分方案价值之和,则:
f i = ∑ j = 1 i − 1 ( f j × ( max k = j + 1 i { a k } − min k = j + 1 i { a k } ) ) f_i=\sum_{j=1}^{i-1}\Bigg(f_j\times\Big(\max_{k=j+1}^{i}\{a_k\}-\min_{k=j+1}^i\{a_k\}\Big)\Bigg) fi=j=1∑i−1(fj×(k=j+1maxi{ak}−k=j+1mini{ak}))
但这么做效率显然不优,而我们又可以将 max \max max 和 min \min min 分为两个独立的问题进行处理,于是我们应考虑分别计算 Maxsum i = ∑ j = 1 i − 1 ( f j × max k = j + 1 i { a k } ) \text{Maxsum}_i=\sum\limits_{j=1}^{i-1}\Big(f_j\times\max\limits_{k=j+1}^{i}\{a_k\}\Big) Maxsumi=j=1∑i−1(fj×k=j+1maxi{ak}) 以及 Minsum i = ∑ j = 1 i − 1 ( f j × min k = j + 1 i { a k } ) \text{Minsum}_i=\sum\limits_{j=1}^{i-1}\Big(f_j\times\min\limits_{k=j+1}^{i}\{a_k\}\Big) Minsumi=j=1∑i−1(fj×k=j+1mini{ak}),则 f i = Maxsum i − Minsum i f_i=\text{Maxsum}_i-\text{Minsum}_i fi=Maxsumi−Minsumi。
由于 max \max max 和 min \min min 的计算类似,接下来以 max \max max 的相关计算为例。
可以观察到,若将 i i i 从 1 1 1 枚举到 n n n,每次 f j × max k = j + 1 i { a k } f_j\times\max\limits_{k=j+1}^{i}\{a_k\} fj×k=j+1maxi{ak} 的变化是有限的。即 max k = j + 1 i { a k } \max\limits_{k=j+1}^{i}\{a_k\} k=j+1maxi{ak} 只有一段会存在变化,而这一段一定是一个区间 [ x , i ) [x,i) [x,i),其中 x = max t < i , a t > a i t x=\max\limits_{t<i,a_t>a_i}t x=t<i,at>aimaxt,可结合下图理解(只有黑色矩形所在的下标可能成为最大值,且其是最大值的区间在其前一个黑色矩形所在下标到它前一个下标之间,如红色区间所示)。
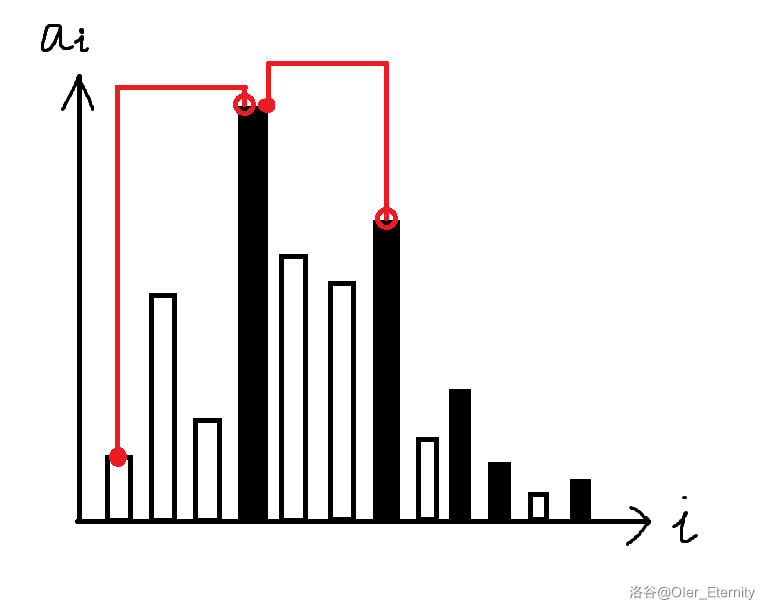
那么我们可以看出来这需要运用到单调栈,栈中储存的是黑色矩形所在下标,用于求出图片上面定义的 x x x 的值。而在同一个红色区间内,最大值不变,只需对 f i f_i fi 进行求和。因此,若设 fsum \text{fsum} fsum 是 f f f 的前缀和函数,我们可以得到 Maxsum i = Maxsum x + ( fsum i − 1 − fsum x − 1 ) × a i \text{Maxsum}_i=\text{Maxsum}_x+(\text{fsum}_{i-1}-\text{fsum}_{x-1})\times a_i Maxsumi=Maxsumx+(fsumi−1−fsumx−1)×ai,那么 max \max max 就可以在 O ( n ) O(n) O(n) 求出, min \min min 同理,单调栈的具体过程可参考代码。
Code
#include <bits/stdc++.h>
using namespace std;
const int p=998244353;
int n,a[300005],Max[300005],top,Maxsum[300005],Min[300005],top2,Minsum[300005],f[300005],fsum[300005];
int main(){
scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
f[0]=fsum[0]=1;
for (int i=1;i<=n;i++){
while (top&&a[i]>=a[Max[top]]) top--;
while (top2&&a[i]<=a[Min[top2]]) top2--;
if (top) Maxsum[i]=(Maxsum[Max[top]]+1ll*(fsum[i-1]-fsum[Max[top]-1]+p)%p*a[i]%p)%p;
else Maxsum[i]=1ll*fsum[i-1]*a[i]%p;
if (top2) Minsum[i]=(Minsum[Min[top2]]+1ll*(fsum[i-1]-fsum[Min[top2]-1]+p)%p*a[i]%p)%p;
else Minsum[i]=1ll*fsum[i-1]*a[i]%p;
f[i]=(Maxsum[i]-Minsum[i]+p)%p,fsum[i]=(fsum[i-1]+f[i])%p;
Max[++top]=i,Min[++top2]=i;
}
printf("%d\n",f[n]);
return 0;
}