基于AOD估计的波束赋形依据压缩感知理论,利用毫米波信道的稀疏特性[18][19],提出对信号的AOA和AOD进行估计,根据估计方向进行波束赋形。由于毫米波信道的稀疏特性,假设有L条多径分量时,公式1中的信道矩阵H可以表示为下式
 (2)
(2)
其中αl表示第l条多径分量幅度响应,aMS(θl)和aBS(φl)分别表示第l条多径分量的接收天线阵列的导向矢量和发送天线阵列的导向矢量。在该算法中,同样也要使用波束训练作为信道估计的依据,其训练过程可以表示为
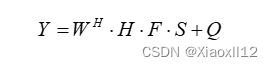 (3)
(3)
其中W和F分别表示接收波束训练矩阵和发送波束训练矩阵,S表示需要发送信号,Y表示训练的后得到的观测结果,Q是训练过程的噪声,上述训练过程可以表示成压缩感知的形式,如下式
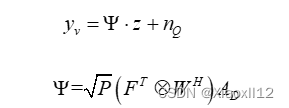 (4)
(4)
(5)
其中Ψ表示测试矩阵,z表示待观测的稀疏向量,为了缩短波束训练的时间复杂度,这里采用多阶训练的方式,其当前时刻的训练矢量由上一时刻的测量结果决定,这与基于码本的波束训练算法大致是一样,其具体过程如图5所示
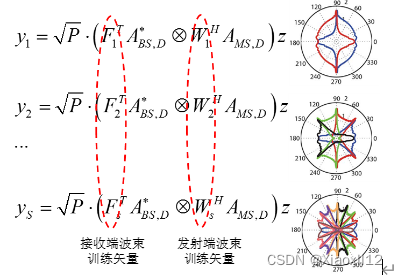
图5. 多阶训练示意图
当信道为单径信道时,该算法步骤为:
- 初始化系统参数,设定N、K、码本F,W;
- 进行第i阶测量,基站端采用码本F(s,ksBS) ,用户端采用码本W(s,ksBS) ,进行K2次测量,得到
- 根据测量结果找到最佳的方向𝑚𝐵𝑆*和𝑚𝑀𝑆*;
- 重复步骤2直到i=S;
在实际的环境中,从发射端到接收端可能存在L条可通信路径,多个路径信号之间可能存在相互干扰,则在波束训练的过程中需要消除路径直接的相互影响,相应的算法步骤为:
- 初始化系统参数,设定N、K、码本F,W;
- 开始估计第l条径的参数,执行单径信道中的第i阶测量,并在测量得到结果中减去已估计的前l-1条径的分量。
- 保留Ld个信号最强的方向,i=i+1,重复步骤2直到i=S。
- 选出一个信号最强的方向,l=l+1,重复步骤2直到l=ld。最后采用LLSE算法估计各路径增益。

图6. 基于CSI的波束赋形(全数字)、基于遍历的波束赋形(模数混合)、基于AOD估计的波束赋形(模数混合)的频谱利用效率仿真对比
图6中给出了基于CSI的波束赋形、基于遍历的波束赋形和基于AOD估计的波束赋形的频谱利用效率的仿真结果,从图中可以看出,当算法训练步数N达到70次时,基于AOD估计的波束赋形的频谱利用效率即可达到基于CSI的波束赋形90%的性能,算法的复杂度相对较低,为毫米波移动通信系统中低复杂度的波束赋形算法的设计提供了理论基础。