归并排序和计数排序

news2024/11/16 7:37:45

1.归并排序

1.1递归

在这里插入图片描述

1.1基本思想

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。
特性：
时间复杂度：O（Nlog N）
空间复杂度:O(N)
归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题

1.2算法描述

把长度为n的序列分为2个亮度为n/2的子序列
对这2个子序列分别采用归并排序
将2个排序好的子序列合成一个最终的排序序列

1.3画图解释

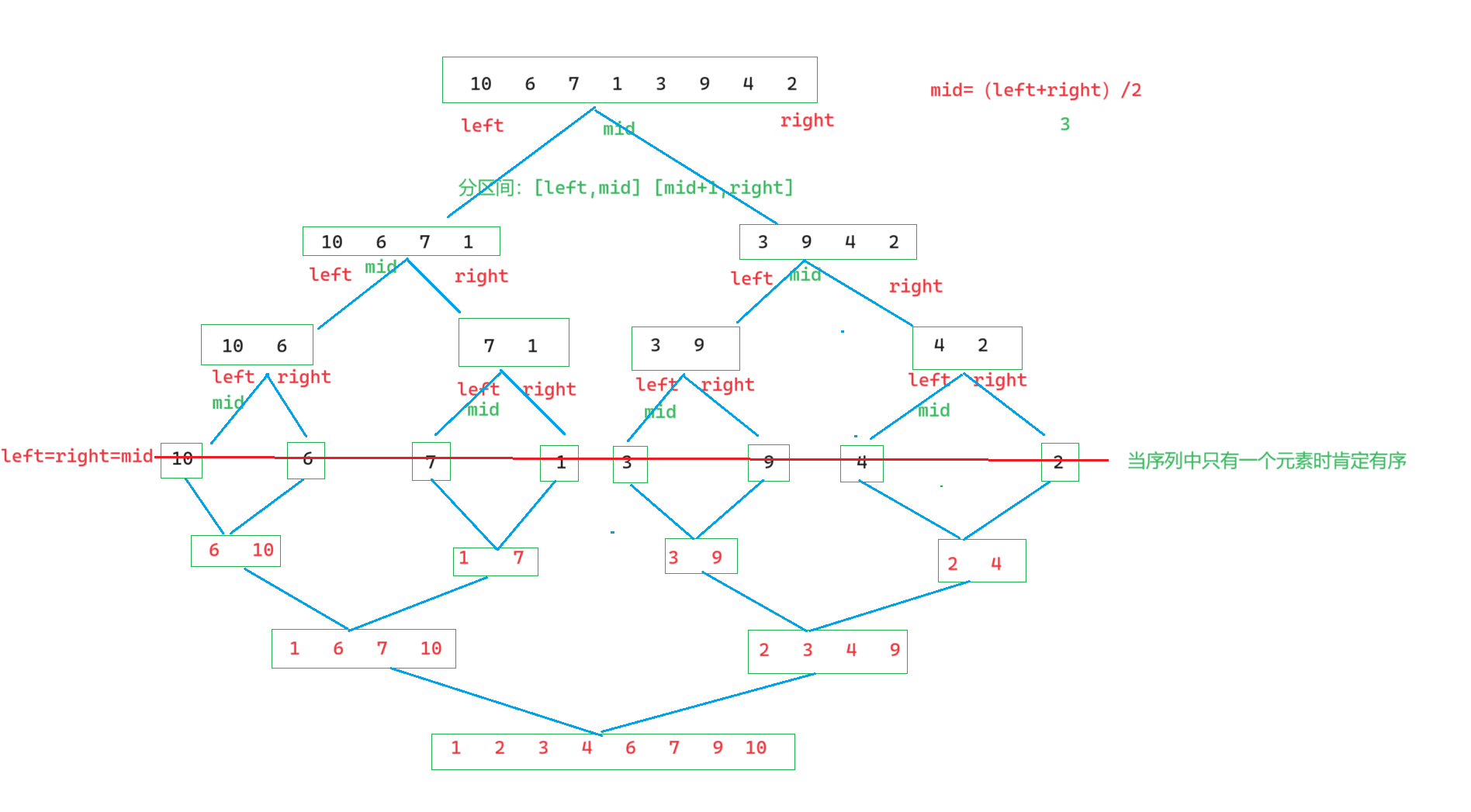
在这里插入图片描述

1.4代码实现

// 归并排序递归实现
void _MergeSort(int* a,int*tmp, int left,int right)
{
	//表示该区间只有一个元素或者该区间不存在
	if (left >= right)
		return;

	int mid = left + ((right - left) >> 1);
	//[left,mid] [mid+1,right]
	//如果有序就进行归并，没有序就继续分治
	_MergeSort(a,tmp, left, mid);
	_MergeSort(a,tmp, mid+1, right);

	//归并
	int begin1 = left;
	int begin2 = mid + 1;
	int i = left;
	while (begin1 <= mid && begin2 <= right)
	{
		//两子序列比较大小
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	//两子序列其中一个序列走完了
	//1.假设第1个子序列走完了，将第2个子序列放入tmp数组中
	//2.假设第2个子序列走完了，将第1个子序列放入tmp数组中
	while (begin1 <= mid)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= right)
	{
		tmp[i++] = a[begin2++];
	}
	//放入tmp数组完成
	
	//将tmp数组的数copy到a数组中
	memcpy(a+left, tmp+left, (right - left + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
	//申请空间
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	//申请空间成功
	_MergeSort(a, tmp, 0, n - 1);

	free(tmp);
	tmp = NULL;
}

1.2非递归

先11归并，再22归并，再44归并…以2的倍数进行归并

// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i+ gap - 1;
			int begin2 = i + gap, end2 =i + 2 * gap - 1;
			int j = begin1;
			//如果第二组越界，第二组就不用归并了
			if (begin2 >= n)
			{
				break;
			}
			//如果第二组只一部分越界，就修改第二组的范围
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			while (begin1 <= end1 && begin2 <= end2)
			{
				//两子序列比较大小
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			//两子序列其中一个序列走完了
			//1.假设第1个子序列走完了，将第2个子序列放入tmp数组中
			//2.假设第2个子序列走完了，将第1个子序列放入tmp数组中
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			//将tmp数组中元素copy到a数组中
			memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));
		}
		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}

2.计数排序

在这里插入图片描述

2.1基本思想

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
特性：

计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
时间复杂度：O(MAX(N,范围))
空间复杂度:O(范围)

2.2算法描述

找出待排序的数组中最大和最小的元素；
统计数组中每一个值为i的元素出现的次数，存入新数组的第i项；
对所有的计数累加；
反向填充目标数组：将每个元素i放在新数组的第i项，每放一个元素就-1.

3.画图解释

在这里插入图片描述

// 计数排序
void CountSort(int* a, int n)
{
	//找最大，最小值
	int max =a[0];
	int min =a[0];
	for (int i = 1; i < n; i++)
	{
		if (max < a[i])
			max = a[i];
		if (min > a[i])
			min = a[i];
	}
	//申请空间
	// 计数
	int* count = (int*)malloc(sizeof(int) * (max - min + 1));
	memset(count, 0, sizeof(int)*(max-min+1));
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}
	//排序
	int range = (max - min + 1);
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}