• 标题：Offline RL Without Off-Policy Evaluation
• 文章链接：Offline RL Without Off-Policy Evaluation
• 代码：davidbrandfonbrener/onestep-rl
• 发表：NIPS 2021
• 领域：离线强化学习（offline/batch RL）—— RL-Based / One-step

---

• 摘要：先前的大多数 Offline-RL 方法都采用了涉及 Off-policy evaluation 的迭代 Actor-Critic (AC) 方法。本文中我们证明了只需简单地基于 behavior policy 的 on-policy $Q$ 价值估计做一步 constrained/regularized policy improvement，就会表现得惊人地好。这种 One-step 算法在大部分 D4RL benchmark 上击败了之前的迭代算法。这种 One-step baseline 在实现强大性能的同时，比以前提出的迭代算法简单很多，且对超参数更鲁棒。我们认为，迭代方法之所以性能较差，一方面是因为执行 Off-policy evaluation 时固有的高方差导致价值估计不准，另一方面是因为基于这些低质量价值估计迭代进行 policy improvement 会放大价值估计问题。此外，我们认为 One-step 算法的强大性能是由于它结合了 “环境中的有利结构” 和 “行为策略”

1. 背景

1.1 Offline RL

• Offline RL 是这样一种问题设定：Learner 可以获取由一批 episodes 或 transitions 构成的固定交互数据集，要求 Learner 直接利用它训练得到一个好的策略，而且禁止 Learner 和环境进行任何交互，示意图如下
  
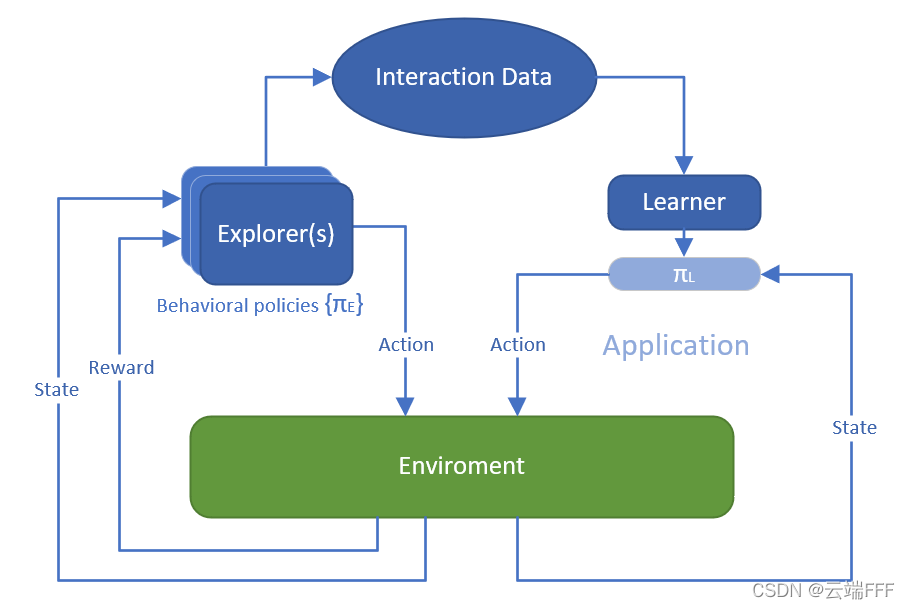
  关于 Offline RL 的详细介绍，请参考 Offline/Batch RL简介
• Offline RL 是近年来很火的一个方向，下图显示了 2019 年以来该领域的重要工作
  
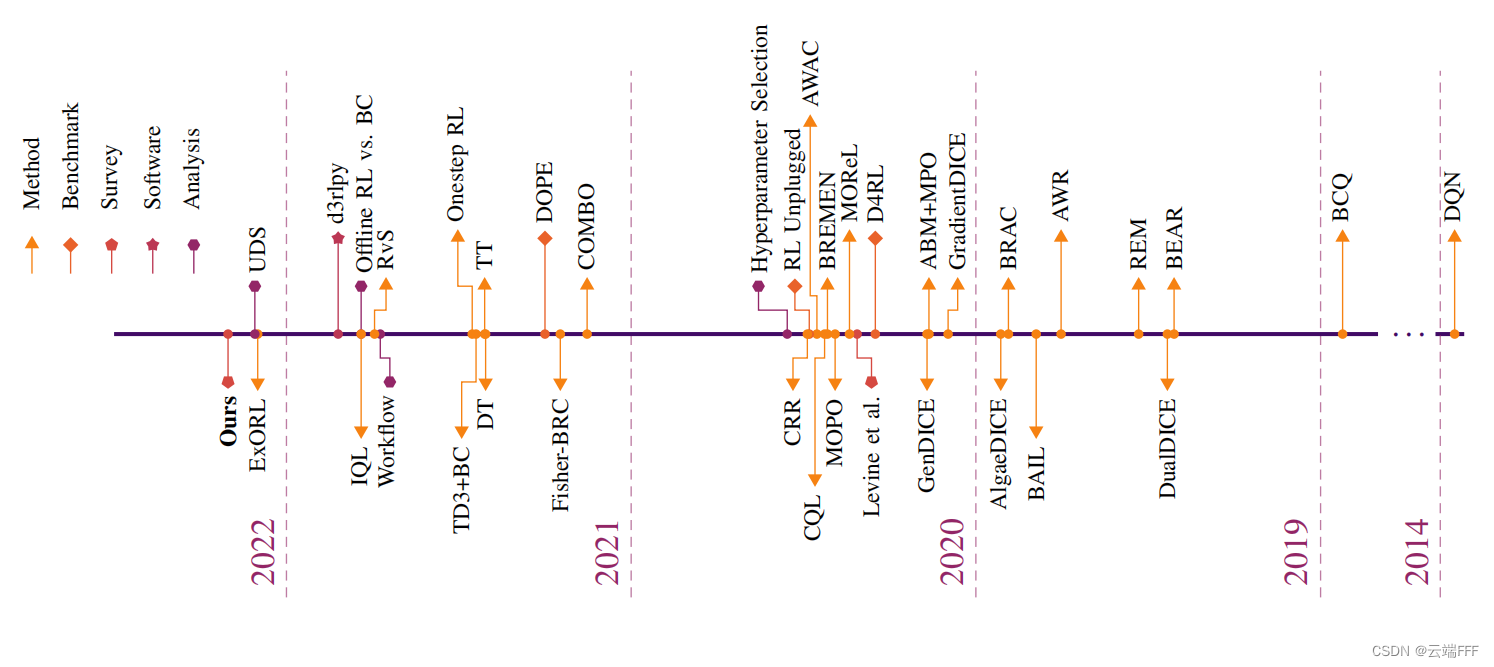
  本文出现在 21 年，严格地讲作者其实没有提出新方法，只是发现了 “Offline 设定下，One-step 这种 train schedule，作为广义策略迭代（GPI）的一个特例，可以取得高性能” 这一现象，并深入探究分析了其原因，揭示了 Offline RL 训练的一些规律和特点，有较强的启发性
• 本文给出的 Offline RL Preliminaries 如下

  考虑有限 MDP M = { S , A , ρ , P , R , γ } \mathcal{M}=\{\mathcal{S,A},\rho,P,R,\gamma\} M={S,A,ρ,P,R,γ}，离线数据集 $D_N$ 由某 behavior policy $\beta$ 收集的 $(s_i,a_i,r_i)$ 组成，期望奖励为 $r(s,a)={\mathbb{E}}_{r|s,a}[r]$，任意策略 $\pi$ 的 $Q$ 价值定义为
  $$Q^{\pi }(s,a):={\mathbb{E}}_{P,\pi \mid s_0=s,a_0=a}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r\left(s_t,a_t\right)\right]$$ 目标是最大化学得策略的期望 return
  $$J(\pi ):=\underset{\rho ,P,\pi }{\mathbb{E}}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r\left(s_t,a_t\right)\right]=\underset{\begin{array}{c}s\sim \rho \\ a\sim \pi \mid s\end{array}}{\mathbb{E}}\left[Q^{\pi }(s,a)\right]$$ 允许访问环境来调优一组少量的（< 10）超参数集

1.2 One-step & Multi-step

• 解释一下 One-step 概念，这是针对要做 policy evaluation 价值评估的 RL-based 类 Offline RL 方法而言的。大多数这类方法都是基于 Bellman 等式做 TD-Learning 来评估价值的，整个过程服从广义策略迭代（GPI）框架，即迭代进行 policy evaluation 和 policy improvement 两步，其中

  1. policy evaluation 阶段：先用上一步迭代的价值估计 ${\hat{Q}}^{{\pi }_{k-2}}$ 进行 warm-start，然后用数据集 $Q_N$ 估计当前策略 ${\pi }_{k-1}$ 的价值 ${\hat{Q}}^{{\pi }_{k-1}}$
  2. policy improvement 阶段：先用上一步迭代的最新策略 ${\pi }_{k-1}$ 进行 warm-start，然后根据估计价值 ${\hat{Q}}^{{\pi }_{k-1}}$、估计的行为策略 $\beta$ 和数据集 $D_N$ 来更新得到策略 ${\pi }_k$

  归纳得到如下通用算法模板
  
  根据 GPI 迭代的次数和程度，作者区分了以下几个概念

  1. One-step：迭代次数 $K=1$。首先通过最大似然（比如 MC）得到 behavior policy 的估计 $\hat{\beta }$，然后做 Policy evaluation 至价值收敛，得到 behavior policy 的价值估计 ${\hat{Q}}^{\beta }$，最后做一步 Policy improvement 得到 ${\pi }_1$ 就结束。注意这个过程完全避免了 off-policy 的 bootstrap 计算
  2. Multi-step：迭代次数 $K>1$，其他都和 One-step 一样，注意每一次 Policy evaluation 都要评估至收敛。由于 Offline 数据集是由 behavior policy $\beta$ 收集的，对 ${\pi }_k,k\ge 2$ 进行的 Policy evaluation 一定都是 Off-policy 的
  3. Iterative actor-critic：这个很类似 Multi-step，区别在于使用更大的超参数 $K$，且不要求每次迭代中的 Policy evaluation 收敛。通常这里 evaluation 和 improvement 两步都使用梯度方法，具体使用的 operators 可以和 Multi-step 中相同

• 下图（来自 R_BVE 论文）展示了 One-step 和其他两种涉及 Off-policy evaluation 的 Iterative 方法在流程上的区别
  
  下图（来自本文）显示了策略空间上的区别，注意学得策略 ${\pi }_i$ 被约束在 behavior policy $\beta$ 附近的安全范围内
  

1.3 Related work

• Iterative 方法：这类方法涉及到 $Q$ 函数的多步 iterative & off-policy 评估，涵盖了上文提到的 Multi-step 和 Iterative actor-critic，过去大多数 RL-based 类算法都属此类。为了减轻 Extrapolation Error（见 BCQ 论文解析 2.1 节） 问题对价值估计质量的影响，这些方法提出各种措施来确保学得策略不会偏离 behavior policy 太远，大致可以分成以下三类
  1. policy constraints/regularization： 直接优化 policy，使之和 behavior policy 接近。一类做法是对策略网络施加强约束，使其只选择 “能使 $(s,a)$ 具有足够数据集支撑” 的动作 $a$（比如在 BC 的基础上加一个随机扰动），代表方法有 BCQ、SPIBB 等；另一类做法是在策略网络的优化目标中增加 KL、MMD 等正则化项，鼓励学得策略和 behavior policy 接近，代表方法有 BEAR 等
  2. modifications of imitation learning：基本都是 BC 的变体，比如先过滤掉低 $Q$ 价值数据再做模仿学习，或者根据 $Q$ 价值进行加权模仿。代表方法有 ABM、BAIL、COIL 等
  3. Q regularization：这类方法主要从 $Q$ 函数估计（或者说 critic 的优化目标）入手，通过引入正则化措施，对未知或不确定的 $(s,a)$ 保持悲观态度，从而间接地鼓励学得策略呆在 behavior policy 附近。比如 BRAC、CQL、Fisher-BRC、R_BVE 等
• one-step 方法：这类方法只对 behavior policy 做一次 on-policy 的 $Q$ 价值评估，然后优化一步 policy 结束，不涉及任何 iterative & off-policy 评估操作，不存在 Extrapolation Error 问题。过去的方法有
  1. 在 D4RL 上做连续控制的 YOEO，该方法比较复杂，涉及 distributional $Q$ 函数及其 ensembles，以及一种新正则化器，本文考虑的设定在能取得相似性能的情况下更简单，且更侧重分析
  2. 针对 Atari 等离散问题的 R_BVE，这种情况下 policy improvement 可以基于 $Q$ 估计精确地进行，本文则主要针对连续控制问题；另外 R_BVE 将 Iterative 方法的问题归结于对 $Q$ 价值的高估，本文则进一步探讨了导致高估的原因
• 其实理解 One-step 的做法之后，熟悉 RL 的读者应该对它的性能有一个大概的估计了，One-step 只对 behavior policy 做了一步提升，其实不会比 behavior policy 好太多，特别是 behavior policy 比较差的时候，One-step 学到的策略 ${\pi }_1$ 应该也是挺差的。但人们发现很多时候 One-step 的性能常比 Multi-step 和 Iterative actor-critic 等 Off-policy 迭代方法强很多，这就说明一定有一些因素破坏了多步方法的性能，本文对此现象进行进一步分析，贡献包括
  1. 提出了一个简单的 one-step baseline，其在很多 Offline RL 问题上优于更复杂的 Iterative 方法
  2. 检查了 Iterative 方法中 off-policy 价值评估的失效模式
  3. 描述了何时 one-step 算法可能优于 Iterative 方法

2. 本文方法

• 先回顾一下前面的算法模板
  
  • 对于 policy improvement，作者考察了以下常用算子
    1. Behavior cloning：直接返回 $\hat{\beta }$ 作为新的策略 $\pi$，其它算子应至少超过这个最简单的 baseline。这个算子和上文的 “modifications of imitation learning” 相关
    2. Constrained policy updates：BCQ 和 SPIBB 等算法使用这类算子将 policy 限制在 behavior policy 附近，作者这里用了一个简化版本的 BCQ 算子，称之 easy BCQ，它去掉了扰动网络，改成从 $\hat{\beta }$ 中采样 $M$ 个样本，然后根据 ${\hat{Q}}^{\beta }$ 贪心地更新策略，如下
       $${\hat{\pi }}_k^M(a\mid s)=1\left[a=\arg \underset{a_j}{\max }\left\{{\hat{Q}}^{{\pi }_{k-1}}\left(s,a_j\right):a_j\sim {\pi }_{k-1}(\cdot \mid s),1\le j\le M\right\}\right]$$ 这个算子和上文的 “policy constraints/regularization” 相关

       Note：这里我感觉公式有点问题，策略的优化过程没有被约束到 behavior policy 附加，候选动作 $a_j$ 应当采样自 $\hat{\beta }$，即改成
       $${\hat{\pi }}_k^M(a\mid s)=1\left[a=\arg \underset{a_j}{\max }\left\{{\hat{Q}}^{{\pi }_{k-1}}\left(s,a_j\right):a_j\sim \hat{\beta },1\le j\le M\right\}\right]$$

    3. Regularized policy updates：BRAC 等算法使用这类算子向 Offline RL 的最大化 return 目标中引入正则项，来控制策略优化过程中和 behavior policy 的偏离程度。给定任意散度 $D$，如下进行 policy improvement
       $${\hat{\pi }}_k^{\alpha }=\arg \underset{\pi }{\max }\sum _i\underset{a\sim \pi \mid s}{\mathbb{E}}\left[{\hat{Q}}^{{\pi }_{k-1}}\left(s_i,a\right)\right]-\alpha D\left(\hat{\beta }\left(\cdot \mid s_i\right),\pi \left(\cdot \mid s_i\right)\right)$$ 过去的研究发现 $D$ 的不同选择影响不大，实践中通常使用 reverse KL divergence $KL(\pi (\cdot |s_i)||\hat{\beta }(\cdot |s_i))$。直观上看，这种正则化迫使 $\pi$ 保持在 $\beta$ 的支持下，而 2 中的正则化鼓励 $\pi$ 覆盖 $\beta$。此算子和上文的 “Q regularization” 相关
    4. Variants of imitation learning：这类算子通过对观察到的行为进行过滤或加权来修改模仿学习算法，以进行 policy improvement。作者这里使用优势估计的指数来加权动作
       $${\hat{\pi }}_k^{\tau }=\arg \underset{\pi }{\max }\sum _i\exp \left(\tau \left({\hat{Q}}^{{\pi }_{k-1}}\left(s_i,a_i\right)-\hat{V}\left(s_i\right)\right)\right)\log \pi \left(a_i\mid s_i\right)$$ 这个算子和上文的 “modifications of imitation learning” 相关
  • 对于 policy evaluation，本文作者仅考虑了 DDPG 那种简单的配合 target 网络进行的 td-style learning，没有使用更复杂的 Double Q Learning 或 Q ensembles 等做法，作者认为这些值得未来进一步研究

3. 实验

• 作者将 one-step、multi-step、iterative 等算法模板和 Easy BCQ、reverse KL regularization、exponentially weighted imitation 等 improvement operator 进行各种组合，并在 D4RL 数据集上测试性能
  
  这里第一列是 D4RL 里几种 Iterative 算法经过超参数调优后的最佳结果，后面是使用不同 policy improvement 算子的 one-step 方法。可见大多数情况下 one-step 都超过了 Iterative 方法，唯一的例外是在 random 数据集上
• 为了进一步探索 one-step 的性能特点，作者对使用 Rev KL Reg 算子的 one-step 方法进行了更多迭代，性能如下
  
  发现更多的迭代计算往往破坏性能，这启发我们：在尝试一些更复杂的东西之前，将 one-step 算法作为 baseline 运行是值得的，这种简单的方法经常取得更好的性能

4. 讨论

4.1 迭代算法的问题

4.1.1 问题的表现

• 作者通过调整 Rev KL Reg 算子中逆 KL 散度正则化项的系数来调整约束强度，考察不同强度下的训练曲线
  
  可见
  1. Iterative & multi-step 方法的训练过程在约束强度不足时会迅速崩溃，加强正则化可以帮助防止这种崩溃，因为对行为策略的足够强的正则化确保了评估几乎是 on-policy 的
  2. one-step 方法关于约束强度要鲁棒得多，且其最优约束强度也要低一些
  3. 当约束足够强时，各种方法的性能差不多，这是因为学得策略被严格约束到 behavior policy 附近，policy evaluation 过程几乎变成和 one-step 一样的 on-policy 了
• 作者将迭代算法崩溃的原因归咎于 Distribution shift 和 Iterative error exploitation，下面分别说明

4.1.2 Distribution shift

• 这个老生常谈了，任何依赖于 off-policy evaluation 的算法都会遇到 Distribution shift 问题，这会减少有效样本量，并增加估计的方差。过去有一些文章对此进行了理论分析，BCQ 论文中将这个问题称作 Extrapolation Error，为了减轻此问题，大多数 RL-based 方法都要对 policy 施加约束，这也产生了这类方法的一个核心矛盾：为了得到并利用更准确的价值估计，学得策略不能离 behavior policy 太远，而我们又想学得策略性能尽量超越 behavior policy，因此二者又不能离得太近，需要估计并利用那些 OOD 的 $(s,a)$ 对应的价值，这里就产生了一个 trade-off
• 作者检查了 off-policy 评估过程中 Distribution shift 发生的过程。先用 behavior policy 采样一个数据集从头训练 $Q$ 价值，然后从 reply buffer 中采样 1000 个数据检查 $Q$ 估计质量
  
  可见约束越弱，Distribution shift 问题越严重，$Q$ 估计质量越低；而约束足够强时，off-policy 评估的 $Q$ 估计质量又和 on-policy 差不多了

4.1.3 Iterative error exploitation

• Iterative & multi-step 方法在 policy evaluation 时会使用上一轮迭代的价值估计进行 warm-start，并使用和 policy improvement 步骤相同的数据，这导致了步骤间的依赖性，并引发 Iterative error exploitation 问题。简而言之，产生该问题的原因是 policy improvement 步骤中 ${\pi }_i$ 倾向于选择 overestimate 的动作（这些动作通常是 OOD 的），然后这种高估会由于重用数据而在 policy evaluation 步骤中通过动态规划传播，R_BVE 论文中对此问题有清晰的解释
  
  另一张相当直观的示意图如下
  
• 作者也做了一点理论分析，考虑在每个 $(s,a)$ 处，基于行为策略 $\beta$ 收集的固定数据集，对当前策略 $\pi$ 进行policy evaluation 时会有 ${\epsilon }_{\beta }^{\pi }(s,a)$ 的误差，即价值估计为
  $$\begin{gathered} {\hat{Q}}^{\pi }(s,a)=r(s,a)+\gamma \underset{\begin{array}{c}{s}^{\prime }|s,a \\ {a}^{\prime }\sim \pi |s^{\prime }\end{array}}{\mathbb{E}}\left[{\hat{Q}}^{\pi }\left(s^{\prime },a^{\prime }\right)\right]+{\epsilon }_{\beta }^{\pi }(s,a). \end{gathered}$$ 这里误差 ${\epsilon }_{\beta }^{\pi }(s,a)$ 吸收了包括 函数近似误差 和 缺乏样本导致的误差 等所有误差，它通常随着数据集覆盖程度减小而增大。只要 ${\epsilon }_{\beta }^{\pi }(s,a)$ 在在不同的 $\pi$ 之间高度相关就会导致 Iterative error exploitation，为了简单起见，这里假设 ${\epsilon }_{\beta }^{\pi }(s,a)$ 对于使用固定数据集评估的所有策略 $\pi$ 都是相同的，并把符号简化为 ${\epsilon }_{\beta }$，这种情况下估计误差不依赖于被评估的策略 $\pi$，因而可以将其看作辅助 reward，即有
  $${\hat{Q}}^{\pi }(s,a)=Q^{\pi }(s,a)+{\tilde{Q}}_{\beta }^{\pi }(s,a),{\tilde{Q}}_{\beta }^{\pi }(s,a):=\underset{\pi \mid s_0,a_0=s,a}{\mathbb{E}}\left[\sum _{t=0}^{\infty }{\gamma }^t{\epsilon }_{\beta }\left(s_t,a_t\right)\right]$$ 这样一来，当使用上一步的 $\hat{Q}$ 构造 TD target 进行 warm-start 时，误差 ${\epsilon }_{\beta }$ 就会自然地传播。下面我们可以概括一下 Iterative error exploitation 的过程：
  1. 给定固定数据集，就会决定一个随着距离数据集支撑范围而增大的 “辅助奖励” ${\epsilon }_{\beta }$
  2. 在不加约束的情况下，迭代算法会不断增大这个 “辅助奖励”，导致当前学得策略 ${\pi }_i$ 越来越远离行为策略 $\beta$，使得 ${\tilde{Q}}_{\beta }^{{\pi }_i}(s,a)$ 相对 $Q^{{\pi }_i}(s,a)$ 变得更大
  3. 尽管随着迭代进行，$Q^{{\pi }_i}(s,a)$ 可能给出比 $Q^{\beta }(s,a)$ 更好的信号，但它很容易被 ${\tilde{Q}}_{\beta }^{{\pi }_i}(s,a)$ 淹没
  4. 相比而言，${\tilde{Q}}_{\beta }^{\beta }(s,a)$ 的幅度更小，因此 one-step 算法对误差更有鲁棒性
• 作者同时给出了例子说明
  
  这个网格环境有一个确定性奖励为 1 的好状态和一系列奖励分布为 $N(-0.5,1)$ 的坏状态，因为所有的误差都来自缺乏样本导致的奖励估计错误，所以 ${\epsilon }_{\beta }$ 确实在所有的 $\pi$ 上都是恒定的。直观地说，当有这么多的噪声状态时，很可能其中的一些会被高估，由于重用数据，这些高估持续存在并在状态空间中传播，产生 Iterative error exploitation，实验也表明这时 one-step 确实常优于 Iterative 方法。在 benchmark 中的许多高维控制问题中，这种 “具有许多估计不佳的状态” 的特性很可能也存在，特别是当 Offline 数据分布狭窄时更是如此
• 另外作者发现，如果打破迭代过程中由于 “重用数据” 和 “用上轮 $Q$ 估计进行 warm-start” 而引入的依赖性，Iterative error exploitation 问题可以缓解
  
  这里右图中每次 policy evaluation 都是重新独立采样数据，从头开始进行的，可见价值高估得到有效缓解，不过这不影响 4.2 节中的 Distribution shift 问题

4.2 迭代方法的优势

• 根据上一节的讨论，我们知道 multi-step 和 iterative 方法会传播估计误差 ${\tilde{Q}}_{\beta }^{{\pi }_i}(s,a)$，但不应忽视它们在传播噪声的同时也传播了有用的信号 $Q^{{\pi }_i}(s,a)$，如果数据集有足够的覆盖范围来降低噪声的大小，信号的传播相对来说就不容易被误差 ${\tilde{Q}}_{\beta }^{{\pi }_i}(s,a)$ 淹没，这可以帮助迭代算法的训练。如下示例
  
  这里仅仅将 behavior policy 改成了更倾向于走向带噪声状态，使得 Offline 数据能充分覆盖这些状态，就能有效降低价值估计的误差，使多步 Iterative 方法能进行可靠的，更积极的规划；另一方面由于降低了 behavior policy 进入右上角良好状态的概率，损害了 one-step 方法的奖励信号传播，这两个变化使得 Iterative 方法的性能显著优于 one-step
• 另一个更加直观的实验如下
  
  如图可见这里将来自 random behavior policy 的数据与来自 medium behavior policy 的数据按不同比例进行混合来构造 Offline 数据集，可见只需引入一点 medium 数据，就能破坏 Iterative 方法使之不如 one-step 的性能了