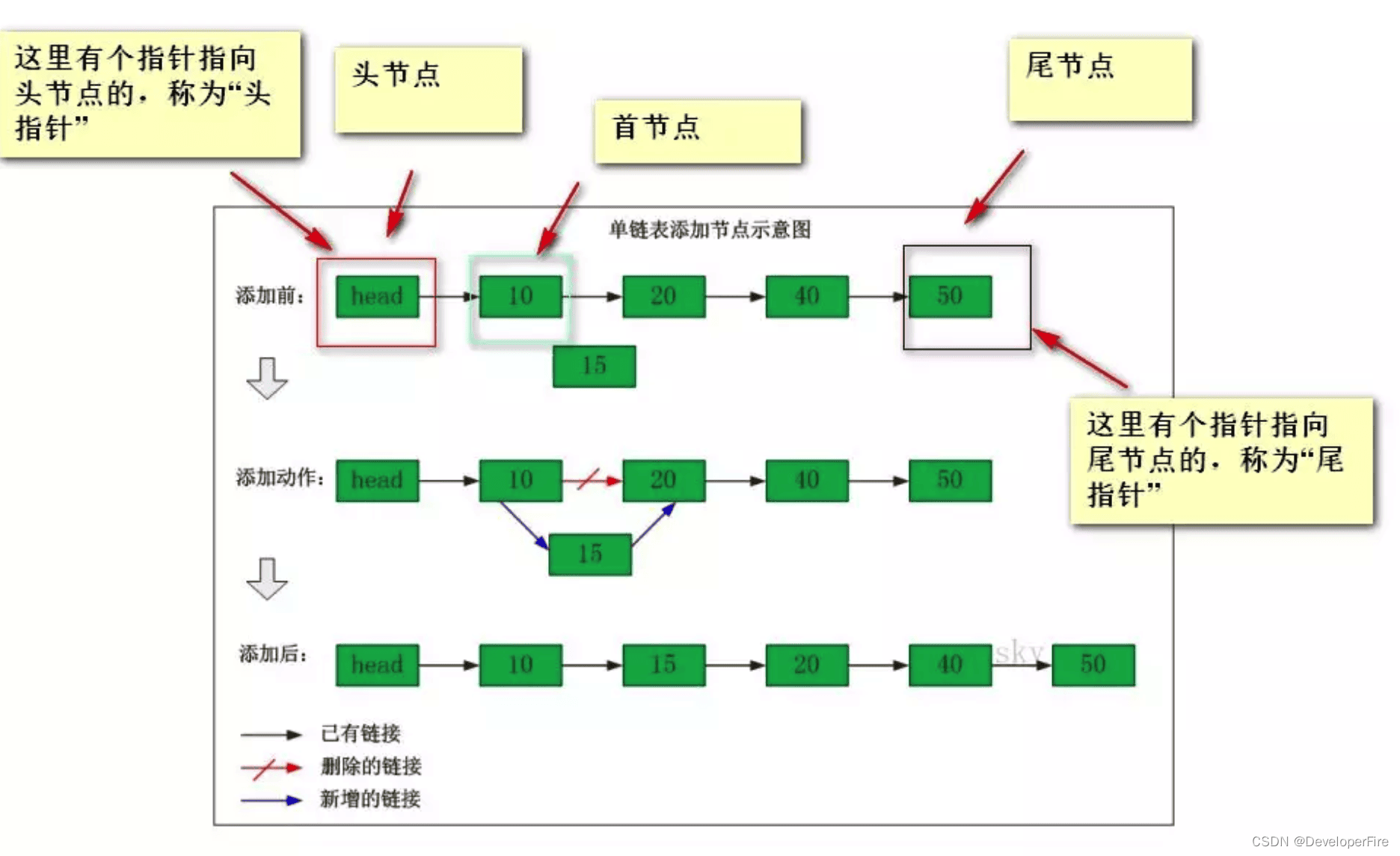
AES算法原理

1. 对称加密算法（用于取代DES算法，发展历史DES-3DES-AES）

2. 明文长度固定为128位（DES：64位），密钥长度可128位、192位、256位（DES：64位）

加密原理

最终轮没有列混合运算！

字节顺序

因为AES明文加密每组为128bit，16byte = 128bit，它的排列方式为如下（字节为单位）：

1. 初始变化

将每组的明文128bit和密钥的128bit进行异或得到一轮初始变换

2. 9轮循环运算

2.1 字节代还

通过上面得到了一个和子密钥异或完的64byte(128bit)数据，然后将每个字节看作一个x，y坐标，到S-BOX表中进行索引值，并填入原来的位置，如图：

最终替换完成表的数据为如下图：

2.2 行移位

同样将数据分为16个字节，以字节为单位进行行移位，第一行不变，第二行向左移动1byte，第三行向左移动2byte，第四行向左移动3byte。例子步骤如图所示：

2.3 列混合

将拿到的16个字节矩阵进行左乘一个固定的4*4的矩阵（相乘算法看下面列混合相乘章节）。例子步骤如图所示：

比如:第一行：(02,03,01,01) * (d4,bf,5d,30) = (02 * d4) xor (03 * bf) xor 5d xor 30 = 04

第二行：(01,02,03,01) * (e0,b4,52,ae) = e0 xor (02 * b4) xor (03 * 52) xor ae = cb

第三行：(01,01,02,03) * (b8,41,11,f1) = d3

第三行：(03,01,01,02) * (1e,27,98,e5) = 4c

补充：(01,02,03,01) * (e0,b4,52,ae) = 66

2.4 轮密钥加

将列混合后的数据与经过轮密钥后的子密钥（子密钥由来看下面密钥加密章节）进行列对列异或，得到新的数据

3. 最终轮

在经过前面的9轮步骤后，第十次加密时，不采用列混合步骤其他步骤一样，完成最终的明文加密到密文

密钥加密

当密钥为16byte时（128bit）先将该数据进行列分类，例子如图所示：其中i的取值分为2种情况，如下图思维图所示，其中T()表示一个轮函数

字循环：将1个字（Word）中4个字节（byte）循环左移1个字节，即[b[0],b[1],b[2],b[3]] -> [b[1],b[2],b[3],b[0]]

字节代换：对字循环的结果使用S盒进行字节代换，S盒如下图1所示

轮常量异或：将字节代换的结果用轮常量Rco[j]进行异或，j表示轮数，轮常量表如图2：

​ 图一：S盒

​ 图二：轮常量表

那么T(W[3]) 可计算为[09,cf,4f,3c] -----> [cf,4f,3c,09] ------> [8a,84,eb,01] -------> [8b,84,eb,01]

设i = 4，这里i是4的倍数表示为W[4] = W[0] xor T(W[3]) 其中T由字循环、字节代换、轮常量异或组成。

则W[4] = [2b,7e,15,16] xor [8b,84,eb,01] = [a0,fa,fe,17]

设i = 5，那么不是4的倍数则表示为W[5] = W[1] xor W[4]

则W[5] = [28,ae,d2,a6] xor [a0,fa,fe,17] = [88,54,2c,b1]

最后经过10轮加密后的密钥为如图所示：每一轮的密钥对应每一轮的明文加密（比如我在第一轮加密就使用Round key 1依此类推）

列混合相乘

在一个数(记为a)与2相乘时:

​ 先转换为二进制->(00000010) * (a7 a6 a5 a4 a3 a2 a1 a0) 当a7为0时算术左移一位-> (a7 a6 a5 a4 a3 a2 a1 a0 0) ，当a7不为0时 (a7 a6 a5 a4 a3 a2 a1 a0 0) xor (00011011)

在一个数(记为a)与3相乘时:

​ 先转换为二进制->(00000011) * (a7 a6 a5 a4 a3 a2 a1 a0) = (00000010 xor 00000001) * (a7 a6 a5 a4 a3 a2 a1 a0) = (00000010 * (a7 a6 a5 a4 a3 a2 a1 a0)) xor (a7 a6 a5 a4 a3 a2 a1 a0) ####可理解为a乘以2再加上一个a

在一个数(记为a)与4相乘时:

​ 先转换为二进制->(00000100) * (a7 a6 a5 a4 a3 a2 a1 a0) = 00000010* 00000010 * (a7 a6 a5 a4 a3 a2 a1 a0)

例题1：求 2 * 0xd4
= 00000010 * 11010100 #这里的a7为1
= 10101000 xor 00011011 #那么就是0xd4算术左移一位，取异或值
= 10110011
例题2: 求 3 * 0xbf
= (00000011 * 10111111)
= (00000010 * 10111111) xor 10111111  #这里的a7为1
= (01111110 xor 00011011 ) xor 10111111 
= 11011010

例题3: (02 * b4) xor (03 * 52)
= (00000010 * 10110100) xor (00000011 * 01010010)
= (01101000 xor 00011011) xor ((00000010 * 01010010) xor 01010010)
= (01101000 xor 00011011) xor (10100100 xor 01010010)
= 10000101

byte x=0x3,byte y=0x63 求x*y
= (00000011 * 01100011)
= (00000010 * 01100011) xor  01100011
= 11000110 xor 01100011
= 0xa5