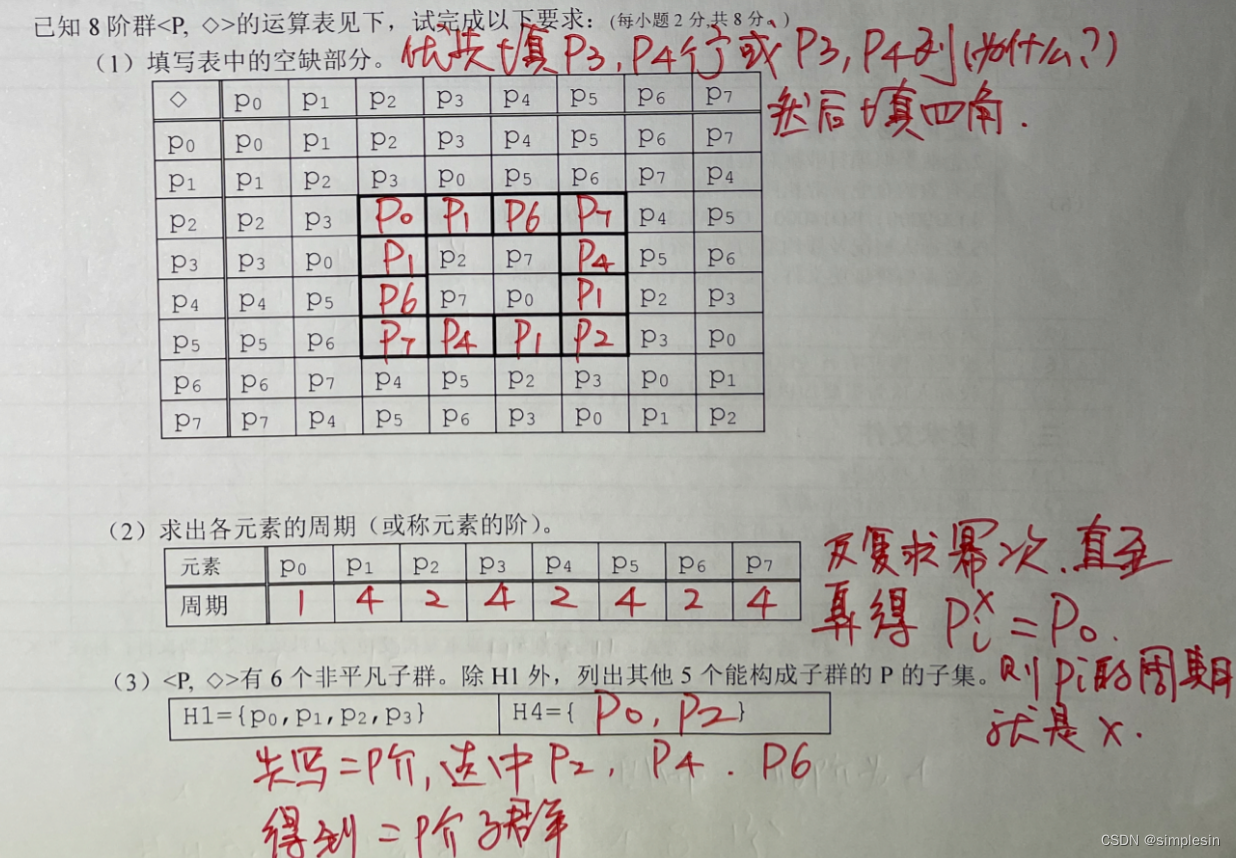






1.先找到e,这里是0
2.对每个元素求它的阶
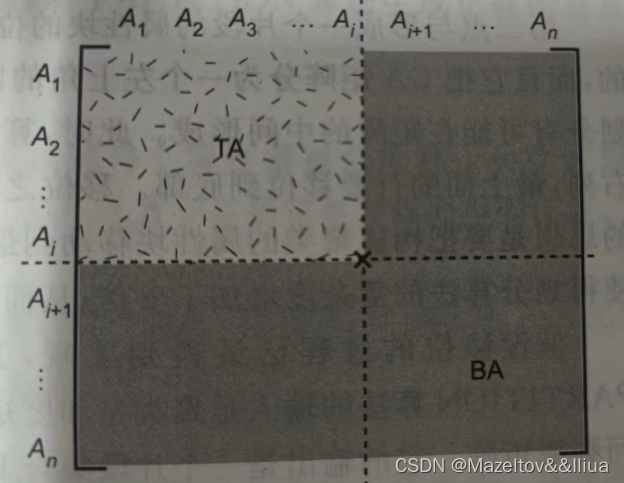
3.根据拉格朗日定理,子群的阶必须是群 G 的阶的因数。群 G 的阶为 10,它的因数有 1、2、5 和 10。这意味着子群的阶可能是 1、2、5 或者 10。
4.相同阶的就放为一组,也就是它的一个子群

而且,因为它没有klein四元群,因为二阶的只有5,0。只有两个元素,无法构成Klein四元群。
 一个12阶循环群可以表示为 \(G=\langle a \rangle\),其中 \(a\) 是群的一个生成元,且 \(a^{12}=e\)(\(e\) 代表单位元)。要找这个群的所有子群,可以根据拉格朗日定理,子群的阶必须是12的因数。12的正因数有1, 2, 3, 4, 6, 12。
一个12阶循环群可以表示为 \(G=\langle a \rangle\),其中 \(a\) 是群的一个生成元,且 \(a^{12}=e\)(\(e\) 代表单位元)。要找这个群的所有子群,可以根据拉格朗日定理,子群的阶必须是12的因数。12的正因数有1, 2, 3, 4, 6, 12。
对于每个可能的阶数,可以这样构造子群:
1. **阶数为1的子群**:始终是包含单位元 \(e\) 的平凡子群 \(\{e\}\)。
2. **阶数为2的子群**:需要找到群元素的一个平方等于单位元的。在 \(G=\langle a \rangle\) 中,\(a^6=a^{12/2}\) 的阶为2,因此子群为 \(\{e, a^6\}\)。
3. **阶数为3的子群**:需要找到群元素的一个三次方等于单位元的。在 \(G\) 中,\(a^4=a^{12/3}\) 的阶为3,因此子群为 \(\{e, a^4, a^8\}\)。
4. **阶数为4的子群**:需要找到群元素的一个四次方等于单位元的。在 \(G\) 中,\(a^3=a^{12/4}\) 的阶为4,因此子群为 \(\{e, a^3, a^6, a^9\}\)。
5. **阶数为6的子群**:需要找到群元素的一个六次方等于单位元的。子群为 \(\{e, a^2, a^4, a^6, a^8, a^{10}\}\)。
6. **阶数为12的子群**:整个群本身 \(\{e, a, a^2, a^3, a^4, a^5, a^6, a^7, a^8, a^9, a^{10}, a^{11}\}\)。
因此,12阶循环群有6个不同的子群,这些子群也是循环的,并且可以通过群的生成元以及上述规则确定。
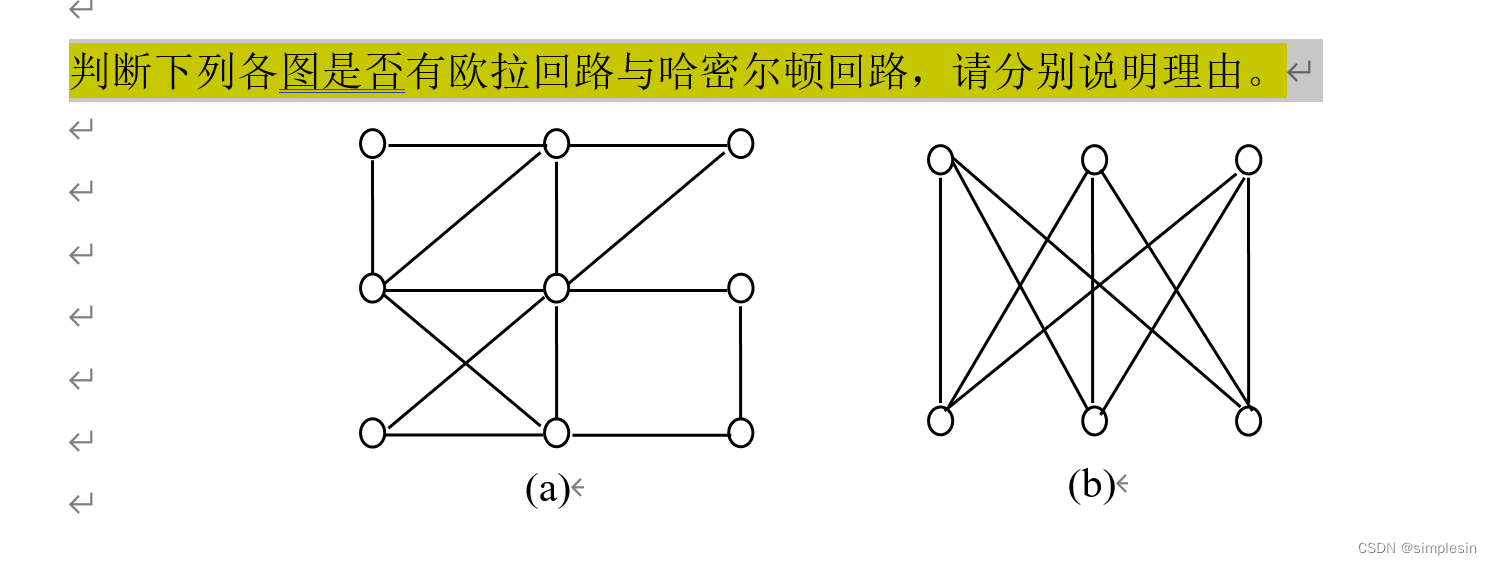
判断是否是欧拉回路:每个顶点是否是偶数度
判断是否是哈密尔顿回路:直觉+如果不是,搬出连通分支大于删除顶点的个数这个定理