在复习分布式数据库这一部分时，发现垂直分片较难理解，上网上查找资料，也发现找不到，固在考试结束后将自己的理解记录下来。
垂直分片的计算总体上分为三个步骤;1、属性亲和度矩阵AA的计算；2、聚类亲和度CA矩阵的计算；3、进行划分。
话不多说，我们开始以例题为例，进行引入

对于上述例子，给出了查询集合Q ，属性集合A，和站点集合S。

一、AA矩阵计算：
首先我们需要知道对于每个查询q,共访问的频次。对于查询q1来说，其访问的频次为站点S1的访问频次+站点S2的访问频次+站点S3的访问频次=30。同理，我们可以知晓对于查询q2,q3,q4,q5的访问频次，用矩阵的形式表示为[q1,q2,q3,q4,q5] = [30,15,40,10,15]

之后，我们定义属性亲和度AA，结果如下。这个亲和度矩阵的原理是这样的;
我们先来看图a，在a中关注数值不为0的，对于查询q1来说，数值不为0的属性为A2，A3，A5，这三个进行两两组合,可得到的组合为（A2，A3）、（A2，A5）、（A3，A5）然后再相应的AA矩阵中对应的位置填上q1的频次。即，（A2，A3）对应的位置为30：这里注意，每个组合会填上两次，因为矩阵是对角的。
同理，对于q2来说，不为0的位置为A1,A2，A3，A5,那么所得的组合为（A1，A2）（A1，A3）（A1，A5）（A2，A3）（A2，A5）（A3，A5），同样在其对应的位置填上q2的频次，如果原位置有数值，直接相加即可。
对于每个查询q，都执行上述的步骤，即可得到下面的AA矩阵

上述的这种方式，计算的相对来说较慢，因为相同的还要相加。有另一种方式，比较容易快的得到。比如：在查询q1中，我们得到了一下组合：（A2，A3）、（A2，A5）、（A3，A5），对于组合（A2，A3）中，我们在图a中观察，哪个查询同时在A2和A3中有数值：可以看到是查询q1、q2、q5：所以（A2，A3）处的值应该为q1+q2+q5 = 30+15+15 = 60，可以直接的得到。同理对于（A2，A5）来说，查询q1、q2 ,所以对应的数值为30+15 = 45，因此，这种方式可以很快速的得到AA矩阵。

下面对于对角线上的值进行计算。对角线（A1，A1）的值即为所有访问A1属性的查询加和。所以（A1，A1）上的值应该为 = q2+q3+q5 = 15+40+15 = 70，同理可计算其他对角线的值。

二、聚类亲和度矩阵CA的计算
CA的计算主要可以分为以下几步：
（1）初始化：从AA中任选一列，将其放入到CA中，一般选择第一列
（2）迭代。逐一选取剩余的n-i列（i是已经放入CA的列的数目）的每一列，尝试把他们放入到CA所剩余的i+1个位置上，所选择的位置应当对前面所描述的全局亲和度度量贡献最大，继续这一步骤，直到没有在可以放置的列
（3）行排序：一旦列的顺序决定，行的放置也应当改变，使得他们的相对位置和列的相对位置匹配
以AA矩阵为基础，初始化：在AA矩阵上随机选择一列（一般选择第1列）作为CA矩阵的第一列，之后，将第两列插入到CA中，初始时，我们默认有一个0列（其数据全部为0），则第二列无论插入第一列的左边还是右边都是一样的。（这个之后我们计算cont的时候可以知晓），但是一般第二列是会插入到第一列右边的。
之后将第三列插入到1,2列的位置。那么有以下三种插入方法：0-3-1，和1-3-2
cont(A0,A3,A1) = 2(bond(A0,A3)+bond(A3,A1)-bond(A0,A1)) = 2(0+3070+6030+3070+5545) = 16950
cont(A1,A3,A2) = 2(bond(A1,A3)+bond(A3,A2)-bond(A1,A2)) = 22050
所以选择将A3插入到A1和A2中间 。
同理，在将A4插入到A1，A2，A3时，其可以插入到A1的左边、右边。A2的右边等位置。同理我们可以计算A5.注意在插入时，插入到哪两个中间，则计算这三者的cont
最终得到的CA矩阵为：

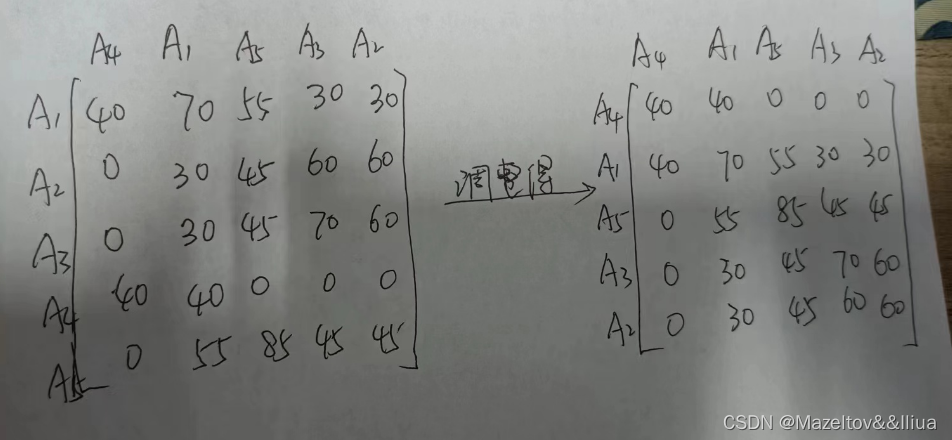
最后需要调整CA矩阵的行，使其和列相同 ，形成一个对角矩阵

三，划分
划分主要是在CA矩阵的基础上，以对角线进行划分属性。如下图的这种形式所示

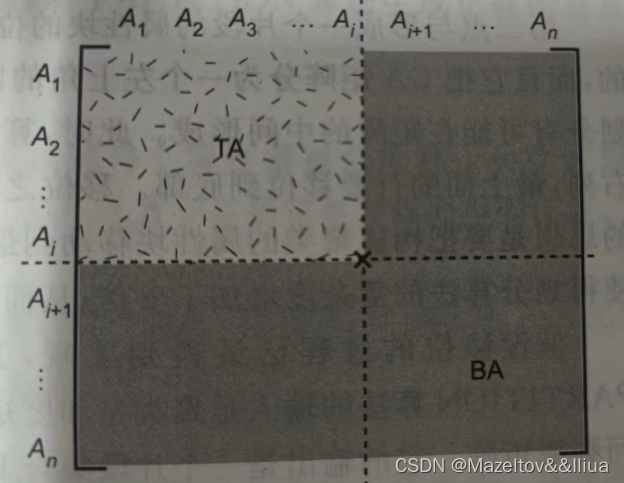
以CA矩阵为基础，
当n=1时，TA = {A4}，BA = {A1，A2，A3，A5}
TQ为空，BQ={q1,q2,q4,q5},OQ= {q3},其中TQ是查询中仅仅只访问TA的，BQ是查询中仅仅访问BA的，OQ是查询中既访问TA集合又访问BA集合的。
同理当n=2时，TA = {A4，A1}，BA = {A2，A3，A5}
TQ为空，BQ={q1,q4},OQ= {q2，q3，q5}
当n=3时，TA = {A4，A1，A5}，BA = {A2，A3}
TQ为{q3}，BQ={q4},OQ= {q1，q2，q5}
当n=4时，TA = {A4，A1，A5，A3}，BA = {A2}
TQ为{q3，q4}，BQ为空,OQ= {q1，q2，q5}
Z = CTQCBQ -COQ2，其中CTQ为ref（qk）的值乘以TQ集合的所有查询的频次相加
根据这个公式，我们可以计算相应的
Z1 = 10*（30+15+10+15）-40的平方 =-1600，这是因为TQ为空
同理可以计算Z2 = -4900，Z3=-3200，Z4=-3600
所以划分点n=1出，由于主键是A1，所以属性的划分为：
F={R1，R2}
R1= {A1，A4}
R2={A1，A2，A3，A5}

至此，垂直分片属性划分已完成