简介

在机器人学和控制理论中，雅可比矩阵扮演着至关重要的角色。它是一个描述机器人末端执行器速度与关节速度之间关系的数学工具。通过雅可比矩阵，我们可以更好地理解和控制机器人的运动，特别是在执行精确操作时。雅可比矩阵的计算通常基于机器人的运动学模型。对于串联机器人，雅可比矩阵可以通过微分运动学方程来计算。这涉及到对机器人的正向运动学方程进行微分，以找到关节速度与末端执行器速度之间的关系。

在机器人学和控制理论的领域内，雅可比矩阵（Jacobian matrix）构成了理解和操控机器人动力学行为的核心数学框架。该矩阵精确地阐述了机器人末端执行器的速率向量与其关节速率向量之间的线性映射关系，从而为机器人的精确控制与路径规划提供了理论基础。雅可比矩阵的构建与求解过程，通常依赖于机器人的运动学模型，尤其是对于串联连杆型机器人（serial manipulators），其雅可比矩阵的推导涉及对正向运动学方程的微分运算，旨在揭示关节空间的速率变化如何影响任务空间中末端执行器的速率变化。

在形式化表述中，雅可比矩阵定义为末端执行器速度向量(${\mathbf{v}}_{\text{ee}}$)关于关节速度向量($\mathbf{q}$）的偏导数矩阵，即：

$$J(\mathbf{q})=\frac{\partial {\mathbf{v}}_{\text{ee}}}{\partial \mathbf{q}}$$

其中，$J(\mathbf{q})\in {\mathbb{R}}^{m\times n}$ 是雅可比矩阵，$m$表示末端执行器的自由度，$n$ 表示机器人的关节数目，而${\mathbf{v}}_{\text{ee}}$ 和 $\mathbf{q}$ 分别表示末端执行器的速度和关节的位移。

雅可比矩阵的计算过程涉及对机器人的运动学方程进行微分，这一过程需要考虑到机器人的几何结构、关节配置以及连杆间的相对运动。在实际操作中，雅可比矩阵的求解通常通过数值方法或解析方法实现，其中解析方法因其计算效率和精度而在实际工程应用中更为常见。

雅可比矩阵不仅在机器人的动力学建模和控制中发挥着关键作用，而且在机器人的逆运动学求解、路径规划、碰撞检测以及传感器融合等多个领域中都有着广泛的应用。通过深入研究雅可比矩阵的性质，如其秩、条件数和奇异性，可以为机器人系统的稳定性分析和性能优化提供重要的理论依据。因此，雅可比矩阵是连接机器人关节空间与任务空间的桥梁，是实现高精度机器人控制不可或缺的工具。

求解方法

较为常用的有速度雅可比矩阵、力雅可比矩阵，其中，力雅可比矩阵是速度雅可比矩阵的转置，可表示为：

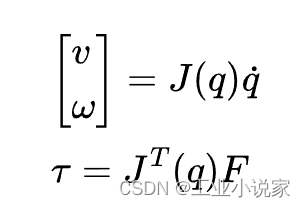
公式中，$v$ 和 $\omega$ 是笛卡尔空间（工作空间）中的速度和角速度，并且 $\dot q $是一个关节速度向量。

对于一般的串联机器人在构造雅可比矩阵时，主要有三种方法：

1. 矢量积分法：是一种建立在运动坐标系概念基础上的雅可比矩阵构造方法。
2. 指数积分法：是一种基于机器人运动方程的指数积分公式推导的方法。
3. 微分变换法：即根据机器人末端坐标系或基坐标系得微小平移和旋转运动导致得末端位姿变化，将这种变化等价变换，即可构造出机器人的雅可比矩阵。

根据微分变换的等价变换，可得出(详细推算可见[1])：

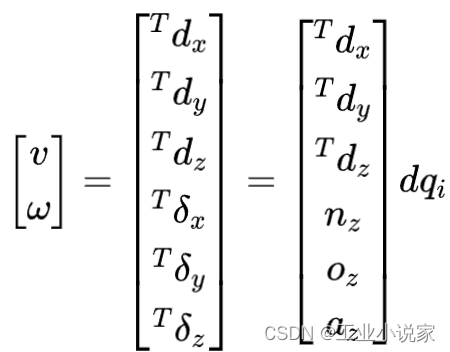
其中，$n、o、a$矢量构成第i连杆坐标系到机器人末端坐标系之间变换的，其形式为：

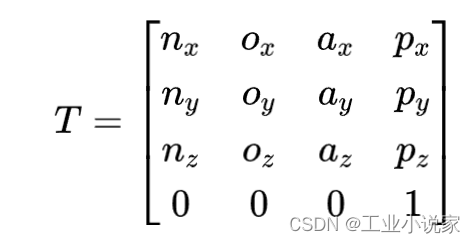
对于转动关节的第i个连杆，其雅可比矩阵的列矢量为：

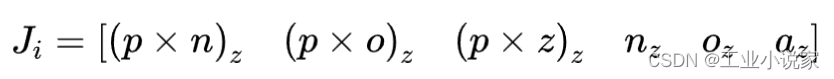
对于平移关节的第i个连杆，其雅可比矩阵的列矢量为：

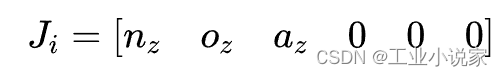
利用上述方法得到的雅可比矩阵列矢量，代表了关节坐标矢量的一个分量的微分运动量与机器人末端坐标系的广义位置矢量的微分运动量之间的关系。因此，通过上述两式求取旋转关节和平移关节到机器人末端的雅可比矩阵列矢量时，需要首先求取该关节到机器人末端的变换矩阵。

对于第6个关节，也就是该关节的连杆坐标系到末端坐标系的变换矩阵。由于是转动关节，根据下式：

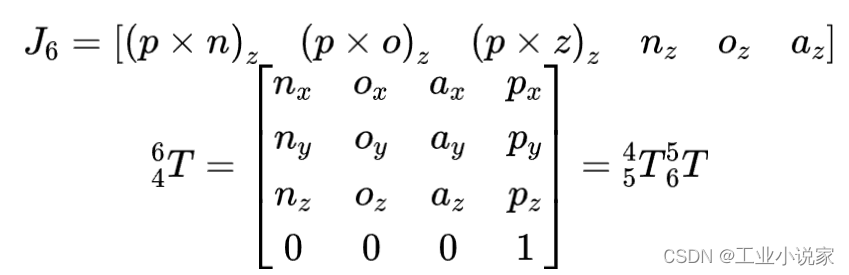
${}_5^{4}T{}_6^{5}T$ 为已知变量，根据上上式即可求解出$J_6$。以此类推即可求解出所有的$J_i$.

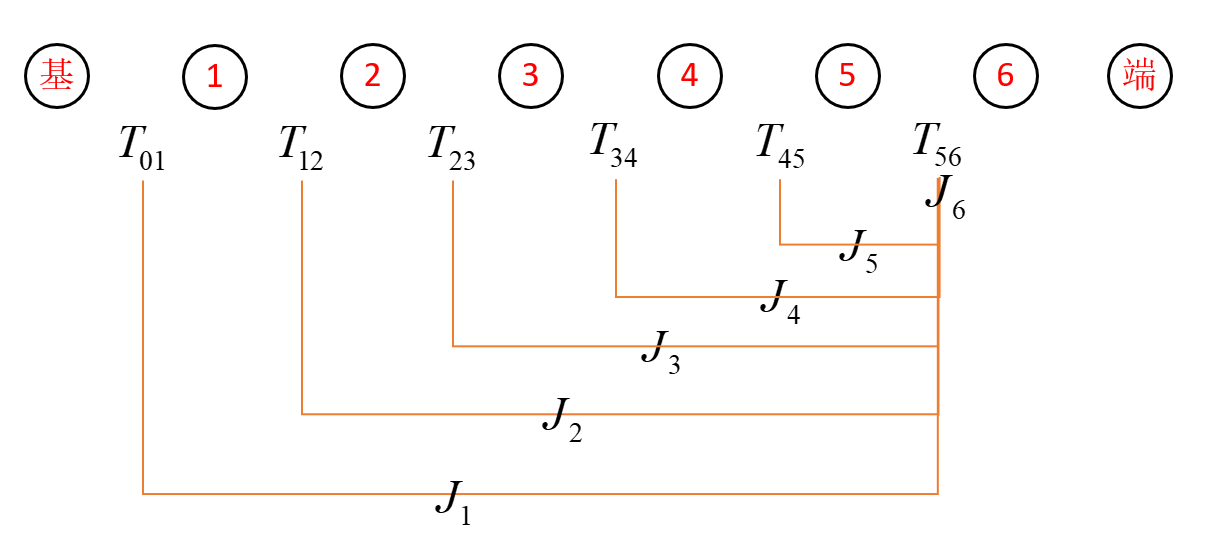
最后，即可写出该机器人的雅可比矩阵为：

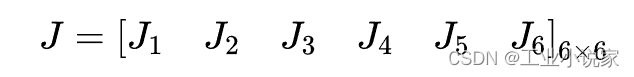
MATLAB机器人工具箱求解

利用MATLAB机器人工具箱，可进行如下编写，其中UR5机器人模型程序编写请见：

clear,clc,close all;
%% 建立机器人DH参数，初始状态为竖直状态
L1=Link('d',162.50,'a',0,'alpha',0,'modified');
L2=Link('d',0,'a',0,'alpha',pi/2,'offset',pi/2,'modified');
L3=Link('d',0,'a',425,'alpha',0,'modified');
L4=Link('d',126.70+6.6,'a',392.25,'alpha',0,'offset',pi/2,'modified');
L5=Link('d',99.70,'a',0,'alpha',pi/2,'modified');
L6=Link('d',99.60-4.5,'a',0,'alpha',-pi/2,'modified');
 
robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','UR5')

% 假设六自由度的串联机器人的各个关节的角度如下：
qn = [0 0.7854 3.1416 0 0.7854 0];

%jacob0()求解的是将关节速度映射到世界坐标系中的末端执行器空间速度
robot.jacob0(qn)
%jaconb()求解的是将关节速度映射到工具坐标系中的末端执行器空间速度
robot.jacobe(qn)

可得：

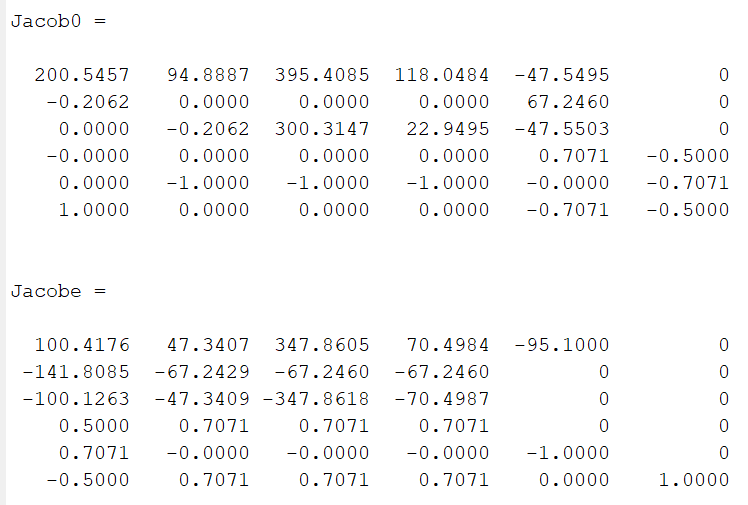
奇异性

即：奇异位形，指在机器人的工作空间中，其末端参考点不能实现沿任意方向的微小位移或转动时相应机器人的位形。为机器人的一个重要的运动学特性。

从机器人运动学来说，我们在已知线性变换可以将关节速度和笛卡尔速度联系起来，但大多数机器人的线性变换矩阵都会出现不可逆现象，在变换矩阵出现不可逆时，其对应的机器人位形即奇异位形，简称奇异性。

造成后果： 当机械手运动到奇异位置时,产生的不良影响主要表现在三个方面:
使机器人的实际操作自由度减少，从而手部无法实现沿着某些方向的运动，同时减少了独立的内部关节变量数目。
某些关节角速度趋向无穷大,引起机器人失控,导致执行器偏离了规定的轨道。
使雅可比矩阵退化,从而所有包括雅可比的求逆控制方案无法实现。

分类： 通常分为两类：

1. 边界奇异位形：机器人在完全展开或者收回使得末端执行器处于或非常接近工作空间边界的情况；
2. 内部奇异位形：是远离工作空间时，通常是由于两个或多个关节轴线共线引起的。

参考文献

[1]谭民.先进机器人控制[M].高等教育出版社,2007.

往期推荐