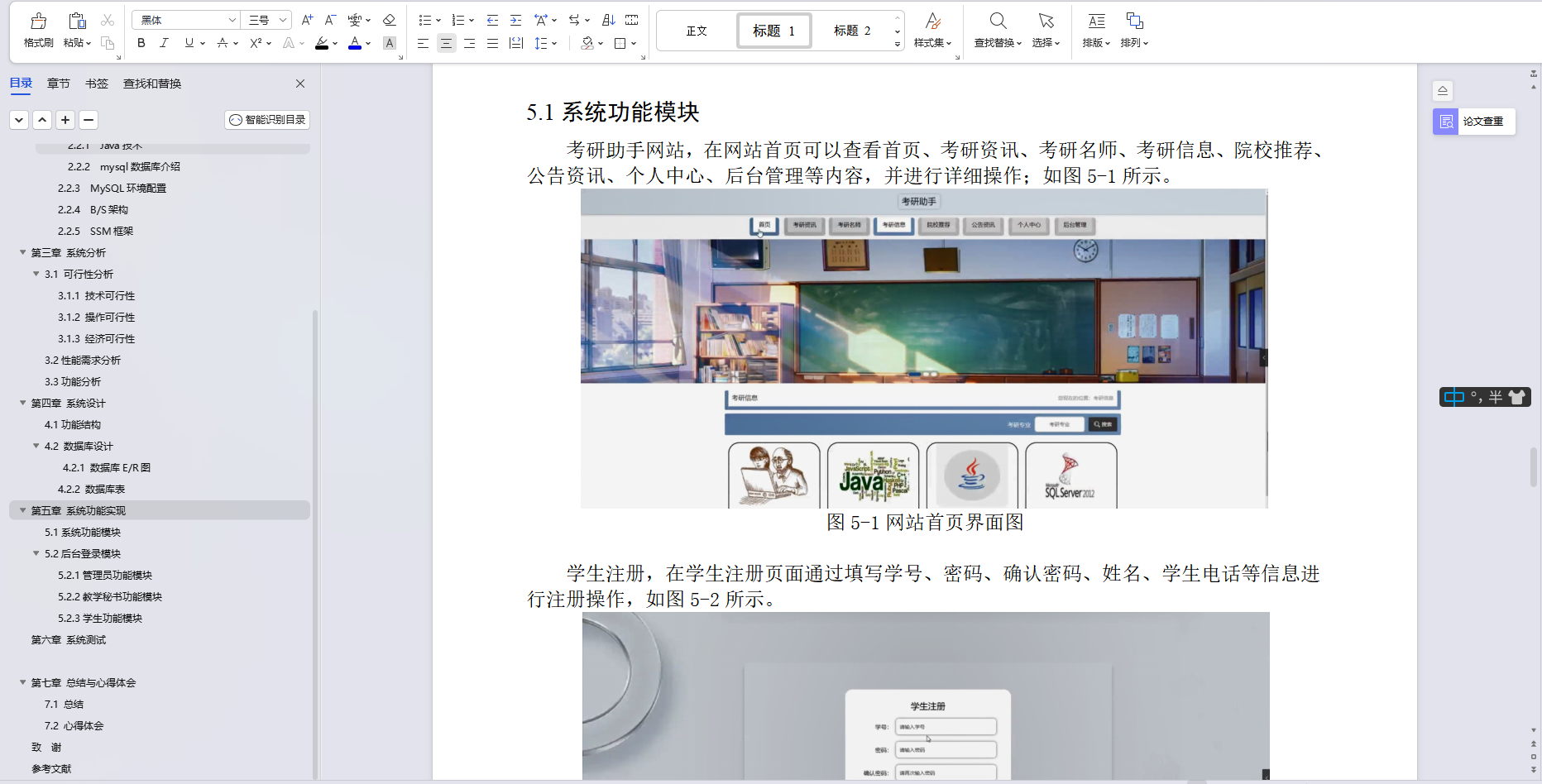
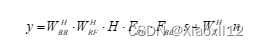模板匹配算法：基于模板相关性匹配的手写数字识别

news2024/11/18 0:26:55

1 前言

得益于硬件技术的发展，基于深度学习的各种识别方法如火如荼，在各种应用场景中都取得很好的效果。本人入行深度学习领域若干年，做过很多项目的工程化评估，对于神经网络是如何工作的也解释不清楚，只是知道这样做是可行的。有的时候，给客户介绍说，做某目标识别算法，如果采用深度学习的方法可以做到多高多高的性能，客户有时候会反问道：那么相比于传统方法，深度学习有多少性能提高？我通常无法直接回答这个问题，虽然我知道深度学习的方法肯定会比传统方法更好，但是我没有做相应的实验，没有对比，没有证据。我只好说，神经网络是黑盒模型，虽然不知道底层逻辑是如何运作的，但是有理论证明神经网络可以拟合任意函数，所以神经网络要比传统方法更强大。客户似懂未懂地点点头，不再说话，我知道他对这个回答并不满意。对于他这种级别的人物，掌握着项目的命运，对具体的技术细节不关心，只关心最终的效果。后来给另一个客户做算法性能评估，我使用神经网络算法进行性能评估，最后性能并不理想，精度只有80%左右，我跟客户说，神经网络模型在这种类型的信号识别精度不是很高，客户说，没关系，只要证明神经网络算法比传统方法好就行了，然后让我做证明去了。经过一些列事情之后，我在终于开始重视起来传统的方法来。

2 理论基础

在没有神经网络之前，人们是如何实现图片的分类和识别的呢？比如说，一个陌生人，你从来没见过他，但是给你一张他的照片，你能否从茫茫人海中认出他来？我想，只要你不是脸盲的话，你是有很大概率能认出来的。当然，能不能认出来，辨认的难度如何，还跟照片和本人的匹配程度有关。如果给我一张照片，让我从一群人中去找出照片中的人，我会拿出照片一个一个地去比对，然后给匹配程度打分，最后选出得分最高的人，那个人就是照片中的人。这种方法就是模板匹配，匹配程度就是相关性。用作模板的就是那张照片，被用来比对的人就是样本，那么相关性是什么，我们通常用相关系数来评估相关性。下面以手写数字识别为例，介绍模板相关匹配算法。

手写数字识别是各种人工智能算法教程的入门级别例子。手写数字有一个数据集，叫MNIST数据集，该数据集有60000张训练样本，有10000张测试样本，包含0-9一共10个手写体数字图片，图片的大小为28*28像素，如下图所示。

这里使用的模板匹配算法，是基于图片的相关性。在概率论中，相关系数是通过无量纲化协方差描述的：

$\rho _{XY}=\frac{cov(X,Y)}{\sigma _{X}\sigma _{Y}}$

设(X,Y)是二维随机变量，两个分量的方差都存在，则称 $\rho _{XY}$ 为X与Y的相关系数，其中 $\sigma _{X}=\sqrt{D(X)}$

$\sigma _{Y}=\sqrt{D(Y)}$

$cov(X,Y)=E\left \{ \left [ X-E(X) \right ] \left [ Y-E(Y) \right ]\right \}$

$D(X),D(Y)$ 为方差， $E(X),E(Y)$ 为期望， $cov(X,Y)$ 就是协方差。相关系数是一个取值范围在-1到1之间的数，如果两个随机变量正相关，那么相关系数为1，如果两个随机变量负相关，那么相关系数为-1，如果两个随机变量不相关，则相关系数为0。

3 算法实现

手写数字识别问题，其实就是通过计算模板图片与待识别样本图片的相关系数问题。对于二维的图片，可以看作是二维的矩阵，其相关系数的计算公式如下：

上式子中， $w(x,y)$ 为模板图片， $f(j,j)$ 为待识别图片， $\bar{w},\bar{f}$ 分别是模板图片和待识别图片的均值。计算图片的相关系数的算法并不复杂，那么该如何进行手写数字的识别呢？

首先，选出一部分手写数字图片作为模板图片，然后用待识别图片跟模板图片逐个进行比对，计算相关系数，然后选出相关系数最大的模板，这个模板所代表的分类，就是待识别图片的分类，算法的流程如下图所示。

上图所示作为例子，每个数字选出一个标准模板，待识别的手写数字为2，通过计算待识别图片与标准模板的相关系数，得到最大的相关系数为0.54，这是待识别数字和模板数字2的相关系数，所以最终的识别结果是2。有时候，还需要评估一下识别的置信度，这就需要通过softmax函数进行归一化，得到分类的置信度，上图的例子的置信度是0.12，并不算高，不过它最大，因此仍然可以作为分类的依据。

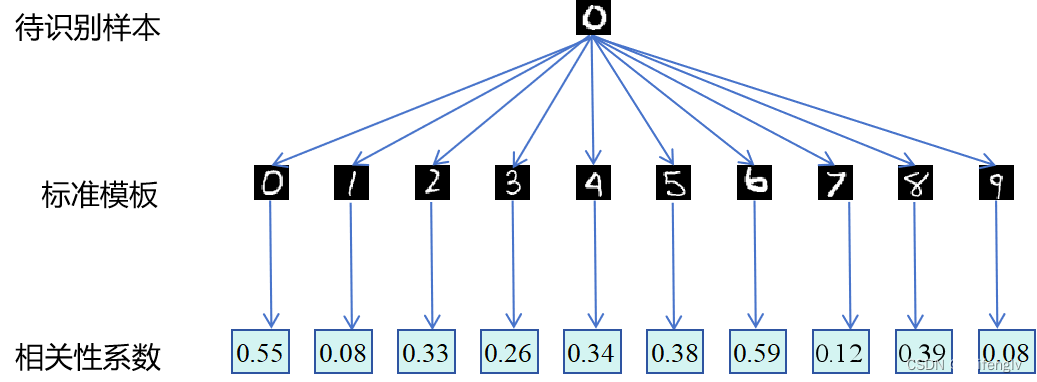
在每一种数字选用一张模板图片的情况下，实验的结果是，识别的精度只有0.45，这只比胡乱蒙的结果好一点。有时候，相关系数不一定正确地表示图片的相似程度，对于人眼来说很显然的事情，机器的眼中却未必如此。如下图所示，数字0的待识别图片，与各数字模板图片之间的相关系数。我们可以发现，待识别的数字0与模板的数字0的相关系数不是最高的，反倒是与模板的数字6相关系数最高，因此该待识别的数字0被错误地识别为数字6。

回到上面按图找人的问题，如果只有一张图，我们有较大几率出现识别错误的情况，但是如果多提供几张不同角度拍摄的照片，是否会对我们正确找到人有帮助呢？答案是肯定的。为了避免单个模板提供的信息不足以完成高精度的识别任务，增加一些辅助的模板数据是必要的。我们可以将每种数字的标准模板数量扩展一些，比如10张、100张、200张。比如，每种数字采用10张模板，那么总的模板数量就有100张。先用待识别数字与数字0的10张模板进行相关系数计算，选出相关系数最大的作为代表数字0的相关系数，然后用待识别数字与数字1的10张模板进行相关系数计算，选出相关系数最大的作为代表数字1的相关系数，依次类推分别计算出0-9个数字的相关系数，然后在根据这10个相关系数进行排序和置信度计算，选出置信度最大的模板，就是待识别数字的最终分类。

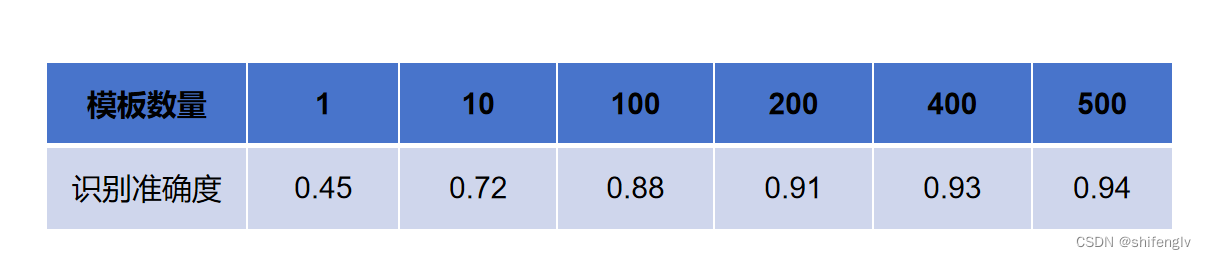
经过实验，当每种数字的模板数量逐步增加，识别的精度也逐步增加。具体的实验结果如下表所示，当模板的数量达到500时，手写数字的识别精度达到了0.94，这个精度比起神经网络算法来说，还是要低一些。但是相对于神经网络，模板匹配不需要大量的样本进行训练。在样本数量较少的情况下，模板匹配算法的性能可能会比神经网络算法好。模板匹配算法，算是一种少样本学习的解决办法。这里模板匹配算法的实现代码和测试数据集，代码是使用python语言实现的，有需要学习的可以下载进行参考。