【因果推断python】53_效应异质性和非线性带来的挑战1

Treatment Effects on Binary Outcomes

合成一些数据

由于缺乏基本事实，在单位层面预测治疗效果极为困难。因为我们只能观察到一个潜在结果 T(t)
，我们无法直接估计它。相反，我们必须依靠目标变换（也可以看作是设计巧妙的损失函数）来估计条件治疗效果，但只能是期望值。但这并不是唯一的挑战。由于治疗效果非常不稳定，其估计值通常会有相当大的噪声。这对于我们想根据治疗效果来划分治疗单位的应用（比如我们想进行个性化治疗分配）来说，会产生巨大的实际影响。

现在我们将看到，有时如果我们不直接估算 CATE，而是关注另一个通常方差较小的替代目标，就能获得更好的治疗效果分割。出现这种情况的常见情况是，所关注的结果变量Y是二元变量。

Treatment Effects on Binary Outcomes

import pandas as pd
import numpy as np
import seaborn as sns
import statsmodels.formula.api as smf
from matplotlib import pyplot as plt
from matplotlib import style
style.use("ggplot")
from typing import List

import numpy as np
import pandas as pd
from toolz import curry, partial

@curry
def avg_treatment_effect(df, treatment, outcome):
    return df.loc[df[treatment] == 1][outcome].mean() - df.loc[df[treatment] == 0][outcome].mean()
    
    

@curry
def cumulative_effect_curve(df: pd.DataFrame,
                            treatment: str,
                            outcome: str,
                            prediction: str,
                            min_rows: int = 30,
                            steps: int = 100,
                            effect_fn = avg_treatment_effect) -> np.ndarray:
    
    size = df.shape[0]
    ordered_df = df.sort_values(prediction, ascending=False).reset_index(drop=True)
    n_rows = list(range(min_rows, size, size // steps)) + [size]
    return np.array([effect_fn(ordered_df.head(rows), treatment, outcome) for rows in n_rows])


@curry
def cumulative_gain_curve(df: pd.DataFrame,
                          treatment: str,
                          outcome: str,
                          prediction: str,
                          min_rows: int = 30,
                          steps: int = 100,
                          effect_fn = avg_treatment_effect) -> np.ndarray:
    

    size = df.shape[0]
    n_rows = list(range(min_rows, size, size // steps)) + [size]

    cum_effect = cumulative_effect_curve(df=df, treatment=treatment, outcome=outcome, prediction=prediction,
                                         min_rows=min_rows, steps=steps, effect_fn=effect_fn)

    return np.array([effect * (rows / size) for rows, effect in zip(n_rows, cum_effect)])

如果你在一家科技公司工作，你可能会遇到一个非常常见的问题：管理层希望通过某种手段提高客户对产品的转化率。例如，他们可能希望通过提供 10 BRL 的优惠券让客户进行应用内购买，从而增加应用的安装数量。或者在您首次使用他们的共享乘车应用时提供免费乘车服务。或者降低投资平台前三个月的交易费用。由于 "怂恿 "往往成本高昂，他们很希望不必为每个人都这样做。相反，如果我们能只对那些最敏感的客户使用促进转换的暗示，那就再好不过了。

从因果推理的角度来看，您现在可能已经知道，这类业务问题属于治疗效果异质性（TEH）范畴。具体来说，你有一个代价高昂的激励作为处理 T，转换为二元结果 Y 以及客户治疗前的具体特征 X
. 然后，您就可以用类似于双重/偏差异质性（Double/Debiased）的方法来估计条件平均治疗效果 $E[Y_1-Y_0|X]$ 然后，您可以使用类似于双重/偏差 ML 的方法来估算条件平均处理效果，最后只对估算出的处理效果最高的客户进行激励。用商业术语来说，这就是个性化转换策略。您将找到转化增量高的客户群，并只对他们使用激励。

然而，这里有一个复杂因素，使得 TEH 方法并不那么明显。事实上，结果是二进制的，这让事情变得相当复杂。因为这有点违背直觉，所以我更愿意先说明发生了什么，然后再解释为什么会发生。

合成一些数据

让我们把这个问题简单化，但仍然可以联系起来。我们将模拟处理方法 "推移"（nudge）是完全随机的，从伯努利（Bernoulli）中抽取，p=0.5. 这意味着治疗是根据一枚公平的硬币分配的。这也意味着我们不需要注意任何混杂因素。

$nudge\sim\mathcal{B}(0.5)$

接下来，让我们按照伽马分布模拟客户的协变量年龄和收入。这些都是您所了解的客户信息，因此，您希望根据这些信息进行个性化定制。换句话说，您希望找到由年龄和收入定义的客户群体，从而使其中一个群体对推理处理反应强烈。

$\begin{aligned}&age\sim G(10,4)\\&income\sim G(20,2)\end{aligned}$

最后，我们将模拟转换。为此，我们将首先创建一个遵循随机噪声线性模型的潜变量。重要的是，请注意收入对 $Y_{latent}$ 有很高的预测性，但它不会改变治疗效果。简单地说，"推导 "对所有收入水平的 $Y_{latent}$ 对所有收入水平的影响都是一样的。与此相反，年龄只通过与推导治疗的交互作用影响 $Y_{latent}$ 的影响。

$Y_{latent}\sim N(-4.5+0.001 income+nudge+0.01 nudge age,1)$

得到 $Y_{latent}$ 值后，我们可以通过设置 $Y_{latent}$ >x 来模拟转换。首先，让我们设置 x=0，这样转化率大致为 50%。也就是说，平均有 50%的客户转化为我们的产品。

$conversion=1\{Y_{latent}>0\}$

np.random.seed(123)

n = 100000
nudge = np.random.binomial(1, 0.5, n)
age = np.random.gamma(10, 4, n)
estimated_income = np.random.gamma(20, 2, n)*100

latent_outcome = np.random.normal(-4.5 + estimated_income*0.001 + nudge + nudge*age*0.01)
conversion = (latent_outcome > .1).astype(int)

为了方便起见，我们还可以将所有内容存储在 DataFrame 中。另外，检查一下平均转换率是否接近 50%。

df = pd.DataFrame(dict(conversion=conversion,
                       nudge=nudge,
                       age=age,
                       estimated_income=estimated_income,
                       latent_outcome=latent_outcome))

df.mean()

至于平均治疗效果，由于治疗是随机进行的，我们可以用治疗组和对照组平均值的简单差值来估算： $E[Y|T=1]-E[Y|T=0]$ . 那么，让我们来看看这些治疗平均值是什么样的。我们将从潜在结果和转换角度来研究它们。这里有一点很重要。

df.groupby("nudge")[["latent_outcome", "conversion"]].mean()

avg_treatment_effect(df, "nudge", "latent_outcome")
1.4023163965477656
avg_treatment_effect(df, "nudge", "conversion")
0.39477273768476406

潜在结果的 ATE 非常简单。根据我们的数据生成模型，我们知道这一效应应为 1 + avg（年龄）*0.01。由于平均年龄约为 40 岁，因此 ATE 约为 1.4。更有趣（也更复杂）的地方在于转换的 ATE。由于转换的界限在 0 和 1 之间，因此其 ATE 不会是线性的。因此，我们无法像处理潜在结果那样，通过一个简单的公式来推导它（有一个公式，但相当复杂）。我们只能说影响较小。这有道理吧？我的意思是，治疗不可能使转化率提高 1.4 个百分点，因为转化率不可能超过 100%。现在，我要你们牢牢记住这个事实，因为它对我们理解接下来的内容至关重要。

现在让我们来谈谈条件平均治疗效果（CATE）。纵观我们的数据生成过程，我们知道一个事实，即估计收入会预测转化率，但不会改变激励对转化率的影响。因此，根据估计收入对客户进行细分将产生具有相同处理效果的细分。相比之下，年龄只会通过与诱导的交互作用影响转化率。因此，不同年龄的细分市场对治疗的反应会截然不同，而不同收入的细分市场则不会。换句话说，估计收入不应该是一个好的个性化变量，而年龄应该是。

通过累积效应曲线可以看出这一点。年龄的曲线应该从离 ATE 很远的地方开始，然后慢慢向 ATE 靠拢，而估计收入的曲线应该只在 ATE 附近波动。这正是我们在绘制对潜在结果的推移效应的累积效应曲线时所看到的。

cumulative_effect_fn = cumulative_effect_curve(df, "nudge", "latent_outcome", min_rows=500)

age_cumm_effect_latent = cumulative_effect_fn(prediction="age")
inc_cumm_effect_latent = cumulative_effect_fn(prediction="estimated_income")

plt.plot(age_cumm_effect_latent, label="age")
plt.plot(inc_cumm_effect_latent, label="est. income")
plt.legend()
plt.xlabel("Percentile")
plt.ylabel("Effect on Latet Outcome");

同样，潜在结果也非常好。由于它的线性，我们的预期与现实非常吻合。但在现实生活中，我们并不关心（也没有）潜在结果。我们有的只是转换。在转换过程中，事情看起来要复杂得多。如果我们绘制累积效应曲线，年龄仍然显示出一定的治疗效果异质性，从 ATE 以上开始，慢慢向 ATE 靠拢。这意味着年龄越大，治疗效果越高。到目前为止还不错。这正是我们所期望的。

cumulative_effect_fn = cumulative_effect_curve(df, "nudge", "conversion", min_rows=500)

age_cumm_effect_latent = cumulative_effect_fn(prediction="age")
inc_cumm_effect_latent = cumulative_effect_fn(prediction="estimated_income")

plt.plot(age_cumm_effect_latent, label="age")
plt.plot(inc_cumm_effect_latent, label="est. income")
plt.legend()
plt.xlabel("Percentile")
plt.ylabel("Effect on Conversino");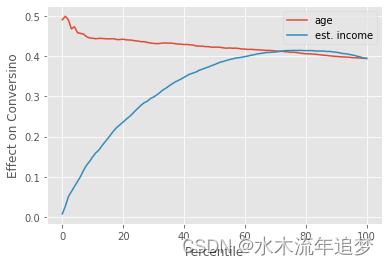

然而，根据估计收入的不同，治疗效果也存在很大的异质性。估计收入较高的客户的治疗效果要低得多，这导致累积效果曲线在开始时一直趋于零，然后慢慢向 ATE 收敛。这就告诉我们，就个性化而言，估计收入将产生比年龄产生的细分市场具有更多治疗效果异质性（TEH）的细分市场。

这很不方便吧？为什么我们知道年龄这一特征会导致治疗效果异质性，但与我们知道不会改变治疗效果的特征（估计收入）相比，年龄这一特征却更不利于个性化呢？答案就在于结果函数的非线性。虽然估计收入不会改变激励对潜在结果的影响，但一旦我们将该潜在结果转换为转换（至少是间接转换），它就会改变。转换不是线性的。这意味着它的导数会根据你所处的位置而变化。由于转换率最高只能达到 1，如果转换率已经很高，就很难再提高。换句话说，高转换率的导数非常低。但是，由于转换率也以 0 为界，如果转换率已经很低，导数也会很低。转换率呈 S 型，两端的导数都很低。我们可以通过绘制按估计收入分段（100 乘以 100 的分段）计算的平均转换率来了解这一点。

(df
 .assign(estimated_income_bins=(df["estimated_income"]/100).astype(int)*100)
 .groupby("estimated_income_bins")
 [["conversion"]]
 .mean()
 .plot()
);

请注意，当转换率非常高时，这条曲线的斜率（导数）非常小。当转换率很低时，斜率（导数）也很小（不过由于该地区样本较少，这一点比较难看出来）。有了这些信息，我们就可以解释为什么 estimated_income 会产生具有高度治疗效果异质性的区段。

由于 "估计收入 "对转换具有很高的预测性，我们可以说，"估计收入 "不同的客户属于 S 型转换曲线的不同位置。估计收入非常高或非常低的客户位于曲线的两端，导数较低，这意味着提高转换率的难度更大，进而意味着治疗效果可能较小。另一方面，报告收入在中间范围的客户也位于转换曲线的中间，导数较高，因此治疗效果也可能较高。我之所以说 "可能"，是因为从理论上讲，一个变量有可能具有很强的效果修正力，以至于在我们穿越转换曲线时，它主导了导数的变化。然而，至少从我的经验来看，S 型转换曲线的曲率往往会主导我们的其他所有效应修正。

不过，这并不只是我一个人的看法。这是我从苏珊-阿特伊斯（Susan Atheys）在哥伦比亚数据科学研究所的演讲中获得的一张幻灯片。在这里，她讨论的是让学生申请联邦财政援助以支付大学学费的激励效果。这也是一个转换问题。她发现，最好的策略是针对那些已经有可能转化的学生。她还说，针对那些转化可能性低的学生是个坏主意

等一下但这不是你第一次说的话！你说，无论是很高的转化率还是很低的转化率，其衍生率都很低，因此治疗效果也很低！

嗯，这是正确的。然而，在现实生活中，转换率很少会挤满整个 S 型曲线。我们通常看到的是，每个人都挤在曲线的一端或另一端。就商业而言，你的平均转化率很少达到 50%。更常见的是 70% 到 90% 或者 1% 到 20%。在这些更有可能的情况下，针对那些基线较高的人可能是一个好主意，也可能是一个坏主意。

我的意思是这样的：让我们使用之前的潜在结果，但现在通过将其设置为 latent_outcome > 2，生成一种平均转化率较低的情况。接下来，让我们通过设置 latent_outcome > -2 来生成一种转换率高的情况。

df["conversion_low"] = conversion = (latent_outcome > 2).astype(int)
df["conversion_high"] = conversion = (latent_outcome > -2).astype(int)

print("Avg. Low Conversion: ", df["conversion_low"].mean())
print("Avg. High Conversion: ", df["conversion_high"].mean())
Avg. Low Conversion:  0.12119
Avg. High Conversion:  0.9275

根据我们对转化率非线性的了解，我们已经可以预测会发生什么。在低转化率的情况下，针对高基线转化率（高估计收入）的目标群体会更有效。这是因为我们处于 S 型转换曲线的左侧，基线转换率越低，导数就越小。在这一区域，高基线转换率将转化为高治疗效果。因此，我们应该对基线转换率高的人群，也就是估计收入较高的人群进行干预。

cumulative_effect_fn = cumulative_effect_curve(df, "nudge", "conversion_low", min_rows=500)

age_cumm_effect_latent = cumulative_effect_fn(prediction="age")
inc_cumm_effect_latent = cumulative_effect_fn(prediction="estimated_income")

plt.plot(age_cumm_effect_latent, label="age")
plt.plot(inc_cumm_effect_latent, label="est. income")
plt.xlabel("Percentile")
plt.ylabel("Effect on Conversino");
plt.legend();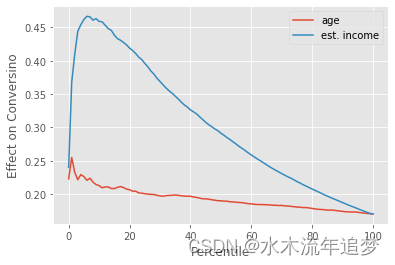

就像我们预测的那样，估计收入高的人，也就是基线转换率高的人，治疗效果要高得多。

现在，对于转换率高的另一种情况，平均而言，基线转换率高的人的治疗效果会较低。因此，以估计收入高的人群为目标并不是一个好主意。我们可以从倒置的累积效应曲线看出这一点，即估计收入高的人的治疗效果较低。

cumulative_effect_fn = cumulative_effect_curve(df, "nudge", "conversion_high", min_rows=500)

age_cumm_effect_latent = cumulative_effect_fn(prediction="age")
inc_cumm_effect_latent = cumulative_effect_fn(prediction="estimated_income")

plt.plot(age_cumm_effect_latent, label="age")
plt.plot(inc_cumm_effect_latent, label="est. income")
plt.xlabel("Percentile")
plt.ylabel("Effect on Conversino")
plt.legend();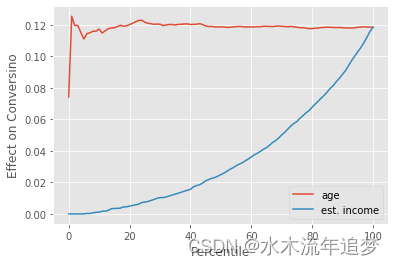

总之，我们看到的是，当结果是二元时，治疗效果往往受 Logistic 函数的曲率（导数）支配。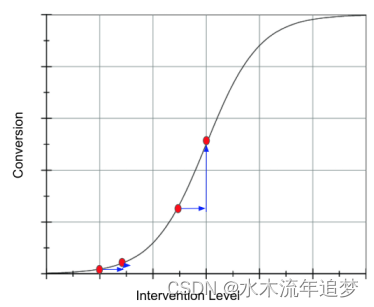

例如，在我们的转化问题中，如果平均转化率较低，我们就会处于逻辑曲线的左侧，在高基线转化率的情况下，治疗效果会更高。这将转化为一种激励政策，主张对转化概率已经很高的客户进行治疗（激励）。另一方面，如果平均转化率较高，我们就会处于逻辑曲线的右侧，基线转化率较低的客户的导数（以及治疗效果）会更高。

这当然需要记住很多东西，但我们完全可以简化：只要谁的基线转换率更接近 50%，就对谁进行治疗。这里的数学论证非常可靠：逻辑导数的峰值是 50%，因此只需处理更接近这一点的单位。

更妙的是，这是少有的常识与数学相符的情况。在市场营销中，这些转换问题非常常见，有一种观点认为，我们不应该针对输掉的赌注（转换概率非常低的赌注），也不应该针对稳赢的赌注（转换概率非常高的赌注）。相反，我们应该瞄准那些处于中间位置的人。这一点非常吸引人，因为这与我们使用更正式的因果论证所得出的结论完全相同。