多年来,数据一直是世界运作的重要组成部分。这些数据可以从GDP到血样,再到世界的各个方面。随着我们数据的增长,统计学找到了从它们中提取更多意义的方法。
这些方法之一被称为方差分析(ANOVA)。方差分析是一套统计模型,分析平均值之间的差异。微软在Excel中提出了统计学插件来解决这些问题。然而,微软的Excel仍然有一定的局限性。后来又出现了R-studio和Python等工具。
有了Python,对正态性和同质性的检验变得更加容易。本教程的重点是用Microsoft Excel创建一个方差分析表,用箱形图测试单程方差分析的正态性,以及用Python测试同质性的Bartlett规则。
前提条件
本教程要求读者具备以下方面的适当知识。
- 方差分析(ANOVA)。
- [Microsoft Excel]。
- [Python]。
目标
在本教程结束时,读者将能够。
- 使用Excel创建一个方差分析表。
- 安装必要的Python依赖,以创建一个箱形图。
- 使用箱形图测试正态性。
- 使用Bartlett规则测试同质性。
设置环境
我们需要安装Python和它的一些依赖项来开始工作。
我们需要安装以下依赖项。
- pandas
- matplotlib
- seaborn
安装pandas、matplotlib、seaborn
有几种方法来安装Python依赖项,最流行的是使用软件包管理器,如pip或conda。
要安装pandas ,我们需要。
- 打开我们的终端(无论是我们IDE的终端还是命令提示符)。
注意:如果你使用的是命令提示符,确保将默认文件夹添加到PATH中。
- 键入以下命令。
python -m pip install pandas
复制代码稍等片刻,直到依赖关系安装完毕。接下来,我们将分别使用下面的命令对其他依赖项采取同样的步骤。
python -m pip install matplotlib
复制代码python -m pip install seaborn
复制代码安装完这些依赖项后,我们将用Excel创建一个方差分析表。
开始吧
用Excel创建一个方差分析表
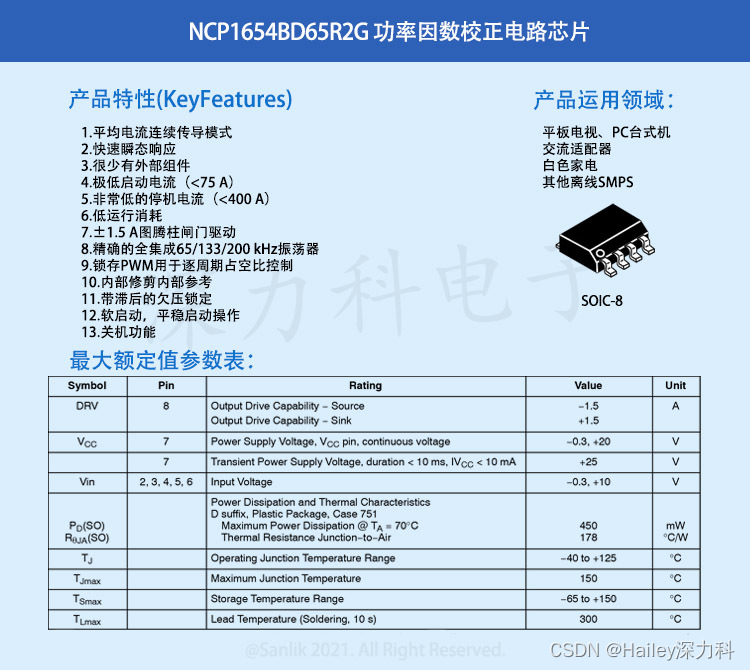
Microsoft Excels的Analysis Toolpak插件是统计分析领域的一个变革者。我们将向你展示如何创建一个包含平方和、自由度、平均平方、F值、P值、F临界值的方差分析表。
要进行单因素方差分析,请执行以下步骤。
- 以任何首选的Excel格式导入你的数据集。
 进入 "数据 "标签,点击 "数据分析 "子标签。如果你找不到这个子标签,请检查下面的小标题。
进入 "数据 "标签,点击 "数据分析 "子标签。如果你找不到这个子标签,请检查下面的小标题。- 选择方差分析:单因素,然后点击确定。
- 点击输入范围,突出显示你要使用的数据集。
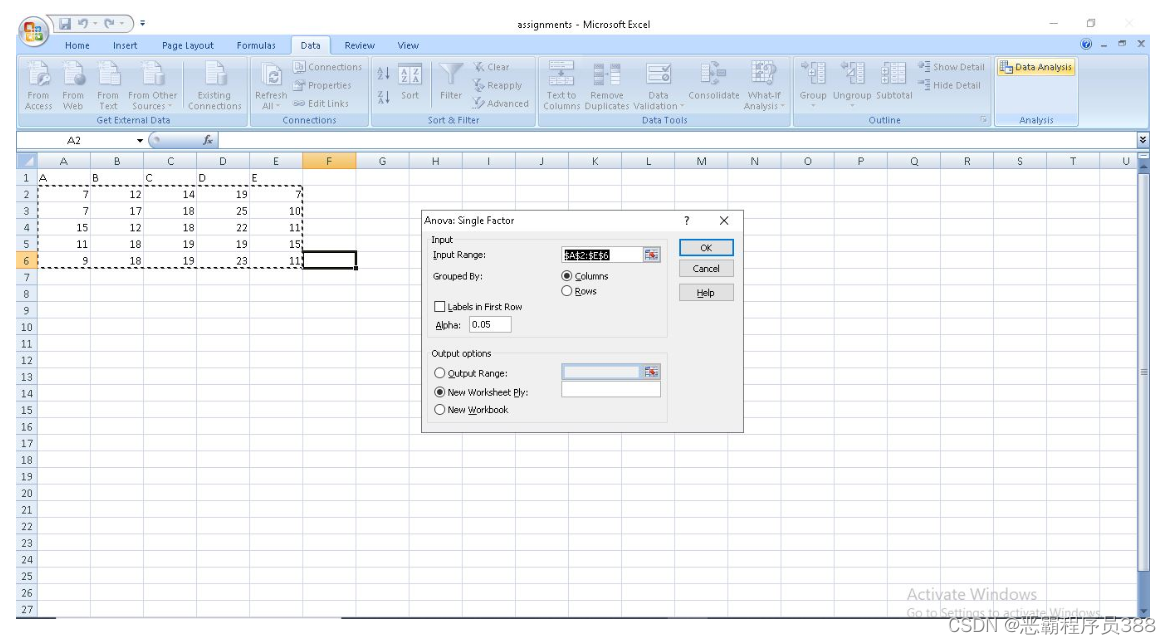
注意:单独突出显示数据集中的数字。
- 你可以决定是否要在同一个电子表格或另一个电子表格中查看。
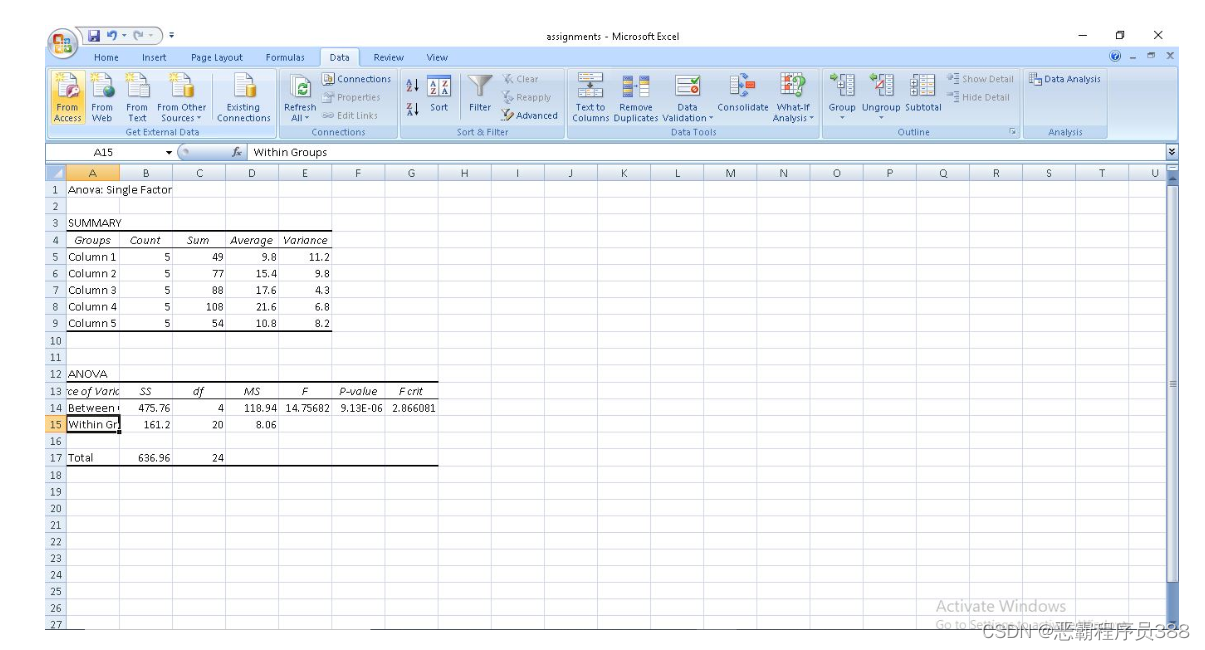
在我们上面的方差分析表中,我们分析了方差分析的平方和和其他值。有了这个,我们就可以用Microsoft Excel解决单因子方差分析。
分析工具箱
对于我们要做的事情,分析工具箱是一个必不可少的插件。为了加载这个插件,我们要做以下工作。
- 点击文件按钮或左上角的微软标志。
- 选择Excel选项,向下滚动到加载项。
- 在列表中,选择Analysis Toolpak并点击
Go。 - 勾选Analysis Toolpak并选择
Ok。 - 回到数据标签,你会注意到数据分析子标签。
使用箱形图测试正态性
我们将创建一个Python文件并将Pandas、Matplotlib和Seaborn导入我们的代码中。Pandas, Matplotlib & Seaborn是用于数据分析的Python库。
这些库在数据可视化中非常重要。Pandas导入了大量的数据格式,而Matplotlib和Seaborn是可视化库,用于生成强大的可视化数据。Seaborn是一个用Python编译统计图形的库。
接下来,我们将使用pandas库中的read() 方法读取我们的数据集(我们使用CSV文件格式)。我们将使用melt() 方法重塑适合统计模型包的数据框架,并在下面一行中替换来自pandas库的列名。
然后,我们将生成一个boxplot,使用我们的seaborn工具和plt.show() 函数来显示我们的箱形图,以查看各治疗的数据分布。
注意:当从目录中读取时,请使用双反斜杠或将
r放在目录地址的前面,用引号包裹。

下面是上述说明的一个实现。
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
data_set = pd.read_csv(r"C:\Users\DELL\Desktop\one-way-anova-excel-testing-normality-homogeneity-using-python\assignments.csv")
data_set_melt = pd.melt(data_set.reset_index(), id_vars=['index'], value_vars=['A', 'B', 'C', 'D', 'E'])
data_set_melt.columns = ['index', 'treatments', 'value']
ax = sns.boxplot(x='treatments', y='value', data=data_set_melt, color='#99c2a2')
ax = sns.swarmplot(x="treatments", y="value", data=data_set_melt, color='#7d0013')
plt.show()
复制代码在实现上,图示如下。
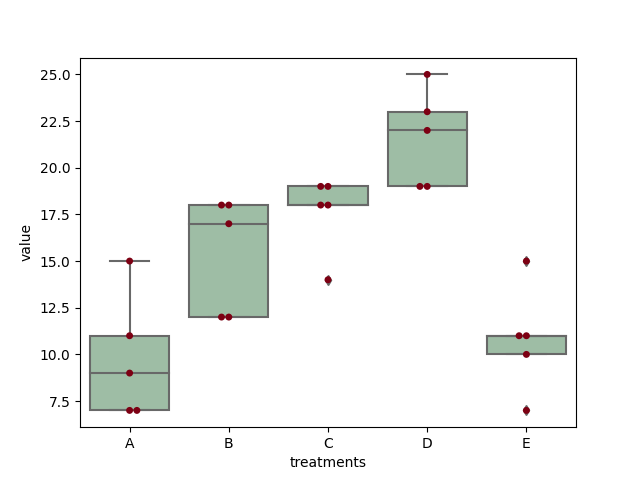
使用巴特利特规则测试同质性
在展示相关过程之前,我们先谈一谈这个规则。Maurice Stevenson Bartlett发明了这一规则。它是一个用来检查从不同人群中抽取的样本是否具有相同变异的程序。
它检验的假设是,各组的差异是相等的。这种检验的常规结构包括
- 建立一个假设(无效假设和备用假设)。
- 计算检验统计量。
- 寻找临界值。
- 得出结论。
好消息!Python 已经将这些过程编译成一行短短的代码。为了做到这一点,我们将导入scipy.stats 并在我们的数据集上调用 Bartlett 的方法。
例子
A = 7,12,14,19,7
B = 7,17,18,25,10
C = 15,12,18,22,11
D = 11,18,19,19,15
E = 9,18,19,23,11
import scipy.stats as stats
print(stats.bartlett(A, B, C, D, E))
复制代码当我们在终端上运行上面的代码时,我们应该得到。

结论
我们可以使用Python在方差分析中进行几种正态性和同质性的测试。在这篇文章中,我们已经学会了如何用箱形图测试正态性和用Bartlett规则测试同质性。